Оригинал статьи: Ранговый анализ и ансамблевая модель машинного обучения для прогнозирования нагрузок в узлах центральной энергосистемы Монголии
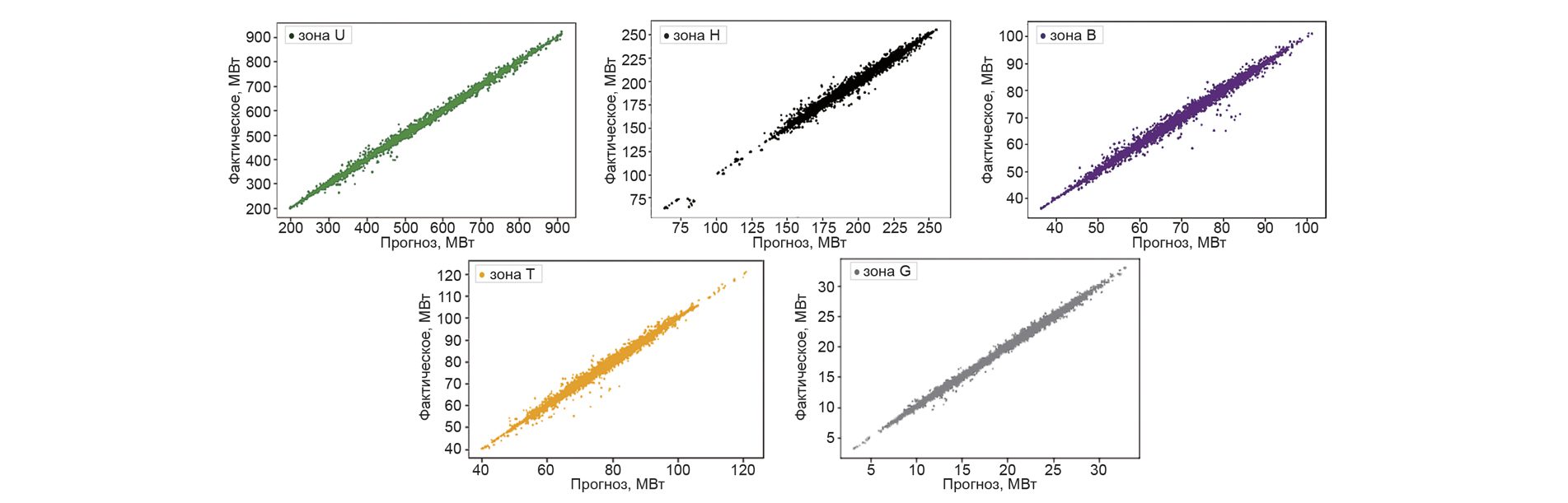
Электроэнергетическая система представляет собой сложный объект, включающий большое количество структурных элементов, связанных иерархически. Задача моделирования ее структуры и прогнозирования процессов, происходящих в ней как в целом, так и в ее элементах, является ключевым вопросом управления режимами работы энергосистемы. В работе использовался метод машинного обучения, основанный на алгоритме случайного леса (Random Forest) для построения суточного графика нагрузки, и применялись ранговые коэффициенты для моделирования потребления в узлах. Выполнена программная реализация с помощью языка программирования Python. Результаты данной работы показали, что потребление в любых узлах энергосистемы возможно определять ранговыми коэффициентами.