Расчет распределительной сети на основе трехфазных схем замещения

Оригинал статьи: Расчет распределительной сети на основе трехфазных схем замещения

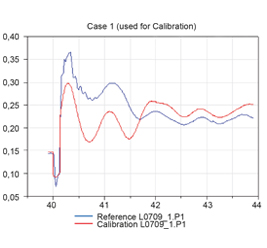
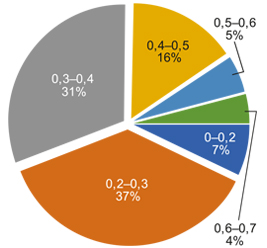
Ключевые слова: распределительная сеть, схема замещения, оборудование распределительной электрической сети

Читать онлайн

Предложена методика расчета параметров распределительной электрической сети 0,4 кВ на основе трехфазных схем замещения. Показаны преимущества моделирования трехфазных схем замещения распределительных электрических сетей перед моделированием на основе однофазных схем замещения.