Выбор методики определения сработанного ресурса современных кабельных линий

Page 1

Page 2

«КАБЕЛЬ-news», № 1, 2014, www.kabel-news.ru

Актуально

ÐÅÑÓÐÑ ÊÀÁÅËÜÍÛÕ ËÈÍÈÉ

ысоковольтные кабельные линии (КЛ) при
эксплуатации подвергаются воздействию
перенапряжений, повышенных темпера-
тур, влажности, механических нагрузок и

т.д. Эти воздействия приводят к старению электри-
ческой изоляции, к пробоям и выходу из строя КЛ.
Поэтому с учётом всё возрастающих требований к
бесперебойному электроснабжению потребителей
актуальной задачей является выбор расчётных ме-
тодов достоверного определения сработанного ре-
сурса КЛ с учётом действия эксплуатационных фак-
торов.

Известным подходом при оценке ресурса явля-

ется установление взаимосвязи между величиной
среднего ресурса и воздействующими на изоляцию
КЛ эксплуатационными факторами. Эта взаимо-
связь рассмотрена на примере модели, предложен-
ной в [1]. Определение фактического сработанного
ресурса R в зависимости от изменения величины
воздействующих факторов Х

выполняется по выра-

жению:

(1),

где i = 1…N — количество эксплуатационных

факторов, оказывающих воздействие на сработку
ресурса, Х

— отклонение i-го фактора от норма-

тивного значения Х

В настоящее время широкое применение полу-

чили силовые кабели с поливинилхлоридной (ПВХ)
изоляцией и с изоляцией из сшитого полиэтилена
(СПЭ). Так как КЛ служат на объектах энергетики

для передачи электроэнергии от источника питания
к потребителю, то целесообразно выбрать времен-
ные единицы измерения наработки.

Силовые кабели подвергаются воздействию раз-

личных групп эксплуатационных факторов: химиче-
ских, электрических, механических, температурных.

Оценка влияния химических факторов на жилы ка-

беля и изоляцию может быть произведена, как это по-
казано в [1].

Действие электрических факторов связано

с воздействием напряжённости электрического
поля, которое наблюдается в том числе при ком-
мутационных и грозовых перенапряжениях. Одна-
ко кабели защищаются обычно ограничителями
перенапряжений. Также токи короткого замыкания
создают электродинамические усилия, что может
вызвать механические повреждения изоляции ка-
беля. При выборе кабелей обычно производится
проверка по электродинамической стойкости, по
результатам которой выбирается тип кабеля и спо-
соб его прокладки, который выдержит ударный
ток короткого замыкания на данном участке сети.
В нормативно-технической документации не огова-
риваются сроки службы кабелей при возникновении
в них известных по величине механических напря-
жений. Кроме того, силовые КЛ, особенно при про-
кладке в земле, представляют собой достаточно
надёжную конструкцию против воздействия таких
динамических перегрузок [2]. Поэтому влияние пе-
ренапряжений и электродинамических воздействий
в дальнейшем учитывать не будем.

Согласно [3, 4, 5] ресурс изоляции силовых

Выбор методики
определения сработанного
ресурса современных
кабельных линий

Александр НАЗАРЫЧЕВ, ректор ФГАОУ ДПО

«Петербургский энергетический институт

повышения квалификации» Минэнерго России, д.т.н., профессор,

Дмитрий АНДРЕЕВ, главный специалист ОАО «Зарубежэнергопроект», к.т.н.

Page 3

«КАБЕЛЬ-news», № 1, 2014, www.kabel-news.ru

Актуально

ÐÅÑÓÐÑ ÊÀÁÅËÜÍÛÕ ËÈÍÈÉ

КЛ определяется тепловыми режимами их работы,
которые, в свою очередь, зависят от типа кабеля, ус-
ловий прокладки, температуры окружающей среды,
а также от значения протекающего электрического
тока. В [5] утверждается, что при нагреве жил кабе-
ля до температуры 350

С для кабелей неброниро-

ванных с бумажной пропитанной или пластмассовой
изоляцией и до 400

С для бронированных кабелей с

бумажной изоляцией не происходит разрыва оболо-
чек и повреждения концевых заделок, а также воз-
горания кабелей. Кроме того, в [5] рекомендуется
выполнять расчёт температуры кабелей после каж-
дого воздействия тока короткого замыкания и опре-
делять их пригодность к дальнейшей эксплуатации
при температуре нагрева жил кабелей:
• с пропитанной бумажной изоляцией свыше 200

С,

но не более 300

С;

• с полимерной изоляцией свыше 160

С, но не бо-

лее 250

С.

Допускается временное сохранение в эксплуа-

тации этих кабелей до их замены в течение 1 года.
Такие кабели после воздействия тока короткого за-
мыкания должны быть осмотрены, концевые задел-
ки при необходимости отремонтированы, а также
должны быть проведены испытания повышенным
напряжением. При температуре нагрева жил кабе-
лей выше указанных значений кабели считаются не-
пригодными к дальнейшей эксплуатации и подлежат
немедленной замене.

Анализируя каталоги силовых кабелей с ПВХ-

изоляцией и изоляцией из СПЭ различных заводов-
изготовителей, были установлены следующие
предельно допустимые температуры нагрева:
160

С — для кабелей с ПВХ-изоляцией сечением

меньшим или равным 300 мм

; 140

С — для кабелей

с ПВХ-изоляцией сечением более 300 мм

; 250

С —

для кабелей с изоляцией из СПЭ.

Таким образом, при воздействии токов коротко-

го замыкания определённой величины и продолжи-
тельности остаточный срок службы кабелей равен
1 году при любых дальнейших режимах работы, при
которых температура нагрева жил превышает сле-
дующие значения для:
• кабелей с ПВХ-изоляцией сечением меньшим

или равным 300 мм

— до



доп

= 160

С;



кабелей с ПВХ-изоляцией сечением более
300 мм

— до



доп

= 140

С;



кабелей с изоляцией из СПЭ любого сечения —
до



доп

= 250

С;

• кабелей с пропитанной бумажной изоляцией —

до



доп

= 200—300

С.

Очевидно, что все ограничения по срокам служ-

бы КЛ связаны с процессами нагрева кабелей. Ни-
каких ограничений на длительность коротких за-
мыканий в [5] не накладывается. Однако учитывая,

что, например, для кабелей в системе собственных
нужд электростанций максимальная расчётная дли-
тельность короткого замыкания составляет 4 с, в [5]
приведена номограмма для определения конечной
температуры кабеля при коротком замыкании. Так
как ограничения связаны лишь с температурами на-
грева кабелей, то, очевидно, их можно использовать
при любых режимах работы кабеля, в которых про-
исходит нагрев до указанных выше температур.

В [6, 7] предлагается определять фактический

срок службы кабелей в зависимости от температуры
по



-градусному правилу и закону Вант-Гоффа —

Аррениуса. Согласно [7] нормативный ресурс сило-
вых кабелей составляет R

=25 лет. При этом по дан-

ным каталогов принимается:
• для кабелей с ПВХ-изоляцией



= 70

С;

• для кабелей с изоляцией из СПЭ



= 90

С;

• для кабелей с пропитанной бумажной изоляцией



= 60 или 65

С [7].

Значения



для отдельных типов кабелей могут

несколько отличаться от приведённых и должны ука-
зываться производителями в нормативной докумен-
тации или в технических условиях на эксплуатацию
таких КЛ.

По принятой сегодня терминологии остаточный

срок службы соответствует нормативному оста-
точному ресурсу R

0.ост.

Так как в [5] не указано, при

каких нагрузках кабель после короткого замыка-
ния и нагрева до оговорённых выше температур
проработает ещё 1 год до замены, то примем этот
режим, соответствующий нормативному режиму
работы.

Учитывая всё вышесказанное, можно сделать

вывод о том, что силовой кабель за время работы в
ненормативных условиях R

, которые привели к его

нагреву до указанных выше температур



доп

, сраба-

тывает фактический ресурс в объёме R

-1 год, кото-

рый в именованных единицах можно записать сле-
дующим образом:

(2)

или

(3).

Выразим из формул (2) и (3) величины



и по-

лучим соответственно:

(4),

(5).

Приняв в формулах (4) и (5) R

= 25 лет,



= {60;

65; 70; 90}

C и



доп

= {140; 160; 200; 250; 300}

C в

зависимости от типа кабеля, можно рассчитать со-

Page 4

«КАБЕЛЬ-news», № 1, 2014, www.kabel-news.ru

ответствующие величины



. При этом важно от-

метить, что величина R

должна быть такова, чтобы

за это время кабель данного типа и сечения (мм

)

нагрелся от температуры



до



доп

. Уравнение на-

грева кабеля до температуры



уст

выражается за-

висимостью [9]:

(6),

где



уст

— установившаяся температура; R

— вре-

мя нагрева; T — постоянная времени при известных
условиях прокладки кабеля.

С учётом выражения (6) кривая нагрева кабеля от

начальной температуры



до температуры



доп

описывается формулой:

(7).

Температура



доп

является абстрактной границей

сработки кабелем фактического ресурса, равного
(R

- 1), за время R

нагрева до этой температуры.

Если кабель за время R

не нагрелся до температуры



доп

, то фактический сработанный ресурс не опреде-

лён, а если нагрелся, то определён и равен (R

- 1) [5].

При применении экспоненциального закона процесс
можно считать установившимся уже после истечения
времени, равного R

= 4T, при этом погрешность при

определении температуры составит 1%. Таким обра-
зом, величина R

= 4T характеризует максимальное

время, за которое кабель нагрелся до температу-
ры



доп

, определённой с абсолютной погрешностью

~0,01



доп

. Это возможно при нормальных и перегру-

зочных режимах работы кабеля, когда релейная за-
щита не срабатывает и при данном токе кабель про-
должает постепенно нагреваться до определённой
установившейся температуры. С учётом этого выра-
жения (4) и (5) примут соответственно вид:

(8),

(9).

Из формул (8) и (9) очевидно, что величины



зависят лишь от типа кабеля и условий его

прокладки, так как параметры



доп

, R

зависят от

типа кабеля, а величина T — от типа и условий про-
кладки. Подставим (8) и (9) соответственно в (2) и
(3), с учётом (1) получим в именованных единицах
значения фактического сработанного ресурса КЛ:

(10),

(11).

При использовании выражений (10) и (11) не-

обходимо иметь в виду, что в (10) температура мо-
жет измеряться как по Цельсию, так и по Кельвину.
В выражении (11) — только по шкале Кельвина.
Фактическую установившуюся температуру кабеля
можно определить по хорошо известной методике,
изложенной, например, в [8]. При прокладке в возду-
хе величина постоянной времени Т = Т

может быть

вычислена так [9]:

= (S

+ S

)[с

+ 0,5(с

из

+ с

об

)]

(12),

где S

— тепловое сопротивление изоляции кабеля;

— тепловое сопротивление поверхности кабеля;

, с

из

, с

об

— удельные теплоёмкости жилы, изоляции

и оболочки кабеля.

При прокладке в земле постоянная времени

Т = Т

может быть вычислена по выражению [9]:

= (S

+ S

)[с

+ 0,5(с

из

+ с

об

покр

)] (13),

где S

— тепловое сопротивление защитных покро-

вов кабелей, прокладываемых в земле; S

— тепло-

вое сопротивление почвы; c

покр

— удельная теплоём-

кость защитных покровов кабеля.

В исследованиях [8, 9] для различных кабелей

приводятся все необходимые расчётные формулы
для определения величин S

, S

, а также спра-

вочные данные по значениям величин c

, с

из

, с

об

, c

покр

При коротких замыканиях время нагрева кабе-

ля ограничивается действием релейной защиты.
Например, для кабелей, эксплуатируемых в систе-
ме собственных нужд электростанций, расчёт на
невозгораемость производится с учётом времени
действия резервной релейной защиты, равного 4 с.
В этом случае для определения конечной температу-
ры жилы кабеля



можно воспользоваться следую-

щей формулой [5]:



+ а(е

- 1) (14),

где



— начальная температура жилы кабеля; a =

228

C — величина, обратная температурному коэф-

фициенту электрического сопротивления при 0

С;

k определяется по выражению

k = b ( l

)/S

(15),

где b = 45,65 мм

/(кА

·с) для алюминия; b = 19,58 мм

(кА

·с) для меди; S — поперечное сечение кабеля

(мм

); I — действующее значение тока; R

— длитель-

ность воздействия тока I.

Величина k также может быть определена из вы-

ражения (14) при



доп



доп



+ ае

- а



= (



доп

+ а)/(



+ а), k =

ln [(



доп

+ а)/(



+ а)] (16).

Подставляя a = 228



= {60; 65; 70; 90}

C и



доп

{140; 160; 200; 250; 300}

C для различных типов кабе-

Актуально

ÐÅÑÓÐÑ ÊÀÁÅËÜÍÛÕ ËÈÍÈÉ

Page 5

«КАБЕЛЬ-news», № 1, 2014, www.kabel-news.ru

(28),

(29).

Рассмотрим примеры по определению фактического

сработанного и остаточного ресурса силовых кабелей.

Пример 1

Одножильный алюминиевый кабель с

ПВХ-изоляцией сечением 1х120 мм

, работающий в ста-

ционарном режиме на воздухе. Согласно [9] тепловое
сопротивление изоляции такого кабеля определяется
по выражению: S

= 0,037



lg(R

) = 0,037·650lg(10/6,18) =

5,027

С·см/Вт (30),

где



— удельное тепловое сопротивление изоляции ка-

беля (согласно [9] принимается равным 600—700

С·см/Вт,

в нашем случае — 650

С·см/Вт); R

— внешний радиус

кабеля (для данного кабеля принимается равным



20/2

=10 мм); r

— радиус жилы кабеля (принимаем равным



—



—

= 6,18 мм).

Тепловое сопротивление поверхности кабеля при

прокладке в воздухе определяется по выражению [9]:





= 1000/20



= 15,915

С·см/Вт (31),

где



— удельное тепловое сопротивление поверхно-

сти данного кабеля при прокладке в воздухе (согласно
[9] принимается равным 800—1200

С·см/Вт, возьмём

1000

С·см/Вт); D

— внешний диаметр кабеля (принима-

ем равным



20 мм).

По формуле (12) определим постоянную време-

ни нагрева кабеля: Т

= (S

+ S

)[c

+ 0,5(с

из

+ с

об

)] =

(5,027 + 15,915)[8,89 + 0,5(1,3 + 1,3)] = 240,624 с, где c

8,89 г/см

; с

из

= с

об

= 1,3 г/см

[9].

Допустим, нормативный срок службы данного кабе-

ля составляет R

= 20 лет. Для кабелей с ПВХ-изоляцией

Актуально

ÐÅÑÓÐÑ ÊÀÁÅËÜÍÛÕ ËÈÍÈÉ

лей, можно получить значения коэффициента k. При-
равнивая формулы (15) и (16), найдём величину R

b·(l

)/S

= ln(



доп

+ а)/(



+ а), R

(1/l

)·

/b) ln(



доп

+ а)/(



+ а) (17).

Найдём значения (



) и (1/



- 1/



) по выра-

жениям:



+ а(е

- 1)



= (



доп

+ а)(е

- 1), (18),

(19).

При



доп

после подстановки формул

(18) и (19) соответственно в (4) и (5) получим:

(20),

(21),

где коэффициент k вычисляется по выражению (15).

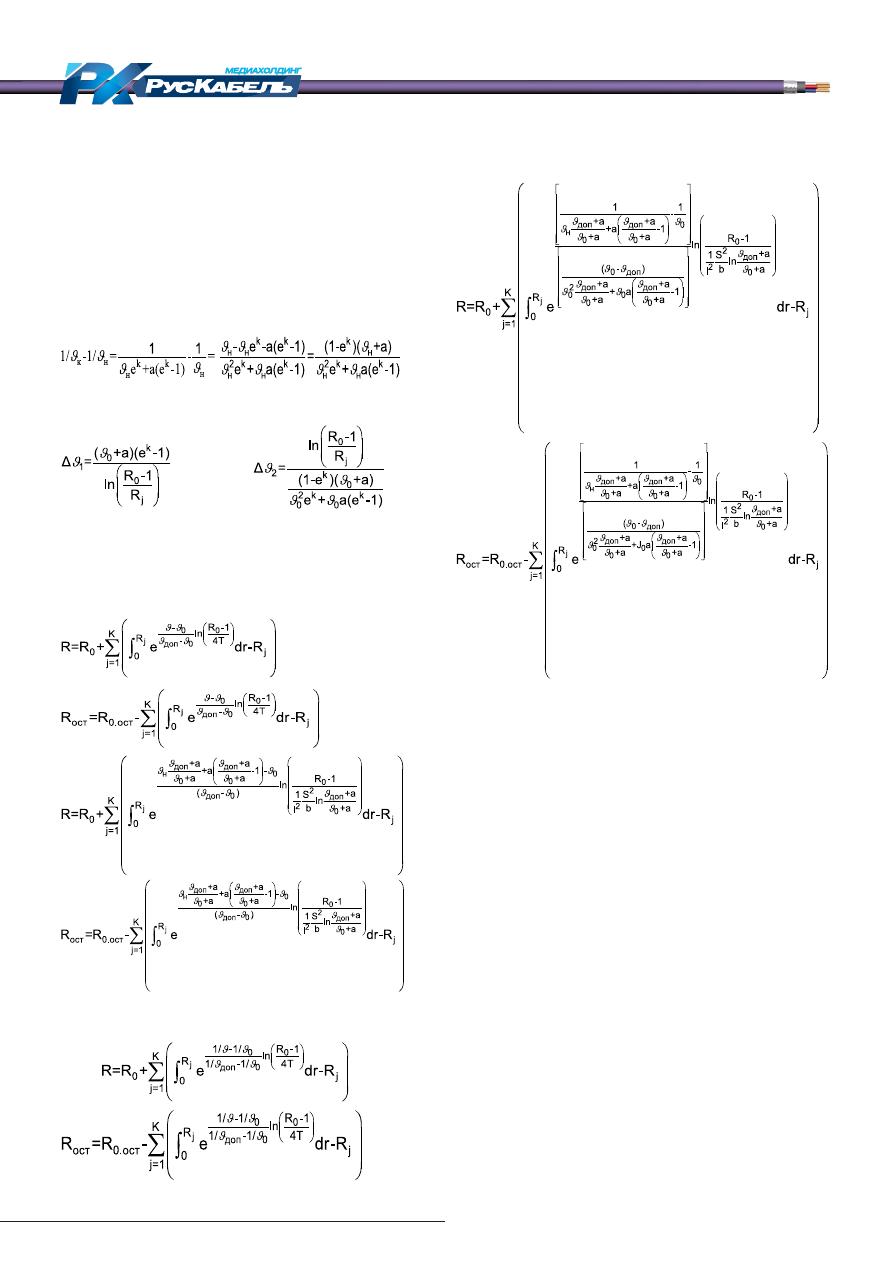
Выполняя математические преобразования, опи-

санные в [1], получим итоговые выражения для опре-
деления фактического сработанного и остаточного
ресурса КЛ для



-градусных правил:

(22),

(23),

(24),

(25).

Для закона Вант Гоффа — Аррениуса эти фор-

мулы для определения фактического сработанного и
остаточного ресурса КЛ запишутся в виде:

(26),

(27),

Page 6

«КАБЕЛЬ-news», № 1, 2014, www.kabel-news.ru



= 70

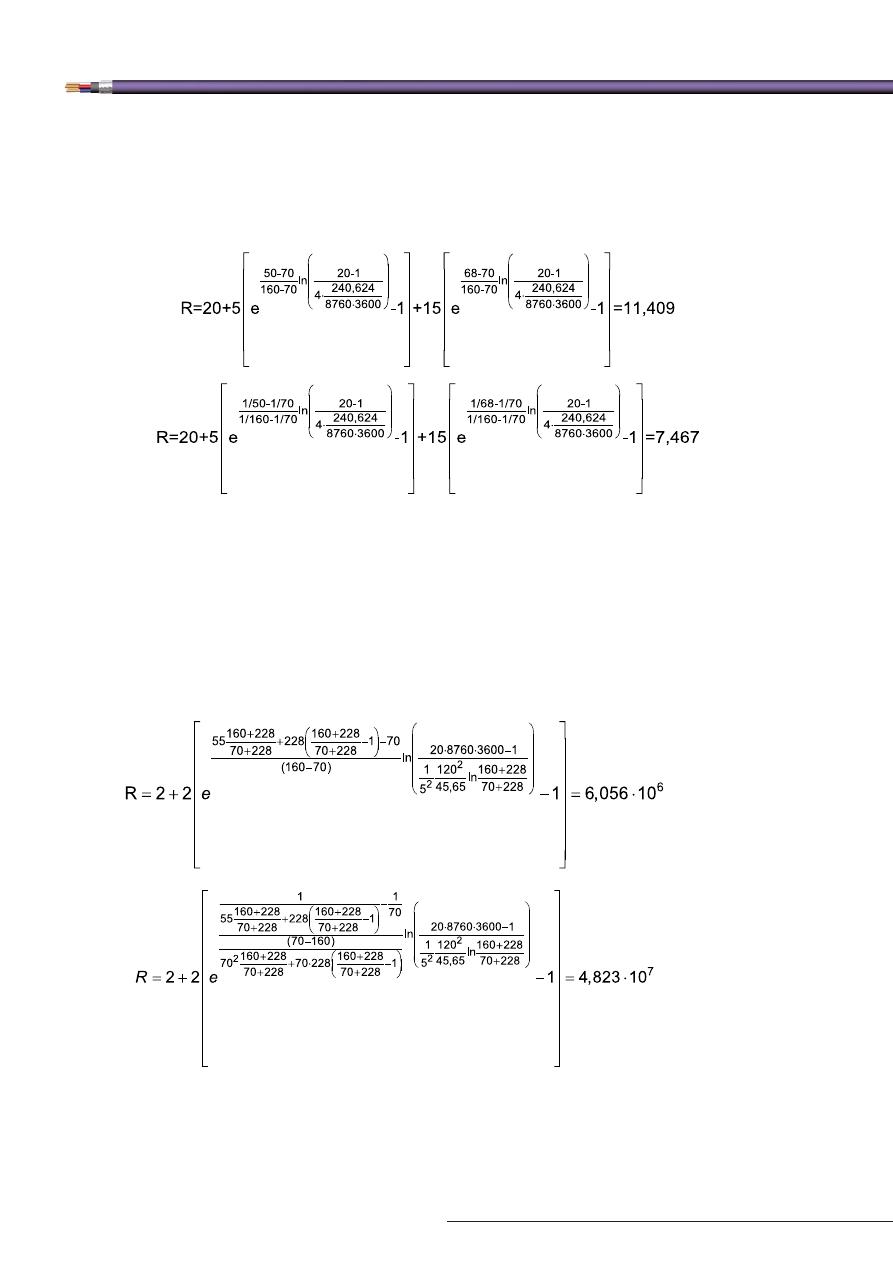
С. Предположим, что данный кабель отработал свой нормативный срок службы, однако 5 лет он экс-

плуатировался с температурой 50

С, а остальные 15 — с температурой 68

С. Рассчитаем по формулам (22)

и (26) фактический сработанный ресурс данного кабеля:

года;

года.

Результаты расчётов по формулам отличаются на 11,4 - 7,5 = 3,9 года. Очевидно, что формула с исполь-

зованием



-градусных правил является более строгой. Поэтому целесообразно пользоваться именно ею,

чтобы избежать аварийных ситуаций с наибольшей вероятностью.

Если далее кабели будут эксплуатироваться при нормативных условиях, то остаточный ресурс опреде-

лится как R

0.ост

= 20 - 11,4 = 8,6 года или R

0.ост

= 20 - 7,5 = 12,5 года. При необходимости с помощью формул

(23) или (27) можно скорректировать эти значения с учётом дальнейших условий эксплуатации.

Пример 2.

Воспользуемся данными и результатами примера 1 и предположим, что данная КЛ в процессе

своей эксплуатации подвергается воздействию тока короткого замыкания величиной 5 кА в течение 2 с.
Начальную температуру при коротком замыкании примем равной 55

С (короткое замыкание произошло в

пределах 5 лет, при которых температура кабеля была равна 55

С). С помощью формул (24) и (28) опреде-

лим фактический сработанный ресурс кабеля за 2 с:

с, или 0,2 года;

с, или 1,5 года.

Результаты расчётов отличаются на 1,5 - 0,2 = 1,3 года. Очевидно, что формула с использованием закона

Вант-Гоффа — Аррениуса является более строгой. Поэтому целесообразнее пользоваться выражением (28)
для большей надёжности результатов расчёта.

Таким образом, если КЛ эксплуатировалась так, как показано в примере 1, и при этом подвергалась

воздействию тока короткого замыкания величиной 5 кА длительностью 2 с. (что равноценно норматив-
ной эксплуатации в первом случае в течение 0,2 года, а во втором — 1,5 года), то фактический срабо-

Актуально

ÐÅÑÓÐÑ ÊÀÁÅËÜÍÛÕ ËÈÍÈÉ

Page 7

«КАБЕЛЬ-news», № 1, 2014, www.kabel-news.ru

Актуально

ÐÅÑÓÐÑ ÊÀÁÅËÜÍÛÕ ËÈÍÈÉ

танный ресурс КЛ составит в первом случае 11,4 +
0,2 = 11,6 года, а во втором: 7,5 + 1,5 = 9 лет. Значе-
ния нормативного остаточного ресурса R

0.ост

будут

соответственно равны: 20 - 11,6 = 8,4 года и 20 - 9 =
11 лет.

При необходимости с помощью формул (23) или

(27) можно скорректировать эти значения с учётом
дальнейших условий эксплуатации. Отметим, что
целесообразно пользоваться наибольшими зна-
чениями фактического сработанного ресурса при
расчётах сразу по обеим формулам, так как это
повышает надёжность полученных результатов.
Поэтому полный (в стационарном режиме и при
коротком замыкании) фактический сработанный
ресурс КЛ имеет смысл рассчитывать следующим
образом: 11,4 + 1,5 = 12,9 года, при этом R

0.ост

20 - 12,9 = 7,1 года. Это есть верхняя граница фак-
тического сработанного ресурса КЛ. Нижнюю гра-
ницу фактического сработанного ресурса КЛ опре-
деляем по выражению: 7,5 + 0,2 = 7,7 года, при этом
R

0.ост

= 20 - 7,7 = 12,3 года.

В заключение отметим, что:

• определение ресурса современных КЛ является

актуальной задачей для обеспечения надёжного
энергоснабжения потребителей;

• для вычисления ресурса КЛ применимы модели

с использованием



-градусных правил и закона

Вант-Гоффа — Аррениуса;

• с целью обеспечения максимальной надёжности

вычислений в качестве результатов расчёта сра-
ботанного ресурса КЛ по формулам



-градусных

правил и закону Вант-Гоффа — Аррениуса необ-
ходимо использовать наибольшие из полученных
значений фактического сработанного ресурса.

ЛИТЕРАТУРА

1. Назарычев А.Н., Андреев Д.А. Методы и матема-

тические модели комплексной оценки техниче-
ского состояния электрооборудования / ГОУ ВПО
«Иван. гос. энерг. ун-т им. В.И. Ленина». — Ива-
ново, 2005. — 224 с.

2. Барнес С. Силовые кабели (конструкция, мон-

таж и эксплуатация): Пер. с англ.; под ред.
С.С. Городецкого. — М.: Энергия, 1971. — 288 с.

3. Канискин В.А., Костенко Э.М., Таджибаев А.И.

Неразрушающий метод определения ресурса
электрических кабелей с полимерной изоляци-
ей в условиях эксплуатации // Электричество. —
1995. — № 5, с. 19—23.

4. Ларина Э.Т. Силовые кабели и высоковольтные

кабельные линии. — 2-е изд. перераб. и доп. —
М.: Энергоатомиздат, 1996. — 464 с.

5. О проверке кабелей на невозгорание при дей-

ствии тока короткого замыкания в сетях соб-
ственных нужд электростанций: Циркуляр № Ц-2-

98 (Э) от 16.03.1998. — М.: РАО «ЕЭС России»,
1998. — 6 с.

6. Таран В.П. Техническая диагностика при эксплуа-

тации электрооборудования. — Киев: Урожай,
1978. — 152 с.

7. Короткевич М.А. Основные направления совер-

шенствования эксплуатации электрических се-
тей. — Минск: Техноперспектива, 2003. — 373 с.

8. Электротехнический справочник. Т. 1. Под ред.

П.Г. Грудинского, 5-е изд., испр. — М.: Энергия,
1975. — 776 с.

9. Белоусов Н.И. Электрические кабели и провода

(теоретические основы кабелей и проводов, их
расчет и конструкции). — М.: Энергия, 1971. —
512 с.

Оригинал статьи: Выбор методики определения сработанного ресурса современных кабельных линий

Читать онлайн

С учётом всё возрастающих требований к бесперебойному электроснабжению потребителей актуальной задачей является выбор расчётных методов достоверного определения сработанного ресурса КЛ с учётом действия эксплуатационных факторов.