Возможности применения устройств синхронизированных векторных измерителей в распределительных сетях

110

РЕЛЕЙНАЯ ЗАЩИТА

И  АВТОМАТИКА

Возможности применения 
устройств синхронизированных 
векторных измерителей 
в распределительных сетях

УДК 621.316.3

Климова

Т

.

Г

.,

к.т.н., доцент кафедры РЗиА

ФГБОУ ВО «НИУ «МЭИ»

Ревякин

В

.

А

.,

магистр кафедры РЗиА

ФГБОУ ВО «НИУ «МЭИ»

Ключевые

слова

:

комплексы УСВИ в распре-

делительных сетях, техно-

логия синхронизированных 

векторных измерений, дис-

кретное преобразование 

Фурье

Условия

работы

распределительных

сетей

, 

их

изменчивость

и

неопределенность

требу

-

ют

более

точного

измерения

режимных

параметров

, 

в

частности

, 

фазового

угла

 (±0,01º), 

и

более

высокого

быстродействия

, 

обеспечивающего

точную

оценку

режимных

пара

-

метров

за

время

, 

меньшее

периода

промышленной

частоты

. 

В

статье

предлагается

мо

-

дернизированное

дискретное

преобразование

Фурье

, 

дающее

быстрый

 (

окно

наблюде

-

ния

 — 10 

мс

), 

точный

и

простой

для

реализации

алгоритм

получения

оценок

параметров

синусоидального

колебания

при

соблюдении

требований

стандарта

МЭК

 C37.118. 

Пред

-

ставлены

результаты

проверки

. 

Разработанный

алгоритм

предлагает

доступное

решение

УСВИ

для

улучшения

возможностей

наблюдения

и

управления

энергосистемой

.

Р

ост  распределенных  энерге-

тических  ресурсов,  таких  как 

возобновляемые  источники

энергии, электромобили и про-

граммы реагирования на спрос, приво-

дит к более краткосрочным и непред-

сказуемым  колебаниям  и  возмуще-

ниям  [1].  Это  требует  более  точного 

и  быстрого  измерения  режимных  па-

раметров распределительной сети для 

управления  возросшей  изменчиво-

стью и неопределенностью при нали-

чии более высокого уровня узкополос-

ных и широкополосных помех и шумов 

измерения [2].

Для  расширения  возможностей 

применения  УСВИ,  в  первую  оче-

редь,  необходимо  совершенствовать 

технологии  УСВИ.  Так,  для  улуч-

шения  характеристик  УСВИ  в  ли-

тературе  предлагаются  различные 

способы  модификации  дискретно-

го  преобразования  Фурье  (Discrete 

Fourier  Transformation,  DFT).  Напри-

мер,  в  [3]  рассмотрено  интеллекту-

альное  дискретное  преобразование 

Фурье (Smart DFT, SDFT), основанное 

на  математической  модернизации 

результата  преобразования  Фурье, 

оно  позволяет  по  формулам  после 

окончания основного преобразования 

Фурье  вычислить  точные  оценки  па-

раметров синусоидального колебания 

при отклонении частоты наблюдаемо-

го сигнала от номинального значения. 

В  данной  работе  предлагается  еще 

одно модернизированное дискретное 

преобразование  Фурье  (окно  наблю-

дения — 10 мс). Это быстрый, точный 

и  простой  для  реализации  алгоритм 

получения оценок параметров синусо-

идального колебания при соблюдении 

требований стандартов Standard IEEE 

C37.118  и  CТО  59012820.29.020.011-

2016. 

Проведено  сопоставление  двух 

алгоритмов (с окнами наблюдения 20 

и 10 мс) при проведении всех опытов 

по СТО 59012820.29.020.011-2016 [4], 

в  котором  регламентированы  опы-

ты,  выполнение  требований  которых 

обес печивают  УСВИ  заданную  точ-

ность  измерений  в  реальных  усло-

виях  работы.  Сопоставление  алго-

ритмов  проводилось  в  программном 

комплексе MatLab. 

ПОСТАНОВКА

ЗАДАЧИ

В  настоящее  время  в  диспетчерских 

центрах  системного  оператора  в  по-

стоянном  режиме  производится  кру-

глосуточное  наблюдение  режимных 

пара мет ров,  обрабатываемых  про-

граммным пакетом SCADA (Supervisory 

Control And Data Acquisition — диспет-

черское  управление  и  сбор  данных). 

SCADA  обеспечивает  замеры  дей-

ствующих  значений  тока  и  напряже-

ния с периодичностью не чаще одного 

раза в секунду. Для наблюдения и ана-

лиза быстродействующих переходных 

процессов этих данных не хватает.

В  связи  с  этим  получили  раз-

витие  системы  мониторинга  пере-

ходных  режимов  WAMS  (Wide  Area 

Measurement System). Данная система 

111

активно внедряется в дополнение 

к  SCADA  и  предполагает  исполь-

зование специальных приборов — 

устройств 

синхронизированных 

векторных измерений (УСВИ) или 

Phasor  Measurement  Unit  (PMU). 

УСВИ  определяют  векторы  (то 

есть действующие значения и фа-

зовые углы) напряжения и тока для 

каждой фазы и для прямой после-

довательности, по ним вычисляют-

ся  мощности  и  другие  режимные 

параметры  энергосистемы.  Так-

же  УСВИ  выполняют  измерения 

частот  и  скорости  их  изменения, 

как для частоты каждой фазы, так 

и для прямой последовательности. 

Все измерения синхронизированы 

по  времени  с  применением  гло-

бальной  системы  позиционирова-

ния (GPS) или GLONASS с точно-

стью синхронизации не хуже 1 мкс. 

Таким  образом,  системы  WAMS 

обеспечивают глобальное статиче-

ское и динамическое наблюдение 

векторов  режимных  параметров 

энергосистем,  синхронизирован-

ных  по  времени,  с  возможностью 

автоматизации  обработки  резуль-

татов наблюдения.

Начало  работ  по  применению 

технологии  синхронизированных 

векторных  измерений  в  России 

стоит  датировать  2005  годом  [5]. 

Производство первых отечествен-

ных УСВИ начинается в 2006 году. 

В  настоящее  время  установлено 

более  800  УСВИ  по  России.  Со-

гласно  СТО  59012820.29.020.001-

2016  основными  критериями  вы-

бора  мест  установки  являются 

напряжение  и  мощность  станций 

и  подстанций,  как  правило,  это 

турбогенераторы АЭС и ТЭС мощ-

ностью 200 МВт и более, гидроге-

нераторы ГЭС и ГАЭС мощностью 

100  МВт  и  более,  автотрансфор-

маторы, входящие в контролируе-

мое сечение (со стороны высшего 

класса напряжения), ЛЭП высшего 

класса напряжения 220 кВ и выше.

Качество  и  динамика  полу-

чаемой  УСВИ  информации  вы-

зывает  интерес  к  применению  их 

и при других уровнях напряжения, 

в распределительных сетях, а так-

же  при  распределенной  генера-

ции  электроэнергии,  то  есть  при 

производстве  энергии  на  уровне 

распределительной  сети  или  на 

стороне  потребителя,  включен-

ного  в  сеть.  Но  для  реализации 

преимуществ  и  удобств,  которые 

несет с собой распределенная ге-

нерация  электроэнергии,  необхо-

димо  обеспечивать  устойчивость 

работы,  регулирование  и  под-

держание  нормальных  режимов, 

предотвращать  аварийные  ситуа-

ции и др. Все вышеперечисленное 

может  создать  новые  проблемы 

при  планировании,  мониторинге, 

контроле,  управлении  и  защите 

распределительной  сети,  что  по-

требует постоянного анализа элек-

трических  параметров  в  условиях 

повышенной динамической измен-

чивости системы [2]. Здесь же по-

казано,  что  эти  информационные 

проблемы могут быть решены при 

использовании  УСВИ.  В  зарубеж-

ной  литературе  уже  встречается 

термин  для  устройств  СВИ,  уста-

новленных  в  распределительных 

сетях, — микроУСВИ (μPMU). 

Основное  нововведение  по 

сравнению  с  традиционными 

УСВИ  —  более  высокая  точность 

измерений  фазового  угла  вплоть 

до  небольших  долей  градуса 

±0,01º.  Подобное  различие,  во-

первых,  объясняется  наличием 

более  высоких  уровней  гармоник 

по  сравнению  с  сетями  высшего 

напряжения  [2],  во-вторых,  мень-

шими  перетоками  мощностей,  со-

ответственно  и  более  короткими 

линиями,  по  которым  эти  мощ-

ности  протекают.  Обычное  УСВИ 

с  ошибкой  оценки  ±0,1º  не  может 

обеспечить  достаточной  точности 

для оценки режима при распреде-

ленной генерации электроэнергии. 

Кроме того, к микроУСВИ предъяв-

ляются  требования  повышенной, 

по  сравнению  с  УСВИ  для  высо-

кого  напряжения,  помехоустойчи-

востью.  Для  широкого  использо-

вания в распределительный сетях 

микроУСВИ  должны  быть  суще-

ственно  дешевле  традиционных 

УСВИ.  Здесь  же  высказывается 

мнение  о  необходимости  приме-

нения бо̀льшей частоты дискрети-

зации  (fs)  для  получения  256  или 

512 дискретных отсчетов на пери-

од промышленной частоты взамен 

80 или 96 для традиционных УСВИ 

соответственно. 

Все  вышеперечисленные  фак-

торы предполагают использование 

возможностей  микроУСВИ  с  це-

лью  поддержания  устойчивой  ра-

боты распределительной сети.

ХАРАКТЕРИСТИКА

ПРЕДЛАГАЕМОГО

АЛГОРИТМА

Далее  рассматриваются  несколь-

ко вариантов реализации алгорит-

мов  дискретного  преобразования 

Фурье:  классический  алгоритм 

DFT [6], с оконной функцией дли-

тельностью  в  один  период  про-

мышленной  частоты  (full-cycle 

DFT,  далее  —  FCDFT)  и  DFT  по-

ловины  цикла  промышленной  ча-

стоты,  то  есть  с  оконной  функци-

ей  длительностью  в  полпериода 

промышленной частоты (half-cycle 

DFT, далее — HCDFT) [7]. Рассма-

триваемые  алгоритмы  DFT  явля-

ются базовыми для использования 

в фильтрах Фурье.

Модифицированный  алгоритм 

DFT  разрабатывался  с  возможно-

стью применения его в сетях с рас-

пределенной  генерацией,  то  есть 

алгоритм  должен  обеспечивать 

максимальное 

быстродействие 

и точность [2].

Для  ускорения  алгоритма  це-

лесообразно  использовать  DFT 

половинного  цикла.  В  литературе 

встречаются  использования  тра-

диционного  DFT  с  оконной  функ-

цией длительностью в полпериода 

промышленной  частоты.  По  срав-

нению c FCDFT в HCDFT увеличи-

вается  погрешность  определения 

параметров  входных  сигналов 

и наблюдаются худшие фильтрую-

щие свойства. 

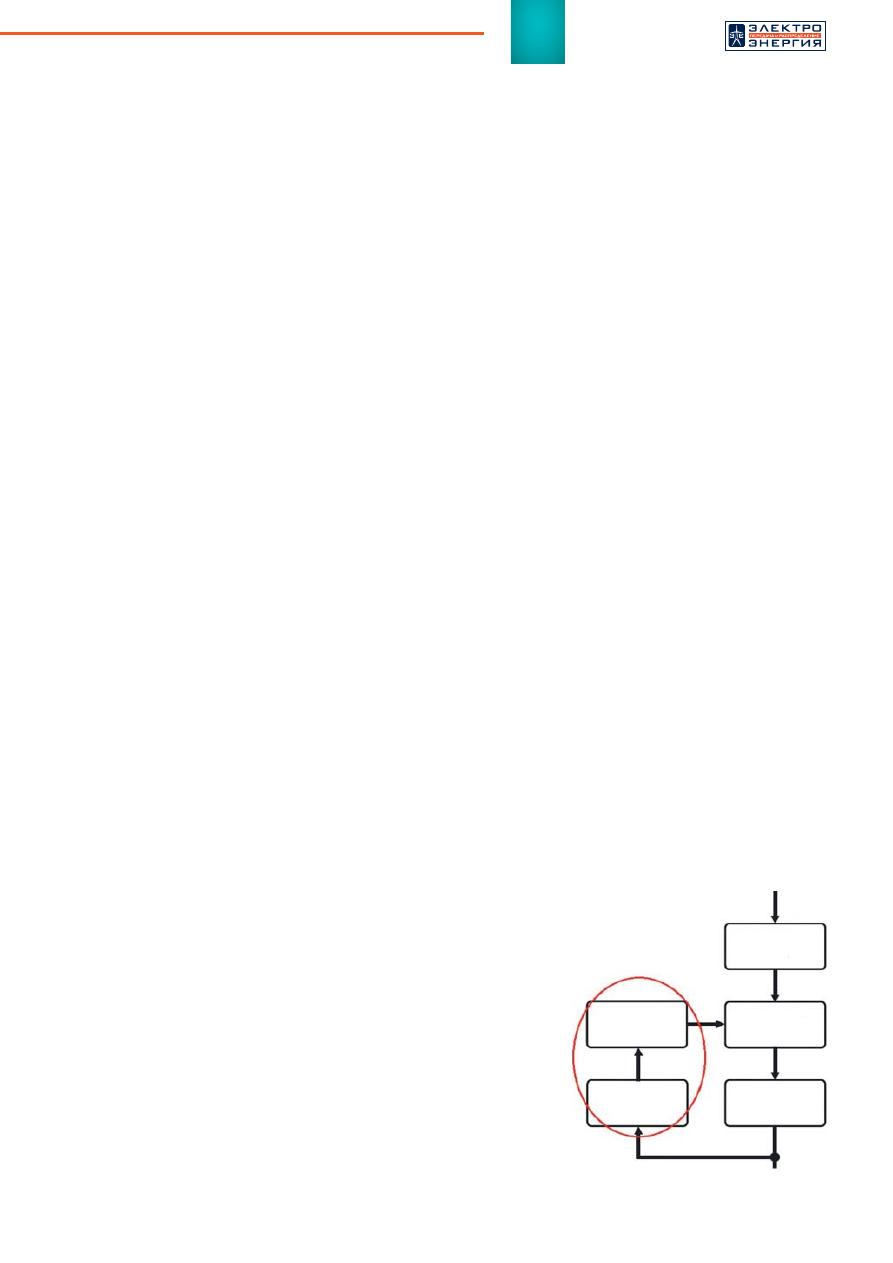
Основная  особенность  из-

вестных алгоритмов DFT с любой 

оконной  функцией  показана  на 

рисунке 1 —  после оценки часто-

ты  тестового  сигнала  происходит 

подстройка  частоты  дискретиза-

Рис

. 1. 

Дискретизация

входных

сиг

-

налов

в

методах

 DFT [7]

Подстройка

частоты

дискретизации

Оценка

частоты

АЦП

Устройство

выборки

и хранения

Фильтр

низкой

частоты

x

(

t

)

x

[

n

]

f

№

 6 (63) 2020

112

ции,  что  вносит  дополнительную 

задержку  при  оценке  режимных 

параметров сети.  

Предлагаемый  модифициро-

ванный  полупериодный  алгоритм 

DFT  (modernized  half-cycle  DFT, 

далее — MH_DFT) не требует под-

стройки  частоты  дискретизации 

и обеспечивает подавление апери-

одической составляющей. 

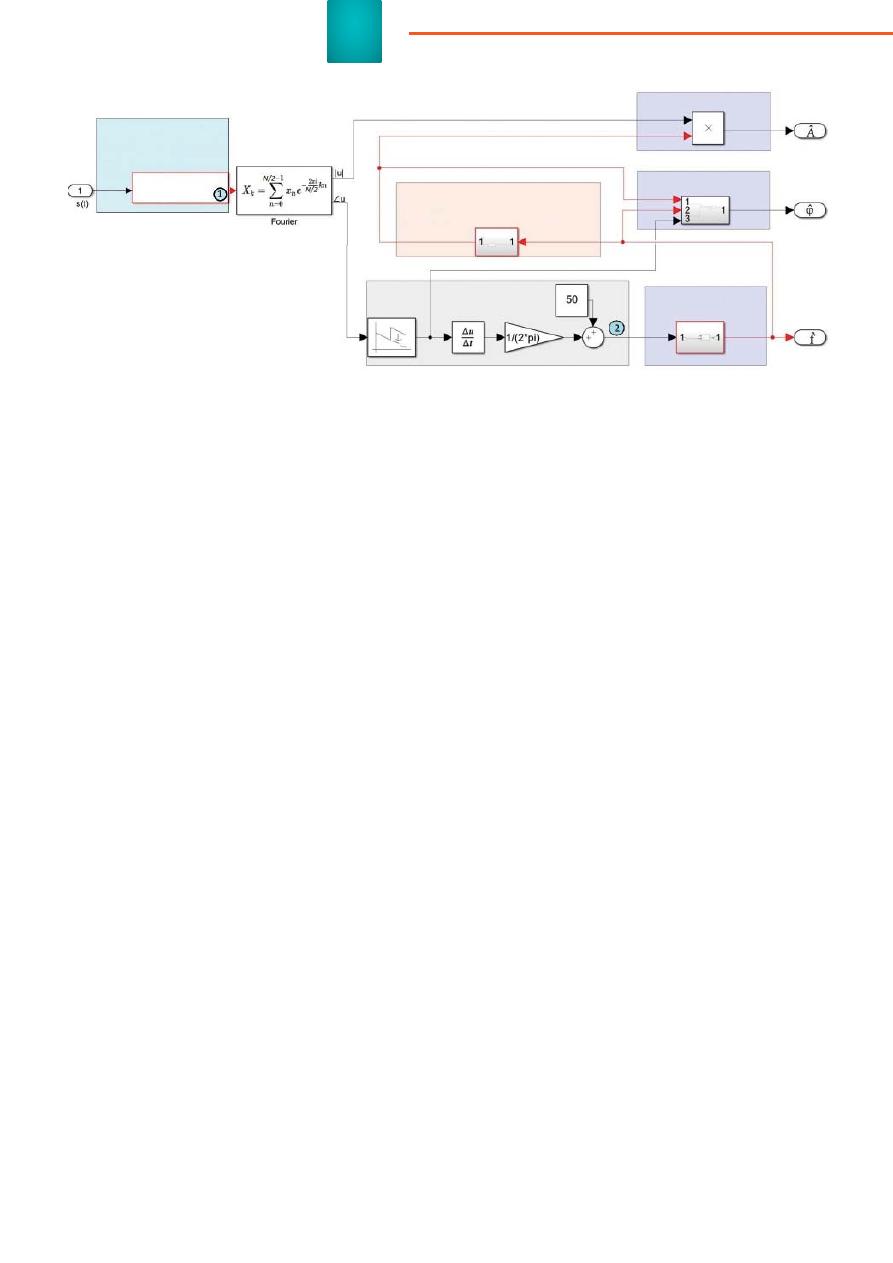
На  структурной  схеме  рисун-

ка 2 показаны все действия, необ-

ходимые  при  оценке  параметров 

входного  сигнала  при  значениях 

частоты  входного  сигнала,  отлич-

ной от номинальной частоты DFT. 

Как  известно,  фильтр  Фурье, 

использующий  любой  вариант 

DFT,  при  оценке  параметров  си-

нусоидальных  сигналов  с  часто-

той,  равной  частоте  обработки 

фильтра,  имеет  наименьшие  по-

грешности.  Наибольшие  погреш-

ности  в  измерениях  необходимых 

характеристик 

синусоидальных 

колебаний возникают при отклоне-

нии  частоты  входного  сигнала  от 

номинального  значения  частоты 

фильтра.  Поэтому  целесообразно 

описать  предлагаемый  алгоритм 

DFT  именно  в  сертификационном 

опыте ступенчатого изменения ча-

стоты  входного  синусоидального 

сигнала. Этот опыт входит в серию 

сертификационных 

испытаний 

УСВИ [4].

Далее  представлены  экспе-

риментальные  результаты,  полу-

ченные  при  условии  выполнения 

требований  стандарта  к  проверке 

точности  измерений  УСВИ  в  сер-

тификационных испытаниях.

В  задачах  при  наличии  апе-

риодической  составляющей  тре-

буется  ее  подавление.  Для  этого 

либо  оцениваются  ее  параметры 

любым способом и в дальнейшем 

используются,  либо  апериодиче-

ская составляющая удаляется при 

дифференцировании 

входного 

сигнала, блок 1 (рисунок 2).

В точке 2 блока «Предваритель-

ная оценка частоты» при отклоне-

нии  частоты  входного  сигнала  от 

номинальной  частоты,  использу-

емой в фильтре Фурье, в измере-

ниях  частоты  наблюдаются  коле-

бательные  изменения.  Обычно 

далее  происходит  подстройка  ча-

стоты  дискретизации  (номиналь-

ной) (рисунок 1). Предлагается при 

использовании полученной оценки 

частоты  определить  число  слага-

емых  в  формуле  фильтра  Фурье 

(рисунок 2), то есть вычислить чис-

ло  выборок  сигнала,  соответству-

ющих  половине  периода  частоты 

входного  сигнала  при  сохранении 

фиксированной  частоты  дискре-

тизации. Это реализуется в блоке 

«Коррекция частоты, расчет пери-

ода». 

Коррекция  частоты  может  про-

исходить  тремя  способами:  тео-

ретическим, эмпирическим и с ис-

пользованием  методов  оптималь-

ной аппроксимации функций.

Теоретический  метод  предпо-

лагает  использование  формул 

оконного  преобразования  Фурье 

для  получения  точных  значений 

корректирующих  коэффициентов. 

При  этом  устанавливается  фик-

сированная  длина  окна,  равная 

0,02  с,  и  вычисляется  значение 

фазы, частоты и амплитуды вход-

ного  синусоидального  сигнала 

с  частотой,  отличающейся  от  но-

минального  значения.  Формулы 

оценок  дают  формулы  корректи-

рующих коэффициентов для иско-

мых параметров входного сигнала. 

Метод  громоздкий.  Кроме  этого, 

можно показать, что при обработке 

точными  формулами  (например, 

[3])  зашумленного  сигнала  суще-

ственно  увеличивается  погреш-

ность измерений.

Эмпирический

  метод  основан 

на рассмотрении свойств экспери-

ментально полученных первичных 

оценок искомых параметров вход-

ного сигнала. Согласно [4], одним 

из  сценариев  основных  тестов 

УСВИ класса M в статических усло-

виях  является  проверка  работы 

алгоритма при различных значени-

ях частоты, в диапазоне 45÷55 Гц. 

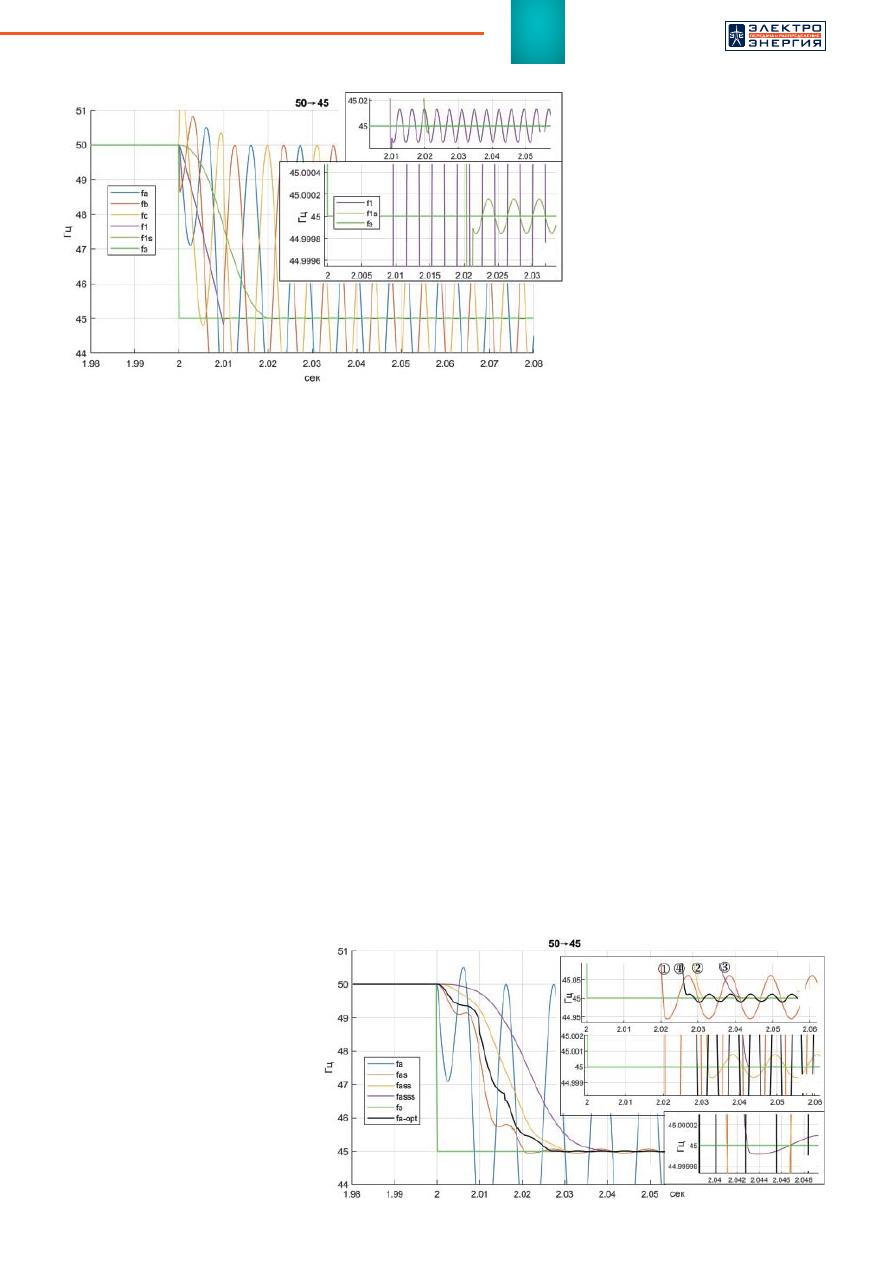
Далее на рисунке 3а показаны пер-

вичные  оценки  частоты  фазных 

напряжений  в  момент  изменения 

частот  входного  сигнала  с  50  до 

45  Гц  при  использовании  полупе-

риодного  алгоритма  DFT  (H_DFT) 

с  оконной  функцией  длительно-

стью  в  полпериода  промышлен-

ной  частоты  без  дополнительной 

коррекции.  Это  синусоидальные 

колебания  вокруг  частоты  45  Гц 

(постоянный  сдвиг)  с  амплитудой 

5 Гц, частотой 2×45 Гц и соответ-

ствующими фазами (fa, fb, fc — ри-

сунок  3а).  Суммирование  оценок 

частот  трех  фаз  позволяют  полу-

чить с высокой точностью первич-

ную  оценку  частоты  напряжения 

прямой  последовательности  f1, 

имеющую колебательную погреш-

ность  (рисунок  3б)  менее  0,02  Гц 

через  0,01  с  (полпериода)  после 

начала возмущения. 

Полученная  оценка  частоты 

позволяет  определить  число  дис-

кретных  отсчетов  фиксированной 

частоты  дискретизации,  соответ-

ствующих  периоду  измеренного 

значения  частоты  входного  коле-

бания. 

Формирование

корректирующих

коэффициентов

Подавление

апериодической

составляющей

Вариативные

формулы

Предварительная

оценка частоты

Коррекция амплитуды

Коррекция фазы

Коррекция частоты,

расчет периода

Рис

. 2. 

Структурная

схема

пред

-

лагаемого

модифицированного

алгоритма

 DFT (MH_DFT) 

с

оконной

функцией

длительностью

в

полпе

-

риода

промышленной

частоты

РЕЛЕЙНАЯ ЗАЩИТА

И  АВТОМАТИКА

113

Усреднение  (сглаживание)  ко-

лебательной  погрешности  на  пе-

риоде  ее  колебаний  позволяет 

получить высокую точность оценок 

f1s (рисунок 3в). Итоговая погреш-

ность является также колебатель-

ной  погрешностью  с  амплитудой 

менее 0,0002 Гц, полученной при-

мерно через 0,02 с (один период) 

после начала возмущения. Эта по-

грешность  существенно  меньше 

и результат получен быстрее, чем 

требуется  по  Стандарту  [4]  для 

любого класса УСВИ (допустимая 

погрешность 0,001 Гц при окне об-

работки 0,08 с).

Значительно сложнее ситуация 

наблюдается  при  оценке  частот 

фазных напряжений, которые рас-

сматриваются по отдельности, без 

учета других фаз. Поэтому в этом 

случае рассмотрены возможности 

и  метода  оптимальной  аппрокси-

мации функций. 

Метод 

оптимальной

аппрокси

-

мации

 использует предполагаемую 

функциональную зависимость для 

оценки  параметров,  определяю-

щих эту зависимость, при обработ-

ке  массива  данных.  При  данном 

изменении частоты это колебание 

с постоянным сдвигом (45 Гц), ам-

плитудой (5 Гц), частотой (2×45 Гц) 

и начальной фазой (зависит от мо-

мента  начального  возмущения). 

В  реальной  ситуации  указанные 

параметры функциональной зави-

симости  неизвестны.  Этот  метод 

требует  максимальных  вычисли-

тельных мощностей.

На рисунке 4 показано исполь-

зование  двух  методов  (эмпириче-

ского  и  оптимальной  аппроксима-

ции)  для  оценки  частоты  фазных 

напряжений при изменении часто-

ты входного сигнала от 50 до 45 Гц. 

Кривые  (1÷3)  показывают  посте-

пенное  уменьшение  колебатель-

ной погрешности: 0,05 Гц за пери-

од (fas, однократное сглаживание), 

менее 10

-3

 Гц за полтора периода 

(fass,  двукратное  сглаживание), 

в  итоге,  до  погрешности  10

-5

  Гц 

за  два  периода  промышленной 

частоты  (fasss,  трехкратное  сгла-

живание).  Кривая  (4)  (fa-opt)  по-

казывает оценку частоты методом 

оптимальной аппроксимации.

Подобный  колебательный  ха-

рактер  имеют  также  первичные 

оценки  амплитуды  и  фазы  вход-

ных сигналов.

Корректирующие  коэффициен-

ты формируются в зависимости от 

скорректированной  оценки  часто-

ты.  Умножение  текущей  сглажен-

ной оценки (момент ii) амплитуды 

(красная кривая) на коэффициент 

kfa(ii) = fo/fas(ii) существенно повы-

шает точность полученной оценки 

амплитуды. Чем точнее определе-

на  частота,  тем  точнее  получено 

значение  амплитуды.  Подобную 

закономерность  можно  просле-

дить и при оценке фазы.  

При  совпадении  частоты  вход-

ного сигнала и номинального зна-

чения  промышленной  частоты 

(частоты  фильтра  Фурье)  эти  ко-

эффициенты равны единице.

Поскольку  в  стандарте  [4] 

требуется  обеспечить  заданную 

точность  режимных  параметров 

прямой  последовательности,  на 

рисунке  5  и  далее  представляют-

ся  результаты  оценок  параметров 

прямой последовательности.

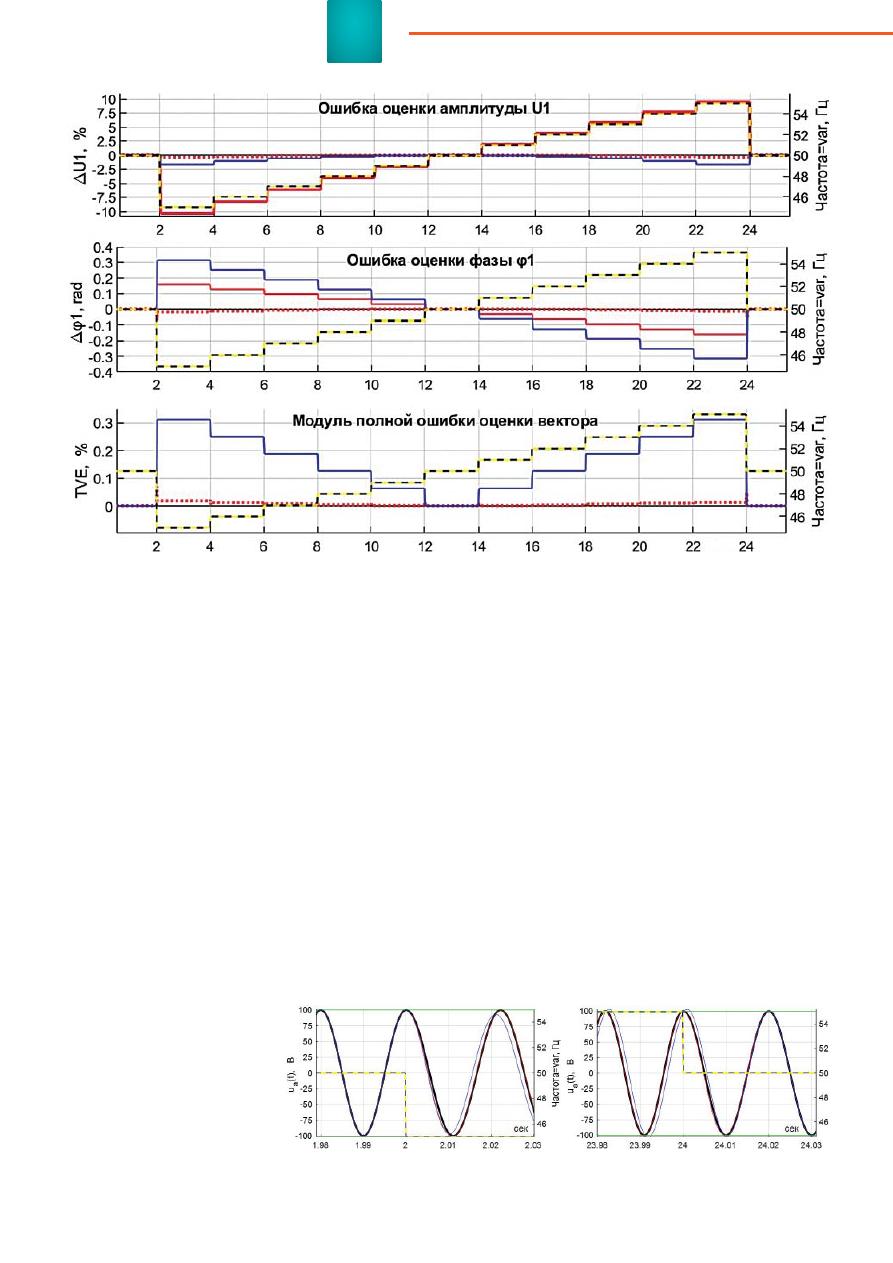
Стандарт [4] требует сопостави-

тельной иллюстрации оценки пара-

метров входного тестового сигнала 

во всем диапазоне изменения этих 

параметров.  Пример  такой  иллю-

страции представлен на рисунке 5. 

Здесь  показаны  рассчитанные 

ошибки  измерений  амплитуды 

и фазы синхронизированного век-

тора напряжения (рисунки 5а и 5б) 

при подаче тестового сигнала. Эти 

отдельные  ошибки  позволяют  вы-

числить полную ошибку синхрони-

зированного  вектора  (total  vector 

error,  TVE)  —  величину,  характе-

ризующую отклонение амплитуды 

и фазы измеренного вектора от их 

заданных  значений  в  совокупно-

сти. Допускаются погрешности из-

мерения фазы Δφ<0,1º, TVE<1%. 

Пунктирная линия на всех гра-

фиках  рисунка  5  показывает  за-

данное  изменение  режимного 

параметра,  в  данном  случае  — 

частоты  тестового  сигнала,  изме-

нение  показано  на  правых  осях. 

Синие  характеристики  на  обо-

их  рисунках  относятся  к  оценке 

амплитуды  традиционным  алго-

ритмом  DFT  с  оконной  функци-

Рис

. 3. 

Возможности

 MH_DFT 

при

оценке

частоты

 f

э

 (

эталонной

) 

напряже

-

ния

прямой

последовательности

 (

здесь

и

далее

индекс

 «s» 

в

переменных

означает

сглаживание

колебаний

)

Рис

. 4. 

Возможности

 MH_DFT 

при

оценке

частоты

напряжения

любой

фазы

б)

в)

а)

а)

б)

в)

г)

№

 6 (63) 2020

114

ей  длительностью  в  один  период 

промышленной  частоты.  Красные 

характеристики  относятся  к  оцен-

ке амплитуды алгоритмом НСDFT 

с  оконной  функцией  длительно-

стью в полпериода промышленной 

частоты, при этом точечные крас-

ные характеристики получены при 

коррекции  оценок  с  учетом  пред-

варительной оценки частоты вход-

ного  сигнала.  Сравнение  красных 

кривых  показывает  существенное 

уменьшение  погрешностей  изме-

рений  параметров  тестового  сиг-

нала  при  использовании  алгорит-

ма MH_DFT.

Точность  получаемых  оценок 

числовых  параметров  тестовых 

сигналов можно оценить при срав-

нении  этих  сигналов  с  восстанов-

ленными  по  соответствующим 

оценкам  сигналов  (рису-

нок 6). Рассматривается пе-

реход частоты от 50 к 45 Гц 

(рисунок 6а) и от 55 к 50 Гц 

(рисунок 6б).

В  обеих  ситуациях  сиг-

нал,  восстановленный  по 

оценкам  MH_DFT  (красные 

кривые),  вследствие  незна-

чительных 

погрешностей 

практически  всегда  визу-

ально совпадает с тестовым 

сигналом  (черные  кривые) 

через  0,01  с.  Видно,  что  сигнал, 

восстановленный  по  оценкам 

FСDFT (синие кривые), всегда име-

ет  фазовый  сдвиг  и  погрешность 

по амплитуде при неноминальной 

частоте  тестового  сигнала.  Это 

согласовывается  с  результатами, 

представленными на рисунке 5.

Существенно меньше проблем 

возникает  в  различных  алгорит-

мах  DFT  в  ситуациях  изменения 

амплитуд  и  фаз  тестовых  сигна-

лов  с  фиксированной  номиналь-

ной  частотой.  Поскольку  частота 

тестовых  сигналов  равна  номи-

нальной,  не  требуется  перерас-

чет  длительностей  периода  при 

оценке  параметров  и  коэффици-

енты  коррекции  оценок  амплитуд 

и фаз автоматически определяют-

ся  алгоритмом  единичными.  Для 

иллюстрации  результатов  работы 

алгоритмов  достаточно  показать 

ошибки  оценок  изменяющихся 

параметров  тестовых  сигналов 

и  проиллюстрировать  восстанов-

ление тестовых сигналов. 

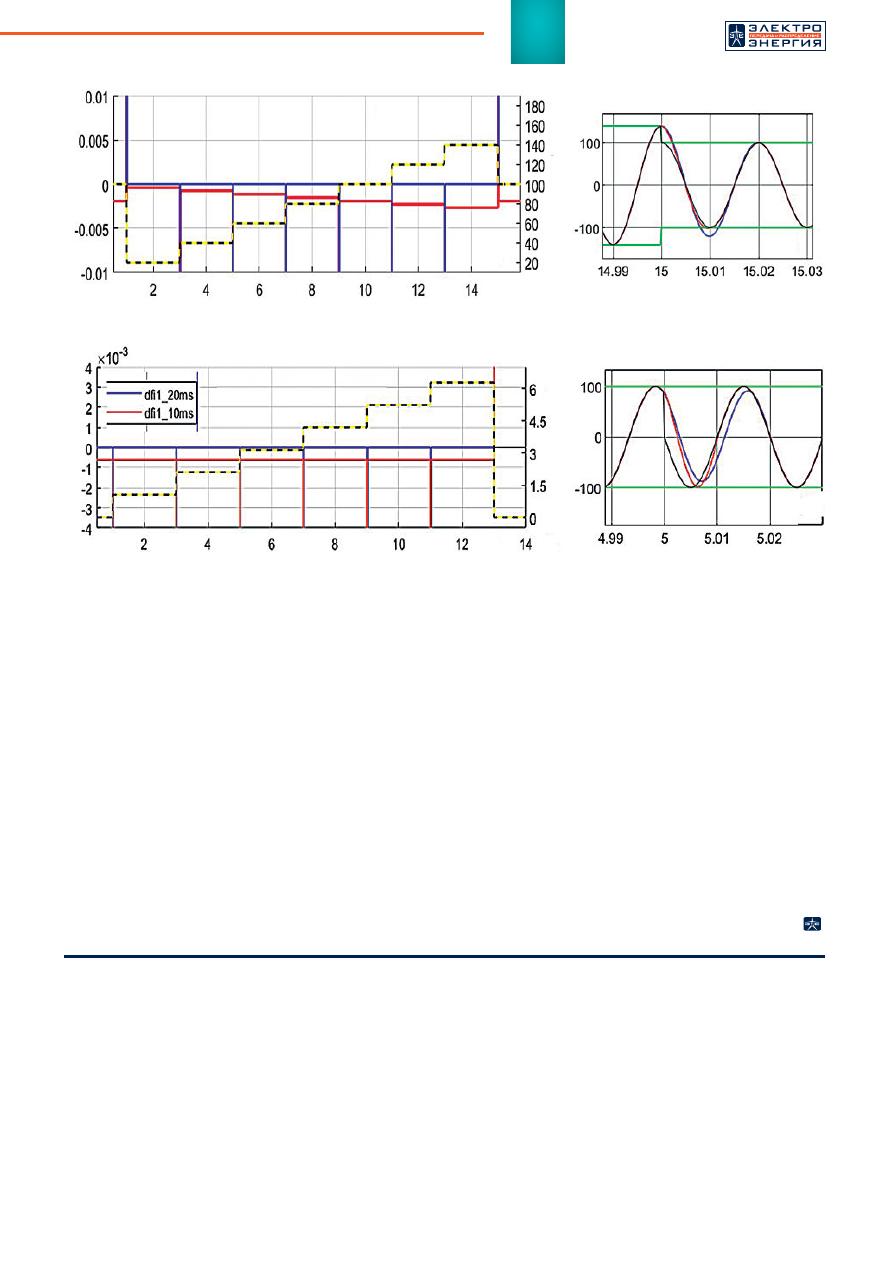
На  рисунке  7  изменение  пара-

метра тестового сигнала, в данном 

опыте — амплитуды тестового сиг-

нала, показано пунктирной линией 

(рисунок  7а),  значения  показаны 

на  правых  осях,  а  также  зелены-

ми линиями (рисунок 7б). Ошибка 

оценки  амплитуды  чрезвычайно 

мала  для  обоих  алгоритмов  DFT 

(с окном наблюдения 20 и 10 мс).

На  рисунке  8  изменение  фазы 

тестового  сигнала  показано  пун-

ктирной  линией,  диапазон  изме-

нения 0÷2



 (рисунок 8а), значения 

показаны на правой оси. И в этом 

Рис

. 6. 

Иллюстрация

точности

определения

оценок

алгоритмом

 F

С

DFT (

синие

кривые

) 

и

алгоритмом

 MH_DFT (

красные

кривые

) 

при

восстановлении

входных

синусоидальных

колебаний

по

оценкам

числовых

характеристик

синусоид

при

двух

значениях

изменения

частоты

, 

значения

которых

указаны

на

правых

осях

РЕЛЕЙНАЯ ЗАЩИТА

И  АВТОМАТИКА

Рис

. 5. 

Сопоставление

точности

алгоритмов

 FCDFT (

синие

характеристики

), HCDFT (

красные

сплошные

линии

) 

и

 MH_DFT (

красные

точечные

линии

) 

при

ступенчатом

изменении

частоты

тестового

сигнала

в

диапазоне

 45÷55 

Гц

в)

сек.

сек.

сек.

а)

б)

а)

б)

115

случае ошибка оценки фазы чрез-

вычайно  мала  для  обоих  алго-

ритмов DFT (с окном наблюдения 

20 и 10 мс).

Сравнение  восстановленных 

по  оценкам  параметров  синусои-

дальных  колебаний  с  входными 

тестовыми сигналами (рисунки 7б 

и  8б)  показывает  точность  и  ско-

рость  определения  оценок  алго-

ритмом  FСDFT  (синие  кривые) 

и  алгоритмом  MH_DFT  (красные 

кривые).  Красные  кривые  после 

первых  10  мс  всегда  совпадают 

с тестовым сигналом (черные кри-

вые),  синие  кривые  приближают-

ся  к  истинным  значениям  только 

к концу периода.

ВЫВОДЫ

В  работе  предлагается  модерни-

зированное  дискретное  преобра-

зование  Фурье,  дающее  быстрый 

(окно  наблюдения  —  10  мс),  точ-

ный  и  простой  для  реализации 

алгоритм  получения  оценок  па-

раметров  синусоидального  коле-

бания.  Алгоритм  проверен  при 

проведении  всех  сертификацион-

ных  опытов,  регламентированных 

в  стандарте  [4],  с  соблюдением 

соответствующих 

требований. 

Статические  и  динамические  из-

менения параметров тестовых сиг-

налов определяются с заявленной 

точностью  и  быстродействием, 

превышающими  аналогичные  па-

раметры  алгоритма  с  окном  на-

блюдения 20 мс. 

Быстрые  и  точные  оценки  ис-

комых  электрических  параметров 

позволяют  решать  с  требуемы-

ми  точностью  и  быстродействи-

ем  задачи,  которые  необходимы 

в  распределительных  сетях  и  се-

тях  с  распределенной  генераци-

ей  (например,  анализ  топологии 

сети,  мониторинг  поведения  на-

грузок  в  реальном  времени,  об-

наружение,  классификация  со-

бытий и места их возникновения), 

поэтому  предлагаемый  алгоритм 

может быть применен для расши-

рения  возможностей  наблюдения 

и управления энергосистемой.  

Рис

. 7. 

Опыт

ступенчатого

изменения

амплитуды

тестового

сигнала

: 

а

) 

ошибка

оценки

амплитуды

; 

б

) 

восстанов

-

ленные

по

оценкам

числовых

характеристик

тестовые

сигналы

а)

б)

Ошибка оценки амплитуды U1



U1, %

Амплит

уда U1 = var

, В

Рис

. 8. 

Опыт

ступенчатого

изменения

фазы

тестового

сигнала

: 

а

) 

ошибка

оценки

фазы

; 

б

) 

восстановленные

по

оценкам

числовых

характеристик

тестовые

сигналы

а)

б)

Ошибка оценки фазы 



1



1, rad

фа

за 



1 = var

, rad

ЛИТЕРАТУРА / REFERENCES

1.  Sexauer J., Javanbakht P., Mohagheghi S. Phasor Measurement 

Units for the Distribution Grid: Necessity and Benefi ts / IEEE PES 

Innovative  Smart  Grid  Technologies  Conference  (ISGT),  2013, 

pp. 1-6. 

2.  Stewart  E.,  von  Meier  A.,  McEachern  A.,  Andersen  M.,  Meh-

rmanesh L. Precision Micro-Synchrophasors for Distribution Sys-

tems: A Summary of Applications / IEEE Transactions on Smart 

Grid, november 2017, vol. 8, no. 6, pp. 2926-2936.

3.  Gurusinghe  D.R.,  Ouellette  D.,  Rajapakse  A.D.  Implementation 

of Smart DFT-based PMU Model in the Real-Time Digital Simula-

tor / The International Conference on Power Systems Transients 

(IPST). Conference at Seoul, Republic of Korea, June 2017.

4.  СТО  59012820.29.020.011-2016.  Стандарт  релейная  защита 

и  автоматика.  Устройства  синхронизированных  векторных 

измерений. Нормы и требования. URL: https://so-ups.ru/fi lead-

min/fi les/laws/standards/sto_synhro_vector.pdf.

Company Standard STO 59012820.29.020.011-2016. Relay pro-

tection  and  automation  standard.  Phasor  measurement  units. 

Norms and requirements.

5.  Система мониторинга переходных режимов Единой энергети-

ческой системы России. URL: https://www.smpr.technology.

Wide-area measurement system of the Unifi ed Power System of 

Russia.

6.  Kaiser J.F. On a simple algorithm to calculate the ‘energy’ of a sig-

nal  in  Proc  /  IEEE  Int.  Conf. Acoust.,  Speech,  Signal  Process. 

Albuquer-que, 1990, vol. 1, pp. 381-384.

7.  Phadke A.G., Thorp J.S. Synchronized Phasor Measurements and 

Their Applications, Springer, 2008, pp. 9.

а)

б)

№

 6 (63) 2020