Оригинал статьи: Возможности применения устройств синхронизированных векторных измерителей в распределительных сетях
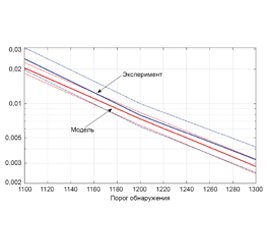
Условия работа распределительных сетей, их изменчивость и неопределенность требуют более точного измерения режимных параметров, в частности, фазового угла (±0,01º), и более высокого быстродействия, обеспечивающего точную оценку режимных параметров за время, меньшее периода промышленной частоты. В статье предлагается модернизированное дискретное преобразование Фурье, дающее быстрый (окно наблюдения — 10 мс), точный и простой для реализации алгоритм получения оценок параметров синусоидального колебания при соблюдении требований стандарта МЭК C37.118. Представлены результаты проверки. Разработанный алгоритм предлагает доступное решение УСВИ для улучшения возможностей наблюдения и управления энергосистемой.