84
КАЧЕСТВО
ЭЛЕКТРОЭНЕРГИИ
Векторное управление
режимами электропередачи
на основе асинхронизированных
синхронных машин
УДК 621.316.7:621.3.05
В
статье
рассмотрена
система
векторного
управления
установившимися
режимами
,
переходными
процессами
и
потокораспределением
активной
мощности
в
сложнозам
–
кнутой
неоднородной
электрической
сети
.
Система
управления
предназначена
для
контроля
асинхронизированного
электромеханического
преобразователя
частоты
(
АСЭМПЧ
),
врезанного
в
линию
электропередачи
.
Получившаяся
система
предназначена
для
качественного
улучшения
условий
протекания
переходных
процессов
,
вызванных
короткими
замыканиями
,
и
улучшения
параметров
установившихся
режимов
сети
.
При
этом
предложенный
подход
позволяет
существенно
повысить
качество
и
надежность
пи
–
тания
потребителей
после
ликвидации
коротких
замыканий
.
Рассмотрены
переходные
электромеханические
процессы
,
анализ
которых
показал
,
что
предложенное
векторное
управление
позволяет
существенно
сократить
качания
в
энергосистеме
и
колебания
активной
мощности
после
возмущений
.
В
работе
отмечено
,
что
применение
АСЭМПЧ
поз
воляет
на
практике
реализовать
метод
баланса
искажающих
мощностей
для
опреде
–
ления
источников
ухудшения
качества
электрической
энергии
.
Ключевые
слова
:
переходный процесс,
неоднородная сеть,
векторное управление,
асинхронизированная
синхронная машина,
качество электроэнергии
ВВЕДЕНИЕ
При объединении крупных энергосистем (ЭС) возникает проблема регули-
рования значительных по величине перетоков активной мощности, кото-
рые являются следствием различных причин [1–3]. Поскольку развитие от-
дельных участков больших энергосистем может происходить независимо
друг от друга, а техническое перевооружение сетевых организаций может
отставать от роста нагрузки крупных узлов потребления, то в определен-
ный момент силовое оборудование энергосистемы становится неспособ-
ным обеспечить ее надежное функционирование ввиду недостаточной
пропускной способности [1–3, 7–8, 10–13, 19–23]. Ее повышению способ-
ствует применение smart-технологий в энергетике, а в частности, асинхро-
низированный электромеханический преобразователь частоты (АСЭМПЧ)
[3, 7–9, 16, 17].
В силу капиталоемкости АСЭМПЧ, его установка предлагается на су-
ществующей подстанции (ПС) с двумя автотрансформаторами 500/220 кВ
параллельно автотрансформаторам [16, 29].
Характерно, что аналогичные работы ранее уже были предложены. На-
пример, предлагалось использовать токоограничивающий реактор (ТОР)
параллельно с АСЭМПЧ, но только для анализа установившихся режимов
(УР) без учета влияния генераторов на режимы ЭС и уровня напряжения
на статические характеристики нагрузки СХН. В результате, неисследован-
ными остаются вопросы работы АСЭМПЧ в сложнозамкнутых неоднород-
ных ЭС в установившихся режимах и при переходных электромеханиче-
ских процессах (ПП).
Выбор АСЭМПЧ в качестве устройства для создания гибкой связи об-
условлен целым рядом его преимуществ [3, 4, 7, 10, 11, 24]:
– широкий диапазон управления перетоком активной мощности;
– независимое регулирование реактивной мощности и напряжения в двух
узлах подключения;
– обеспечение полной электрической развязки отдельных участков ЭС,
что позволяет исключить протекание токов короткого замыкания (КЗ)
Супрунов
И
.
С
.,
ведущий эксперт ОРЭС
АО «НТЦ ЕЭС Развитие
энергосистем»
Дворкин
Д
.
В
.,
к.т.н., ведущий специалист
ОРЭС АО «НТЦ ЕЭС
Развитие энергосистем»
Новиков
Н
.
Л
.,
д.т.н., профессор НИУ
«МЭИ», в.н.с. ОИВТ РАН,
заместитель Научного
руководителя АО «НТЦ
ФСК ЕЭС»
Новиков
А
.
Н
.,
с.н.с. ФБУ «НТЦ
Энергобезопасность»
85
M
1
M
2
П1
П2
Регулятор
Т1
Т2
Тп1
Тп2
1
U
2
U
АСЭМПЧ
Z
П1
П2
q
q
d
d
Регулятор
в
fd
i
fq
i
л
P
Z
Z
с
U
Ротор
и кондуктивных помех из одного участка в дру-
гой;
– работа в качестве накопителя электрической
энергии (ЭЭ).
МОДЕЛЬ
АСЭМПЧ
В
ОБЩЕМ
ВИДЕ
АСЭМПЧ включает в себя две асинхронизированные
синхронные машины (АСМ), соединенные общим
валом, статорные обмотки, подключенные к трех-
фазной сети (одной или двум, электрически не свя-
занным), преобразователи частоты, систему воз-
буждения, ее регулятор и пр. (рисунок 1) [13, 23, 24,
26–33]. Ротор каждой АСМ имеет две симметрично
расположенные обмотки возбуждения
d
–
d
и
q
–
q
, пита-
ние которых осуществляется от П1 и П2 переменным
током с частотой
.
Частота вращения поля ротора (
) формируется
в зависимости от скорости вращения вала АСЭМПЧ
(
в
) и выбираемой частоты ориентации
ор
, с кото-
рой необходимо обеспечить вращение вектора ЭДС
E
каждой из АСМ
[35]:
=
ор
–
в
.
(1)
В УР частота вращения
E
имеет вид:
E
=
в
+
.
(2)
При подстановке (27) в (1) видно:
E
=
ор
.
(3)
Таким образом, частота вращения ЭДС не зависит
от частоты вращения вала
в
. Частота
ор
принима-
ется равной частоте
той подсистемы
, к которой
подключена машина. Изменением
E
обеспечивает-
ся требуемый режим работы АСЭМПЧ.
Так как магнитный поток ротора образуется как
результирующий двух потоков
d
–
d
и
q
–
q
, создаваемых
токами возбуждения
i
fd
и
i
fq
, то соответствующий ему
ток ротора можно рассматривать как вектор в соб-
ственной системе координат ротора (
d
–
q
); ось
d
со-
впадает с осью обмотки
d
–
d
, а ось
q
— с осью обмотки
q
–
q
. Принимается, что ось
d
— мнимая, а ось
q
— дей-
ствительная. Тогда ток возбуждения определяется
согласно выражению:
İ
f
=
i
fq
+
j
∙
i
fd
.
(4)
В описанных координатах уравнения Парка-Горе-
ва принимают вид:
1
–
u
̇
s
= —
x
s
∙
i
̇
s
+ (
p
+
j
ор
) ∙ (
x
s
∙
i
̇
s
+
e
̇
f
)
T
u
̇
f
=
e
̇
f
+ [
p
+
j
(
ор
–
в
)] ∙ (
∙
x
s
i
̇
s
+
e
̇
f
) ∙
T
f
(5)
T
f
∙
p
в
= –
2
= 1
Re
(
j
∙
e
̇
f
i
̂
s
),
где
u
̇
f
= (
x
af
∙
u
̇
f
в
)/
r
f
— приведенное напряжение воз-
буждения, пропорциональное напряжению
u
̇
f
в
, при-
ложенному к обмоткам возбуждения;
e
̇
f
=
x
af
∙
i
̇
f
—
приведенный ток ротора, пропорциональный току
i
̇
f
;
T
f
=
x
f
/
r
f
— постоянная времени обмотки ротора;
=
x
2
af
/(
x
s
∙
x
f
) — коэффициент магнитной связи между
обмотками статора и ротора;
T
=
x
s
/
r
s
— постоянная
времени обмотки статора.
Регулированием возбуждения АСЭМПЧ обеспе-
чивается гармоническое изменение подводимого
к обмоткам возбуждения напряжения управления
u
̇
f
с частотой
f
[24, 34, 37–40]:
u
̇
f
(ор)
=
u
‘
f
(ор)
+
ju
”
f
(ор)
,
(6)
Изменение модуля и фазы ЭДС
E
̇
обуславлива-
ется изменением напряжения возбуждения
u
̇
f
у
по за-
кону:
u
‘
у
(ор)
=
0
+
W
i
(
p
) ∙
П
i
(7)
i
u
”
у
(ор)
=
0
+
W
j
(
p
) ∙
П
j
,
j
где
u
‘
у
(ор)
и
u
”
у
(ор)
— проекции напряжения управле-
ния на оси
q
ор
и
jd
ор
соответственно;
0
и
0
— па-
раметры установившегося режима;
W
i
(
p
),
W
j
(
p
) —
передаточные функции АРВ АСМ; П
i
, П
j
— пара-
метры УР.
Изменение частоты вращения
f
как функции ча-
стоты
ор
выбранного вектора ориентации и часто-
ты вращения вала преобразователя
в
может быть
определено из условия
обеспечения установивше-
гося режима при частоте
вала
в
, отличной от часто-
ты примыкающей подсисте-
мы
ор
(
f
=
ор
–
в
).
Для увеличения пропуск-
ной способности сети рас-
смотрен случай установки
АСЭМПЧ с включенным па-
раллельно машинам АТ [29,
33]. В целях упрощения ком-
плекс АСЭМПЧ и АТ обо-
значается как устройство
управления перетоком мощ-
ности (УУПМ, рисунок 2).
Далее
рассматривается
УУПМ с АСЭМПЧ 200 МВт
и АТ 500/220 кВ мощностью
500 МВА с комплексным со-
противлением 60 Ом.
Рис
. 1.
Принципиальная
схема
АСЭМПЧ
и
его
системы
управления
№
2 (65) 2021
86
Изменение перетока
P
Л
A
осуществляется путем
регулирования перетока
мощности
управления
АСЭМПЧ
P
у
. При этом
активная мощность, про-
текающая через АТ, опре-
деляется по выражению
[33]:
P
АТ
=
P
Л
A
–
P
у
. (8)
При уменьшении
P
у
в направлении от узла
a
к узлу
b
уменьшается
переток мощности
P
Л
A
по
воздушной линии (ВЛ).
Уменьшение мощности
P
Л
A
по ВЛ происходит и при
изменении направления перетока
P
у
.
РАБОТА
УУПМ
ДЛЯ
УПРАВЛЕНИЯ
ГИБКОЙ
МЕЖСИСТЕМНОЙ
СВЯЗЬЮ
И
УВЕЛИЧЕНИЯ
ЕЕ
ПРОПУСКНОЙ
СПОСОБНОСТИ
Схема исследуемой неоднородной сложнозамкну-
той межсистемной связи представлена на рисунке 3.
В определенных режимах может быть достигнута
перегрузка ВЛ 2 и 3 (220 кВ), в то время как ВЛ 1
(500 кВ) останется недогруженной. Поэтому возни-
кает потребность в управлении перетоком мощности
по ВЛ 220 кВ в зависимости от режима с целью его
ограничения
P
ВЛ220
≤
P
доп
. При рассмотрении принци-
па управления перетоком по ВЛ с помощью УУПМ
вводится допущение, что расхождение векторов на-
пряжений
U
A
и
U
B
по концам ВЛ в узлах
A
и
B
электри-
ческой сети энергосистемы постоянно (рисунок 4), то
есть [33]:
AB
=
Aa
+
ab
+
bB
=
Const
.
(9)
В силу численной малости величин активных
сопротивлений участков электропередачи и прини-
мая в качестве допущения, что модули напряжений
в узлах
a
и
b
остаются неизменными за счет регу-
лирования выдачи реактивной мощности АСМ, спра-
ведливо, что активная мощность
P
Л
A
и
P
Л
b
(рисунок 2)
определяется векторами напряжений
U
A
и
U
a
,
U
b
и
U
B
:
P
Л
A
=
P
A
max
sin
(
Aa
–
Aa
),
(10)
P
Л
b
=
P
b
max
sin
(
bB
–
bB
),
(11)
где
P
A
max
,
P
b
max
— амплитудные значения активных
мощностей, протекающих на участках A
A
–
a
и
b
–
B
.
В границах принятых обозначений: активная
мощность, протекающая через АТ, определяется по
выражению:
P
АТ
=
U
a
U
b
sin
ab
/
x
АТ
,
(12)
Т1
Т2
АТ
A
B
ВЛ
ВЛ
АТ
P
АС ЭМПЧ
у
P
у
P
A
Л
P
УУПМ
a
b
b
Л
P
Рис
. 2.
Структурная
схема
управляемой
ВЛ
с
УУПМ
Рис
. 3.
Электрическая
схема
исследуемой
сети
с
комбинированным
устройством
Рис
. 4.
Векторная
диа
–
грамма
напряжений
ВЛ
рассматриваемой
элек
–
тропередачи
у
P
ПС 1
ПС 2
ПС 3
3
3′
ПС 4
ПС 5
Н
Н
Н
Н
Н
Н
Н
ВЛ1
ВЛ2
ВЛ3
ВЛ4
ВЛ5
ВЛ6
ВЛ7
ЭЭС1
ЭЭС2
сеч
P
1
ВЛ
P
ВЛ8
2
ВЛ
P
3
ВЛ
P
ПС 6
ПС 7
500 кВ
500 кВ
220 кВ
220 кВ
220 кВ
220 кВ
220 кВ
220 кВ
у
P
Т1
Т2
АТ
P
АС
ЭМПЧ
УУПМ
AB
Aa
ab
bB
.
A
U
.
a
U
.
b
U
.
B
U
G
G
G
G
КАЧЕСТВО
ЭЛЕКТРОЭНЕРГИИ
87
из которого видно, что угол сдвига между напряже-
ниями
U
a
и
U
b
x
АТ
P
АТ
ab
=
arcsin
—.
(13)
U
a
U
b
Анализ выражений (10)–(12) показывает, что при
P
у
> 0 с уменьшением этой мощности, мощность
P
АТ
и угол
ab
. Тогда, согласно (9), величины углов
Aa
и
bB
уменьшаются, активная мощность на участках
электропередачи
P
Л
A
и
P
Л
b
тоже уменьшаются. Наобо-
рот, при увеличении мощности
P
у
> 0 значения опи-
санных величин увеличиваются.
Увеличение перетока активной мощности в сече-
нии вызывает снижение напряжения и, в свою оче-
редь, увеличение перетока реактивной мощности,
что приводит к росту токовой загрузки ВЛ 2 выше
допустимой. На рисунке 5 показана угловая характе-
ристика работы комбинированного устройства с уче-
том режимных ограничений. До значения перетока
активной мощности 200 МВт режимные ограниче-
ния не требуются. В точке 1 вводится ограничение
мощности вплоть до точки 2, определяемое необ-
ходимостью поддержания этого значения мощно-
сти по условию балансовой ситуации
в электроэнергетической системе. На
участке 2–3 происходит превышение
длительно допустимого тока ВЛ 2, вы-
званное ростом перетока реактивной
мощности по ней. При этом необходи-
мо уменьшать передаваемую актив-
ную мощность ниже
P
ВЛ2_доп
. При даль-
нейшем увеличении передаваемой
мощности происходит недопустимое
снижение напряжения на подстанциях
прилегающей сети. Для недопущения
снижения напряжения переток мощно-
сти по ВЛ 2 необходимо дополнитель-
но снижать. Прирост передаваемой по
сети активной мощности снижается
вплоть до нуля, после чего максималь-
ный допустимый переток в сечении
продолжает снижаться.
Управление в рамках логики (10)–(27) с помощью
УУПМ позволяет повлиять на потокораспределение,
разгрузив слабые участки электропередачи. При
этом данный алгоритм работоспособен, как на при-
мере упрощенной сети (рисунок 2), так и на примере
сложнозамкнутой ЭС (рисунок 3).
ФОРМИРОВАНИЕ
МАТЕМАТИЧЕСКОЙ
МОДЕЛИ
СЛОЖНОЙ
ЭС
ПРОИЗВОЛЬНОЙ
СТРУКТУРЫ
ДЛЯ
РАСЧЕТА
ПП
C
УУПМ
На рисунке 6 представлена принципиальная схема
сложнозамкнутой неоднородной ЭС, которая ис-
пользовалась для расчета электромеханических ПП.
Электрическая сеть состоит из трансформаторов,
АТ, ВЛ и нагрузок. Уравнения для этих элементов за-
писываются в системе координат
d
и
q
опорной ма-
шины. Система уравнений, описывающая каждую
АСМ в осях
d
и
q
[17, 24, 30, 35], принимает вид:
U
d
=
s
(
E
d
+
i
q
∙
x
q
),
(14)
U
q
=
s
(
E
q
+
i
d
∙
x
d
),
(15)
p
∙
E
‘
d
= (
E
de
–
E
d
) /
T
q
0э
–
s
∙
E
‘
q
,
(16)
Рис
. 5.
Угловые
характеристики
мощности
исследуемой
связи
с
учетом
управления
перетоком
мощности
по
ВЛ
2 (
ограничение
P
ВЛ
2
= 200
МВт
)
МВт
1600
1400
1200
1000
800
600
400
200
0
0
10
20
5
15
25
30
P
сеч
P
ВЛ2
1
2
3
Г1
Г3
Н
Н
Н
в
М1
М2
Т1
Т2
Регулятор
AT
Г2
Г4
Н
500 кВ
220 кВ
500 кВ
220 кВ
3
К
1
3
2
4
5
6
7
8
P
Z
Рис
. 6.
Схема
исследуемой
ЭЭС
(
стрелкой
указано
направление
перетока
активной
мощности
УУПМ
в
исходном
установившемся
режиме
)
№
2 (65) 2021
88
W
p k
W
p k
e
i
E
W
p k
W
p k
U
1
1 +
( )·
( )·
( )·
( )·
U
pT
+
–
0
U
0
qe
E
1
1
e
T p
уq
V
1
1
e
T p
уd
V
вала
1
1 +
в
pT
–
вала жел
+
g
P
1
P
pT
–
g
жел
P
+
0
de
E
Z
6
0
U
k
0
k
1
1
1
1 +
pT
2
2
1
1 +
pT
+
+
0,5
+
–
0
P
k
0
отк
k
fк
fd
d
e
i
E
qe
E
f
k
+ 1
≈
≈
≈
≈
f
k
f
k
+
+
–
–
f
k
de
E
1
1
U
U
1
1
P
P
1
1
1
1
отк
отк
fк
fq
q
+
+ 1
+
1 +
Z
Z
Z
Z
Z
Z
Z
Z
Z
p
∙
E
‘
q
= (
E
qe
–
E
q
) /
T
d
0э
–
s
∙
E
‘
d
,
(17)
ps
= (
P
эл
–
P
Т
) /
T
j
,
(18)
где
U
d
и
U
q
— напряжения в узле примыкания АСМ;
s
— скольжение вала АСЭМПЧ относительно син-
хронной скорости;
s
— синхронная скорость вра-
щения электрической сети;
E
‘
d
и
E
‘
q
— переходные
ЭДС;
E
d
и
E
q
— ЭДС холостого хода;
i
d
и
i
q
— ток ста-
тора АСМ;
x
d
и
x
q
— синхронные индуктивные со-
противления АСМ (вводится допущение о магнитной
симметрии ротора АСМ);
P
эл
и
P
Т
— электрическая
мощность машины, отдаваемая в сеть, и механиче-
ская мощность на валу машины;
T
d
0э
и
T
q
0э
— эквива-
лентные постоянные времени контуров ротора;
T
j
—
постоянная инерции ротора АСМ.
АСМ Г7 и Г8 оснащены АРВ СД. Регулирование
возбуждения производится по отклонению напряже-
ния на зажимах генератора от заданного значения
и его производной по времени, отклонению скольже-
ния вала АС ЭМПЧ от заданного значения и его произ-
водной по времени, а также по отклонению мощности
управления
P
у
от заданного значения (рисунок 7) [24].
Вектор вынужденной ЭДС,
E
e
, раскладывается
в синхронных осях. Угол
e
— это сдвиг роторов гене-
раторов подсистемы относительно синхронной оси,
который определяется по формуле:
N
i
= 1
T
Ji
∙
i
e
= —,
(19)
N
i
= 1
T
Ji
где
N
— число генераторов в подсистеме;
T
Ji
— по-
стоянная инерции
i
-го генератора;
i
— угол сдвига
ротора
i
-го генератора относительно синхронной оси.
Если разложение ЭДС холостого хода
E
, в син-
хронных координатах имеет значение
E
q
и
E
d
, то в ко-
ординатах подсистемы
, к которой подключена АСМ,
оно меняется на
E
q
и
E
d
соответственно (рисунок 8).
Рис
. 8.
Разложение
вектора
вынужденной
ЭДС
(
а
)
и
ЭДС
холостого
хода
(
б
)
в
синхронных
осях
с
q
с
d
1
q
1
d
e
E
qe
E
de
E
e
с
q
с
d
d
E
q
E
d
E
e
q
E
d
E
q
G
G
[
[
а)
б)
КАЧЕСТВО
ЭЛЕКТРОЭНЕРГИИ
Рис
. 7.
Структурная
схема
АРВ
АСМ
в
составе
АС
ЭМПЧ
в
общем
виде
89
Из рисунка 8 справедливы следующие соотноше-
ния (отдельно для каждой подсистемы) [25, 39]:
E
q
=
E
q
cos
(
e
) +
E
d
sin
(
e
)
(20)
E
d
= –
E
q
sin
(
e
) +
E
d
cos
(
e
).
Закон регулирования возбуждения АСМ в общем
виде:
V
у
d
=
E
d
0
+
V
s
(
s
) +
V
P
(
P
),
(21)
V
у
q
=
E
q
0
+
V
U
(
U
),
(22)
где
V
s
— закон управления по отклонению скольже-
ния вала;
s
— величина отклонения скольжения
вала
s
;
V
P
— закон управления по отклонению пере-
даваемой мощности;
P
— величина отклонения
передаваемой мощности
P
;
V
U
— закон управления
по отклонению напряжения на выводах комбини-
рованного устройства;
U
— величина отклонения
напряжения
U
;
V
у
d
и
V
у
q
— проекции напряжения
возбуждения АСМ;
E
d
0
и
E
q
0
— начальные значе-
ния ЭДС холостого хода АСМ.
Используя (20)–(22), проводится обратный пере-
ход к синхронным осям:
E
qe
= (1 +
k
f
)(
V
у
q
cos
(
e
) –
V
у
d
sin
(
e
)) –
k
f
E
d
(23)
E
de
= (1 +
k
f
)(
V
у
q
sin
(
e
) –
V
у
d
cos
(
e
)) –
k
f
E
q
,
где
k
f
— коэффициент обратной связи по току ротора
АСМ.
РАСЧЕТ
ПП
В
ЭНЕРГОСИСТЕМЕ
БЕЗ
УЧЕТА
И
С
УЧЕТОМ
УСТАНОВКИ
КОМБИНИРОВАННОГО
УСТРОЙСТВА
УПРАВЛЕНИЯ
ПЕРЕТОКОМ
АКТИВНОЙ
МОЩНОСТИ
При рассмотрении ПП использовалась схема,
представленная на рисунке 6. Было рассмотрено
трехфазное КЗ на ВЛ 500 кВ в дефицитной части
ЭС (подсистема 1) длительностью 0,3 секунды
в узле 7. Установка УУПМ существенно снижает
влияние на избыточную часть ЭС (разница харак-
терных величин достигает 25%). В дефицитной ча-
сти ЭС УУПМ позволяет значительно снизить ам-
плитуду качаний роторов генераторов.
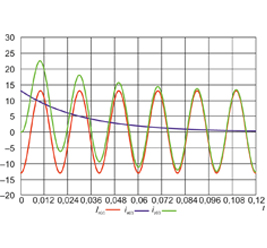
Анализ графиков ПП без и с УУПМ показал,
что его установка позволяет снизить влияние вза-
имных качаний генераторов двух подсистем (ри-
сунок 9). В результате, УУПМ повышает устойчи-
вость генераторов, демпфирует слабозатухающие
колебания и уменьшает длительность ПП.
Дополнительный интерес представляет работа
ЭС с УУПМ при питании части нагрузки непосред-
ственно от него (после ликвидации КЗ). В этом ре-
жиме АСЭМПЧ поддерживает заданные значения
напряжения на своих шинах
U
, и передаваемой
активной мощности,
P
уст
. Напряжение возбуждения
формируется в виде:
E
de
1
=
E
de
01
+
k
0
1
∙ (
в
–
в жел1
) +
k
0
1
отк
∙
отк
, (24)
E
de
2
=
E
de
02
+
k
0
P
∙ (
P
g
–
P
уст
) +
k
0
2
отк
∙
отк
, (25)
где
в
=
s
в
+ 1 и
в жел1
= (
1
+
2
)/2 — фактическая
и желаемая скорость вращения вала;
отк
=
1
–
2
—
разница частот двух подсистем;
k
0
1
отк
и
k
0
2
отк
— ко-
эффициенты усиления по разнице частот в разде-
ленных частях ЭС;
0
1
,
k
0
2
и
k
0
P
— коэффициенты
усиления по отклонению частот в разделенных час-
тях ЭС и по отклонению передаваемой активной
мощности;
P
g
— передаваемая активная мощность.
Отключение ВЛ ведет к изменению режима ра-
боты УУПМ с поддержания заданной передаваемой
мощности на поддержание номинальной частоты
в прилегающей сети.
d
в1
E
de
1
=
E
de
01
+
k
0
1
(
в1
–
жел1
) +
k
0
1
отк
∙
отк
+
k
Д
1
—, (26)
dt
d
в2
E
de
2
=
E
de
02
+
k
0
2
(
в2
–
жел2
) +
k
0
2
отк
∙
отк
+
k
Д
2
—, (27)
dt
где
k
Д
1
и
k
Д
2
— коэффициенты усиления по произво-
дной изменения скорости вращения вала АСЭМПЧ
для подсистем 1 и 2.
При выводе в ремонт АТ после КЗ на ВЛ 6–7 пере-
дача электрической мощности УУПМ осуществляет-
ся только машинами АСМ (отключение в единичной
ремонтной схеме).
В исходном режиме первая АСМ, подключенная
к узлу 6, работает в двигательном режиме и потреб-
ляет активную мощность. Вторая АСМ работает в ге-
нераторном режиме и выдает активную мощность
в узле 5.
В результате ликвидации КЗ на ВЛ 6–7 нагрузка
в узле 6 схемы не отключается и ее электроснабже-
ние осуществляется от АСЭМПЧ. При этом проис-
ходит автоматический реверс АСМ: 1-я переходит
в генераторный режим, а 2-я — в двигательный (ри-
сунок 10).
0,015
0,02
0,025
0,03
0,035
0,04
0,045
0,05
0,055
0,06
0
1
2
3
4
5
У
го
л
ро
тора,
о.е.
t
, сек
с АСЭМПЧ
без АСЭМПЧ
Рис
. 9.
Угол
ротора
генератора
Г
2 (
а
)
и
Г
3 (
б
)
а)
б)
0,06
0,08
0,1
0,12
0,14
0,16
0
1
2
3
4
5
У
го
л
ро
тора,
о.е.
t
, сек
без АСЭМПЧ
с АСЭМПЧ
№
2 (65) 2021
90
Реверс АСМ осуществляется за 3 секунды, при
этом за 0,4 секунды возобновляется электроснабже-
ние потребителей со стороны 1-й машины, при этом
частота в примыкающей сети поддерживается в до-
пустимых пределах. Таким образом, проведенные
эксперименты показывают высокую эффективность
УУПМ в задаче качественного улучшения условий
протекания ПП и позволяют сформировать алгоритм
управления АСЭМПЧ в случае его выделения на
сбалансированную ЭС.
ОПРЕДЕЛЕНИЕ
ИСТОЧНИКОВ
ИСКАЖЕНИЯ
СИНУСОИДАЛЬНОСТИ
И
СИММЕТРИИ
НАПРЯЖЕНИЯ
С
ПОМОЩЬЮ
АСЭМПЧ
Поскольку мощность АСМ АСЭМПЧ достаточно вели-
ка, УУПМ способно длительное время питать крупных
потребителей участка ЭС, выделенного на изолиро-
ванную работу, не только после ликвидации КЗ, как
было показано ранее, но и в нормальных режимах ра-
боты. Это открывает дополнительную возможность по
выявлению источников искажений синусоидальности
и симметрии напряжения в ЭС. Пусть потребители
АТ УУПМ выделены на односторонне питание от 1-й
АСМ. (АТ отключен со стороны СН). Тогда, на частоте
рассматриваемого искажения (гармоники или после-
довательности), изолированный
район описывается эквивалент-
ной схемой Тевенина на рисун-
ке 11. В этой схеме потребитель,
работа которого не ухудшает ка-
чества электрической энергии
(КЭЭ), представлен пассивной
ветвью с некоторым эквивалент-
ным сопротивлением. Напротив,
если потребитель является нели-
нейным или несимметричным, то
его ветвь на частоте рассматри-
ваемого искажения активная и со-
держит эквивалентную ЭДС.
Особенность данной схемы —
электрическая близость шины
НН АТ и узлов 5 и 6, так как:
11
2
— ∙
Z
̇ ‘
АТ
Z
̇
АТ
k
АТ ВН–НН
∙
Z
̇ ‘
АТ
500
2
Z
̇ ‘
АТ
— = — = — = 4,84 ∙ 10
-4
—, (28)
Z
̇
эк
Z
̇
эк
Z
̇
эк
Z
̇
эк
где
Z
‘
АТ
— сопротивление АТ, приведенное к сторо-
не ВН;
k
АТ ВН-НН
— коэффициент трансформации АТ
между сторонами ВН и НН;
Z
эк
— эквивалентное со-
противление нагрузки АТ.
Направление протекания токов искажений в ак-
тивных ветвях схемы условны и определяются сло-
жившимся режимом работы. До выделения участка
сети на изолированную работу (питание от узлов 5
и 6 схемы) значение тока рассматриваемого иска-
жения в каждой
j
-й ветви схемы и его направление
определяется соотношением величин эквивалент-
ного ЭДС ветви и напряжения на стороне НН АТ,
через коэффициент пропорциональности — экви-
валентное сопротивление ветви:
I
̇
j
= (
U
̇
НН
–
E
̇
j
) /
Z
̇
j
.
(29)
В зависимости от сложившегося режима работы
направление тока в активных ветвях может быть
различным: от шин НН (условно положительное на-
правление), когда искажающий потребитель не яв-
ляется доминирующим; или к шинам НН (условно
отрицательное направление), когда искажающий по-
требитель является доминирующим. При этом в пас-
сивных ветвях схемы направление токов от шин НН
неизменно (
E
1
и
E
2
равны нулю).
При выделении участка сети на изолированную
работу (питание только от узла 6) справедливо
утверж дение о симметрии и синусоидальности на-
пряжения в узле 6, что обеспечивается 1-й АСМ.
В этих условиях с учетом (28) справедливо до-
пустить, что напряжение на стороне НН АТ также
всегда практически симметрично и синусоидаль-
но. В таком случае на частотах рассматриваемых
искажений напряжение по стороне НН АТ стремит-
ся к нулю (но не достигает его), а выражение (29)
принимает вид:
I
̇
j
≈ –
E
̇
j
/
Z
̇
j
,
(30)
где знак минуса в числителе говорит, что при выде-
лении участка сети на изолированную работу ток на
частоте искажения в активной ветви потребителя
всегда направлен к шинам НН.
КАЧЕСТВО
ЭЛЕКТРОЭНЕРГИИ
-0,07
-0,05
-0,03
-0,01
0,01
0,03
0,05
0,07
0
1
2
3
4
5
Электрическая мощность, о.е.
t
, сек
Г7
Г6
1
2
3
4
Рис
. 10.
Электрическая
мощность
Г
6
и
Г
7
Рис
. 11.
Эквивалентная
схема
Тевенина
изолированного
района
на
частоте
рассматриваемого
искажения
:
Z
АТ
—
эквивалентное
сопротивление
АТ
,
приведенное
к
сто
–
роне
НН
;
Z
j
—
сопротивление
ветви
j
–
го
потребителя
;
E
j
—
ЭДС
на
частоте
рассматриваемого
искажения
,
обусловленное
работой
j
–
го
потребителя
91
В свою очередь, ток в пассивных ветвях неиска-
жающих потребителей всегда направлен от шин НН
и определяется по выражению (на примере ветви
с индексом 1):
I
̇
1
=
E
̇
j
Z
̇
j
/ (
Z
̇ ‘
j
Z
̇
1
),
(31)
где
Z
̇ ‘
j
— входное сопротивление
j
-й ЭДС.
Иными словами, в момент выделения участка
сети на изолированную нагрузку токи искажений во
всех активных ветвях поменяют направление к ши-
нам НН (если до этого имели направление от шин
НН). Таким образом, АСЭМПЧ позволяет на практике
определить с очень высокой точностью искажающую
нагрузку по аналогии с методом баланса искажаю-
щих мощностей, неоднократно описанном в литера-
туре [41, 42].
Частный случай — ситуация, когда ЭДС
j
-й ветви
электрически близка к шинам НН (
Z
j
≈ 0). В сложив-
шейся ситуации выделение участка сети на изоли-
рованную работу не приведет к изменению значения
тока в этой ветви и напряжения искажения на сторо-
не НН. Но в этом случае, по описанным критериям,
будет определен доминирующий источник искаже-
ния КЭЭ в сети.
Следует отметить, представленная на рисунке 6
схема позволяет последовательно провести выделе-
ние разных участков сети на изолированную работу
с помощью АСЭМПЧ, то есть аналогичным образом
определить источники искажения КЭЭ в них. При
этом (потенциально) выделение участков сети огра-
ничено двумя факторами:
– в настоящий момент не исследован вопрос дли-
тельной работы АСЭМПЧ на несинусоидальную
и несимметричную нагрузку. Это может оказаться
важным фактором, поскольку измерение угла
между вектором напряжения и синхронной осью
q
(для корректной работы системы возбуждения
АСМ) может проводиться с некоторой погрешно-
стью в условиях протекания несинусоидальных
и несимметричных токов (при отборе телеизмере-
ний на шинах ВН генераторного трансформатора);
– поскольку АСЭМПЧ представляет собой стацио –
нарное устройство без возможности его пере-
мещения, выделение участков сети на изолирован-
ную работу в значительной степени зависит от схе-
мы подключения примыкающих энергорайонов.
ВЫВОДЫ
1. Представлена математическая модель АСЭМПЧ
на базе двух АСМ, соединенных единым валом,
и сформулированы основные преимущества вне-
дрения этой системы для управления УР и ПП
в ЭС.
2. Разработан принцип управления работой
АСЭМПЧ с целью влияния на потокораспределе-
ние в системе на примере сложнозамкнутой не-
однородной сети.
3. Отражены аспекты внедрения АСЭМПЧ парал-
лельно с АТ 500/220 кВ в составе комбинирован-
ного устройства управления перетоком мощности
(УУМП).
4. Предложена векторная система управления
и разработаны алгоритмы управления УУПМ для
обеспечения работы гибкой межсистемной связи
в УР и ПП.
5. Показан принцип управления УУПМ для увеличе-
ния пропускной способности межсистемной связи.
6. Проведена оценка эффективности применения
УУПМ для повышения пропускной способности
межсистемной связи на основании расчета УР на
математической модели сложной ЭС.
7. Определены законы управления УУПМ для обес-
печения динамической устойчивости на основа-
нии расчетов ПП. Показано, что разработанные
алгоритмы управления УУПМ в различных режи-
мах его работы позволяют повысить пропускную
способность ЭС в УР, снизить время протекания
ПП и обеспечить электроснабжение при выделе-
нии части нагрузки на одностороннее питание.
8. Определены условия, при которых УУПМ позво-
ляет повысить КЭЭ выделенного на изолирован-
ную работу участка сети и показана методика
применения АСЭМПЧ для определения потреби-
телей в этом участке, вносящих основной вклад
в ухудшение КЭЭ методом баланса искажающих
мощностей.
ЛИТЕРАТУРА
1. Дорофеев В.В., Макаров А.А. Ак-
тивно-адаптивная сеть — новое
качество ЕЭС России // Энергоэк-
сперт, 2009, № 4. С. 28–34.
2. Шакарян Ю.Г., Новиков Н.Л. Тех-
нологическая платформа SMART
GRID (основные средства) // Энер-
гоэксперт, 2009, № 4. С. 42–49.
3. Шакарян Ю.Г., Новиков Н.Л., Нови-
ков А.Н. Устройства управляемых
(гибких) систем электропередачи
переменного тока (FACTS) и ре-
комендации по их применению
в электроэнергетических системах
России // Электрические станции,
2018, № 9. С. 20–36.
4. Супрунов И.С., Лихачев А.П., Двор-
кин Д.В. Внедрение АСЭМПЧ для
ограничения токов короткого за-
мыкания на примере мегаполиса /
Сборник работ лауреатов между-
народного конкурса научных, на-
учно-технических и инновацион-
ных разработок, направленных на
развитие топливно-энергетической
и добывающей отрасли. М.: Мини-
стерство энергетики Российской
Федерации, ООО «Технологии раз-
вития», 2020, С. 36–41.
5. Дементьев Ю.А., Сокур П.В., Ша-
карян Ю.Г. и др. Электромеханиче-
ская вставка переменного тока для
управления режимами и ограни-
чения токов короткого замыкания
// Энергия единой сети, 2017, №4
(33), С. 18–27.
6. Волков Э.П., Баринов В.А. О соз-
дании электрической связи 220 кВ
между ОЭС Сибири и ОЭС Востока
// Энергетик, 2008, № 5, С. 2–8.
7. Зеленохат Н.И., Шаров Ю.В. Но-
вые технологические решения про-
блемы осуществления совместной
работы энергообъединений Восто-
ка и Запада // Электричество, 2007,
№ 9. С. 34–40.
8. Зеленохат Н.И., Шаров Ю.В. Ком-
бинированное объединение боль-
ших энегросистем // Электриче-
ство, 2006, № 5. С. 2–10.
9. Зеленохат Н.И., Шаров Ю.В., Дени-
сов Д.И. Квазиуправляемые межго-
сударственные электрические свя-
зи и их режимные свойства // Новое
№
2 (65) 2021
92
в Российской электроэнергетике,
2005, №10, С. 4–12.
10. Шакарян Ю.Г. Управляемые (гиб-
кие) системы передачи перемен-
ного тока. URL: http://fsk-ees.ru/
common/img/uploaded/managed_
systems.pdf.
11. Зеленохат Н.И., Власова Т.А. Меж-
системная связь с управляемыми
режимными
характеристиками.
Уч. пос. по курсу «Эксплуатация
электроэнергетических
систем»
по напр. «Электроэнергетика». М.:
Изд-во МЭИ, 2003, 48 с.
12. Бурман А.П., Розанов Ю.К., Шака-
рян Ю.Г. Перспективы применения
в ЕЭС России гибких (управляе-
мых) систем передачи перемен-
ного тока // Электротехника, 2004,
№ 8. С. 30–37.
13. Дорофеев В.В., Шакарян Ю.Г., Коч-
кин В.И. [и др.] Перспективы приме-
нения в ЕЭС России гибких (управ-
ляемых) систем электропередачи
переменного тока // Электрические
станции, 2004, № 8. С. 10–13.
14. Шакарян Ю.Г., Лабунец И.А., Со-
кур П.В. [и др.] Разработка и пер-
спективы применения новых типов
турбогенераторов с векторной сис-
темой управления возбуждением //
Электротехника, 2010, № 2. С. 4–9.
15. Дьяков А.Ф., Зеленохат Н.И. Но-
вые подходы к решению проблемы
совместной работы ЕЭС России
с энергосистемами других стран //
Известия Академии электротехни-
ческих наук РФ, № 2, 2009. С. 1–10.
16. Зеленохат О.Н. [и др.] Управление
перетоками мощности по межсис-
темным связям в стационарных
режимах с применением новых
технологий // Энергетик, 2012, № 6.
С. 43–45.
17. Зеленохат Н.И. Статическая устой-
чивость гибкой межсистемной
связи // Вестник МЭИ, 1996, № 4.
С. 32–38.
18. Зеленохат Н.И. Анализ режимных
характеристик межсистемной свя-
зи со статическими компенсато-
рами // Электричество, 1997, № 3.
С. 13–18.
19. Kirschner L., Retzmann D., Thumm
G. Benefi ts of FACTS for Power Sys-
tem Enhancement. IEEE/PES Trans-
mission and Distribution Conference
and Exhibition: Asia and Pacifi c 2005,
pp. 88-98.
20. Paserba J. How FACTS Controllers
Benefi t AC Transmission Systems
// IEEE PES General Meeting Panel
Session on FACTS Fundamentals.
Denver, Colorado, 2004, pp. 320-
325.
21. Baldick R., Kahn E. Contract paths,
phase shifters, and effi cient elec-
tricity trade. IEEE Transaction on
Power Systems, 1999, vol. 12, no. 2,
pp. 749-755.
22. Sood V.K. HVDC and FACTS Control-
lers. Applications of Static Converters
in Power Systems. Boston: Kluwer
Academic Publishers, 2004, 245 р.
23. Кочкин В.И., Шакарян Ю.Г. Режи-
мы работы управляемых линий
электропередачи // Электричество,
1997, № 9, С. 2–8.
24. Зеленохат Н.И. Повышение эф-
фективности управления режи-
мами гибкой межсистемной связи
с ЭВПТ // Вестник МЭИ, 2005, № 3.
С. 66–73.
25. Зеленохат Н.И. Проблема обмена
электроэнергией между энерго-
объединениями Востока и Запа-
да и принцип комбинированного
подхода к ее решению // Электро,
2004, № 2. С. 2–5.
26. Веников В.А., Зеленохат Н.И. и др.
О применении электромеханиче-
ских преобразователей частоты
в энергосистемах // Электричество,
1977, № 4. С. 10–14.
27. Venikov V.A. [at al.] Application of Dig-
ital Computers to the Study of Power
Systems with Asynchronized Electro-
mechanical Frequency Converters.
New-York: Electrical Power & Power
Systems, vol. 1, no. 2, pp. 113-117.
28. Zelenokhat N.I., Makeyechev V.A.,
Vlasova T.A. Dynamic Characteristics
of Electromagnetically Sectionalized
Electrical Station. CIGRE, Sympo-
sium, London, June 1999.
29. Зеленохат Н.И. Проблема созда-
ния управляемых межсистемных
связей с АСЭМПЧ // Вестник МЭИ,
1995, № 4. С. 97–100.
30. Зеленохат Н.И. Повышение эф-
фективности управления гибкой
межсистемной связи с ЭВПТ //
Вестник МЭИ, 2005, № 3. С. 66–73.
31. Зеленохат Н.И., Зеленохат О.Н.,
Аристов И.С., Микрюков Д.Ю. Ана-
лиз статической устойчивости меж-
системной связи с устройством
управления перетоком мощности //
Энергетик, 2012, № 6. С. 43–45.
32. Глебов И.А., Суханов Л.А., Сафи-
уллина Р.Х. Электромеханические
преобразователи частоты для свя-
зи электроэнергетических систем
// Известия АН СССР. Энергетика
и транспорт, 1977, № 6. С. 49–57.
33. Зеленохат Н.И. Интеллектуализа-
ция ЕЭС России: инновационные
предложения: практическое посо-
бие. М.: Издательский дом МЭИ,
2013. 192 с.
34. Кочкин В.И., Шакарян Ю.Г. Приме-
нение гибких (управляемых) сис-
тем электропередачи переменного
тока в энергосистемах. М.: Торус
пресс, 2011. 311 с.
35. Шакарян Ю.Г. Асинхронизиро-
ванные синхронные машины. М.:
Энергоатомиздат, 1984. 193 с.
36. Меркурьев Г.В., Шаргин Ю.М.
Устойчивость энергосистем. Расче-
ты. СПб.: НОУ «Центр подготовки
кадров энергетики», 2006. 300 с.
37. Ежков В.В., Зеленохват Н.И., Лит-
кенс И.В. и др. Переходные про-
цессы электрических систем в при-
мерах и иллюстрациях. Учеб. посо-
бие для вузов. под ред. В.А. Строе-
ва. М.: Знак, 1996, 224 с.
38. Неуймин В., Иванов В. [и др.]
RUSTAB: руководство пользовате-
ля. TechSystem Group, 2009. 93 с.
39. Мамиконянц Л.Г. Анализ некоторых
аспектов переходных и асинхрон-
ных режимов синхронных и асин-
хронных машин. Под. ред. Ю.Г. Ша-
каряна. М.: ЭЛЕКС-КМ, 2006. 368 с.
40. Peter Van Meirhaeghe. Double fed
induction machine: a EUROSTAG
model // Tractebel Engineering. 2004.
41. Башкиров О.В., Першенков П.П.,
Тюрин Е.А. Определение вклада
потребителя в изменение показа-
телей качества электроэнергии //
Труды международного симпозиу-
ма «Надежность и качество», 2009,
т. 2. С. 77–79.
42. Дворкин Д.В., Силаев М.А., Туль-
ский В.Н., Палис Ш. Проблемы
оценки вклада потребителя в ис-
кажение качества электрической
энергии // Электричество, 2017,
№ 7. С. 12–19.
REFERENCES
1. Dorofeev V.V., Makarov A.A. Active-
adaptive network is a new quality of
UES of Russia // Power Expert, 2009,
no. 4, pp. 28–34. (In Russian)
2. Shakaryan Yu.G., Novikov N.L. IT
platform SMART GRID (basic fea-
tures) // Power Expert, 2009, no. 4,
pp. 42–49. (In Russian)
3. Shakaryan Yu.G., Novikov N.L.,
Novikov A.N. Flexible AC transmis-
sion system (FACTS) devices and
recommendations on their application
in power systems of Russia // Electric
stations, 2018, no. 9, pp. 20–36. (In
Russian)
4. Suprunov I.S., Likhachev A.P., Dvor-
kin D.V. Introduction of asynchronous
electromechanical frequency con-
verter to restrict short circuit currents
by the example of a metropolis / Proc.
of prize winners of the international
competition of research, research &
technical and innovative inventions in-
tended for development of fuel-power
and mining fi elds. Moscow, Ministry
of Energy of the Russian Federation,
КАЧЕСТВО
ЭЛЕКТРОЭНЕРГИИ
93
Tekhnologii razvitiya, OOO, 2020, pp.
36–41. (In Russian)
5. Dement’yev Yu.A., Sokur P.V., Sha-
karyan Yu.G. and others. Electrome-
chanical AC link for operating mode
control and short circuit current re-
striction // Energy of the unifi ed grid,
2017, no. 4 (33), pp. 18–27. (In Rus-
sian)
6. Volkov E.P., Barinov V.A. On estab-
lishment of a 220 kV interconnection
between UPS of Siberia and UPS of
the East // Power Engineer, 2008, no.
5, pp. 2–8. (In Russian)
7. Zelenokhat N.I., Sharov Yu.V. New
technological solutions of coopera-
tion between electric energy associa-
tions of the East and the West // Ele-
ktrichestvo [Electricity], 2007, no. 9,
pp. 34–40. (In Russian)
8. Zelenokhat N.I., Sharov Yu.V. Com-
bined association of large energy
systems // Elektrichestvo [Electricity],
2006, no. 5, pp. 2–10. (In Russian)
9. Zelenokhat N.I., Sharov Yu.V. Den-
isov D.I. Quazi-controllable interstate
electrical connections and their pro-
cess fl ow features // Novoye v Ros-
siyskoy elektroenergetike [New in
Russian power engineering], 2005,
no. 10, pp. 4–12. (In Russian)
10. Shakaryan Yu.G. Controllable (fl ex-
ible) AC transmission systems. URL:
http://fsk-ees.ru/common/img/upload-
ed/managed_ systems.pdf.
11. Zelenokhat N.I., Vlasova T.A. System
interconnection with controllable pro-
cess fl ow characteristics. Study guide
for the course “Electric energy system
operation”, “Power engineering” fi eld.
Moscow, MPEI Publ., 2003, 48 p. (In
Russian)
12. Burman A.P., Rozanov Yu.K., Sha-
karyan Yu.G. Prospects of FACTS
application in UES of Russia // Elec-
tric Engineering, 2004, no. 8, pp. 30–
37. (In Russian)
13. Dorofeev V.V., Shakaryan Yu.G.,
Kochkin V.I. and others. Prospects
of FACTS application in UES of Rus-
sia // Electric stations, 2004, no. 8,
pp. 10–13. (In Russian)
14. Shakaryan Yu.G., Labunets I.A.,
Sokur P.V. and others. Development
and prospects of using new types of
turbogenerators with the phasor sys-
tem of excitation control // Electric
Engineering, 2010, no. 2, pp. 4–9. (In
Russian)
15. D’yakov A.F., Zelenokhat N.I. New
approaches in establishing coopera-
tion of UES of Russia with power sys-
tems of other countries // News of the
Academy of Electrotechnical Scienc-
es of the Russian Federation, no. 2,
2009, pp. 1–10. (In Russian)
16. Zelenokhat O.N. and others. Inter-
connection fl ows control in stationary
operating modes by using new tech-
nologies // Power Engineer, 2012,
no. 6, pp. 43–45. (In Russian)
17. Zelenokhat N.I. Steady-state stability
of a fl exible interconnection // News
of MPEI, 1996, no. 4, pp. 32–38. (In
Russian)
18. Zelenokhat N.I. Study of operation
specifi cations of an interconnection
with static compensators // Electricity,
1997, no. 3, pp. 13–18. (In Russian)
19. Kirschner L., Retzmann D., Thumm
G. Benefi ts of FACTS for Power Sys-
tem Enhancement. IEEE/PES Trans-
mission and Distribution Conference
and Exhibition: Asia and Pacifi c 2005,
pp. 88-98.
20. Paserba J. How FACTS Controllers
Benefi t AC Transmission Systems
// IEEE PES General Meeting Panel
Session on FACTS Fundamentals.
Denver, Colorado, 2004, pp. 320-
325.
21. Baldick R., Kahn E. Contract paths,
phase shifters, and effi cient elec-
tricity trade. IEEE Transaction on
Power Systems, 1999, vol. 12, no. 2,
pp. 749-755.
22. Sood V.K. HVDC and FACTS Control-
lers. Applications of Static Converters
in Power Systems. Boston: Kluwer
Academic Publishers, 2004, 245 р.
23. 23. Kochkin V.I., Shakaryan Yu.G.
Operating modes of controlled trans-
mission lines // Electricity, 1997, no. 9,
pp. 2–8. (In Russian)
24. Zelenokhat N.I. Improvement of op-
erating mode control effi ciency of
a fl exible interconnection with elec-
trical converters EVPT // News of
MPEI, 2005, no. 3, pp. 66–73. (In
Russian)
25. Zelenokhat N.I. The aspect of energy
exchange between electric associa-
tions of the East and the West and
the principle of combined approach
to its solution // Electro, 2004, no. 2,
pp. 2–5. (In Russian)
26. Venikov V.A., Zelenokhat N.I. and
others. On electromechanical fre-
quency converter application in pow-
er systems // Electricity, 1977, no. 4,
pp. 10–14. (In Russian)
27. Venikov V.A. [at al.] Application of Dig-
ital Computers to the Study of Power
Systems with Asynchronized Electro-
mechanical Frequency Converters.
New-York: Electrical Power &Power
Systems, vol. 1, no. 2, pp. 113-117.
28. Zelenokhat N.I., Makeyechev V.A.,
Vlasova T.A. Dynamic Characteristics
of Electromagnetically Sectionalized
Electrical Station. CIGRE, Sympo-
sium, London, June 1999.
29. Zelenokhat N.I. The aspect of estab-
lishing controllable interconnections
with asynchronous electromechani-
cal frequency converters // News of
MPEI, 1995, no. 4, pp. 97–100. (In
Russian)
30. Zelenokhat N.I. Effi ciency improve-
ment of a fl exible interconnection with
electrical converters EVPT // News
of MPEI, 2005, no. 3, pp. 66–73. (In
Russian)
31. Zelenokhat N.I., Zelenokhat O.N.,
Aristov I.S., Mikryukov D.Yu. Study of
steady-state stability of an intercon-
nection with a power fl ows control-
ler // Power Engineer, 2012, no. 6,
pp. 43–45. (In Russian)
32. Glebov I.A., Sukhanov L.A., Safi ullina
R.Kh. Use of electromechanical fre-
quency converters for power system
connection // News of the Academy of
Sciences of the USSR. Power indus-
try and transport, 1977, no. 6, pp. 49–
57. (In Russian)
33. Zelenokhat N.I. Intelligent UES of
Russia: innovative proposals: prac-
tical guide. Moscow, MPEI Publ.,
2013. 192 p. (In Russian)
34. Kochkin V.I., Shakaryan Yu.G. Ap-
plication of fl exible (controllable) AC
transmission systems in power sys-
tems. Moscow, Torus press Publ.,
2011. 311 p. (In Russian)
35. Shakaryan Yu.G. Asynchronized syn-
chronous machines. Moscow, Ener-
goatomizdat Publ., 1984. 193 p. (In
Russian)
36. Merkur’yev G.V., Shargin Yu.M. Sta-
bility of power systems. Calculations.
Saint-Petersburg, Training center for
power engineers Publ., 2006. 300 p.
(In Russian)
37. Ezhkov V.V., Zelenokhat N.I., Lit-
kens I.V. and others. Transient pro-
cesses in examples and illustrations.
Manual for graduate students. Edited
by Stroyev V.A. Moscow, Znak Publ.,
1996, 224 p. (In Russian)
38. Neuymin V., Ivanov V. and others.
RUSTAB: user manual. TechSystem
Group, 2009. 93 p. (In Russian)
39. Mamikonyants L.G. Study of some
aspects of transient and asynchro-
nous modes of synchronous and
asynchronous machines. Edited by
Shakaryan Yu.G. Moscow, ELEKS-
KM Publ., 2006. 368 p. (In Russian)
40. Peter Van Meirhaeghe. Double fed
induction machine: a EUROSTAG
model // Tractebel Engineering. 2004.
41. Bashkirov O.V., Pershenkov P.P., Ty-
urin E.A. Determination of the con-
sumer contribution into energy quality
indices change // Proc. of Internation-
al symposium “Reliability and Qual-
ity”, 2009 , vol. 2, pp. 77–79. (In Rus-
sian)
42. Dvorkin D.V., Silayev M.A., Tul’skiy
V.N., Palis Sh. Problems of evaluat-
ing the consumer contribution into
energy quality distortion // Electricity,
2017, no. 7, pp. 12–19. (In Russian)
№
2 (65) 2021
Оригинал статьи: Векторное управление режимами электропередачи на основе асинхронизированных синхронных машин
В статье рассмотрена система векторного управления установившимися режимами, переходными процессами и потокораспределением активной мощности в сложнозамкнутой неоднородной электрической сети. Система управления предназначена для контроля асинхронизированного электромеханического преобразователя частоты (АСЭМПЧ), врезанного в линию электропередачи. Получившаяся система предназначена для качественного улучшения условий протекания переходных процессов, вызванных короткими замыканиями, и улучшения параметров установившихся режимов сети. При этом предложенный подход позволяет существенно повысить качество и надежность питания потребителей после ликвидации коротких замыканий. Рассмотрены переходные электромеханические процессы, анализ которых показал, что предложенное векторное управление позволяет существенно сократить качания в энергосистеме и колебания активной мощности после возмущений. В работе отмечено, что применение АСЭМПЧ позволяет на практике реализовать метод баланса искажающих мощностей для определения источников ухудшения качества электрической энергии.