84
Тепловой режим
кабельной линии
в полимерной трубе
УДК
621.315.2.016.2
В
работе
рассмотрен
тепловой
режим
трехфазной
кабельной
линии
,
проложенной
в
тесной
полимерной
трубе
.
Была
созда
-
на
численная
модель
,
учитывающая
кондукционный
,
конвек
-
тивный
и
лучистый
теплообмен
в
данной
линии
.
Указанная
модель
была
верифицирована
путем
сравнения
модельных
результатов
с
результатами
экспериментального
исследо
-
вания
теплового
режима
исследуемой
линии
.
Были
найдены
поправочные
коэффициенты
,
позволяющие
учесть
все
ме
-
ханизмы
теплообмена
в
упрощенной
твердотельной
модели
,
пригодной
для
быстрых
инженерных
расчетов
.
к
а
б
е
л
ь
н
ы
е
л
и
н
и
и
кабельные линии
Лубков
А
.
Н
.,
научный
сотрудник
ОАО
«
НИИПТ
»
Титков
В
.
В
.,
д
.
т
.
н
.,
профессор
,
заведующий
кафедрой
ТВН
Санкт
-
Петербург
-
ского
Политехничес
-
кого
университета
им
.
Петра
Великого
Тукеев
П
.
Д
.,
аспирант
Санкт
-
Петербургского
Политехнического
университета
им
.
Петра
Великого
Ключевые
слова
:
кабельная
линия
,
тепловой
режим
,
полимерная
труба
,
конвекция
,
излучение
,
численная
модель
Keywords:
cable line, thermal
regime, polymer pipe,
convection, radiation,
numerical model
ВВЕДЕНИЕ
Использование
полимерных
труб
для
механической
защиты
кабельной
линии
в
трудных
условиях
про
-
кладки
(
в
частности
,
проколы
всевозможных
пре
-
пятствий
)
становится
причиной
утяжеления
тепло
-
вого
режима
линии
.
Воздух
,
окружающий
фазы
КЛ
,
проложенной
в
трубе
,
является
плохим
проводником
тепла
(
теплопроводность
грунта
и
воздуха
различа
-
ются
в
сотни
раз
).
На
это
обстоятельство
обращено
внимание
в
ряде
работ
[1, 2, 3].
Высокий
нагрев
фаз
кабеля
,
прокладываемых
в
трубах
,
подтверждают
и
факты
частичной
терми
-
ческой
деструкции
труб
,
применяемых
с
этой
целью
[4, 5].
Поскольку
,
с
точки
зрения
теплового
режима
,
применение
полимерных
труб
для
механической
защиты
КЛ
является
самым
меньшим
(
по
сравне
-
нию
со
стальными
),
но
неизбежным
злом
,
то
при
проектировании
КЛ
для
этих
случаев
необходим
дополнительный
анализ
в
части
расчета
рабочей
температуры
кабеля
при
максимальной
проектной
нагрузке
.
Казалось
бы
,
в
современных
условиях
это
не
составляет
серьезной
проблемы
,
благода
-
ря
наличию
всевозможных
расчетных
программ
,
реализующих
метод
конечных
элементов
.
Конеч
-
но
-
элементное
решение
задачи
для
плоского
,
ха
-
рактерного
для
КЛ
,
температурного
поля
доступно
для
большинства
пользователей
соответствующих
программ
.
Многие
конечно
-
элементные
модели
уже
внедрены
в
практику
проектирования
[6]
или
используются
в
учебном
процессе
в
технических
университетах
[7].
Однако
далеко
не
все
так
про
-
сто
с
нашим
случаем
линии
в
трубе
,
поскольку
теплообмен
кабеля
с
грунтом
осуществляется
не
только
твердотельной
теп
ло
про
вод
ностью
,
как
при
непосредственной
укладке
линии
в
грунт
,
но
и
ме
-
ханизмами
конвекции
воздуха
,
присутствующего
в
объеме
трубы
,
а
также
излучением
,
распростра
-
85
няющимся
в
воздушной
области
.
При
этом
матема
-
тическая
модель
усложняется
многократно
.
Далеко
не
все
расчетные
пакеты
позволяют
одновременно
учесть
все
три
указанных
физических
механизма
.
Применение
такой
модели
выводит
задачу
о
нагре
-
ве
кабеля
далеко
за
рамки
инженерных
расчетов
.
Поэтому
результаты
ее
применения
должны
быть
адаптированы
к
практике
проектных
расчетов
.
Это
,
в
свою
очередь
,
возможно
только
после
верифика
-
ции
модели
,
единственным
надежным
инструмен
-
том
которой
является
физический
эксперимент
.
ЗАДАЧИ
РАБОТЫ
1.
Исследование
теплового
режима
кабельной
ли
-
нии
в
полимерной
трубе
методами
физического
эксперимента
и
численно
на
основе
полной
мо
-
дели
теплообмена
,
включающей
кондуктивный
,
конвективный
и
радиационный
теплообмен
.
2.
Верификация
модели
и
разработка
упрощенного
(
инженерного
)
метода
расчета
теплового
режима
КЛ
в
трубе
на
основе
модели
твердотельной
те
-
плопроводности
.
ОПИСАНИЕ
ЭКСПЕРИМЕНТА
Эксперименты
проводились
на
испытательном
стен
-
де
600
кВ
Испытательного
центра
высоковольтного
электрооборудования
(
ИЦ
ВЭ
)
ОАО
«
НИИПТ
».
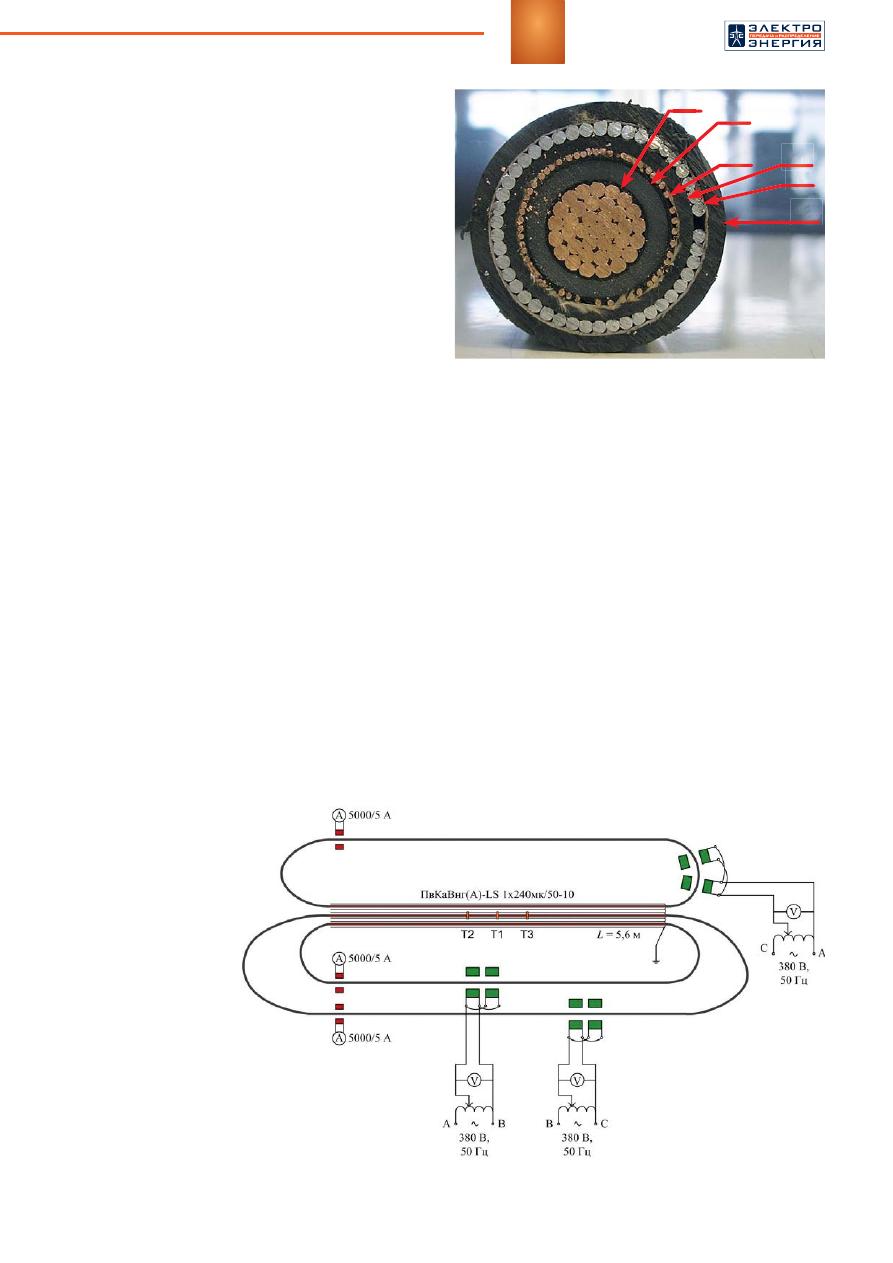
Для
испытаний
были
использованы
три
отрезка
кабеля
марки
ПвКаВнг
(A)-LS 1×240
мк
/50-10
длиной
5,9
м
(
рисунок
1).
На
рисунке
1
обозначено
r
c
= 9,75
мм
—
ради
-
ус
сечения
медной
жилы
,
r
in
1
= 13,75
мм
—
радиус
сечения
внутренней
изоляции
,
r
sh
= 16
мм
—
ради
-
ус
сечения
медного
экрана
,
r
in
2
= 18,5
мм
—
радиус
сечения
внешней
изоляции
,
r
ar
= 20,5
мм
—
ради
-
ус
сечения
брони
и
r
in
3
= 24,5
мм
—
радиус
сечения
внешней
оболочки
.
Образцы
были
размещены
над
полом
с
помощью
изолирующих
подставок
.
Метал
-
лические
(
медные
)
экраны
кабелей
имели
односто
-
роннее
заземление
.
Для
создания
зам
-
кнутой
цепи
нагрева
разделанные
концы
отдельно
каждого
из
испытуемых
образцов
кабелей
соединены
с
помощью
медных
изолированных
прово
-
дов
сечением
300
мм
2
и
длиной
15
м
,
на
кото
-
рых
были
установле
-
ны
трансформаторы
электромагнитного
на
-
грева
.
Нагрев
каждого
кабеля
осуществлял
-
ся
электромагнитным
возбуждением
тока
в
жиле
кабеля
.
Электрическая
схе
-
ма
установки
приве
-
дена
на
рисунке
2.
Измерение
величины
тока
нагрева
каждого
кабе
-
ля
(
каждой
фазы
)
осуществлялось
с
помощью
транс
-
форматоров
тока
,
установленных
на
каждом
кабеле
,
и
амперметров
.
Для
измерения
температуры
нагрева
кабелей
на
кабеле
№
2 (
фаза
B)
в
трех
точках
на
жиле
уста
-
новлены
температурные
датчики
(
термопары
типа
ХК
):
в
центре
отрезка
кабеля
и
на
расстоянии
0,5
м
от
центра
в
сторону
каждого
из
концов
.
Температу
-
ра
воздуха
контролировалась
отдельным
темпера
-
турным
датчиком
.
Измерение
температуры
нагрева
кабелей
и
воздуха
осуществлялось
автоматическим
регистратором
температуры
Термодат
-22
М
2.
Испытания
состояли
из
нагрева
током
по
жилам
каждого
кабеля
(
каждой
фазы
)
до
установившейся
температуры
жилы
90–92°C
в
течение
2
часов
и
вы
-
держку
в
течение
последующих
6
часов
при
указан
-
ной
температуре
.
Температура
нагрева
жил
кабелей
поддерживалась
в
заданных
пределах
путем
регули
-
рования
величины
тока
нагрева
.
При
этом
регулиро
-
вание
тока
нагрева
каждого
кабеля
(
каждой
фазы
)
r
c
r
in
1
r
in
2
r
in
3
r
ar
r
sh
Рис
. 1.
Вид
сечения
кабеля
ПвКаВнг
(
А
)-LS
Рис
. 2.
Электрическая
схема
испытательной
установки
№
3 (48) 2018

86
осуществлялось
независимо
от
других
,
а
ток
под
-
держивался
одинаковым
во
всех
.
При
размещении
кабелей
в
полимерной
трубе
фазы
располагались
в
треугольник
при
двух
ва
-
риантах
вентиляции
трубы
:
–
труба
свободно
продувается
;
–
труба
загерметизирована
на
торцах
(
рису
-
нок
3).
В
данных
опытах
использовалась
широко
применяемая
при
электроэнергетическом
стро
-
ительстве
полимерная
труба
диаметром
160
мм
(
толщина
стенки
трубы
— 10
мм
,
внутренний
диа
-
метр
— 140
мм
).
Длина
трубы
составляла
4,9
м
.
Результаты
измерений
приведены
в
таблице
1.
В
ходе
опыта
с
трубой
с
закрытыми
торцами
также
были
измерены
температуры
на
поверх
-
ности
полимерной
трубы
посередине
ее
дли
-
ны
.
Термопары
были
установлены
в
4-
х
точках
:
сверху
,
снизу
и
по
бокам
.
Результаты
измерений
приведены
в
таблице
2.
Важно
подчеркнуть
,
что
данные
температу
-
ры
в
общем
случае
не
характерны
для
случаев
укладки
в
грунте
:
столь
низкие
значения
обу
-
словлены
укладкой
трубы
на
открытом
воздухе
с
температурой
в
районе
1–2°
С
.
Разница
в
темпе
-
ратурах
в
точках
слева
и
справа
объясняется
не
-
равномерным
режимом
охлаждения
трубы
(
сле
-
ва
имел
место
дополнительный
поток
холодного
воздуха
,
устранить
который
не
представлялось
возможным
).
Представленные
выше
экспериментально
ис
-
следованные
тепловые
режимы
КЛ
близки
к
пре
-
дельным
,
отвечающим
нагрузочной
способности
линии
,
при
которой
температура
ограничена
ве
-
личиной
порядка
90°
С
.
ОПИСАНИЕ
РАСЧЕТНОЙ
МОДЕЛИ
Расчетная
модель
,
в
рамках
которой
можно
про
-
анализировать
результаты
описанного
выше
экс
-
перимента
,
может
быть
построена
на
основе
при
-
ближения
плоских
полей
(
температурного
поля
воздушного
течения
и
радиационного
поля
),
по
-
скольку
отношение
длины
исследуемого
отрезка
КЛ
к
поперечному
сечению
составляет
несколько
десятков
.
Это
дает
основание
для
применения
двухмерных
уравнений
,
описывающих
указанные
про
-
цессы
.
Уравнения
,
описывающие
течение
,
конвективный
и
твердотельный
теплообмен
,
имеют
вид
:
•
уравнение
неразрывности
:
∂
/
∂
t
+ ·(
) = 0,
(1)
где
—
плотность
,
t
—
время
, —
скорость
;
•
уравнение
баланса
импульса
:
∂
(
)/
∂
t
+ ·(
) = –
p
+ ·(
=
) +
g
→
, (2)
где
p
—
статическое
давление
,
=
—
тензор
вязких
на
-
пряжений
,
g
→
—
объемная
плотность
гравитационной
силы
;
•
уравнение
состояния
воздуха
P
=
P
(
,
T
)
задано
таб
-
лично
[8];
•
уравнение
энергии
:
∂
(
E
)/
∂
t
+ ·( (
E
+
p
) = ·(–
T
+
=
·
v
=
+
S
h
, (3)
где
E
—
энергия
на
единицу
массы
вещества
,
T
—
тем
-
пература
;
—
коэффициент
теплопроводности
,
v
=
—
тензор
скорости
деформации
,
S
h
—
объемная
плотность
мощности
—
тепловыделения
от
внешних
источников
(
в
исследуемом
случае
—
джоулевы
потери
);
E
=
h
–
p
/
+
v
2
/2,
где
h
—
энтальпия
.
При
описании
радиационного
теплообмена
в
силу
малых
(
не
более
метров
)
линейных
размеров
воздуш
-
ных
промежутков
,
имеющих
место
в
расчете
,
коэффи
-
циенты
рассеяния
и
поглощения
воздуха
принимаются
равными
0,
а
показатель
рефракции
среды
—
равным
1.
Коэффициент
светимости
черных
поверхностей
кабе
-
лей
и
стенки
трубы
w
был
принят
равным
0,95.
Для
учета
излучения
к
вышеприведенным
уравнени
-
ям
добавляются
выражения
,
описывающие
лучистый
теплообмен
:
·
q
r
= 0,
(4)
На
стенках
выполняются
следующие
граничные
ус
-
ловия
:
J
= (1 –
)
G
+
T
4
, (5)
q
r
=
G
–
J
, (6)
q
r
=
G
–
T
4
, (7)
Рис
. 3.
Вид
кабельной
линии
при
укладке
в
трубе
Табл
. 1.
Результаты
испытаний
нагрева
кабельной
линии
,
уложенной
в
трубе
Торцы
трубы
Установив
-
шийся
ток
,
А
Температура
воздуха
, °C
Температура
жилы
фазы
B, °C
открыты
648 ÷ 650
–0,4 ÷ –0,7
90,9 ÷ 92,0
закрыты
655 ÷ 659
–2,9 ÷ –3,7
89,6 ÷ 93,1
Табл
. 2.
Результаты
измерения
температур
на
внешнем
периметре
сечения
полимерной
трубы
Время
с
начала
нагрева
,
ч
8
Температура
в
точке
слева
, °
С
23,9
Температура
в
точке
справа
, °
С
25,9
Температура
в
верхней
точке
, °
С
30,7
Температура
в
нижней
точке
, °
С
32,1
КАБЕЛЬНЫЕ
ЛИНИИ
87
где
J
—
светимость
точки
;
G
—
освещенность
в
точке
;
q
r
—
входящий
поток
излучения
в
точке
,
Вт
/
м
2
;
—
по
-
стоянная
Стефана
-
Больцмана
,
Вт
/
м
2
·
К
4
;
—
показа
-
тель
светимости
поверхности
;
T
—
температура
,
К
.
Освещенность
каждой
точки
находится
как
совокуп
-
ность
светимостей
точек
,
из
которых
видна
первая
[9].
Тепловыделение
в
жилах
моделировалось
как
объемное
тепловыделение
в
областях
жил
,
величи
-
на
которого
находится
по
формуле
:
q
.
ж
= (
I
ж
2
/
S
ж
2
) ·
м
, (8)
где
I
ж
—
действующее
значение
тока
в
жиле
в
уста
-
новившемся
режиме
,
взятое
из
эксперимента
;
S
ж
—
площадь
сечения
жилы
,
а
м
—
удельное
сопротив
-
ление
жил
,
находимое
по
формуле
:
=
20
·
k
· (1 +
· (T – 20)),
(9)
где
20
= 0,0172
Ом
·
мм
2
/
м
—
удельное
сопро
-
тивление
меди
при
20°
С
;
k
—
поправочный
ко
-
эффициент
резистивности
,
для
исследуемого
кабеля
равный
1,026 [10];
—
температурный
ко
-
эффициент
удельного
сопротивления
меди
,
равный
0,0043 1/
К
[10];
T
—
температура
жилы
.
Для
алюми
-
ния
20
= 0,028
Ом
·
мм
2
/
м
,
а
= 0,0042 1/
К
.
В
силу
незначительных
вследствие
одно
-
стороннего
заземления
экранов
и
малой
длины
испытуемого
участка
величин
вихревых
токов
,
индуцированных
в
кабельных
экранах
в
ходе
экс
-
периментов
,
тепловыделения
в
экранах
в
расче
-
те
не
учитываются
.
К
тому
же
измеренные
в
ходе
эксперимента
токи
в
жилах
для
участка
кабельной
линии
выбранной
длины
оказались
пренебрежимо
малы
вне
зависимости
от
способа
подключения
экранов
.
Теплофизические
свойства
материалов
приведе
-
ны
в
таблицах
3
и
4.
Данные
таблицы
3
взяты
из
[8].
В
[11]
приведены
формулы
,
позволяющие
при
-
ближенно
учесть
влияние
конвекции
и
лучистого
теплообмена
традиционным
способом
,
а
именно
вычислить
значение
поправочного
коэффициента
для
теплопроводности
,
учитывающего
конвективный
и
лучистый
теплообмен
:
T
об
T
тр
(
—
)
4
–
(
—
)
4
100
100
D
D
тр
5,67
·
0,95
·
— ·—·
ln
—
T
об
–
T
тр
2
D
k
попр
=
0,18
(
Gr
·
Pr
)
0,25
+ ——,(10)
где
T
об
—
температура
поверхности
оболочки
кабе
-
ля
,
К
;
T
тр
—
температура
внутренней
поверхности
трубы
,
К
;
D
—
внешний
диаметр
кабеля
,
м
;
D
тр
—
диа
-
метр
внутренней
поверхности
трубы
,
м
;
—
коэффи
-
циент
теплопроводности
воздуха
,
Вт
/
м
·
К
;
Pr
—
чис
-
ло
Прандтля
,
один
из
критериев
подобия
тепловых
процессов
в
жидкостях
и
газах
,
учитывает
влияние
физических
свойств
теплоносителя
на
теплоотдачу
(
для
воздуха
при
температуре
около
0°
С
его
можно
найти
как
Pr
= (
·
C
p
) /
= 0,72,
(11)
где
= 17,2 · 10
-6
Па
·
с
—
динамическая
вяз
-
кость
,
C
p
= 1005
Дж
/
кг
·
К
—
удельная
теплоемкость
,
= 0,024
Вт
/
м
·
К
—
коэффициент
теплопроводности
);
Gr
—
число
Грасгофа
,
критерий
подобия
,
безраз
-
мерная
величина
,
определяющая
процесс
подобия
теплообмена
при
конвекции
в
поле
тяжести
(
грави
-
тации
,
ускорения
)
и
является
мерой
соотношения
архимедовой
выталкивающей
силы
,
вызванной
не
-
равномерным
распределением
плотности
жидкости
,
газа
в
неоднородном
поле
температур
,
и
силами
вяз
-
кости
(
находится
по
формуле
Gr
=
g
·
L
3
·
· (
T
с
–
T
0
) /
2
, (12)
где
g
= 9,81
м
2
/
с
—
ускорение
свободного
падения
;
L
= (
D
тр
–
D
) / 2 —
характерный
размер
поверхности
теплообмена
,
м
;
= 1 / (273,15 +
T
0
) —
температурный
коэффициент
объемного
расширения
теплоносите
-
ля
, 1/
К
;
T
с
—
температура
поверхности
теплообмена
,
в
случае
нагревающегося
кабеля
;
T
0
—
температура
воздуха
в
трубе
;
—
кинематическая
вязкость
воз
-
духа
).
Первое
слагаемое
в
(10)
представляет
собой
по
-
правочный
коэффициент
,
учитывающий
вклад
конвек
-
ции
в
теплообмен
,
второе
—
лучистого
теплообмена
.
В
силу
упрощений
данного
подхода
приведен
-
ные
выше
формулы
более
или
менее
строго
спра
-
ведливы
для
одножильной
КЛ
с
коаксиальным
рас
-
положение
жилы
относительно
трубы
.
Подставив
данные
из
эксперимента
по
укладке
линии
в
трубе
в
приведенные
выше
аналитические
выражения
,
полу
-
чим
значение
поправочного
коэффици
-
ента
для
этого
случая
,
равным
13.
РЕЗУЛЬТАТЫ
ЧИСЛЕННОГО
МОДЕЛИРОВАНИЯ
В
рамках
численных
расчетов
с
ис
-
пользованием
приведенной
выше
пол
-
ной
системы
уравнений
на
внешней
поверхности
полимерной
трубы
было
задано
условие
стационарного
рас
-
пределения
температуры
,
характер
и
величина
которого
взяты
из
экспери
-
ментальных
данных
(
таблица
2)
в
до
-
пущении
линейного
изменения
тем
-
пературы
между
точками
измерения
.
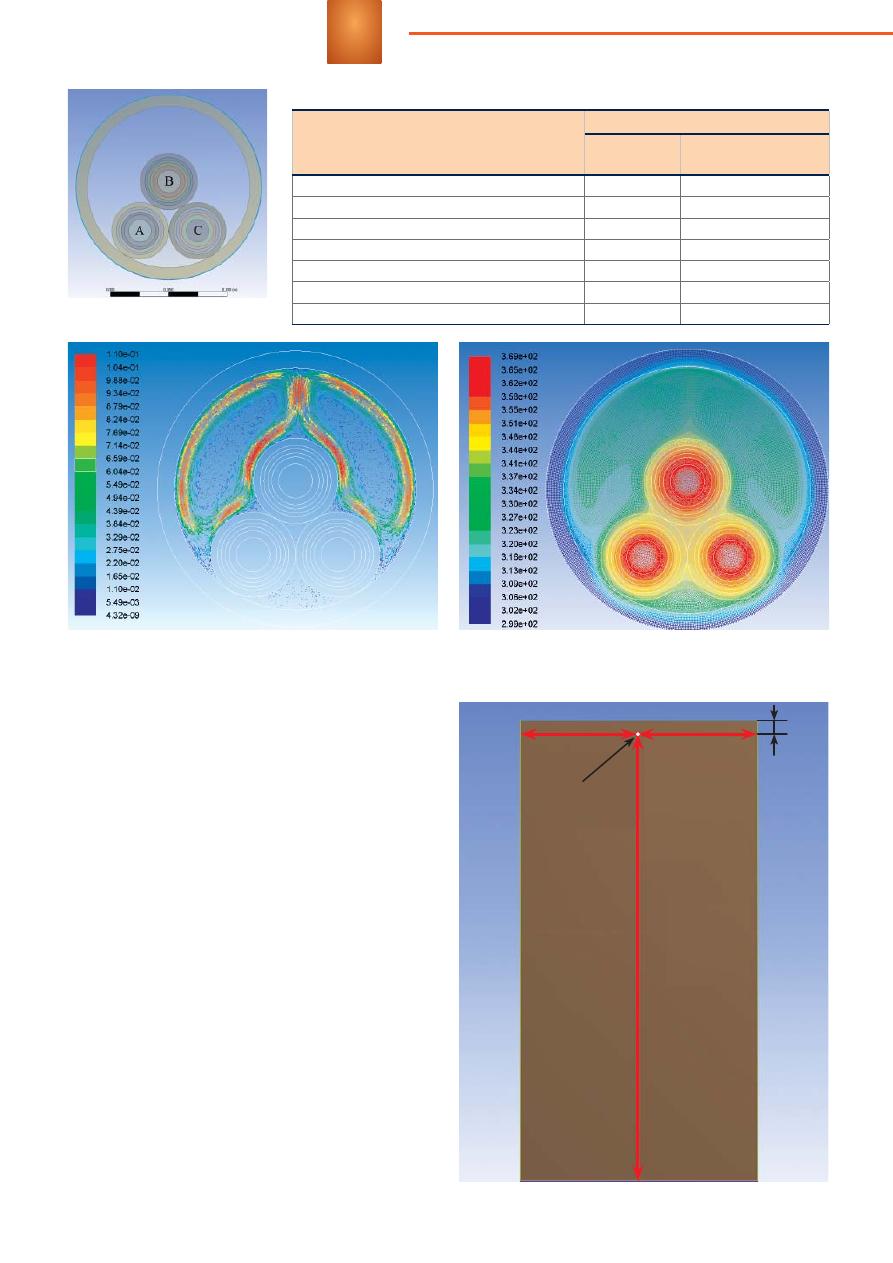
Иллюстрация
расчетной
области
при
-
ведена
на
рисунке
4.
Табл
. 3.
Физические
свойства
воздуха
в
зависимости
от
его
температуры
Температура
, °
С
Свойство
0
100
200
300
500
700
Плотность
,
кг
/
м
3
1,293
0,946
0,747
0,615
0,456
0,362
Теплопроводность
,
Вт
·
м
/
К
0,024
0,032
0,039
0,046
0,057
0,067
Теплоемкость
,
Дж
·
кг
/
К
1003
1007
1024
1045
1093
1135
Динамическая
вязкость
,
Па
·
с
·10
5
1,75
2,23
2,65
3,03
3,62
4,18
Табл
. 4.
Физические
свойства
твердых
материалов
Материал
Свойство
Сшитый
поли
этилен Медь
Алю
-
миний Грунт Бетон
Плотность
,
кг
/
м
3
930
8700
2700
2000
2300
Теплоемкость
,
Дж
·
кг
/
К
2350
385
900
850
880
Теплопроводность
,
Вт
/
м
·
К
0,15
400
238
1
1,7
№
3 (48) 2018
88
На
внешней
поверхности
сечения
полимерной
трубы
задано
стационарное
распределение
темпе
-
ратуры
,
соответствующее
измеренным
значениям
в
4-
х
различных
точках
.
Картина
течений
для
данно
-
го
случая
приведена
на
рисунке
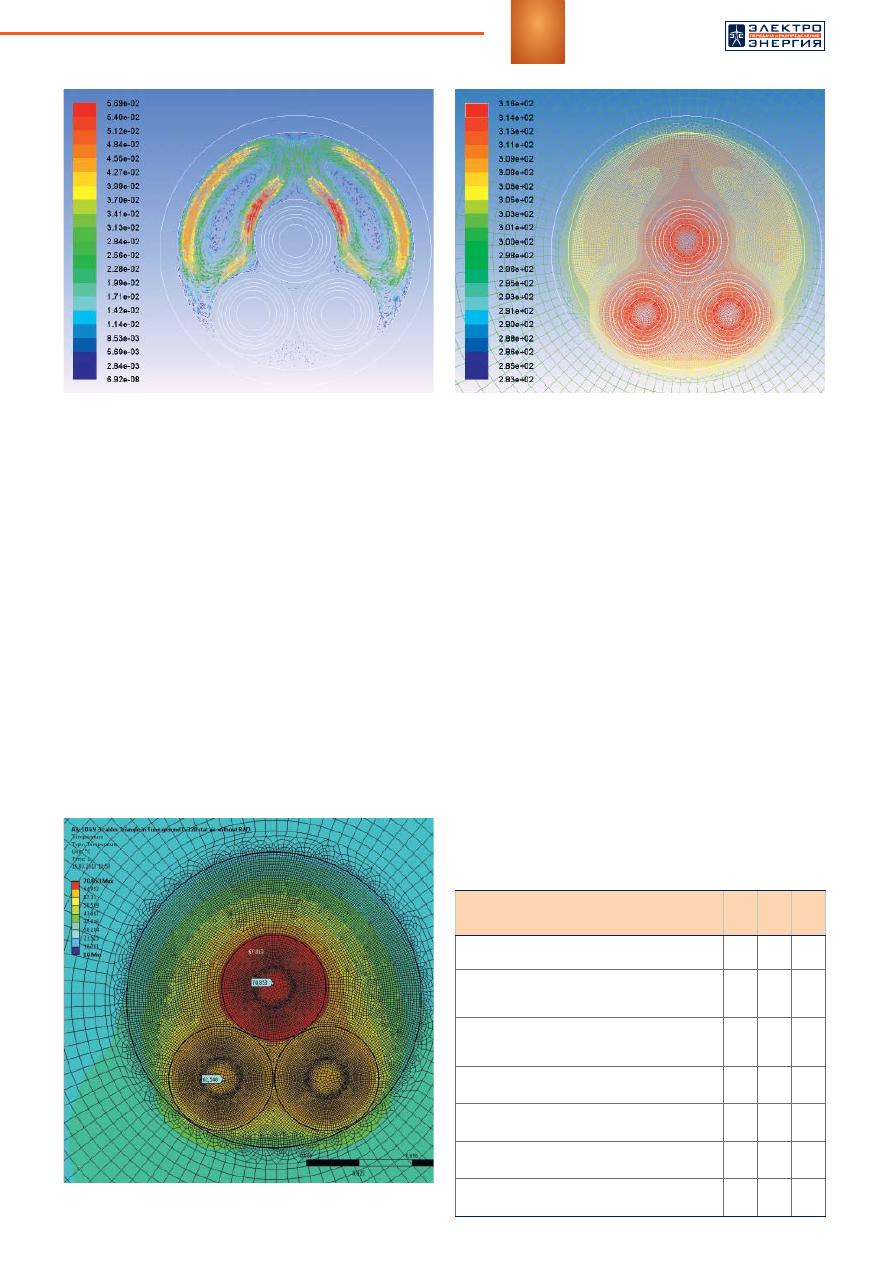
5.
Температурное
поле
для
данного
случая
приведено
на
рисунке
6.
В
таблице
5
сопоставлены
результаты
натурных
и
расчетных
исследований
.
Из
результатов
,
приве
-
денных
в
таблице
,
видно
,
что
предложенная
модель
показывает
приемлемую
для
инженерных
оценок
точность
при
сравнении
с
экспериментом
.
Погреш
-
ность
температуры
жилы
фазы
B
данного
расчета
относительно
экспериментальных
данных
составила
не
более
1%.
Поскольку
применение
описанной
модели
к
анали
-
зу
экспериментальных
данных
дало
удовлетворитель
-
ный
результат
,
то
целесообразно
ее
применение
для
других
случаев
,
относящихся
к
реальной
практике
ис
-
пользования
кабельных
линий
в
электроэнергетике
.
РАСЧЕТ
СЛУЧАЯ
ПРОКЛАДКИ
КАБЕЛЬНОЙ
ЛИНИИ
В
ГРУНТЕ
Далее
проанализируем
тепловые
режимы
кабелей
,
проложенных
в
грунте
с
использованием
полимер
-
ных
труб
.
Рассмотрим
трубу
с
кабелями
,
находящу
-
юся
на
глубине
0,5
м
от
поверхности
грунта
,
ширина
области
грунта
составляет
10
м
,
а
глубина
— 20
м
.
Вид
расчетной
области
и
граничные
условия
при
-
ведены
на
рисунке
7,
где
alpha
= 5
Вт
/
м
2
·
К
—
коэф
-
КАБЕЛЬНЫЕ
ЛИНИИ
Рис
. 4.
Граничные
условия
Рис
. 5.
Картина
течений
для
кабельной
линии
в
трубе
в
предположении
постоянного
во
времени
распределе
-
ния
температуры
внешней
поверхности
трубы
Рис
. 7.
Общий
вид
расчетной
области
и
граничные
усло
-
вия
для
кабельной
линии
в
грунте
Рис
. 6.
Температурное
поле
кабельной
линии
в
трубе
в
предположении
постоянного
во
времени
распределе
-
ния
температуры
внешней
поверхности
трубы
, °
С
Табл
. 5.
Результаты
расчетов
и
экспериментов
и
разница
между
ними
Величина
Способ
укладки
Треугольник
в
трубе
Треугольник
в
трубе
,
упрощенная
модель
Ток
в
фазе
А
,
А
657
657
Ток
в
фазе
B,
А
654
654
Ток
в
фазе
C,
А
653
653
Температура
воздуха
, °
С
–2,9
–2,9
Температура
фазы
B
экспериментальная
, °
С
91,3
91,3
Температура
фазы
B
расчетная
, °
С
85
92
Погрешность
, %
6,5
0,7
Кабельная
линия
в
трубе
Грунт
T
гр
= 10°C
q
= 0
q
= 0
q
=
alpha
· (
T
–
T
окр
)
20
м
5
м
5
м
0,5
м
89
фициент
теплоотдачи
конвективного
теплообмена
из
грунта
в
атмосферу
с
постоянной
температурой
воздуха
T
окр
= 20°
С
;
T
гр
= 10°
С
—
температура
грунта
на
глубине
.
Результаты
расчета
с
моделированием
конвекции
воздуха
в
трубе
для
величины
тока
в
жи
-
лах
I
= 320 A
приведены
на
рисунках
8
и
9.
Картина
теплового
поля
для
данного
случая
приве
-
дена
на
рисунке
9.
Как
видно
из
рисунка
9,
темпера
-
тура
жилы
фазы
B
составляет
41°
С
.
Отчетливо
виден
поднимающийся
и
расширяющийся
поток
воздуха
,
на
-
гретого
кабелями
,
однако
в
силу
замкнутости
простран
-
ства
внутри
полиэтиленовой
трубы
этот
поток
тормо
-
зится
на
внутренней
ее
стенке
,
отдавая
ей
энергию
.
На
рисунке
10
приведено
температурное
поле
линии
в
случае
,
где
воздух
считается
неподвижным
,
а
излучение
не
учитывается
.
Максимальная
температура
жилы
фазы
B
в
дан
-
ном
случае
составила
72°
С
,
что
на
75%
больше
,
чем
при
учете
конвективного
течения
.
Это
свидетель
-
ствует
о
необходимости
учета
конвекции
и
лучистого
теплообмена
в
подобных
расчетах
.
В
рамках
традиционно
применяемых
упрощений
расчета
конвективного
теплообмена
влияние
кон
-
векции
и
излучения
было
учтено
увеличением
коэф
-
фициента
теплопроводности
неподвижного
воздуха
внутри
трубы
.
Величина
коэффициента
подбиралась
таким
образом
,
чтобы
температура
жилы
оказалась
равна
температуре
жилы
,
полученной
в
полноценном
расчете
,
с
погрешностью
не
более
5%.
Помимо
это
-
го
,
была
проведена
серия
расчетов
,
где
поправочный
коэффициент
учитывал
только
влияние
конвекции
,
вклад
лучистого
теплообмена
был
учтен
в
расчете
согласно
уравнениям
,
приведенным
выше
.
Таким
об
-
разом
,
были
получены
поправочные
коэффициенты
,
раздельно
учитывающие
как
конвекцию
,
так
и
излуче
-
ние
.
При
этом
поправочный
коэффициент
теплопро
-
водности
при
использовании
твердотельной
модели
находился
как
сумма
указанных
составляющих
—
из
-
лучательной
k
изл
и
конвективной
k
конв
:
k
=
k
изл
+
k
конв
.
Зависимость
поправочных
коэффициентов
на
конвекцию
и
излучение
от
величины
тока
жилы
при
-
ведены
в
таблице
6.
Рис
. 8.
Картина
течений
воздуха
для
тока
I
= 320 A
Рис
. 9.
Картина
теплового
поля
для
тока
I
= 320 A
Рис
. 10.
Картина
теплового
поля
для
тока
I
= 320 A,
воздух
неподвижен
Табл
. 6.
Зависимость
поправочных
коэффициентов
от
величины
тока
в
жиле
для
трубы
с
D
= 160
мм
Токи
в
жилах
фаз
,
А
320 480 640
Максимальная
температура
линии
с
уче
-
том
конвекции
и
излучения
, °
С
41
73
131
Максимальная
температура
линии
с
не
-
подвижным
воздухом
без
учета
излуче
-
ния
и
конвекции
, °
С
72
160 372
Максимальная
температура
линии
с
не
-
подвижным
воздухом
с
учетом
конвекции
и
излучения
через
коэффициенты
, °
С
42
72
131
Поправочный
коэффициент
на
конвек
-
цию
k
конв
модельный
5
7
7
Поправочный
коэффициент
на
излучение
k
изл
модельный
5
8
8
Поправочный
коэффициент
на
конвек
-
цию
k
конв
,
полученный
по
формуле
3
3
3
Поправочный
коэффициент
на
излучение
k
изл
,
полученный
по
формуле
6
7
9
№
3 (48) 2018

90
ЛИТЕРАТУРА
1.
Дудкин
С
.
М
.,
Титков
В
.
В
.
Кабельные
линии
6–10
кВ
и
выше
.
Влияние
способов
прокладки
на
температур
-
ный
режим
//
Новости
электротех
-
ники
, 2012,
№
3(75).
С
. 38–40.
2. Dudkin S.M., Tadjbaev A.I., Titkov V.V.
Thermalconditionsinthree-phase
cablelinesofmediumandhighVolta
ges, featuring plastic insulation //
Proceedings of the 7-th International
Scienti
fi
c Symposium Electrical Power
Engineering. Elektroenergetika, 2013,
pp. 366–369.
3.
Таджибаев
А
.
И
.,
Титков
В
.
В
.
Влия
-
ние
конвекции
на
тепловой
режим
электроустановок
//
ЭЛЕКТРО
,
2008,
№
6.
С
. 22–26.
4.
Дмитриев
М
.
В
.,
Овсянникова
А
.
Ю
.
О
полиэтиленовых
трубах
для
про
-
кладки
кабельных
линий
//
ЭЛЕК
-
ТРОЭНЕРГИЯ
.
Передача
и
распре
-
деление
, 2015,
№
2(29).
С
. 60–63.
5.
Дмитриев
М
.
В
.
Термическая
стой
-
кость
кабельных
линий
6–500
кВ
.
Требования
к
полиэтиленовым
трубам
//
Кабель
-news, 2014,
№
1.
С
. 28–33.
6.
Грешняков
Г
.
В
.,
Дубицкий
С
.
Д
.,
Ко
-
валев
Г
.
Г
.,
Коровкин
В
.
В
.
Электро
-
магнитный
и
тепловой
расчет
то
-
ковой
нагрузки
кабельной
системы
методом
конечных
элементов
//
Кабели
и
провода
, 2013,
№
4(341).
С
. 15–21.
7.
Бочаров
Ю
.
Н
.
и
др
.
Электроэнер
-
гетика
.
Моделирование
параме
-
тров
и
процессов
высоковольтного
электрооборудования
.
СПб
:
Изд
-
во
Санкт
-
Петербургского
политехниче
-
ского
университета
, 2010. 111
с
.
8.
Справочник
по
теплофизическим
свойствам
газов
и
жидкостей
.
Спра
-
вочник
.
Под
ред
.
Н
.
Б
.
Варгафтика
.
М
.:
Государственное
энергетиче
-
ское
издательство
, 1972. 9
с
.
9.
Эккерт
Э
.
Р
.
Теория
тепло
-
и
массо
-
обмена
.
Пер
.
с
англ
.
под
ред
.
А
.
В
.
Лыкова
М
.-
Л
.:
Госэнергоиздат
, 1961.
С
. 482–490.
10.
Справочник
по
электрическим
уста
-
новкам
высокого
напряжения
.
Под
ред
.
И
.
А
.
Баумштейн
.
М
.:
Энергия
,
1974,
С
. 568.
11.
Кукеков
Г
.
А
.
Выключатели
пере
-
менного
тока
высокого
напряжения
.
2-
е
изд
.,
перераб
.
и
доп
.
Л
.:
Энер
-
гия
, 1972,
С
. 87.
REFERENCES
1. Dudkin S.M., Titkov V.V. Cable
lines with rated voltage 6-10 kV and
above. In
fl
uence of laying methods
on temperature conditions. Electrical
engineering news, 2012, no. 3(75),
pp. 38–40. (in Russian)
2. Dudkin S.M., Tadjbaev A.I., Titkov V.V.
Thermal conditions in three-phase
cable lines of medium and high volt-
ages, featuring plastic insulation.
Proceedings of the 7-th International
Scienti
fi
c Symposium Electrical Pow-
er Engineering. Stara Lesna, Slovak
Republic, 2013, pp. 366–369.
3. Tadjbaev A.I., Titkov V.V. In
fl
uence
of convection on thermal conditions
of electrical installations. ELEKTRO,
2008, no. 6, pp. 22–26. (in Russian)
4. Dmitriev M.V., Ovsyannikova A.Y.
Polyethylene pipes for laying cable
lines. ELECTRIC POWER: Transmis-
sion and Distribution, 2015, no. 2(29),
pp. 60-63. (in Russian)
5. Dmitriev M.V. Thermal resistance of
6-500 kV cable lines. Requirements
for polyethylene pipes. Cabel-news,
2014, no. 1, pp. 28-33. (in Russian)
6. Greshnyakov G.V., Dubitskiy S.D.,
Kovalev G.G., Korovkin V.V. Electro-
magnetic and thermal calculation of
cable system current load by means
of
fi
nite element method. Cables and
wires, 2013, no. 4(341), pp. 15-21. (in
Russian)
7. Bocharov Y.N. et al. Electric power
engineering. Modeling of parameters
and processes of high-voltage electri-
cal equipment. St. Petersburg, SPb-
PU Publ., 2010. 111 p.
8. Handbook of gases and liquids ther-
mophysical properties. Under the
editorship of Vargaftik N.B. Moscow,
Gosudarstvennoye energeticheskoye
izdatelstvo Publ., 1972. 9 p.
9. Ekkert E.R. Theory of heat and mass
transfer. Moscow, Leningrad, Gosen-
ergoizdat Publ., 1961. 681 p.
10. Handbook of high voltage electrical
installations. Under the editorship of
Baumshteyn I.A. Moscow, Energiya
Publ., 1974. 568 p.
11. Kukekov G.A. High voltage AC circuit
breakers. Second edition. Leningrad,
Energiya Publ., 1972. 87 p.
КАБЕЛЬНЫЕ
ЛИНИИ
Из
таблицы
видно
,
что
порядок
величин
попра
-
вочных
коэффициентов
,
находимых
численно
,
мо
-
жет
быть
оценен
с
помощью
аналитических
формул
(15–16).
Также
полученные
результаты
позволяют
судить
о
том
,
что
суммарная
эквивалентная
тепло
-
проводность
воздуха
в
твердотельной
модели
,
учи
-
тывающая
вклад
всех
механизмов
теплообмена
,
со
-
ставляет
не
более
0,7–0,8
Вт
/
м
·
К
,
что
в
2–3
раза
ниже
теплопроводности
грунта
.
Это
позволяет
заключить
,
что
прокладка
трехфазной
кабельной
линии
в
трубе
создает
худший
тепловой
режим
по
сравнению
с
ее
укладкой
непосредственно
в
грунт
.
ЗАКЛЮЧЕНИЕ
Разработана
расчетная
модель
,
учитывающая
весь
набор
физических
явлений
,
происходящих
в
кабель
-
ной
линии
,
проложенной
в
полимерной
трубе
(
нагрев
джоулевым
тепловыделением
,
кондуктивную
,
кон
-
вективную
и
лучистую
теплопередачу
),
обеспечива
-
ет
удовлетворительное
согласие
с
эксперименталь
-
ными
данными
для
тепловых
режимов
,
характерных
для
трехфазных
кабельных
линий
.
Путем
расчетов
,
проведенных
посредством
разработанной
и
протестированной
по
данным
на
-
турного
эксперимента
для
условий
прокладки
трех
фаз
в
общей
трубе
описанной
расчетной
модели
,
найдены
значения
поправочных
коэффициентов
,
учитывающих
влияние
естественной
конвекции
и
излучения
на
тепловой
режим
кабельных
линий
при
исследованном
способе
КЛ
прокладки
в
по
-
лимерных
трубах
.
Поправочные
коэффициенты
существенно
облегчают
оценку
теплового
режима
кабеля
при
массовых
расчетах
с
помощью
широко
применяемой
твердотельной
модели
теплопровод
-
ности
.
Максимальное
значение
эффективного
коэффи
-
циента
теплопроводности
воздуха
с
учетом
конвек
-
тивного
и
лучистого
теплообмена
в
случае
укладки
трехфазной
кабельной
линии
в
одну
трубу
не
превос
-
ходит
0,7–0,8
Вт
/
м
·
К
.
Таким
образом
,
воздух
в
поли
-
мерной
трубе
обеспечивает
худший
тепловой
режим
по
сравнению
с
укладкой
кабеля
непосредственно
в
грунт
.
Поэтому
оценка
нагрузочной
способности
ка
-
бельных
линий
в
трубах
должна
учитывать
данное
обстоятельство
.
В
дальнейшем
целесообразно
применить
разра
-
ботанную
и
верифицированную
в
рамках
в
данной
работы
расчетную
модель
для
оценок
теплового
ре
-
жима
КЛ
при
пофазной
укладке
кабелей
в
полимер
-
ных
трубах
.
Оригинал статьи: Тепловой режим кабельной линии в полимерной трубе
В работе рассмотрен тепловой режим трехфазной кабельной линии, проложенной в тесной полимерной трубе. Была создана численная модель, учитывающая кондукционный, конвективный и лучистый теплообмен в данной линии. Указанная модель была верифицирована путем сравнения модельных результатов с результатами экспериментального исследования теплового режима исследуемой линии. Были найдены поправочные коэффициенты, позволяющие учесть все механизмы теплообмена в упрощенной твердотельной модели, пригодной для быстрых инженерных расчетов.