Оригинал статьи: Тепломассообмен в кабельных туннелях
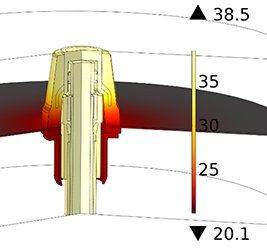
Кабельный туннель — это подземное сооружение с расположенными в нём опорными конструкциями для размещения на них кабельных линий, позволяющее производить прокладку, ремонты и осмотры со свободным проходом по всей длине.