Статическая устойчивость в задачах надежности магистральных электрических сетей энергосистем

46

Статическая устойчивость 
в задачах надежности 
магистральных электрических 
сетей энергосистем

УДК

 621.3.051.2

Непомнящий

 

В

.

А

., 

д

.

э

.

н

., 

профессор

, 

академик

 

РАЕН

Ключевые

 

слова

:

статическая

 

устой

 

чи

 

вость

, 

сечение

, 

якобиан

, 

угол

 

передачи

 

мощности

Keywords:

steady-state stability, critical section, 
Jacobian, power angle

В

 

статье

 

обосновывается

 

возможность

 

применения

 

в

 

задачах

 

надежности

 

оценки

 

статической

 

устойчивости

 

энергосистем

 

при

 

аварийных

 

отключениях

 

магистральных

 

ЛЭП

 

критерия

 

перехода

 

через

 

ноль

 

якобиана

 

системы

 

урав

-

нений

 

послеаварийного

 

режима

, 

а

 

вместо

 

выявления

 

и

 

контроля

 «

опасных

 

сечений

» 

предлагается

 

вычислять

 

и

 

контролировать

 

поток

 

мощности

 

по

 

ЛЭП

 

с

 

наибольшим

 

углом

 

передачи

.

П

о

 

настоящее

 

время

 

расчеты

 

статической

 

устойчивости

 

энергосистем

 

проводятся

 

в

 

соответствии

 

с

 

рекомендациями

 [1], 

со

-

гласно

 

которым

 

в

 

электрической

 

сети

 

выде

-

ляются

 

определенные

 

совокупности

 

электрических

 

связей

, 

включающих

 

в

 

себя

 

одну

 

или

 

несколько

 

ЛЭП

, 

возможно

, 

разного

 

класса

 

напряжения

, 

отключение

 

которых

 

разделяет

 

энергосистему

 

на

 

изолировано

 

работающие

 

части

. 

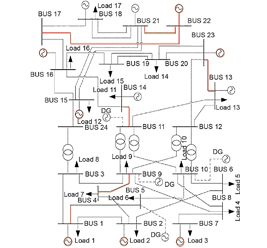
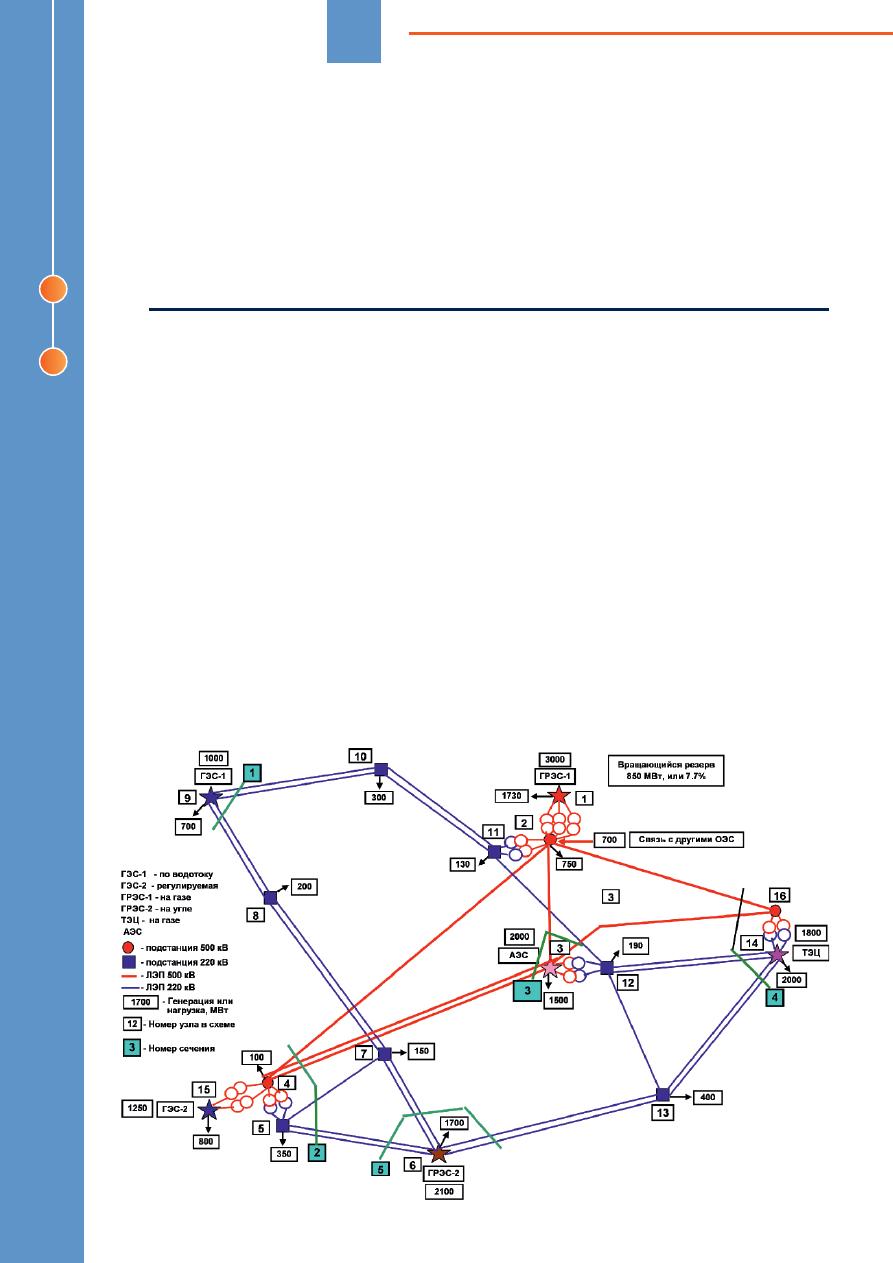
Пример

 

схемы

 

магистральных

 

сетей

 500–220 

кВ

 

с

 

выделенными

 

возможными

 

сече

-

ниями

 

представлен

 

на

 

рисунке

 1.

Рис

. 1. 

Схема

 

магистральных

 

сетей

 

500–220 

кВ

 

с

 

выделением

 

возможных

 

сечений

 

(

генерация

 

и

 

нагрузки

 

зимнего

 

максимума

)

УПРАВЛЕНИЕ

СЕТЯМИ

у

п

р

а

в

л

е

н

и

е

 с

е

т

я

м

и

управление сетями

47

Из

 

приведенной

 

схемы

 

видно

, 

что

 

задача

 

фор

-

мирования

 

расчетных

 

сечений

 

для

 

оценки

 

статиче

-

ской

 

устойчивости

 

не

 

имеет

 

однозначного

 

решения

, 

а

 

значит

, 

и

 

однозначного

 

результата

. 

При

 

этом

 

может

 

оказаться

, 

что

 

при

 

различных

 

составах

 

сечений

 

одни

 

и

 

те

 

же

 

возмущения

  (

отключения

 

ЛЭП

 

или

 

погаше

-

ния

 

узлов

 

схемы

) 

могут

 

вызывать

 

или

 

не

 

вызывать

 

нарушении

 

статической

 

устойчивости

 

энергосисте

-

мы

. 

Если

 

при

 

этом

 

расчеты

 

проводятся

 

методом

 

«

утяжеления

» 

режима

, 

то

 

на

 

зону

 

неопределенности

 

существенное

 

влияние

 

будет

 

оказывать

 

выбранная

 

траектория

 

утяжеления

.

Поэтому

 

для

 

повышения

 

стабильности

 

резуль

-

татов

 

расчетов

 

статической

 

устойчивости

 

следует

 

использовать

 

другие

 

принципы

 

ее

 

определения

, 

не

 

менее

 

корректные

 

в

 

теоретическом

 

отношении

, 

чем

 

метод

 «

сечений

 

и

 

утяжеления

», 

но

 

обладающие

 

од

-

нозначностью

 

получаемых

 

решений

. 

Одним

 

из

 

таких

 

принципов

 

является

 

сочетание

 

расчета

 

установившегося

 

электрического

 

режима

 

методом

 

декомпозиции

 

P

 

→

 



, 

Q

 

→

 

U

, 

разработан

-

ного

 B. Stott [2] 

и

 

развитого

 

далее

 

Т

.

Х

. 

Насыровым

 

[3, §8.6], 

с

 

методом

 

оценки

 

статической

 

устойчивости

 

энергосистемы

 

по

 

критерию

 

перемены

 

знака

 

якоби

-

ана

 

системы

 

уравнений

 

установившегося

 

режима

 

при

 

использовании

 

упрощенной

 

матрицы

 

Якоби

 [2] 

в

 

форме

 

∂



' 

∂



' 

∂



'

 

—  — 

—

  0

 

∂



 

∂

U

 

∂



 

                 

≈

                 , (1)

 

∂



" 

∂



"  

∂



"

 

—  —

 

0

  —

 

∂



 

∂

U

 

 

∂

U

где

 



'

 

и

 



" 

— 

соответственно

 

вещественная

 

и

 

мни

-

мая

 

составляющие

 

уравнения

 

установившегося

 

ре

-

жима

, 

записанные

 

в

 

форме

 

балансов

 

активных

 

и

 

ре

-

активных

 

мощностей

 

P

 

и

 

Q

.

Такое

 

упрощение

 

матрицы

 

Якоби

 

сводит

 

опреде

-

ление

 

параметров

 

установившегося

 

режима

 

к

 

реше

-

нию

 

двух

 

независимых

 

подсистем

 

∂



'

 

 —   

× 



 = – 



' 

 

∂



 

∂



"

 

 —   

× 



U

 = – 



"

 

(2)

 

∂

U

Принимая

 

во

 

внимание

, 

что

 

в

 

сетях

 220 

кВ

 

и

 

выше

 

активное

 

сопротивление

 

существенно

 

меньше

 

реак

-

тивного

, 

и

 

используя

 

рекомендации

 [2, 3], 

можно

 

пре

-

небречь

 

активной

 

проводимостью

 

сети

 

и

 

использо

-

вать

 

в

 

расчетах

 

симметричную

 

матрицу

 

реактивных

 

узловых

 

проводимостей

 [

Y

].

 

Y

 = 

Y

 

e

–

j

90°

 = –

jY

. (3)

Целесообразно

 

также

 

зарядные

 

мощности

 

ЛЭП

 

и

 

мощности

 

шунтирующих

 

реакторов

  (

ШР

), 

вычис

-

ленные

 

при

 

номинальных

 

напряжениях

, 

включить

 

в

 

состав

 

реактивных

 

нагрузок

 

узлов

.

Как

 

утверждается

 

в

 [2], 

предлагаемые

 

упрощения

 

уже

 

на

 1-

й

 

итерации

 

обеспечивают

 

погрешность

 

по

 



 

и

 

U

 

около

 0,2 % 

в

 

нормальных

 

режимах

 

и

 

до

 2 % 

в

 

послеаварийных

 

режимах

, 

что

 

можно

 

считать

 

впол

-

не

 

приемлемым

, 

учитывая

 

погрешность

 

в

 

оценках

 

нагрузок

 

в

 

узлах

 

не

 

менее

 5 %.

С

 

учетом

 

этих

 

упрощений

 

вещественная

 

и

 

мни

-

мая

 

составляющие

 

уравнений

 

установившегося

 

ре

-

жима

 

в

 

форме

 

балансов

 

мощностей

 

запишутся

 

как

 

функции

 

модулей

 

напряжения

 

U

 

и

 

фазовых

 

углов

 



:

 

n

y

 



'

(

U, 



 

U

i

U

k

Y

ik

sin

(



i

 – 



k

) – 

P

i

нагр

 + 

P

i

ген

 = 0,

 

 

k 

≠

 

i

 

n

y



"

(

U, 



Y

ii

U

i

2

 – 

U

i

U

k

Y

ik

cos

(



i

 – 



k

) – 

Q

i

нагр

 + 

Q

i

ген

 = 0.



(5)

 

k 

≠

 

i

где

 

Y

ii

 

и

 

Y

ik

 — 

элементы

 

матрицы

 

реактивных

 

узловых

 

проводимостей

; 

n

y

 — 

количество

 

узлов

 

в

 

расчетной

 

схеме

 

сети

; 

P

i

нагр

 

и

 

Q

i

нагр

 — 

активная

 

и

 

реактивная

 

на

-

грузка

 

потребителей

 

в

 

узлах

; 

P

i

ген

 

и

 

Q

i

ген

 — 

активная

 

и

 

реактивная

 

генерирующие

 

мощности

 

в

 

узлах

.

Результирующие

 

значения

 

нагрузки

/

генерации

 

в

 

i

–

м

 

узле

 

будут

 

равны

 

P

i

 = 

P

i

нагр

 – 

P

i

ген

, (6)

 

Q

i

 = 

Q

i

нагр

 – 

Q

i

ген

 + 

Q

ШР

i

 – 

Q

ЛЭП

i

, (7)

где

 

Q

ШР

i

 

и

 

Q

ЛЭП

i

 — 

мощность

 

шунтирующих

 

реакторов

 

и

 

зарядная

 

мощность

 

ЛЭП

 

в

 

i

-

м

 

узле

.

Формулы

 

расчета

 

установившегося

 

режима

 

элек

-

трической

 

сети

 

приведены

 

ниже

. 

Алгоритм

 

расчета

 

включает

 

в

 

себя

 

две

 

полуите

-

рации

.

1-

я

 

полуитерация

а

) 

определение

 

токов

 

в

 

узлах

:

 

n

y

 

I

i

'



Y

ii

U

i

"   –



 

Y

ik

U

k

"



 

k 

≠

 

i

 

n

y

 

I

i

"



–

Y

ii

 +



 

Y

ik

U

k

'       

;



(8)

 

k 

≠

 

i

б

) 

определение

 

небалансов

 

активной

 

мощности

 

в

 

узлах

:

 



P

i

 = 

U

i

'   I

i

'

 + 

U

i

"   I

i

"

 – 

P

i

; (9)

в

) 

определение

 

поправки

 

к

 

фазовым

 

углам

:





P

 

[



] = [

X

] × 

 – — 

, 

где

 [

X

] = [

Y

]

–1

; (10)



U

2

г

) 

минимизация

 

вектора

 

поправок

 

к

 

фазовым

 

углам

:

 

F

(

P

ген

) = 

 



i

2 

(

P

ген

) 

→

 

min

; (11)

д

) 

корректировка

 

напряжений

 

в

 

узлах

 

по

 

фазовому

 

углу

:

 

U'

(

t

+1)

i

 = 

U'

(

t

)

i

cos

(



i

) – 

U"

(

t

)

i

 

sin

(



i

) 

 

U"

(

t

+1)

i

 = 

U"

(

t

)

i

cos

(



i

) + 

U'

(

t

)

i

 

sin

(



i

)

; (12)

2-

я

 

полуитерация

а

) 

определение

 

токов

 

в

 

узлах

:

 

n

y

 

I

i

'



Y

ii

U

i

"   –



 

Y

ik

U

k

"



 

k 

≠

 

i

 

n

y

 

I

i

"



–

Y

ii

 +



 

Y

ik

U

k

'       

;



(13)

 

k 

≠

 

i

б

) 

определение

 

небалансов

 

реактивной

 

мощности

 

в

 

узлах

:

 



Q

i

 = 

U

i

"   I

i

'

 + 

U

i

'   I

i

"

 – 

Q

i

; (14)

в

) 

определение

 

вектора

 

поправок

 

к

 

модулям

 

напря

-

жений





Q

 

[



U

] = [

X

] × 

 – — 

; (15)



U

2

Входящие

 

в

 (9) 

и

 (14) 

P

i

 

и

 

Q

i

 

вычисляются

 

по

 

вы

-

ражениям

 (6) 

и

 (7).

№

 3 (42) 2017

48

г

) 

корректировка

 

напряжений

 

по

 

модулю

:

 

U'

(

t

+1)

i

 = 

U'

(

t

)

i

(1 + 



U

i 

/

U

i

) 

 

U"

(

t

+1)

i

 = 

U"

(

t

)

(1 + 



U

i 

/

U

i

)

; (16)

д

) 

ввод

 

режима

 

в

 

допустимую

 

по

 

напряжению

 

об

-

ласть

:

 

n

y



U

i

(

Q

ген

) 

2 

U

i

min 

2

F

(

Q

ген

) =  ( 

 —

 – 1

   

+ 

 —

 – 1

   

) 

→

 

min

. (17)

 

k 

≠

 

i



U

i

min

 

>0

 

U

i

(

Q

ген

)

 

>0

Минимизация

 

приращений

 

фазовых

 

углов

 (10) 

осуществляется

 

за

 

счет

 

изменения

 

генерации

 

актив

-

ной

 

мощности

 

в

 

узлах

, 

а

 

ввод

 

режима

 

в

 

допустимую

 

по

 

напряжению

 

область

 (17) 

проводится

 

путем

 

изме

-

нения

 

генерации

 

в

 

узлах

 

реактивной

 

мощности

 

гене

-

раторов

 

и

 

синхронных

 

компенсаторов

.

В

 

обоих

 

случаях

 

наиболее

 

эффективным

 

в

 

вы

-

числительном

 

аспекте

 

является

 

метод

 

проекции

 

градиента

 [5], 

усовершенствованный

 

автором

 

при

-

менительно

 

к

 

решениям

 

рассматриваемых

 

задач

 

и

 

изложенный

 

в

 [7].

Для

 

оценки

 

статической

  (

апериодической

) 

устойчивости

 

послеаварийного

 

установившегося

 

режима

  (

ПАР

) 

воспользуемся

 

корректным

 

и

 

эф

-

фективным

 

критерием

 

перемены

 

знака

 

якобиана

 

системы

 

линеаризированных

 

уравнения

 

устано

-

вившегося

 

режима

, 

составленной

 

с

 

учетом

 

всех

 

функциональных

 

связей

 

между

 

нагрузкой

, 

часто

-

той

 

и

 

напряжением

. 

Согласно

 [6] 

этот

 

якобиан

 

совпадает

 

со

 

свободным

 

членом

 

характеристи

-

ческого

 

уравнения

 

системы

 

линеаризированных

 

дифференциальных

 

уравнений

 

маловозмущен

-

ного

 

движения

 

системы

. 

При

 

от

c

утствии

 

саморас

-

качивания

 

критерием

 

статической

 

устойчивости

 

энергосистемы

 

является

 

равенство

 

этого

 

якобиа

-

на

 

нулю

.

Для

 

упрощения

 

расчетов

 

по

 

выявлению

 

области

 

статической

 

устойчивости

 

режима

 

системы

 

в

 [6] 

ре

-

комендуется

 

сопоставлять

 

знак

 

якобиана

 

исследуе

-

мого

 

режима

 

со

 

знаком

 

якобиана

 

заведомо

 

устойчи

-

вого

 

режима

 

при

 

его

 

последовательном

 

утяжелении

. 

Первая

 

же

 

перемена

 

знака

 

якобиана

 

будет

 

свиде

-

тельствовать

 

о

 

нарушении

 

статической

 (

апериодиче

-

ской

) 

устойчивости

.

Для

 

оценки

 

апериодической

 

статической

 

устой

-

чивости

 

режима

 

энергосистемы

 

предположим

,

что

:

1) 

все

 

электростанции

 

в

 

расчетной

 

схеме

 

энерго

-

системы

 

снабжены

 

устройствами

 

АРВ

 

сильного

 

действия

, 

обеспечивающими

 

в

 

избыточных

 

по

 

ге

-

нерации

 

узлах

 

постоянство

 

напряжения

 

на

 

шинах

 

ВН

 

электростанций

;

2) 

все

 

возникающие

 

в

 

энергосистеме

 

аварийные

 

не

-

балансы

 

мощности

 

ликвидируются

 

системой

 

про

-

тивоаварийной

 

автоматики

  (

ПАА

) 

и

 

поэтому

 

все

 

послеаварийные

 

режимы

 

устанавливаются

 

при

 

номинальной

 

частоте

.

Якобиан

 

системы

 

уравнений

 

установившегося

 

ре

-

жима

 

в

 

общем

 

виде

 

имеет

 

вид

:

 

∂



' 

∂



'

 

—  —

 

∂



 

∂

U

 

D

(n

y

)

 

=

 

det

                   

, (18)

 

∂



" 

∂



"

 

—  —

 

∂



 

∂

U

где

 

элементы

 

матрицы

 

Якоби

 

представляют

 

собой

 

производные

 

функций

 (4) 

и

 (5) 

по

 

фазовым

 

углам

 

и

 

модулям

 

напряжений

 



 

и

 

U

. 

При

 

этом

 

для

 

баланси

-

рующего

 (

опорного

) 

узла

 



0

 = 0 

и

 

U

0

 = 

const

.

Входящие

 

в

 

матрицу

 (18) 

элементы

 

имеют

 

вид

 

∂



'

 

n

y

 

— 

= 

U

i

   

U

k 

Y

ik

 

cos

(



i

 – 



k

)

 

∂



i

 

k 

≠

 

i

 

∂



'

 

n

y

 

— 

=   

U

k 

Y

ik

 

sin

(



i

 – 



k

)

 

∂

U

i

 

k 

≠

 

i

 

∂



'

 

— 

= 

U

i

 

U

k 

Y

ik

 

cos

(



i

 – 



k

)

 

∂



k

 

∂



'

 

— 

= 

U

i 

Y

ik

 

sin

(



i

 – 



k

)

 

∂

U

k

 

                                                  

(19)

 

∂



"

 

n

y

 

— 

= 

U

i

   

U

k 

Y

ik

 

sin

(



i

 – 



k

)

 

∂



i

 

k 

≠

 

i

 

∂



"

 

n

y

 

— 

= 2

Y

ik

 –   

U

k 

Y

ik

 

cos

(



i

 – 



k

)

 

∂

U

i

 

k 

≠

 

i

 

∂



"

 

— 

= – 

U

i

 

U

k 

Y

ik

 

sin

(



i

 – 



k

)

 

∂



k

 

∂



"

 

— 

= – 

U

i 

Y

ik

 

cos

(



i

 – 



k

)

 

∂

U

k

Критерием

 

достижения

 

предела

 

статической

 

устойчивости

 

является

 

равенство

 

нулю

 

якобиана

 

D

(n

y

)

 (18). 

Однако

 

в

 

задачах

 

надежности

 

нас

 

интере

-

сует

 

не

 

столько

 

сам

 

предел

 

статической

 

устойчиво

-

сти

 

системы

, 

сколько

 

выявление

 

факта

 

устойчивости

 

или

 

неустойчивости

 

исследуемого

 

послеаварийного

 

(

ремонтного

) 

режима

 

при

 

заданных

 

значениях

 

нагру

-

зок

 

в

 

узлах

.

Для

 

этого

 

согласно

 [6] 

необходимо

 

сопоставить

 

знак

 

якобиана

 

исследуемого

 

режима

 

со

 

знаком

 

яко

-

биана

 

заведомо

 

устойчивого

 

режима

 

при

 

той

 

же

 

структуре

 

электрической

 

сети

. 

Различие

 

в

 

знаках

 

этих

 

якобианов

 

будет

 

свидетельствовать

 

о

 

неустой

-

чивости

 

исследуемого

 

режима

.

Анализ

 

выражения

 (18) 

с

 

учетом

 

зависимостей

 

(19) 

показал

, 

что

 

якобиан

 

заведомо

 

устойчивого

 

режима

, 

близкого

 

к

 

режиму

 

холостого

 

хода

 

энерго

-

системы

  (

при

 

отсутствии

 

самораскачивания

), 

когда

 

P 

→

 0 

и

 



→

 0 

можно

 

вычислить

 

по

 

формуле

:

 

n

y

 

n

y

D

(n

y

)

уст

 



U

k  

× 

det

[

Y

]

n

y

 

× 

det

[

Y

]

n

y

 



U

k 

 

× (

det

[

Y

]

n

y

)

2

 > 0



(20)

 

k 

≠

 

i

 

k 

≠

 

i

где

 [

Y

]

n

y

 — 

матрица

 

узловых

 

проводимостей

 

размер

-

ностью

 

n

y

 × 

n

y

.

Таким

 

образом

, 

якобиан

 

заведомо

 

устойчивого

 

режима

, 

близкого

 

к

 

режиму

 

холостого

 

хода

, 

всегда

 

положительный

. 

Поэтому

 

отрицательность

 

якобиа

-

на

 

послеаварийного

 

установившегося

 

режима

 

будет

 

свидетельствовать

 

о

 

нарушении

 

статической

 (

апери

-

одической

) 

устойчивости

 

энергосистемы

.

Нарушение

 

статической

 

устойчивости

 

энергосис

-

темы

 

может

 

быть

 

вызвано

 

глубокими

 

понижениями

 

напряжения

 

в

 

узлах

 

сети

 

в

 

послеаварийных

 

режи

-

мах

. 

При

 

этом

 

углы

 

векторов

 

напряжений

 

могут

 

не

 

достигать

 

предельных

 

значений

, 

а

 

якобиан

 — 

ну

-

левого

 

значения

. 

В

 [1] 

минимальный

 

коэффици

-

ент

 

запаса

 

устойчивости

 

по

 

напряжению

 

принят

 

в

 

размере

 10–15 %, 

однако

 

статистический

 

анализ

 

УПРАВЛЕНИЕ

СЕТЯМИ

49

большого

 

количества

 

расчетов

 

статической

 

устой

-

чивости

 

энергосистем

 

показал

, 

что

 

минимальный

 

уровень

 

напряжения

, 

приводящий

 

к

 

нарушению

 

устойчивости

, 

с

 

учетом

 

возможностей

 «

встречного

 

регулирования

» 

составляет

 75–80 % 

от

 

номиналь

-

ного

 

значения

. 

В

 

задачах

 

надежности

 

магистральных

 

электриче

-

ских

 

сетей

 

исключительно

 

важным

 

этапом

 

является

 

ввод

 

режима

 

в

 

допустимую

 

по

 

устойчивости

 

и

 

напря

-

жению

 

область

 

для

 

снижения

 

вероятных

 

ущербов

 

от

 

нарушений

 

электроснабжения

.

Математически

 

эту

 

задачу

 

можно

 

сформулиро

-

вать

 

следующим

 

образом

.

Необходимо

 

минимизировать

 

функцию

: 

 

F

(

P

нагр

,

P

ген

) = –

D

(n

y

)

(

P

нагр

,

P

ген

) 

→

 0 

(21)

при

 

ограничениях

:

 

n

y

 

n

y

 

h

1

 ( 

.

P

U

) 



 

P

Н

i

 – 

 

P

Г

i

 = 0

,

 (22)

 

i

=0

 

i

=0

 

g

1

( 

.

P

Г

) 



P

Г

i

 

≥

 0 

при

 

i

 = 0, …, 

n

у

,

  

(23)

 

g

2

( 

.

P

Г

) 



P

Г

i

 

≤

 

P

Г

i

расп

 

при

 

i

 = 0, …, 

n

у

,

  

(24)

 

g

3

(  

.

U

 

) 



U

i

min

 

≤

 

U

i

 

≤

 

U

i

min

 

для

 

i

 = 1, …, 

n

у

. (25)

Режим

 

будет

 

считаться

 

введенным

 

в

 

допустимую

 

область

, 

если

 

выражение

 (21) 

будет

 

равно

 

нулю

.

Для

 

решения

 

этой

 

задачи

 

воспользуемся

 

упомя

-

нутым

 

выше

 

модернизированным

 

методом

 

проекции

 

градиента

.

Ввод

 

режима

 

в

 

допустимую

 

область

 

осуществля

-

ется

 

в

 

два

 

этапа

:

 

–

на

 1-

м

 

этапе

 

проводится

 

перераспределение

 

нагрузок

 

между

 

генерирующими

 

источниками

 

с

 

учетом

 

соблюдения

 

условий

 (24) 

и

 (25);

 

–

если

 

при

 

этом

 

выражение

 (21) 

не

 

достигает

 

равенства

 

нулю

, 

то

 

переходим

 

ко

 2-

му

 

этапу

 

регу

-

лирования

 

режима

 — 

выборочному

 

ограничению

 

нагрузок

 

потребителей

 

в

 

узлах

.

При

 

вводе

 

режима

 

в

 

допустимую

 

по

 

статической

 

устойчивости

 

область

 

важной

 

задачей

 

является

 

обес

 

печение

 

нормативного

 

запаса

 

устойчивости

, 

характеризуемого

 

значением

 

коэффициента

 

k

з

ст

.

у

, 

который

 

регламентируется

 

в

 [1] 

в

 

размере

 20 % 

для

 

нормальных

 

и

 8 % 

для

 

послеаварийных

 (

вынужден

-

ных

) 

режимов

.

При

 

определении

 

предела

 

статической

 

устойчи

-

вости

 

предлагаемым

 

в

 [1] 

традиционным

 

методом

 

утяжеления

 

потока

 

мощности

 

в

 

определенных

 

сече

-

ниях

 

задача

 

решается

 

снижением

 

предельного

 

пото

-

ка

 

на

 

величину

 

k

з

ст

.

у

.

При

 

оценке

 

же

 

предела

 

статической

 

устойчивости

 

энергосистемы

 

по

 

критерию

 

равенства

 

нулю

 

якобиа

-

на

 (21) 

без

 

явного

 

выделения

 

контролируемых

 

сече

-

ний

 

задача

 

несколько

 

усложняется

.

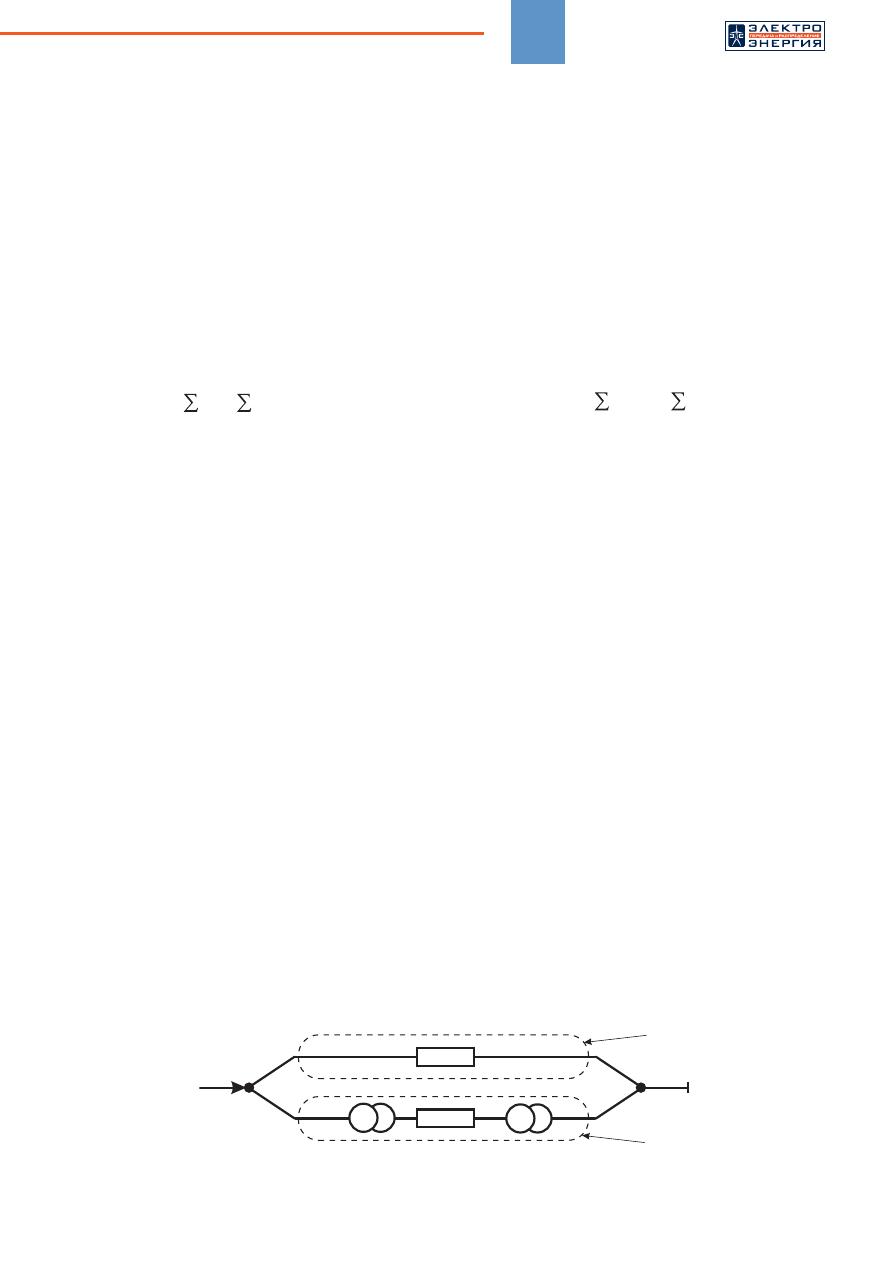
Для

 

ее

 

решения

 

рассмотрим

 

некоторое

 

сечение

, 

включающее

 

в

 

себя

 

ЛЭП

 

разных

 

классов

 

напряже

-

ния

 (

рисунок

 2).

Таким

 

образом

, 

в

 

общем

 

случае

 

любое

 

сечение

 

электрической

 

сети

 

представляет

 

собой

 

неоднород

-

ный

 

контур

 

ЛЭП

 

разного

 

класса

 

напряжения

.

Как

 

известно

 

из

 

теории

 

электрических

 

сетей

, 

распределение

 

потоков

 

активной

 

мощности

 

по

 

ветвям

 

неоднородного

 

контура

 

происходит

 

про

-

порционально

 

реактивным

 

проводимостям

 

этих

 

ветвей

  [

Y

р

], 

а

 

распределение

 

реактивной

 

мощ

-

ности

 — 

пропорционально

 

активным

 

проводимо

-

стям

, 

то

 

есть

 

Y

р

i

 

Y

а

i

  

P

i

 = 

—

, 

Q

i

 = 

—

, (26)

 

n

y

 

n

y

 

 

Y

р

k

 

 

Y

а

k

 

k 

≠

 

i

 

k 

≠

 

i

где

 

Y

a

 = 1/

R

 — 

активная

 

проводимость

 

ветвей

 

кон

-

тура

; 

R

 — 

активное

 

сопротивление

 

ветвей

 

контура

;

Y

р

 = 1/

X

 —

реактивная

 

проводимость

 

ветвей

 

контура

; 

X

 — 

реактивное

 

сопротивление

 

ветвей

 

контура

.

При

 

этом

 

в

 

расчетах

 

сопротивления

 

всех

 

ветвей

 

контура

 

приводятся

 

к

 

единому

  (

высшему

) 

напряже

-

нию

.

Предельный

 

по

 

статической

 

устойчивости

 

поток

 

активной

 

мощности

 

по

 

ветви

 «

i

–

j

», 

входящей

 

в

 

рас

-

четное

 

сечение

, 

можно

 

определить

 

по

 

известному

 

выражению

:

 

U

i 

U

j

 

P

i 

– 

j

 = 

— 

sin 



i 

– 

j

, (27)

 

X

i 

– 

j

где

 

X

i 

– 

j

  — 

приведенное

 

к

 

ВН

 

реактивное

 

сопротив

-

ление

 

ветви

  «

i

–

j

», 

входящей

 

в

 

расчетное

 

сечение

; 

U

i

 

и

 

U

j

 — 

модули

 

напряжений

 

по

 

концам

 

ветви

 «

i

–

j

»; 



i 

– 

j

— 

угол

 

передачи

 

мощности

 

по

 

ветви

 «

i

–

j

».

При

 



i 

– 

j

 = 90° 

выражение

 (27) 

принимает

 

значение

 

U

i 

U

j

 

P

i 

– 

j

 = 

—

. (28)

 

X

i 

– 

j

Поскольку

 

в

 

неоднородном

 

сечении

 

приведен

-

ные

 

реактивные

 

сопротивления

 

ветвей

 

низшего

 

напряжения

 

при

 

одинаковой

 

протяженности

 

входя

-

щих

 

в

 

сечение

 

ветвей

 

всегда

 

будет

 

выше

 

сопротив

-

лений

 

ветвей

 

более

 

высоких

 

напряжений

, 

то

 

пре

-

дел

 

передаваемой

 

по

 

ветвям

 

сечения

 

мощности

 

в

 

первую

 

очередь

 

будет

 

достигнут

 

на

 

ветви

 

низшего

 

напряжения

 

с

 

максимальным

 

приведенным

 

напря

-

жением

.

Рассмотрим

 

конкретный

 

пример

 

на

 

основе

 

схемы

, 

изображенной

 

на

 

рисунке

 2.

Рис

. 2. 

Схема

 

расчетного

 

сечения

 

сети

 

с

 

ветвями

 500–220 

кВ

: 

P

Г

 

и

 

Q

Г

 — 

активная

 

и

 

реактивная

 

генерирующая

 

мощ

-

ность

; 

P

Н

 

и

 

Q

Н

  — 

активная

 

и

 

реактивная

 

нагрузка

; 

Q



 — 

потери

 

реактивной

 

мощности

 

на

 

намагничивание

 

в

 

транс

-

форматорах

; 

Q

C

 — 

зарядная

 

мощность

 

ЛЭП

P

Н

 + 

J

 

(

Q

Н

 – 

Q

C

) + 

jQ



P

Г

 + 

J

 

(

Q

Г

 + 

Q

C

) – 

jQ



Ветвь

 500 

кВ

Ветвь

 220 

кВ

№

 3 (42) 2017

50

В

 

таблице

 1 

приведены

 

парамет

-

ры

 

ЛЭП

 

и

 

трансформаторов

, 

вхо

-

дящих

 

в

 

сеть

 

на

 

рисунке

 2, 

а

 

в

 

та

-

блице

 2 — 

параметры

 

элементов

 

самой

 

сети

 

при

 

протяженности

 

ЛЭП

 

500 

и

 220 

кВ

 

по

 500 

км

 

каждая

.

Суммарная

 

генерирующая

 

мощ

-

ность

 

в

 

сети

 

изменяется

 

в

 

диапа

-

зоне

 

от

 300 

до

 1000 

МВт

 

с

 

коэффи

-

циентом

 

мощности

 

соответственно

 

cos

Г



= 0,990–0,999.

Табл

. 1. 

Удельные

 

параметры

 

ветвей

 

схемы

Ветвь

(

Авто

)

трансформаторы

*

ЛЭП

R

0

, 

Ом

X

0

, 

Ом

Q

, 

МВар

R

0

, 

Ом

/

км

X

0

, 

Ом

/

км

Q

С

, 

МВар

Ветвь

 500 

кВ

0,28

29,2

3,753

0,0193

0,304

1,005

Ветвь

 220 

кВ

0,6

25,7

1,125

0,058

0,413

1,147

* 

Автотрансформаторы

 500 

кВ

 

приняты

 

мощностью

 3 × 417 = 1251 

МВА

,

  

автотрансформаторы

 220 

кВ

 

приняты

 

мощностью

 250 

МВА

Табл

. 3. 

Удельные

 

потоки

 

активной

 

и

 

реактив

-

ной

 

мощности

 

по

 

ветвям

 

расчетного

 

сечения

Класс

напряжения

Доля

 

потока

P

 

в

 

сети

Доля

 

потока

Q

 

в

 

сети

500 

кВ

0,8753

0,9395

220 

кВ

0,1247

0,0605

Табл

. 2. 

Расчетные

 

показатели

 

ветвей

 

схемы

 500–220 

кВ

Ветвь

(

Авто

)

трансформаторы

*

ЛЭП

Ветвь

 (

ЛЭП

 + 2 × 

АТ

)

R

0

, 

Ом

X

0

, 

Ом

Q

, 

МВар

L

ЛЭП

, 

км

R

0

, 

Ом

X

0

, 

Ом

Q

С

, 

МВар

R

0

, 

Ом

X

0

, 

Ом

Q

С

, 

МВар

Ветвь

 500 

кВ

0

0

0

500

9,65

152

502,5

9,65

152,1

502,5

Ветвь

 220 

кВ

3,099

132,7

4,501

500

149,79

1066,63

73,5

149,79

1066,6

73,5

Итого

—

—

—

—

159,44

1218,63

576

159,44

1218,6

576,0

* 

Количество

 

автотрансформаторов

 — 2 × 220 

кВ

. 

Все

 

напряжения

 

приведены

 

к

 

напряжению

 500 

кВ

Табл

. 4. 

Динамика

 

изменения

 

потоков

 

мощности

 

и

 

углов

 

передачи

 

по

 

ветвям

 

расчетного

 

сечения

Ветвь

Генерация

Поток

 

активной

 

мощ

-

ности

, 

МВт

Поток

 

реактив

-

ной

 

мощ

-

ности

, 

МВт

sin

 



 

пере

-

дачи

Угол

 

пере

-

дачи

, 

 

град

Базо

-

вое

 

напря

-

жение

, 

кВ

Потери

напряжения

, 

кВ

Нап

 

ря

-

же

 

ние

на

 

вы

-

ходе

,

кВ

Активная

 

мощность

Реактивная

 

мощ

 

ность



U'



U"

Ветвь

 500 

кВ

300

60.9

255,2

128,4

0,2371

13,71

500,0

59,23

104,78

453,05

Ветвь

 220 

кВ

44,8

38,3

0,2646

15,34

500,0

105,60

95,68

405,84

Ветвь

 500 

кВ

400

73.1

340,3

139,8

0,3138

18,29

500,0

65,78

140,34

456,34

Ветвь

 220 

кВ

59,7

39,1

0,3496

20,46

500,0

111,99

131,25

409,61

Ветвь

 500 

кВ

500

81.3

425,4

147,5

0,3858

22,70

500,0

70,75

175,99

463,93

Ветвь

 220 

кВ

74,6

39,6

0,4292

25,42

500,0

117,79

166,89

417,06

Ветвь

 500 

кВ

600

85.6

510,5

151,5

0,4517

26,85

500,0

74,17

211,71

475,56

Ветвь

 220 

кВ

89,5

39,9

0,5019

30,12

500,0

122,99

202,61

428,00

Ветвь

 500 

кВ

700

85.9

595,5

151,8

0,5105

30,69

500,0

76,04

247,50

490,92

Ветвь

 220 

кВ

104,5

39,9

0,5583

33,94

500,0

127,61

250,60

448,86

Ветвь

 500 

кВ

800

82.4

680,6

148,5

0,5619

34,19

500,0

76,38

283,37

509,66

Ветвь

 220 

кВ

119,4

39,7

0,6236

38,58

500,0

131,64

274,27

459,26

Ветвь

 500 

кВ

900

66.5

765,7

133,6

0,6032

37,10

500,0

71,87

319,47

534,19

Ветвь

 220 

кВ

134,3

38,7

0,6712

42,16

500,0

133,82

310,38

480,02

Ветвь

 500 

кВ

1000

63.7

850,8

131,0

0,6440

40,09

500,0

72,49

355,32

555,89

Ветвь

 220 

кВ

149,2

38,5

0,7146

45,61

500,0

137,96

346,23

500,94

Распределение

 

мощности

 

по

 

ветвям

 

схемы

 

соглас

-

но

 (26) 

характеризуется

 

данными

 

таблицы

 3, 

из

 

которой

 

следует

, 

что

 87,5 % 

всей

 

мощности

, 

входящей

 

в

 

рассмат

-

риваемое

 

сечение

, 

передается

 

по

 

сети

 500 

кВ

, 

а

 12,5 % — 

по

  

сети

 220 

кВ

.

Параметры

 

передачи

 

мощности

 

по

 

сети

 

в

 

диапазоне

 

300–1000 

МВт

 

характеризуются

 

данными

 

таблице

 4.

УПРАВЛЕНИЕ

СЕТЯМИ

51

Из

 

приведенной

 

таблицы

 

видно

, 

что

 

во

 

всем

 

диапазоне

 

передаваемой

 

по

 

сечению

 

мощности

 

угол

 

передачи

 

по

 

ЛЭП

 220 

кВ

 

остается

 

выше

, 

чем

 

по

 

ЛЭП

 

500 

кВ

. 

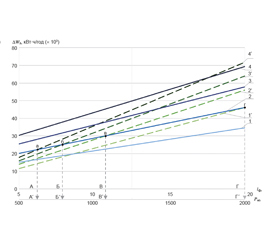
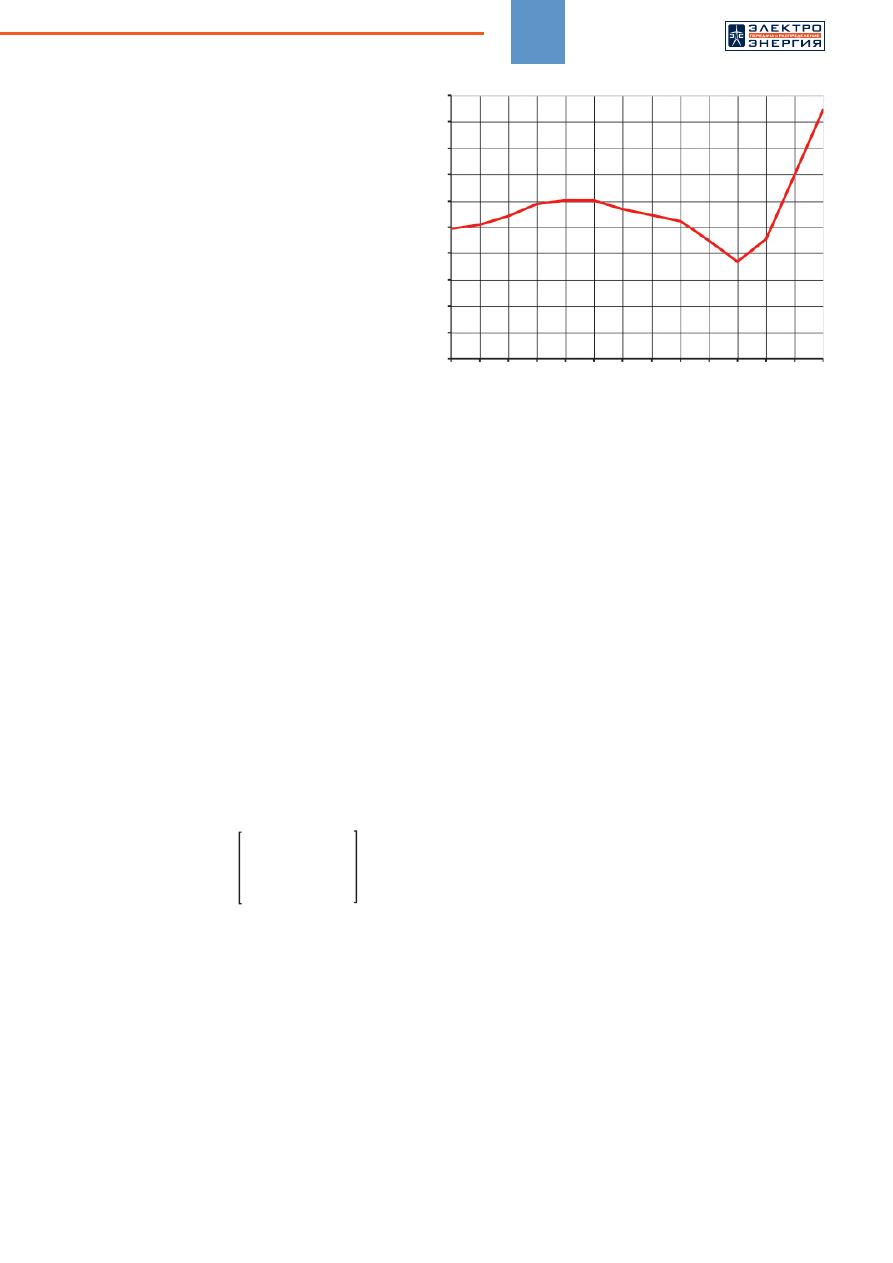
Динамика

 

соотношения

 

углов

 

передачи

 

по

 

ветвям

 220 

и

 500 

кВ

 

при

 

увеличении

 

передаваемой

 

по

 

сечению

 

мощности

 

представлена

 

на

 

рисунке

 3.

Из

 

приведенного

 

на

 

рисунке

 3 

гра

-

фика

 

следует

, 

что

 

по

 

мере

 

роста

 

потока

 

мощности

 

и

 

угла

 

передачи

 

мощности

 

по

 

ветви

 220 

кВ

 

проявляется

 

устойчивая

 

тенденция

 

к

 

опережению

 

угла

 

передачи

 

по

 

ветви

 500 

кВ

, 

то

 

есть

 

растет

 

вероят

-

ность

 

опережающего

 

достижения

 

пере

-

дачи

 

мощности

 

по

 

ветви

 

низшего

 

на

-

пряжения

 

или

, 

в

 

общем

 

случае

, 

по

 

ветви

 

с

 

большим

 

реактансом

.

Проведенный

 

анализ

 

позволяет

 

сделать

 

ряд

 

важных

 

выводов

, 

меняю

-

щих

 

современные

 

принципы

 

управле

-

ния

 

статической

 

устойчивостью

:

1) 

с

 

увеличением

 

потока

 

мощности

 

по

 

некоторому

 

неоднородному

 

сечению

 

предел

 

статической

 

устойчивости

 

энергосистемы

 

наступает

 

при

 

до

-

стижении

 

угла

 

передачи

 

мощности

 

значения

 

90° 

по

 

ЛЭП

 

с

 

наибольшим

 

относительным

 

реак

-

тансом

 (

модель

 «

слабейшего

 

звена

»);

2) 

при

 

достижении

 

предела

 

статической

 

устой

-

чивости

 

системы

 

по

 

критерию

 

перемены

 

зна

-

ка

 

якобиана

 

в

 

сети

 

обязательно

 

найдется

 

хоть

 

одна

 

ЛЭП

 

с

 

максимальным

 

углом

 

передачи

, 

которая

 

обязательно

 

входит

 

в

 

состав

 

наиболее

 

опасного

 

сечения

 

независимо

 

от

 

его

 

структуры

;

Управление

 

статической

 

устойчивостью

 

и

 

ввод

 

системы

 

в

 

допустимую

 

по

 

устойчивости

 

область

 

с

 

заданным

 

коэффициентом

 

запаса

 

можно

 

осуще

-

ствить

 

по

 

следующему

 

алгоритму

:

1. 

Представим

 

якобиан

 

системы

 

уравнений

 

уста

-

новившегося

 

режима

 (18) 

как

 

функцию

 

вектора

 

генерирующих

 

мощностей

 

в

 

узлах

 

системы

  

.

P

Г

:  

 

∂



( 

.

P

Г

)

' 

∂



( 

.

P

Г

)

'

 

—  —

 

∂



 

∂

U

 

D

(n

y

)

 

= 

f

( 

.

P

Г

) =

 

det

                                

. (29)

 

∂



( 

.

P

Г

)

" 

∂



( 

.

P

Г

)

"

 

—  —

 

∂



 

∂

U

2. 

Используя

 

метод

 

проекции

 

градиента

 [5], 

мини

-

мизируем

 

функцию

 (29) 

до

 

достижения

 

ею

 

нуле

-

вого

 

значения

 

по

 

кратчайшему

 

пути

, 

что

 

будет

 

соответствовать

 

пределу

 

статической

 

устойчи

-

вости

.

3. 

Выявим

 

k

–

ю

 

ветвь

 

расчетной

 

схемы

 

электриче

-

ской

 

сети

 

с

 

максимальным

 

углом

 

передачи

 

мощ

-

ности

 



k

 (

угол

 

передачи

 

мощности

 

по

 

k

-

й

 

ветви

), 

определим

 

поток

 

активной

 

мощности

 

по

 

ней

, 

вычислим

 

с

 

использованием

 

матриц

 [

Y

] 

и

 [

X

] 

ко

-

эффициенты

 

влияния

 

мощностей

 

в

 

узлах

 

i

 

на

 

поток

 

мощности

 

по

 

k

-

й

 

ветви

 

и

 

определим

 

зна

-

чения

 

генерирующих

 

мощностей

 

в

 

узлах

  

.

P

Г

i

, 

при

 

которых

 

поток

 

мощности

 

в

 

рассматриваемой

 

k

-

й

 

ветви

 

уменьшится

 

на

 

величину

 

нормативно

-

го

 

запаса

 

статической

 

устойчивости

 

k

з

ст

.

у

: 

Поток

 

активной

 

мощности

, 

тыс

. 

МВт

1,22

1,20

1,18

1,16

1,14

1,12

1,10

1,08

1,06

1,04

1,02

3,0

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

2,0

2,2

2,4

2,6

2,8

Соо

тношение

 

уг

лов

 

пере

да

чи

мощ

 

ности

 

по

 

вх

одящим

 

в

 

се

чение

 

ВЛ

 

220 

и

 500 

кВ

 

в

 

сост

ав

е

 

се

чения

, 

от

н

. 

ед

.

Рис

. 3. 

Соотношение

 

углов

 

передачи

 

мощности

 

по

 

ветвям

 220 

и

 500 

кВ

 

в

 

зависимости

 

от

 

величины

 

передаваемой

 

мощности

 

P

k

доп

 = 

P

k

пред

 / (1 + 

k

з

ст

.

у

), (30)

где

 

P

k

пред

 — 

предельный

 

переток

 

с

 

максимальным

 

значением

 

угла

 

передачи

 

мощности

 

по

 

k

-

й

 

ветви

 

схемы

, 

соответствующий

 

нулевому

 

значению

 

яко

-

биана

; 

P

k

доп

 — 

допустимый

 

предел

 

передачи

 

мощ

-

ности

 

по

 

k

-

й

 

ветви

 

с

 

учетом

 

нормативного

 

запаса

 

статической

 

устойчивости

. 

Поиск

 

искомого

 

реше

-

ния

 

можно

 

осуществлять

 

методом

 

проекции

 

гра

-

диента

 [5].

Если

 

при

 

заданных

 

максимальных

 

нагрузках

 

в

 

узлах

 

не

 

удается

 

найти

 

искомого

 

решения

 

из

-

менением

 

режимов

 

работы

 

электростанций

, 

то

 

следует

 

ввести

 

ограничения

 

нагрузок

, 

используя

 

функцию

 

удельных

 

ущербов

 

от

 

степени

 

ограниче

-

ния

 

нагрузки

 

и

 

метод

 

неопределенных

 

множите

-

лей

 

Лагранжа

 [7–9].

ВЫВОДЫ

1. 

В

 

расчетах

 

надежности

 

энергосистем

 

и

 

их

 

ма

-

гистральных

 

сетей

 

наиболее

 

эффективным

 

методом

 

учета

 

статической

 

устойчивости

 

явля

-

ется

 

использование

 

критерия

 

перемены

 

знака

 

якобиана

 

системы

 

уравнений

 

установившегося

 

режима

 

в

 

сочетании

 

с

 

вводом

 

режима

 

в

 

до

 

пус

-

ти

 

мую

 

область

.

2. 

При

 

вводе

 

режима

 

в

 

допустимую

 

по

 

устойчиво

-

сти

 

область

 

используется

 

принцип

 

определе

-

ния

 «

слабейшего

 

звена

» 

в

 

виде

 

ЛЭП

 

с

 

наиболь

-

шим

 

углом

 

передачи

 

при

 

доведении

 

режима

 

до

 

близкого

 

к

 

нулю

 

значения

 

якобиана

, 

который

 

рассматривается

 

как

 

функция

 

вектора

 

генери

-

рующих

 

мощностей

.

3. 

В

 

предлагаемой

 

методике

 

для

 

управления

 

ста

-

тической

 

устойчивостью

 

энергосистемы

 

ре

-

комендуется

 

использовать

 

принцип

 

перерас

-

пределения

 

нагрузок

 

между

 

генерирующими

 

мощностями

 

в

 

сочетании

 

с

 

целенаправленным

 

ограничением

 

нагрузок

 

потребителей

 

по

 

крите

-

рию

 

минимума

 

ущерба

 

экономике

 

с

 

использова

-

нием

 

неопределенных

 

множителей

 

Ла

 

гранжа

.

№

 3 (42) 2017

52

Издательство

 

журнала

 «

ЭЛЕКТРОЭНЕРГИЯ

. 

Передача

 

и

 

распределение

»

выпустило

 

книгу

 

академика

 

РАЕН

, 

профессора

 

В

. 

А

. 

НЕПОМНЯЩЕГО

Тираж

 

книги

 5000 

экз

., 

объем

 196 

с

., 

формат

 170

х

235 

мм

.

Для

 

приобретения

 

издания

 

необходимо

 

позвонитпо

 

многоканальному

 

телефону

 +7 (495) 645-12-41 

или

 

написать

 

по

 e-mail: [email protected]

В

 

монографии

 

исследована

 

надежность

 

оборудования

 

элек

 

тростанций

 

и

 

электрических

 

сетей

 

напряжением

 

1150–10(6) 

кВ

, 

разработана

 

методика

 

сбора

 

и

 

статисти

-

ческой

 

обработки

 

информации

 

о

 

надежности

 

оборудо

-

вания

. 

На

 

основе

 

статистических

 

данных

 

и

 

расчетов

 

определены

 

основные

 

параметры

 

надежности

 

и

 

ди

-

намика

 

их

 

изменения

 

в

   

процессе

 

эксплуатации

. 

Вы

-

явлены

 

статистические

 

законы

 

распределения

 

отказов

 

и

 

времени

 

восстановления

 

элементов

 

энергосистем

. 

Проведено

 

их

 

сравнение

 

с

 

зарубежными

 

данными

.

4. 

Аварийные

 

ситуации

 

с

 

нарушениями

 

стати

-

ческой

 

устойчивости

, 

особенно

 

приводящие

 

к

 

ограничениям

 

нагрузок

, 

целесообразно

 

про

-

верить

 

более

 

точными

 

методами

, 

чтобы

 

избе

-

жать

 

излишних

 

нарушений

 

электроснабжения

 

потребителей

. 

5. 

Предлагаемая

 

методика

 

оценки

 

статической

 

устойчивости

 

энергосистемы

 

и

 

управления

 

ею

 

не

 

предполагает

 

замену

 

традиционных

 

подходов

 

к

 

расчетам

 

устойчивости

 

методом

 

утяжеления

 

с

 

контролем

 

перетоков

 

мощности

 

по

 

критическим

 

сечениям

 

в

 

задачах

, 

связанных

 

с

 

разработкой

 

систем

 

противоаварийной

 

автоматики

 

и

 

ее

 

экс

-

плуатацией

, 

но

 

дает

 

возможность

 

более

 

коррек

-

тно

 

сформировать

 

круг

 

возможных

 

аварийных

 

состояний

 

магистральных

 

электрических

 

сетей

, 

приводящих

 

к

 

нарушениям

 

статической

 

устойчи

-

вости

.  

ЛИТЕРАТУРА

1. 

Методические

 

указания

 

по

 

устойчи

-

вости

 

энергосистем

. 

Утв

. 

приказом

 

Минэнерго

 

России

 

от

 30.06.2003 

№

 277.

2. 

Stott B. Decompled Newton Load 
Flow. IEEE trans power appar. and 
syst. Vol. PAS 91, p.1955–1959. 
Sept/Okt., 1972. 

3. 

Фазылов

 

Х

.

Ф

., 

Насыров

 

Т

.

Х

. 

Уста

-

новившиеся

 

режимы

 

электроэнер

-

гетических

 

систем

 

и

 

их

 

оптими

-

зация

. 

Ташкент

: 

Изд

-

во

  «

Молик

», 

1999. 370 

с

.

4. Uemira  K.  Approcsimated  Jacobians 

in Newtons Power Flow Method. 
PSCC, Proceedings Grenoble, 1972.

5. 

Химмельбдау

 

Д

.

М

. 

Прикладное

 

не

-

линейное

 

программирование

. 

Пер

. 

с

 

англ

. 

Под

 

ред

. 

М

.

Л

. 

Быховского

. 

М

.: 

Мир

, 1975. 534 

с

.

6. 

Горев

 

А

.

А

. 

Избранные

 

труды

 

по

 

вопросам

 

устойчивости

 

электриче

-

ских

 

систем

. 

М

.–

Л

.: 

ГЭИ

, 1960. 

С

. 

227–250.

7. 

Непомнящий

 

В

.

А

. 

Экономические

 

проблемы

 

повышения

 

надежности

 

электроснабжения

. 

Ташкент

: 

Изд

-

во

  «

ФАН

» 

Академии

 

Наук

 

Респуб

-

лики

 

Узбекистан

, 1985. 200 

с

.

8. 

Непомнящий

 

В

.

А

. 

Экономические

 

потери

 

от

 

нарушений

 

электроснаб

-

жения

. 

М

.: 

Издательский

 

дом

 

МЭИ

, 

2010. 188 

с

.

9. 

Непомнящий

 

В

.

А

. 

Агрегированные

 

значения

 

удельных

 

ущербов

 

от

 

нарушений

 

электроснабжения

 // 

Энергорынок

, 2014, 

№

 9. 

С

. 36–47.

REFERENCES

1. SO 153-34.20.576-2003. Methodolo-

gy guidelines for power systems sta-
bility. Moscow, NTs ENAS Publ., 
2004. 10 p. (in Russian)

2. 

Stott B. Decoupled Newton Load 
Flow. - IEEE Trans. Power Appar. 
and Syst. Sept./Oct., 1972, vol. 
PAS91. pp.1955–1959. 

3. 

Fazylov Kh. F., Nasyrov T. Kh. 
Ustanovivshiesya rezhimy elektroen-
ergeticheskikh sistem i ikh optimizat-
siya [Power systems steady-state 
modes and optimization]. Tashkent, 
Molik Publ., 1999. 370 p.

4. Approximated Jacobians in Newtons 

Power Flow Method. PSCC, Pro-
ceedings. Grenoble, 1972.

5. Himmelblau D. M. Applied nonlinear 

programming. The University of Tex-
as, Austin, Texas, 1972. (Russ. ed.: 
Himmelblau D. M. Prikladnoe ne-
lineynoe programmirovanie. Mos-
cow, Mir Publ., 1975. 536 p.).

6. Gorev A.A. Izbrannye trudy po vo-

prosam ustoychivosti elektricheskikh 
sistem [Selected works associated 
with power systems stability]. Lenin-
grad, GEI Publ., 1960. 250 p.

7. 

Nepomnyashchiy V.A. Ekonomich-
eskie problemy povysheniya nadezh-
nosti elektrosnabzheniya [Economic 
problems associated with improve-
ment of power supply reliability]. 
Tashkent, FAN Publ., 1985. 200 p.

8. 

Nepomnyashchiy V.A. Ekonomich-
eskie poteri ot narusheniy elektrosna-
bzheniya [Economic losses due to 
interruptions of electric power sup-
ply]. Moscow, Izdatelskiy dom MEI 
Publ., 2010. 188 p.

9. Nepomnyashchiy  V.A.  Aggregated 

data of speci

fi

 c losses due to inter-

ruptions of electric power supply. En-
ergorynok [Energy market], 2014, 
no.9, pp. 36-47. (in Russian)

УПРАВЛЕНИЕ

СЕТЯМИ