Способ снижения потерь электроэнергии в распределительных сетях с двусторонним питанием

Page 1

Page 2

ЭНЕРГО-

ЭФФЕКТИВНОСТЬ

Способ снижения потерь
электроэнергии в распределительных
сетях с двусторонним питанием

УДК 621.316.7:621.3.017

статье

рассматривается

способ

снижения

потерь

городских

сельских

распредели

–

тельных

сетях

электроснабжения

выполненных

воздушными

линиями

электропередачи

двусторонним

питанием

оборудованными

реклоузерами

Предложена

математическая

модель

методика

алгоритм

определения

оптимальных

точки

зрения

минимизации

потерь

мест

нормальных

разрывов

осуществляемых

реклоузерами

Рохлов

инженер 2 категории

отдела перспективного

развития филиала

АО «Россети Тюмень» —

Тюменские электри-

ческие сети

Хмара

к.т.н., доцент,

заведующая кафедрой

электроэнергетики

ФГБОУ ВО «Тюменский

индустриальный

университет»

Бойчук

начальник отдела

перспективного развития

филиала АО «Россети

Тюмень» — Тюменские

электрические сети

Ключевые

слова

распределительные

сети, реклоузер, потери

электроэнергии, потери

мощности

о итогам реализации Страте-

гии развития электросетевого

комплекса Российской Феде-

рации, утвержденной распо-

ряжением Правительства Российской

Федерации от 03.04.2013 № 511-р [1]

(далее — Стратегия) удалось снизить

уровень фактических потерь электро-

энергии от отпуска электрической

энергии в сеть с 11,8% в 2012 году до

10,4% в 2019 году, в то время как Го-

сударственная программа «Энергоэф-

фективность и развитие энергетики»

[2] предполагала снижение до уровня

в 9,2% к 2019 году.

Из сравнения фактических относи-

тельных потерь электроэнергии в элек-

трических сетях России с относитель-

ными потерями в сетях развитых стран

видно, что у России на текущий момент

есть существенный потенциал для сни-

жения потерь. По различным оценкам

потенциал снижения технических по-

терь составляет 3–5 млрд кВт·ч/год.

Доля потенциала снижения потерь

в сетях различных распределительных

сетевых компаний и территориальных

сетевых организаций варьируется от

10 до 40 % [3–5].

Следовательно, на текущий мо-

мент снижение уровня потерь элек-

трической энергии в сетях среднего

и низкого напряжения является акту-

альной научно-технической задачей

для электросетевого комплекса. Це-

лью данной работы является выявле-

ние потенциала снижения затрат на

передачу электроэнергии в городских

и сельских распределительных сетях

электроснабжения с двусторонним пи-

танием, представленных воздушными

линиями электропередачи, оборудо-

ванными реклоузерами. Для достиже-

ния поставленной цели были решены

следующие задачи:

1. Формализован подход к составле-

нию задачи оптимизации режимов

работы распределительной сети

электроснабжения с двусторонним

питанием, представленной воздуш-

ными линиями электропередачи,

оборудованными реклоузерами по

критерию минимизации потерь элек-

трической энергии при ее передаче.

2. Разработан алгоритм решения ма-

тематической задачи оптимизации

мест нормальных разрывов реклоу-

зерами.

3. Проведено имитационное моде-

лирование работы предложенного

алгоритма на примере участка рас-

пределительной сети с двусторон-

ним питанием для выявления потен-

циала снижения затрат на передачу

электроэнергии.

Согласно Стратегии, одной из при-

чин высокого уровня потерь электро-

энергии является неоптимальность

режимов работы электрических сетей.

Для оптимизации режимов работы се-

тей необходимо принимать соответ-

ствующие меры как на стадии плани-

рования развития, так и на стадии их

эксплуатации.

Для решения задач оптимизации

широко применяются оптимизационные

математические модели, позволяющие

отыскать экстремум целевой функции

на множестве, определенном системой

ограничений с помощью методов мате-

матического программирования. В ра-

ботах Буздко И.А. [6], Костина В.Н. [7],

Дале В.А. [8] рассмотрены основные

оптимизационные задачи управления

режимами электроэнергетических сис-

тем и методы их решения.

Page 3

К задачам оптимального планирования развития

распределительных электрических сетей относит-

ся определение оптимальных параметров электро-

передачи, таких как сечения проводников и уровни

напряжения. Авторами Шнеллем Р.В. и Картавце-

вым В.В. [9], Решетовым С.А. [10], Латыповым И.С.,

Сушковым В.В. и Хмарой Г.А. [11] предложены реше-

ния в этой области, применимые на стадии проекти-

рования систем электроснабжения.

На стадии эксплуатации электрической сети од-

ним из способов оптимизации режимов работы

является оптимальное управление сетью. Для по-

строения законов управления режимами работы

электрических сетей также широко используются ма-

тематические модели.

В статье [12] описана методика определения оп-

тимальных параметров устройств компенсации реак-

тивной мощности для внедрения устройств FACTS,

основанная на применении генетического алгоритма

при решении оптимизационной задачи. Для прием-

лемости получаемых решений накладываются огра-

ничения на емкостную мощность узла, коэффици-

енты мощности вводного и потребительских узлов

и чистую приведенную стоимость.

В работе [13] Чмутовым А.П. рассматривается оп-

тимизация режимов работы коммунальных распре-

делительных сетей по напряжению с использовани-

ем положений теории линейных неравенств.

В статье [14] рассмотрена оптимизационная

модель двухуровневой активно-адаптивной элек-

трической сети с распределенной генерацией, поз-

воляющая достигнуть максимального дохода при

минимальных эксплуатационных затратах с учетом

выгод многих заинтересованных сторон. Для реше-

ния оптимизационной модели применяется метод

ADMM.

В работе [15] предложен алгоритм оптимизации

потоков реактивной мощности в активно-адаптивных

электрических сетях по критерию минимума потерь

активной мощности, разработанный с применением

метода ADMM.

В городских и сельских распределительных элек-

трических сетях широкое распространение получи-

ли воздушные линии (ВЛ) с двусторонним питанием.

Как правило, ВЛ с двусторонним питанием эксплу-

атируют в разомкнутом режиме. Согласно п. 5 РД

34.09.254 [16] оптимизация мест размыкания линий

6–35 кВ с двусторонним питанием является одним из

наиболее эффективных организационных меропри-

ятий по оптимизации режимов работы и, как след-

ствие, снижению потерь электроэнергии в распреде-

лительных электрических сетях.

Современные пункты секционирования, такие как

реклоузеры, имеют функцию дистанционного управ-

ления [17]. Это позволяет при определении оптималь-

ного места разрыва вместо расчета потерь электро-

энергии производить расчет потерь мощности, а также

избавиться от необходимости прогнозирования, по-

скольку расчет и смена мест нормальных разрывов

производится в реальном времени. Как следствие,

существенно повышается точность вычислений и сни-

жается уровень технических потерь в сети.

В работах [18, 19, 20] рассмотрены способы опре-

деления оптимальных мест нормальных разрывов.

Однако применение данных способов невозможно,

поскольку они не учитывают резервы мощности цен-

тров питания.

При выборе оптимального места нормального

разрыва необходимо учитывать резервы мощно-

сти питающих подстанций, так как при организации

разрыва в оптимальном месте одна из подстанций

может оказаться перегруженной. Установлено, что

существует два варианта разгрузки питающих под-

станций: перемещение места разрыва в сторону

смежной подстанции по рассматриваемой линии

либо разгрузка по одной из других линий с двусто-

ронним питанием. При этом также следует учитывать

резервы мощности центров питания, на которые про-

изводится перевод нагрузки с перегруженной под-

станции. При выборе варианта разгрузки подстанций

необходимо руководствоваться минимизацией по-

терь электроэнергии в сети. Следовательно, необ-

ходимо определять комбинации оптимальных мест

разрывов для сети в целом, а не для каждой линии

в отдельности, и учитывать при этом ограничения

в питающих узлах.

Для формализации задачи оптимизации режимов

работы распределительной сети электроснабжения

с двусторонним питанием, представленной воздуш-

ными линиями электропередачи, оборудованными

реклоузерами, по критерию минимизации потерь

электрической энергии при ее передаче рассмотрим

электрическую сеть, состоящую из

подстанций.

Каждой подстанции присвоим свой порядковый но-

мер 1…

. Введем булевы переменные, задающие

состояние реклоузера №

, установленного на

-й ли-

нии, связывающей подстанции



(

)

–

= 1 — реклоузер разомкнут,



(

)

–

= 0 — реклоузер замкнут.

(1)

Обозначим через



суммарное количество ре-

клоузеров на всех линиях.

Введем множество

— множество всех



—

мерных булевых векторов

, то есть векторов, коор-

динаты которых могут принимать значения 0 или 1.

Применительно к поставленной задаче это множе-

ство будет задавать все возможные комбинации со-

стояний реклоузеров.

Поскольку для нормального функционирования

сети необходимо, чтобы на каждой линии был толь-

ко один разрыв, и при этом ни одна подстанция не

была перегружена, следует определить множество

‘

векторов — комбинаций состояний реклоузе-

ров, удовлетворяющих этим ограничениям.

Таким образом, для отыскания оптимального век-

тора

необходимо решить несколько задач:

1. Определить множество

‘.

2. Определить зависимость потерь мощности



(

3. Подобрать алгоритм, позволяющий определить

вектор

, соответствующий минимуму целевой

функции



(

) на множестве

‘.

Множество

‘ задается системой ограничений, ис-

ходя из двух условий:

№

4 (67) 2021

Page 4

100

– ни одна из подстанций в рассматриваемой сети

не должна быть перегружена;

– на каждой линии должен быть строго один разрыв.

Следует отметить, что реклоузеры, разрывы на

которых приводят к перегрузке проводов ЛЭП или

оборудования в линейных ячейках питающих под-

станций, необходимо исключить из рассмотрения, по-

скольку разгрузить указанные элементы переключе-

ниями в смежной сети не представляется возможным.

Ограничения на загрузку подстанций задаются

системой неравенств, в которой каждой подстанции

соответствует свое неравенство вида:

д.п.отп.

≤

д.п.рез.

(2)

где

д.п.отп.

— мощность, отпускаемая по фидерам

с двусторонним питанием при данной комбинации

разрывов;

д.п.рез.

— мощность, отведенная фидерам

с двусторонним питанием.

Мощность, отведенная фидерам с двусторонним

питанием, определяется следующим образом:

д.п.рез.

N –

ДДТН

– S

о.п.

(3)

где

N –

— мощность подстанции в режиме

N –

ДДТН

— коэффициент длительно допустимой токо-

вой нагрузки, определяемый по Приказу Минэнерго

РФ от 08.02.2019 №81 [21];

о.п.

— мощность, отпу-

скаемая по фидерам с односторонним питанием.

Мощность

д.п.отп.

, отпускаемая по фидерам с дву-

сторонним питанием, рассчитывается как сумма

мощностей, отпускаемых по каждому фидеру с дву-

сторонним питанием в отдельности:

д.п.отп.

д.п.отп.1

д.п.отп.2

+ … +

д.п.отп.

(4)

где

д.п.отп.

— мощность, отпускаемая по

i –

й линии;

— количество линий с двусторонним питанием, за-

питанных от рассматриваемой подстанции.

Поскольку мощность, отпускаемая по линии, за-

висит от положения места разрыва, каждому рекло-

узеру поставим в соответствие доли, на которые он

делит суммарную мощность потребителей линии.

Таким образом, зависимость мощности, отпускаемой

по линии, задается следующим образом:

д.п.отп.

д.п.потр.

· (



+ … +



), (5)

где

д.п.потр.

— суммарная мощность потребителей

-й

линии;

— количество реклоузеров, установлен-

ных на

-й линии;

— доля мощности со стороны

рассматриваемой подстанции при разрыве на

-м

реклоузере;



— булева переменная, задающая со-

стояние

-го реклоузера.

Поскольку на линии может быть только один раз-

рыв, набор переменных, соответствующий опре-

деленному месту разрыва, содержит только одну

переменную, равную единице. Таким образом, под-

ставляя такой набор переменных в соотношение (5),

все слагаемые (кроме одного в скобках) будут рав-

ны нулю, а оставшееся будет представлять из себя

долю суммарной мощности потребителей рассма-

триваемой линии со стороны рассматриваемой под-

станции, соответствующую разомкнутому реклоузе-

ру, умноженную на единицу.

Для составления системы ограничений по резер-

ву мощности подстанций введем некоторые обозна-

чения:

— мощность подстанции р, отведенная фи-

дерам с двусторонним питанием;

p – q

— количество

линий, связывающих подстанции

;

p – q

— суммар-

ная мощность потребителей

-й линии, связывающей

подстанции

;

p – q

— количество реклоузеров

в магистрали

-й линии, связывающей подстанции

;



(

)

–

— булева переменная, задающая состояние

реклоузера

, установленного на

-й линии, связыва-

ющей подстанции р и

;

(

)

–

(

) — доля суммарной

мощности потребителей

-й линии, связывающей

подстанции р и

, со стороны подстанции

, соответ-

ствующая реклоузеру

на линии

Используя соотношения (2) – (5) составим систе-

му ограничений по резерву мощности всех подстан-

ций рассматриваемой сети:

–

–N

 

–





(

)

–

(

)

–

(1) + … +



– N





(

)

–N

(

)

–N

(1) ≤

= 1

–

–N

 

–





(

)

–

(

)

–

(2) + … +



–N





(

)

–N

(

)

–N

(2) ≤

= 1

…

(6)

–N

(

N–

– N

(

N–

– N



–N





(

)

–N

(

)

–N

(

) + … +



(

N –

–N





(

)

(

N –

–N

(

)

(

N –

–N

(

) ≤

= 1

Также необходимо ввести ограничения, задаю-

щие единственность разрыва на линии:

–

1 ≤

≤







(

)

p – q

= 1

1 ≤

≤

(7)

= 1

1 ≤

≤

–

В левой части уравнений (7) выписывается сум-

ма переменных, задающих состояние реклоузеров,

установленных на одной линии. Поскольку только

один из них может быть разомкнут (только одна пе-

ременная в сумме может быть равной единице), вы-

писанные суммы должны быть равны одному.

Объединив системы (6) и (7) и добавив ограни-

чение на булевость переменных, получим итоговую

систему линейных уравнений и неравенств для за-

дания множества

A’

комбинаций разрывов, удовлет-

воряющих всем схемным и режимным ограничениям:

–

–N

 

–





(

)

–

(

)

–

(1) + … +



– N





(

)

–N

(

)

–N

(1) ≤

= 1

–

–N

 

–





(

)

–

(

)

–

(2) + … +



–N





(

)

–N

(

)

–N

(2) ≤

= 1

…

–N

(

N–

– N

(

N–

– N

 

–N





(

)

–N

(

)

–N

(

) + … +



(

N –

–N





(

)

(

N –

–N

(

)

(

N –

–N

(

) ≤

= 1

–

1 ≤

≤

 



(

)

p – q

= 1

1 ≤

≤

(8)

= 1

1 ≤

≤

–

1 ≤

≤

–

1 ≤

≤





(

)

p – q

∈

{0, 1}

1 ≤

≤

1 ≤

≤

–

1 ≤

≤

–

Целевая функция представляет собой зависи-

мость уровня потерь мощности в линиях от распо-

ЭНЕРГО-

ЭФФЕКТИВНОСТЬ

Page 5

101

ложения мест разрывов. Для одной линии данная

зависимость будет иметь вид:











+ … +





(9)

где



— потери мощности в линии при разрыве на

-м реклоузере.

Соотношение (9) представляет собой сумму про-

изведений булевых переменных, задающих поло-

жение реклоузеров на соответствующие им потери

мощности. Таким образом, при подстановке набора

переменных, отвечающих определенному месту раз-

рыва (только одна переменная в этом случае будет

равна единице), все потери, кроме одного значения,

обнулятся, а оставшиеся, соответствующие разом-

кнутому реклоузеру, будут умножены на 1.

Целевая функция для всей сети в целом пред-

ставляет собой сумму соотношений (9), составлен-

ных для каждой линии:

–









(

)

p – q



(

)

p – q

(10)

1 ≤

≤

= 1

1 ≤

≤

Следует отметить, что в соотношение (10) входят

только потери в магистральных участках линий, по-

скольку потери в отпайках не зависят от положения

места нормального разрыва.

Исходную задачу можно сформулировать следу-

ющим образом: найти булев вектор, обращающий

в максимум линейную функцию (9) на множестве ре-

шений системы (8). Решению таких задач посвящен

раздел математики — линейное целочисленное про-

граммирование.

Для решения сформулированной задачи опти-

мизации предложен симплекс-метод. Поскольку

решение, полученное симплекс-методом, может со-

держать дробные значения переменных, необходи-

мо применение специальных методов, позволяющих

получать целочисленные решения. Одним из наибо-

лее эффективных методов решения задач целочис-

ленного программирования является метод ветвей

и границ.

Метод ветвей и границ заключается в последо-

вательном разбиении (ветвлении) множества реше-

ний системы ограничений, вычислении оптимальных

значений целевой функции на каждом из полученных

после ветвления множеств (оценок) и выборе реше-

ния с наилучшей оценкой в качестве оптимального.

В данной работе для решения задач целочислен-

ного программирования выбран один из алгоритмов

метода ветвей и границ — алгоритм Лэнд и Дойг [22].

Таким образом, разработанная математическая

модель и предложенные методы решения позволя-

ют производить обоснованный выбор оптимальных,

с точки зрения минимизации потерь, мест нормаль-

ных разрывов в распределительной электрической

сети с соблюдением всех режимных и схемных огра-

ничений. Поскольку с ростом количества элементов

в рассматриваемой сети расчет становится трудо-

емким, имеет смысл его автоматизации. С этой це-

лью на основе разработанного алгоритма реализо-

ван программный комплекс на языке Visual Basic for

Applications, позволяющий производить выбор опти-

мальных мест нормальных разрывов в распредели-

тельной электрической сети 10 кВ [23].

Ïðåîáðàçîâàòåëè
èçìåðèòåëüíûå
íàïðÿæåíèÿ ÏÈÍ
îò 50 Â äî 3000 Â

Âûñîêîâîëüòíûå

ýëåêòðîííûå

êëåùè ÊÒ-1000-Â

äëÿ èçìåðåíèÿ òîêà

äî 1000 À ïðè

íàïðÿæåíèè íà

òîêîâîé øèíå

äî 10 000 Â

Ïðåîáðàçîâàòåëè èçìåðèòåëüíûå

ìîùíîñòè ñåðèè ÏÈÌ

äëÿ êîíòðîëÿ àêòèâíîé ìîùíîñòè

â äèàïàçîíå îò 1 äî 4000 êÂò

Ïðåîáðàçîâàòåëè èçìåðèòåëüíûå

òîêà ñåðèè ÏÈÒ äëÿ èçìåðåíèÿ òîêà

îò 40 ìÀ äî 25 000 À

Преобразователи

(

датчики

)

для

энергетиков

от

ООО

НПО

Горизонт

Плюс

C=…,

nnn

&mon

&c%!,ƒ%…2

ãĊ

“[

(

h“2!=

l%“*%”“*%L

Ëąã

C!,K%!/

“%K“2″

……%L

!=ƒ!=K%2*,

ąã

,ƒ

äË

…,

2%*=

…=C! ›

…,

=*2,”…%L

%?…%“2,.

%K!=ƒ%”=2

Ëã

“

!2,-,

,!%”=…/

“…

“

…/

“

c%“!

ËË

“2!

Ëą

“2=”

%“2%L…3

ƒ=

äË

…3

C%!2…/

=…=

“%%2…%

ĈË

…,

ĆË

…=

ćË

“2″%.

C=…,

nnn

&mon

&c%!,ƒ%…2

ãĊ

“[

%“3?

“2″

“C

=2…3

%“2=”*3

%K!=ƒ%”=2

ËãË

“%

““

ËĄ

,%…/

“

“2!=…/

qmc.

www.g

riz

ont-pl

us.ru

%K!=ƒ%”=2

Ëã

(

,*,)

“C

Ëć

,”=

ãĉ

“=…,

ćË

“*3

,ƒ%

“

…/

“/

…/

ĆË

%K…/L

“/

…%L

,…2

L“

(4$

`).

www.g

riz

ont-pl

us.ru

На прав

ах рек

ламы

№

4 (67) 2021

Page 6

102

Для иллюстрации предложенного алгоритма рас-

смотрим участок распределительной сети 10 кВ.

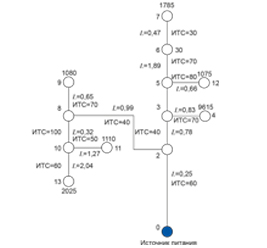
Схема сети показана на рисунке 1. Рассматривае-

мая сеть состоит из шести питающих подстанций

Рис

. 1.

Схема

примера

распределительной

сети

Рис

. 2.

Решение

загрузки

ЦП

Результаты

расчета

оптимального

варианта

напряжением 110/10 кВ и девяти воздушных линий

10 кВ с двусторонним питанием. Используя разрабо-

танный программный комплекс, проведем расчеты.

Результаты расчета представлены на рисунках 2 и 3.

ЭНЕРГО-

ЭФФЕКТИВНОСТЬ

Page 7

103

Рис

. 3.

Оптимальная

комбинация

разры

–

вов

Результаты

расчета

оптимального

варианта

Снижение потерь от применения предлагаемого ал-

горитма зависит от изначального положения нормаль-

ных разрывов. Для оценки снижения потерь в данной

работе были проанализированы все возможные ком-

бинации разрывов, не приводящие к перегрузке обо-

рудования в линейных ячейках питающих подстан-

ций, проводов ЛЭП и силовых трансформаторов. Все

комбинации были разбиты по группам в зависимости

от снижения потерь мощности, получаемого при пере-

ходе к оптимальной комбинации разрывов (рисунок 4).

Из показанной диаграммы видно, что переход

к оптимальной комбинации разрывов от большинства

комбинаций начальных положений разрывов приве-

дет к снижению потерь, равному от 10 до 40%. Сни-

жение потерь мощности при переходе от наихудшей

комбинации разрывов к оптимальной составит 43%.

ВЫВОДЫ

Проведенные исследования по оптимизации вы-

бора мест нормальных разрывов в городских

и сельских распределительных сетях электро-

снабжения с двусторонним питанием выявили

значительный потенциал к снижению затрат на

оплату потерь электроэнергии, возникающих при

ее передаче по ВЛ, оборудованным реклоузе-

рами. В приведенном примере снижение потерь

мощности при переходе от наихудшего варианта

к наилучшему составило 43%.

На следующем этапе следует рассмотреть

вопросы внедрения разработанного программного

комплекса и осуществить подбор технических

средств для реализации алгоритма на реальном

участке сети.

100

120

0-10%

10-20%

20-30%

30-40%

>40%

Количество комбинаций

Снижение потерь мощности при переходе

к оптимальной комбинации разрывов, %

Рис

. 4.

Диаграмма

снижения

потерь

мощности

от

применения

предла

–

гаемого

алгоритма

ЛИТЕРАТУРА

1. Распоряжение Правительства РФ

от 03.04.2013 № 511-р «Об утверж-

дении Стратегии развития электро-

сетевого комплекса». URL: http://

government.ru/docs/1220/.

2. Распоряжение Правительства РФ

от 03.04.2013 № 512-р «Об утверж-

дении государственной программы

Российской Федерации «Энерго-

эффективность и развитие энер-

гетики». URL: https://www.garant.ru/

products/ipo/prime/doc/70253012/.

3. Федеральная служба государ-

ственной статистики: официаль-

ный сайт. Москва. URL: https://

rosstat.gov.ru/enterprise_industrial.

4. World Bank Group. URL: http://data.

worldbank.org/indicator/EG.ELC.

LOSS.ZS.

5. Воротницкий В.Э. Энергосбереже-

ние и повышение энергетической

эффективности в электрических

сетях. М.: Теплоэнергетик, 2016.

336 с.

6. Буздко И.А., Васхнил Н.А., Ле-

вин М.С. Особенности оптимизаци-

онных задач энергетики и методов

их решения // Электричество, 1981,

№ 3. С. 1–7.

7. Костин В.Н. Оптимизационные

задачи электроэнергетики: учеб.

пособие. Санкт-Петербург: СЗТУ,

2003. 120 с.

8. Дале В.А., Кришан З.П., Паэгле О.Г.

Математические модели оптимиза-

ции развития сетей электроэнерге-

тических систем // Электричество,

1987, № 9. С. 1–6.

9. Шнелль Р.В., Картавцев В.В. Оп-

тимизация основных параметров

электропередачи // Электричество,

1982, № 4. С. 22–25.

10. Решетов С.А. Оптимизация элек-

трических сетей при заданной по-

тере напряжения // Электричество,

1982, № 6. С. 17–21.

11. Латыпов И.С., Сушков В.В., Хмара

Г.А. Разработка обобщенного под-

хода к выбору энергоэффективной

формы витого неизолированного

провода воздушной линии элек-

тропередачи класса напряжения

6–35 кВ // Промышленная энерге-

тика, 2020, № 1. С. 2–11.

12. Палау И.А.Г., Рамирез С.М., Бала-

банов М.С. [и др.]. Многофункци-

ональная оптимизация при ком-

пенсации реактивной мощности //

Известия Томского политехниче-

ского университета. Инжиниринг

георесурсов, 2018, т. 329, № 12.

С. 94–103.

13. Чмутов А.П. Оптимизация режима

напряжения в электрических рас-

пределительных сетях с использо-

ванием методов теории линейных

неравенств // Электрические стан-

ции, 1991, № 3. С. 62–66.

14. Liu Y., Liu S., Niu Z. Distributed Op-

timization for Active Distribution Net-

work Considering the Balance of

Multi-Stakeholder. URL: https://www.

mdpi.com/2227-9717/8/8/987.

15. Zheng W. A Fully Distributed Reac-

tive Power Optimization and Control

Method for Active Distribution Net-

works. URL: https://ieeexplore.ieee.

org/document/7042735.

16. РД 34.09.254. Инструкция по сни-

жению технологического расхода

электрической энергии на переда-

чу по электрическим сетям энерго-

систем и энергообъединений. Утв.

Министерством энергетики СССР

31.03.1986. М.: ВНИИЭ, 1986. 44 с.

№

4 (67) 2021

Page 8

104

17. Реклоузер вакуумный серии PBA/

TEL. ТШАГ 674153.101 ТИ. Тех-

ническая

информация.

URL:

http://tavrida-ua.com/products/

vacuumrecloser.html.

18. Булатов Б.Г., Тарасенко В.В. Алго-

ритмы интеллектуального управле-

ния режимом распределительной

сети // Вестник ЮУрГУ. Энергетика,

2012, № 37(296). С. 18–22.

19. Булатов Б.Г., Тарасенко В.В. Ал-

горитмы оптимальной реконфигу-

рации распределительной сети //

Вестник ЮУрГУ. Энергетика, 2013,

т. 13, № 2. С. 14–18.

20. Vai V., Suk S., Rathana R., Chhlonh C.

[at al]. Optimal Reconﬁ guration in

Distribution Systems with Distrib-

uted Generations Based on Modi-

ﬁ ed Sequential Switch Opening and

Exchange. URL: https://www.mdpi.

com/2076-3417/11/5/2146.

21. Приказ Минэнерго России от

08.02.2019 № 81 «Об утверждении

требований к перегрузочной спо-

собности трансформаторов и авто-

трансформаторов, установленных

на объектах электроэнергетики,

и ее поддержанию и о внесении

изменений в правила технической

эксплуатации электрических стан-

ций и сетей Российской Федера-

ции, утвержденные приказом Мин-

энерго России от 19 июня 2003 г.

№229». URL: https://www.garant.ru/

products/ipo/prime/doc/72109886/.

22. Land A.H., Doig A.G. An automatic

method of solving discrete program-

ming problems. Econometrica, 1960,

no. 3, pp. 497-520.

23. Рохлов В.А. Программа для ЭВМ:

Определение оптимальных, с точ-

ки зрения минимизации потерь,

мест нормальных разрывов в рас-

пределительной сети 6–10 кВ. А.с.

2021619480 РФ. Заявлено 16.04.21;

опубл. 10.07.21.

24. Логунов А.В., Рохлов В.А. Перспек-

тивы использования реклоузеров

в распределительных сетях / Ма-

териалы Национальной с между-

народным участием научно-прак-

тической конференции студентов,

аспирантов, ученых и специали-

стов, посвященной 20-летию соз-

дания кафедры электроэнергетики:

в 2-х томах. Отв. ред. А.Н. Халин.

Тюмень: Тюменский индустриаль-

ный университет, 2019, т. 2. С. 286–

289.

REFERENCES

1. RF Government Executive Order dat-

ed 03.04.2013 no. 511-r “On approval

of the Strategy of power grid devel-

opment”. URL: http://government.ru/

docs/1220/.

2. RF Government Executive Order dat-

ed 03.04.2013 no. 512-r “On approval

of the State program of the Russian

Federation “Energy eﬃ ciency and

power development”. URL: https://

www.garant.ru/products/ipo/prime/

doc/70253012/.

3. Federal State Statistics Service: of-

ﬁ cial site. Moscow. URL: https://ros-

stat.gov.ru/enterprise_industrial.

4. World Bank Group. URL: http://data.

worldbank.org/indicator/EG.ELC.

LOSS.ZS.

5. Vorotnitskiy V.E. Energy saving and

energy eﬃ ciency improvement in elec-

trical networks. Moscow, Heat power

engineer, 2016. 336 p. (In Russian)

6. Buzdko I.A., Vaskhnil N.A., Levin

M.S. Special aspects of optimization

tasks in power industry and methods

of their solution // Electricity, 1981, no.

3, pp. 1–7. (In Russian)

7. Kostin V.N. Optimization tasks of

power industry: study guide. Saint-

Petersburg, SZTU [North-West Cus-

toms], 2003. 120 p. (In Russian)

8. Dale V.A., Krishan Z.P., Paegle O.G.

Mathematic models of power grid de-

velopment optimization // Electricity,

1987, no. 9, pp. 1–6. (In Russian)

9. Shnell’ R.V., Kartavtsev V.V. Optimi-

zation of main transmission parame-

ters // Electricity, 1982, no. 4, pp. 22–

25. (In Russian)

10. Reshetov S.A. Optimization of electri-

cal networks at the set voltage loss //

Electricity, 1982, no. 6, pp. 17–21. (In

Russian)

11. Latypov I.S., Sushkov V.V., Khmara

G.A. Development of generalized ap-

proach to selecting the energy-eﬃ –

cient form of a non-insulated stranded

wire of a 6-35 kV overhead transmis-

sion line //

Promyshlennaya energeti-

[Industrial power], 2020, no. 1, pp.

2–11. (In Russian)

12. Palau I.A.G., Ramirez S.M., Balaba-

niv M.S. and others. Multifunctional

optimization with reactive power

compensation // Tomsk Polytechnic

University review. Geo resource en-

gineering, 2018, vol. 329, no. 12,

pp. 94–103. (In Russian)

13. Chmutov A.P. Optimization of the

voltage mode in distribution networks

by linear inequality theory means //

Electric power stations, 1991, no. 3,

pp. 62–66. (In Russian)

14. Liu Y., Liu S., Niu Z. Distributed Op-

timization for Active Distribution Net-

work Considering the Balance of

Multi-Stakeholder. URL: https://www.

mdpi.com/2227-9717/8/8/987.

15. Zheng W. A Fully Distributed Reac-

tive Power Optimization and Control

Method for Active Distribution Net-

works. URL: https://ieeexplore.ieee.

org/document/7042735.

16. Guiding document RD 34.09.254.

Instruction on reducing the process

consumption of electric power by

grids and interconnections for net-

work transmission. Approved by the

Ministry of Energy of the USSR on

31.03.1986. Moscow, VNIIE [All-

Union Electric Power Research Insti-

tute], 1986. 44 p. (In Russian)

17. Vacuum recloser of series RVA/TEL.

TSHAG 674153.101 TI. Technical

information. URL: http://tavrida-ua.

com/products/vacuumrecloser.html.

18. Bulatov B.G., Tarasenko V.V. Algo-

rithms of intelligent distribution net-

work mode control // South Ural State

University review. Power engineer-

ing, 2012, no. 37(296), pp. 18–22. (In

Russian)

19. Bulatov B.G., Tarasenko V.V. Algo-

rithms of optimal reconﬁ guration of

a distribution network // South Ural

State University review. Power engi-

neering, 2013, vol. 13, no. 2, pp. 14–

18. (In Russian)

20. Vai V., Suk S., Rathana R., Chhlonh C.

[at al]. Optimal Reconﬁ guration in

Distribution Systems with Distrib-

uted Generations Based on Modi-

ﬁ ed Sequential Switch Opening and

Exchange. URL: https://www.mdpi.

com/2076-3417/11/5/2146.

21.Order of the Ministry of Energy of

Russia dated 08.02.2019 no. 81 “On

approval of requirements to the over-

load capacity of transformers and

autotransformers installed in electri-

cal facilities, its maintenance and

on amendments to Grid Code of the

Russian Federation approved by the

order of the Ministry of Energy of Rus-

sia dated June, 19, 2003, no. 229».

URL: https://www.garant.ru/products/

ipo/prime/doc/72109886/.

22. Land A.H., Doig A.G. An automatic

method of solving discrete program-

ming problems. Econometrica, 1960,

no. 3, pp. 497-520.

23. Rokhlov V.A. A PC program: deter-

mination of optimal (from the point

of loss minimization) normal break

points in a 6-10 kV distribution net-

work. А.с. 2021619480 RF. Reg-

istered on 16.04.21; published on

10.07.21.

24. Logunov A.V., Rokhlov V.A. Perspec-

tives of using reclosers in distribution

networks / Proc. of the National with

international participation research-

to-practice conference of students,

Ph.D. students and specialists dedi-

cated to 20-year anniversary of the

power department establishment: in

2 volumes. Editor in chief Khalin A.N.

Tyumen, Tyumen Industrial Universi-

ty, 2019, vol. 2, pp. 286–289. (In Rus-

sian)

ЭНЕРГО-

ЭФФЕКТИВНОСТЬ

Оригинал статьи: Способ снижения потерь электроэнергии в распределительных сетях с двусторонним питанием

Ключевые слова: распределительные сети, реклоузер, потери электроэнергии, потери мощности

Читать онлайн

В статье рассматривается способ снижения потерь в городских и сельских распределительных сетях электроснабжения, выполненных воздушными линиями электропередачи с двусторонним питанием, оборудованными реклоузерами. Предложена математическая модель, методика и алгоритм определения оптимальных с точки зрения минимизации потерь мест нормальных разрывов, осуществляемых реклоузерами.