Оригинал статьи: Разрывное усилие проводов воздушных линий электропередачи
Значение стандартного разрывного усилия многопроволочных проводов по ГОСТ 839-2019 «Провода неизолированные для воздушных линий электропередачи. Технические условия» не соответствуют результатам испытаний проводов на разрыв. В статье дано обоснование снижения фактического разрывного усилия многопроволочного провода по отношению к сумме разрывных усилий составляющих его проволок. Предложена расчетная схема и соответствующие ей формулы. По мнению автора, изложенная в статье методика расчета разрывного усилия подходит для любых свитых из проволоки изделий и конструкций, включая стальные грозозащитные тросы воздушных линий и несущие канаты контактной сети транспорта на электрической тяге.
Мищенко В.В., главный инженер проекта отдела электротехнического оборудования АО «Ленгидропроект»
Разрывное усилие отечественных медных, алюминиевых и сталеалюминевых проводов согласно ГОСТ 839-2019 [1] определяют по обобщенной формуле:

где Pi — фактическое значение разрывного усилия одной медной или алюминиевой проволоки либо усилия одной стальной проволоки при растяжении на 1% (для проволок стального сердечника сталеалюминиевых проводов); n — число проволок в проводе.
Первые экспериментальные исследования многопроволочных проводов показали, что «сопротивление разрыву многопроволочного провода всегда меньше суммы сопротивлений отдельных его проволок» [2]. Этот вывод повторяется авторами [3, 4], а в более поздних работах [5, 6] для проволок стальных сердечников сталеалюминиевых проводов вместо разрывного усилия по временному сопротивлению предлагается использовать усилие при 1%-ном растяжении, которое составляет 80–90% временного сопротивления стальных проволок, что и нашло отражение в [1]. Также в [5] предложены аналогичные (1) формулы для расчета разрывных усилий многопроволочных проводов с эмпирическими коэффициентами, понижающими разрывные усилия отдельных проволок. Результаты испытаний [2] и оценки авторов [3–6] включены в таблицу 1.
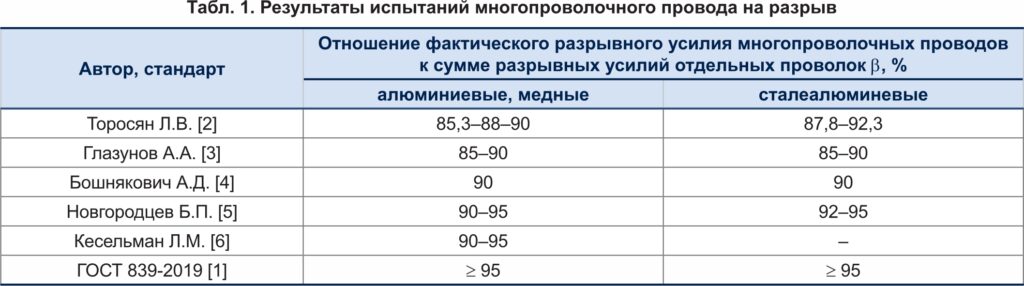
В ГОСТ 839-2019 отмечено, что значение разрывного усилия «при испытании проволок из скрученного провода» должно быть не менее 95% соответствующего стандартного значения. Что подтверждает факт уменьшения разрывного усилия многопроволочного провода по отношению к указанному в [1] стандартному значению, рассчитанному в соответствии с обобщенной формулой (1).
Расхождение между фактическим разрывным усилием многопроволочных проводов и расчетным значением по ГОСТ 839-2019 связано с методом расчета, который не учитывает положение проволоки в проводе. Формула (1) соответствует расчетной модели «нескрученного провода» — пучок прямолинейных параллельно расположенных проволок.
КОНСТРУКЦИЯ МНОГОПРОВОЛОЧНОГО ПРОВОДА
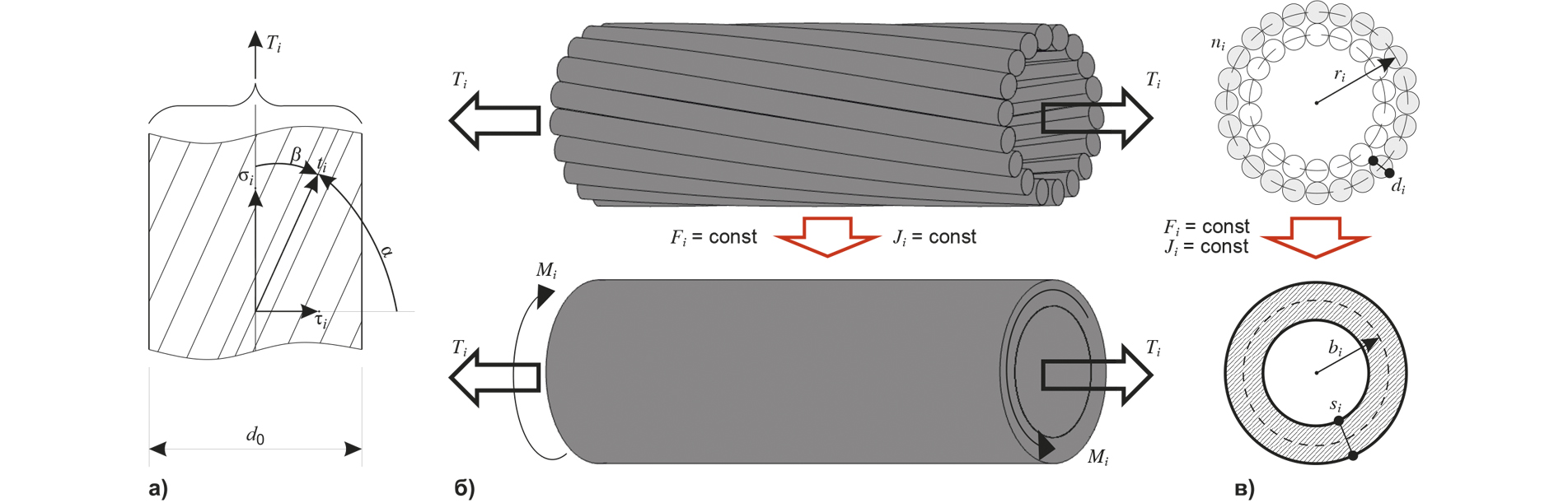
В зависимости от сечения провод имеет несколько слоев проволок, именуемых повивами. Проволоки каждого повива, кроме центральной, после скрутки приобретают винтообразную форму (рисунок 1). Винтообразная форма проволоки приводит к изменению ее напряженного состояния по сравнению с «нескрученным проводом», состоящим из прямолинейных проволок.

Рис. 1. Конструкция провода с тремя проволочными повивами (соседние повивы имеют противоположное направление скрутки) 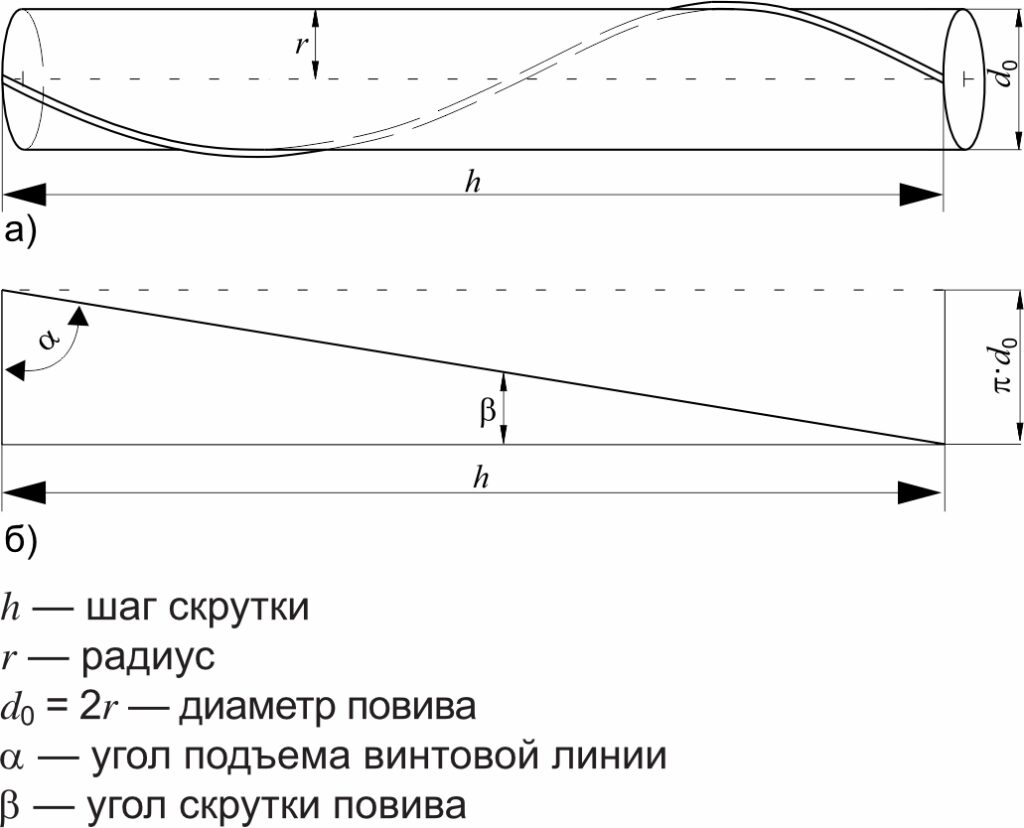
Рис. 2. Положение проволоки в проводе: a) винтовая линия в повиве; б) развертка винтовой линии на плоскость
Расстояние по оси провода между двумя точками проволоки, находящимися на одной образующей, называется шагом скрутки h (рисунок 2).
Отношение шага скрутки к диаметру повива d0 определяет кратность шагов скрутки m:

Кратность шага скрутки в проводах медных и алюминиевых по ГОСТ 839-2019 составляет 10–20, а в сталеалюминиевых проводах 10–28 [1].
ТЯЖЕНИЕ В ПРОВОДЕ — ПРОДОЛЬНАЯ СОСТАВЛЯЮЩАЯ ФАКТИЧЕСКОГО УСИЛИЯ В ПРОВОЛОКАХ
Рассмотрим отдельную проволоку как «волокно» материала, вдоль которого происходит передача фактического усилия в конструкции провода. Такое представление оправданно и для «нескрученного провода» (пучка прямолинейных проволок), и для реального многопроволочного провода. Продольное усилие T представляет сумму воспринимаемых отдельными повивами усилий Ti, где индекс i означает порядковый номер повива, начиная от центральной проволоки, которую условно можно считать «нулевым» повивом. Так как продольное усилие в проводе передается вдоль «волокон», то фактическое усилие в проволоках многопроволочного провода будет больше растягивающего усилия в проволоках «нескрученного» провода. Замеряемое динамометром во время испытания или при монтаже провода тяжение — это сумма продольных составляющих фактического усилия во всех проволоках провода (рисунок 3а).
Оценим фактическое усилие в проволоках повива с кратностью шага скрутки m. Продольная составляющая тяжения всех проволок повива — Ti, подъема винтовой линии — α. Развернув винтовую линию, определяющую положение проволоки в повиве, на плоскость (рисунок 2б), можно с учетом (2) составить простое геометрическое соотношение:
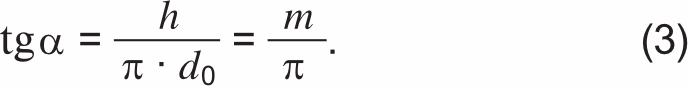
Пусть продольной составляющей тяжения в проволоках i-го повива соответствует напряжение i, тогда с учетом (3) фактическому «тяжению» в i-м повиве, которое действует вдоль оси проволок (рисунок 3а), соответствует напряжение ti:
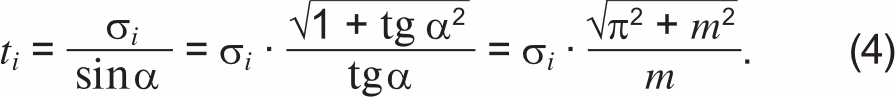
При испытании одиночной проволоки на растяжение предельное состояние достигается при напряжении [σ]. При испытании конструкции многопроволочных проводов на растяжение условное «разрушение» проволок происходит при аналогичном напряжении, то есть tlim = [σ]. Тогда можно с использованием (4) оценить относительное уменьшение предельного σlim, измеряемого при испытании провода в целом, по отношению к расчетному напряжению, соответствующему разрывному усилию по формуле (1):
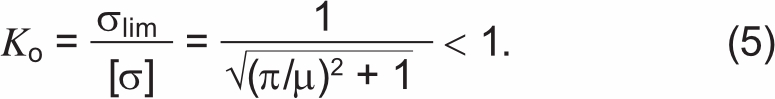
Значение коэффициента Kо, отражающего снижение разрывного усилия многопроволочного повива в зависимости от кратности шага скрутки m, представлено на рисунке 4. Даже при минимально допустимых по [1] значениях кратности шагов скрутки разрывное усилие повива оказывается больше 95% разрывного усилия провода по формуле (1), что не соответствует значениям из [2–6], представленным в таблице 1.
РАСЧЕТНАЯ СХЕМА ПОВИВА МНОГОПРОВОЛОЧНОГО ПРОВОДА
Отдельный i-й повив многопроволочного провода состоит из ni проволок диаметром di. Радиус повива ri — расстояние от центра провода до окружности, на которой расположены центры проволок данного повива. Площадь отдельного повива Fi и его полярный момент Ji относительно оси провода можно найти по известным формулам:
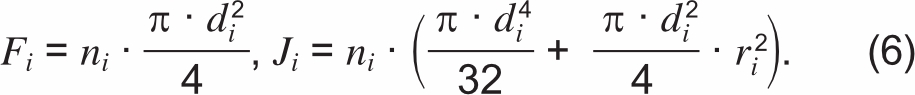
Для определения эквивалентных напряжений с целью применения критериев пластичности и разрушения [7] заменим реальный повив на «трубку» из того же материала. Потребуем, чтобы площадь поперечного сечения и полярный момента «трубки» были равны аналогичным характеристикам исходного повива. При этом в дополнение к продольному осевому усилию Ti на торцах «трубки» появятся противоположно направленные крутящие моменты Mi, которые учитывают особенности реальной конструкции провода: наличие поперечной составляющей τi фактического напряжения в проволоках повива (рисунки 3а и 3б).
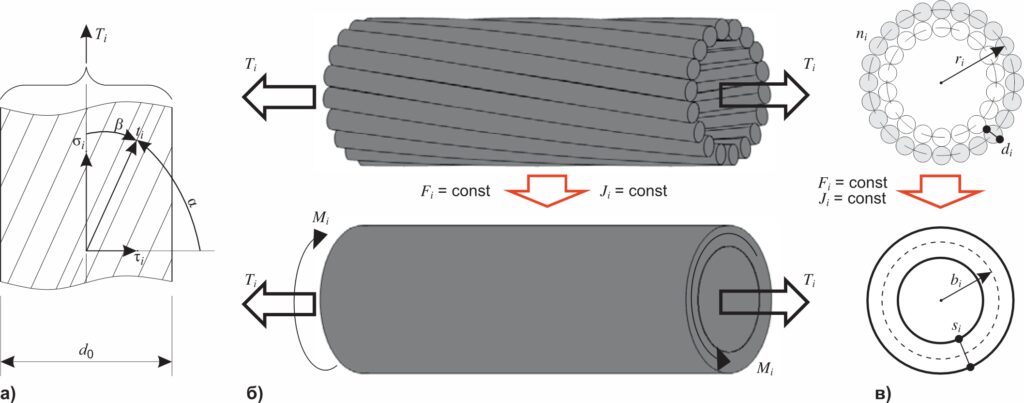
Используя найденные по (6) значения Fi и Ji, можно определить геометрические характеристики расчетного сечения «трубки»:
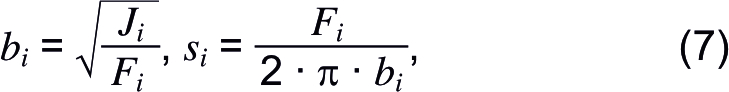
где bi — средний радиус; si — толщина расчетной «трубки» (рисунок 3в).
Следует обратить внимание, что моменты инерции относительно центральных осей «трубки», вычисленные с использованием ее расчетных геометрических характеристики по (7), совпадают с аналогичными значениями реального повива. Таким образом, предлагаемую расчетную схему повива в виде «трубки» также возможно применять при исследовании поведения многопроволочного провода с учетом его изгибной жесткости. При этом провод рассматривается как совокупность соосных «трубок» с радиусами и толщинами по (7), соответствующих конструкции составляющих провод повивов.
ЭКВИВАЛЕНТНЫЕ НАПРЯЖЕНИЯ И ГИПОТЕЗЫ ПРОЧНОСТИ
В сечении «трубки» действуют продольное усилие Ti и крутящий момент Mi, который с учетом (3) и (4) равен:
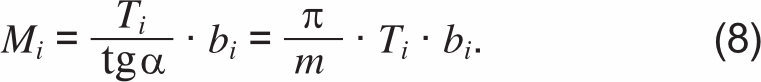
Примем касательные напряжения по толщине «трубки» равными касательному напряжению по среднему радиусу расчетного сечения. Тогда с учетом (7) и (8) получим соотношение, связывающее касательные и нормальные напряжения:
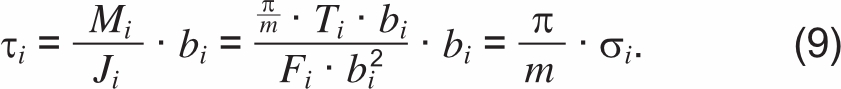
Для принятой расчетной схемы нормальные напряжения в радиальном направлении отсутствуют. Таким образом, материал «трубки» находится в плоском напряженном состоянии. Поэтому для оценки перехода материала «трубки» в предельное состояние возможно использовать формулы эквивалентных напряжений, упрощенные для плосконапряженного состояния [7].
Третья гипотеза прочности или гипотеза наибольших касательных напряжений предполагает, что причиной наступления предельного напряженного состояния в материале являются наибольшие касательные напряжения. Условие прочности запишем в виде отношения предельного напряжения для простого растяжения [σ] к эквивалентному напряжению σIII, соответствующего третьей гипотезе прочности для плосконапряженного состояния. С учетом (9) получим:
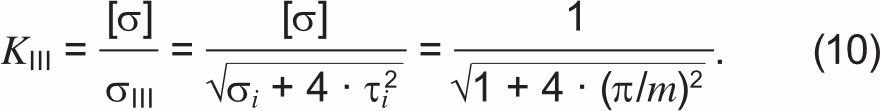
При выводе формулы (10) принято, что предельное состояние расчетной «трубки» (соответствует фактическому разрывному усилию многопроволочного провода) наступает при значении нормального напряжения, равного предельному для простого растяжения [σ], что аналогично выводу формулы (5). Таким образом, (10) представляет отношение фактического разрывного усилия проволок повива к теоретическому, полученному по формуле (1).
Четвертая гипотеза прочности или гипотеза потенциальной энергии формоизменения предполагает, что причиной наступления предельного напряженного состояния в материале является достижение удельной потенциальной энергией формоизменения своей критической величины. Запишем данное условие аналогичным образом: в виде отношения предельного напряжения для простого растяжения [σ] к эквивалентному напряжению σIV, соответствующего разрывному усилию по формуле (1) при четвертой гипотезе прочности для плосконапряженного состояния:
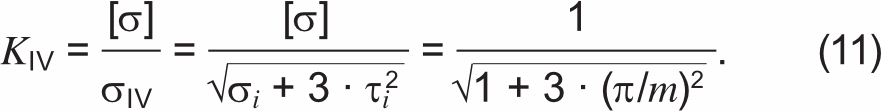
На рисунке 4 представлены графики отношений KIII и KIV в зависимости от кратности шага скрутки m.
Значения кратности шага скрутки приняты в допускаемых по [1] пределах: 10 ≤ m ≤ 28. На рисунке 4 также даны зависимость Kо и ордината 0.95, соответствующая допускаемому «ослаблению» разрывного усилия по [1].
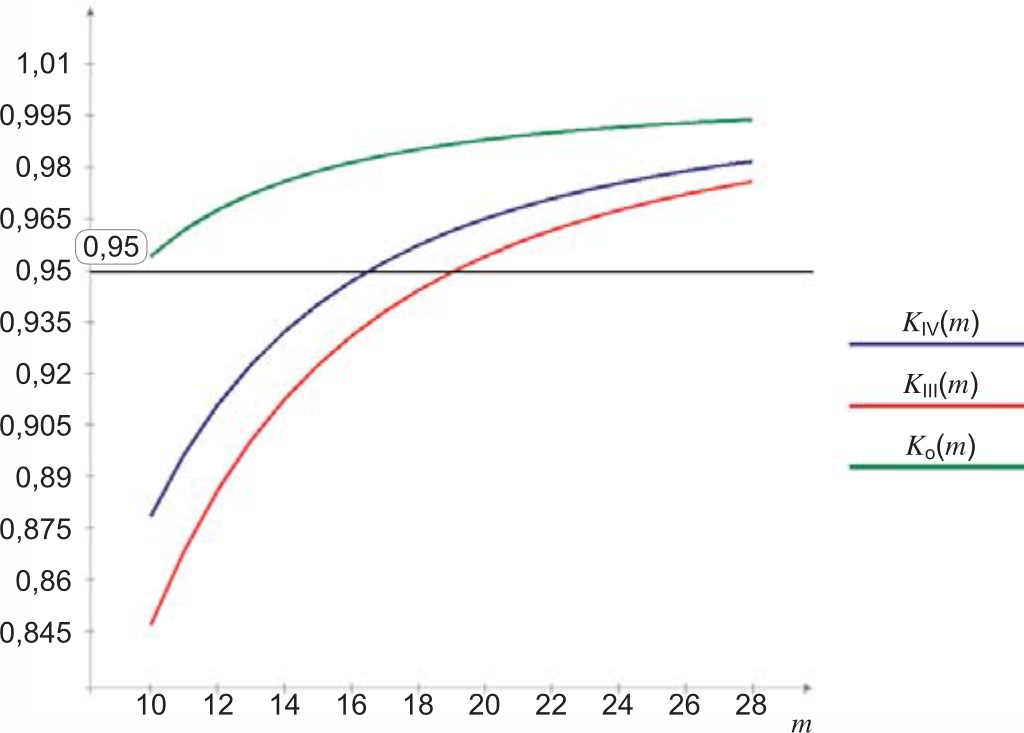
Из графиков на рисунке 4 видно, что при увеличении кратности шага скрутки значение разрывного усилия повива приближается к теоретическому значению по формуле (1). При увеличении параметра m за допускаемые [1] пределы (m > 28) графики асимптотически стремятся к ординате, равной 1. Для «нескрученного провода» или «нулевого повива» (центральная проволока реального провода) кратность шага скрутки m = ∞, а расчетные значения по формулам (5), (10) и (11) становятся равными 1.
ФОРМУЛА ДЛЯ РАСЧЕТА РАЗРЫВНОГО УСИЛИЯ МНОГОПРОВОЛОЧНОГО ПРОВОДА
Предлагается вместо (1) для расчета разрывного усилия многопроволочных проводов по ГОСТ 839-2019 следующая формула:
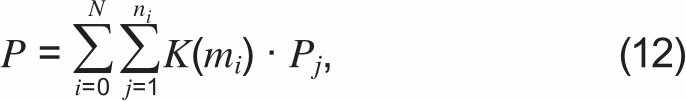
где N — количество повивов в проводе; ni — количество проволок в i-м повиве; K(mi) — коэффициент, учитывающий снижение разрывного усилия проволок i-го повива, скрученного с кратностью шага mi; Pj — фактическое значение разрывного усилия одной медной или алюминиевой проволоки либо усилия одной стальной проволоки при растяжении на 1% (для проволок стального сердечника сталеалюминиевых проводов). Для расчета значения коэффициента K(mi) предлагается использовать выражения (10) или (11), зависящие только от кратности шагов скрутки mi. Центральная нескрученная проволока провода рассматривается как «нулевой» повив, для которого коэффициент K0 равен 1.
Сравним разрывные усилия многопроволочных проводов, полученные в результате натурных испытаний [2], с расчетными значениями, полученными по предлагаемой формуле (12).
В статье Торосяна [2] представлены необходимые данные по конструкции испытанных многопроволочных проводов за исключением шага hi или кратности шага скрутки mi проволок i-го повива. Кратность шага скрутки mi принималась по ГОСТ 839-2019 [1]. Расчет коэффициентов K(mi) выполнялся по формуле (10) и (11) для трех случаев кратности скрутки:
- минимально допустимые значения m (графа βmin в таблице 2);
- максимально допустимые значения m (графа βmax в таблице 2);
- средние значения из диапазона допустимых значений m (графа βmed в таблице 2).
В таблице 2 результаты расчетов представлены значением β (в%), которое есть отношение разрывного усилия провода к суммарному разрывному усилию всех проволок.
Примечания:
1 В [2] имеет место несоответствие между маркой испытанного провода СА-228 и сечением алюминиевой части (фактическое сечение алюминиевой части провода СА-228 составляет 367 мм2 вместо ожидаемых 228 мм2).
2 В [2] указано, что «последние образцы провода СА-228 отличались от предыдущего образца шагом свивки»: диаграммы растяжения в статье [2] представлены для шага свивки 270 и 290 мм. Эти же образцы испытаны на разрыв, но в [2] не указано, какое разрывное усилие соответствует тому или иному шагу свивки. Можно предположить, что меньшее значение разрывного усилия соответствует меньшему шагу свивки. Косвенно это подтверждает один из выводов Торосяна: «С увеличением шага свивки повышается значение модуля упругости, так как провод при этом стремится вести себя как пучок параллельных проволок. К сожалению, не имея большого количества образцов провода с различными шагами свивки, не представляется возможным эту зависимость выразить каким-либо количественным соотношением».
3 Значение в числителе получено по формуле (10), в знаменателе — по формуле (11).
ВЫВОДЫ
1. Фактическое разрывное усилие многопроволочных проводов меньше стандартного разрывного усилия по ГОСТ 839-2019, определяемого как сумма разрывных усилий отдельных проволок по формуле (1). Расчет разрывного усилия по ГОСТ 839-2019 не учитывает влияние конструкции провода: винтообразной формы отдельных проволок в скрученных повивах провода.
2. Геометрия скрученных проволок приводит к появлению неучтенной в формуле (1) поперечной составляющей фактического тяжения в проволоках провода. Измеряемое при испытаниях или при монтаже провода тяжение — продольная составляющая фактического тяжения в проволоках провода.
3. Предложена расчетная схема отдельного скрученного повива многопроволочного провода в виде «трубки» с аналогичными геометрическими характеристиками сечения: площадью, центральными и полярным моментом инерции. Средний радиус и толщина «трубки» с расчетным сечением, эквивалентным реальному повиву, можно определить по формуле (7).
4. На основании предложенной расчетной схемы найдены формулы для определения коэффициента снижения разрывного усилия повива в зависимости от фактического шага или кратности шага скрутки: для гипотезы наибольших касательных напряжений — формула (10), для гипотезы потенциальной энергии формоизменения — формула (11).
5. Предложена формула (12) для расчета разрывного усилия многопроволочных проводов. Согласно (12), относительное снижение разрывного усилия зависит только от конструкции провода: количества повивов, площади сечения проволок и кратности шага скрутки каждого повива. Из формул (10) и (11) следует, что физико-механические свойства материала проволок не влияют на коэффициент снижения разрывного усилия многопроволочного провода. ![]()
ЛИТЕРАТУРА
- ГОСТ 839-2019. Провода неизолированные для воздушных линий электропередачи. Технические условия. URL: https://docs.cntd.ru/document/1200169966.
- Торосян Л.В. Исследование механических свойств проводов // Труды Всесоюзной Электротехнической Ассоциации, 1934, № 11. С. 1–9.
- Глазунов А.А. Основы механической части воздушных линий электропередачи. В 2-х томах: т. 1. М.-Л.: Госэнергоиздат, 1956. 192 с.
- Бошнякович А.Д. Механический расчет проводов и тросов линий электропередачи. М.-Л.: Госэнергоиздат, 1962. 254 с.
- Крюков К.П., Новгородцев Б.П. Конструкции и механический расчет линий электропередачи. Л.: Энергия, 1979. 312 с.
- Кесельман Л.М. Основы механики воздушных линий электропередачи. М.: Энергоатомиздат, 1992. 352 с.
- Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. М.: Изд-во МГТУ им. Н.Э. Баумана, 1999. 592 с.