94
Разработка модели
синхронного генератора
для анализа витковых
замыканий в обмотке
статора
УДК
621.313.333
Глазырин
Г
.
В
.,
к
.
т
.
н
.,
доцент
кафедры
ЭС
НГТУ
Митрофанов
Н
.
А
.,
аспирант
кафедры
ЭС
НГТУ
Ключевые
слова
:
витковые
короткие
за
-
мыкания
, c
инхронная
машина
,
переходной
процесс
,
электроэнер
-
гетическая
система
,
дифференциальные
уравнения
,
численный
метод
Keywords:
inter-winding fault,
synchronous machine,
transient process, electric
power system, differential
equations, numerical
method
Рассматриваются
переходные
процессы
в
автономной
энерго
-
системе
,
состоящей
из
синхронного
генератора
,
повышающего
трансформатора
и
активно
-
индуктивной
нагрузки
.
Предложен
метод
численного
моделирования
переходных
процессов
син
-
хронной
машины
с
возможностью
учета
несимметрии
обмот
-
ки
статора
,
появление
которой
возможно
при
повреждении
синхронной
машины
,
в
частности
,
при
межвитковых
коротких
замыканиях
в
обмотке
статора
.
Метод
основан
на
непосред
-
ственном
решении
дифференциальных
уравнений
равновесия
э
.
д
.
с
.
и
падений
напряжений
в
обмотках
в
фазных
координатах
совместно
с
уравнением
движения
ротора
.
При
этом
контур
каждой
фазной
обмотки
статора
описывается
отдельным
урав
-
нением
,
и
могут
быть
учтены
отличающиеся
параметры
фаз
.
Выполнен
анализ
чувствительности
релейной
защиты
гене
-
ратора
к
межвитковым
коротким
замыканиям
на
примере
результатов
расчета
в
предложенной
математической
модели
переходных
процессов
в
генераторе
с
нарушением
симметрии
обмотки
статора
.
В
результате
исследований
выявлено
,
что
работа
синхронной
машины
при
повреждении
обмотки
статора
,
сопровождающимся
малой
долей
замкнувшихся
витков
(3–15%
от
общего
количества
),
с
большой
вероятностью
останется
вне
зоны
действия
защит
генератора
.
р
е
л
е
й
н
а
я
з
а
щ
и
та
и
а
в
т
о
м
а
т
и
к
а
релейная защит
а и автома
тика
ВВЕДЕНИЕ
Одним
из
самых
значимых
и
сложных
объектов
в
электроэнергетике
,
которому
всегда
уделяется
при
-
стальное
внимание
при
его
защите
и
диагностике
,
предотвращающей
ненормальные
и
аварийные
режи
-
мы
работы
,
является
синхронный
генератор
.
К
релей
-
ной
защите
генератора
,
ввиду
сложности
переходных
процессов
,
проходящих
в
нем
,
предъявляются
осо
-
бые
требования
по
надежности
и
чувствительности
.
Но
далеко
не
все
отклонения
от
режимных
пара
-
метров
возможно
выявить
простыми
,
наглядными
алгоритмами
и
точной
измерительной
системой
за
-
щиты
.
Некоторые
параметры
можно
получить
только
косвенными
методами
измерения
.
К
одному
из
таких
режимов
работы
можно
отнести
несимметрию
фазных
обмоток
статора
,
вызванную
наличием
витковых
замыканий
в
одной
из
них
.
Вит
-
ковые
замыкания
в
обмотке
статора
генератора
не
сопровождаются
значительными
отклонениями
пара
-
метров
,
регистрируемых
релейной
защитой
.
По
этой
причине
стандартный
подход
к
решению
данной
проблемы
не
приносит
желаемого
результата
,

95
то
есть
защита
не
обладает
требу
-
емой
чувствительностью
к
такому
виду
повреждений
.
Но
пренебре
-
жение
таким
режимом
работы
ге
-
нератора
при
отсутствии
ранней
диагностики
данного
повреждения
может
в
значительной
степени
усу
-
губить
его
последствия
.
Речь
идет
о
возможном
развитии
аварии
и
переходе
межвитковых
замыка
-
ний
в
замыкания
на
корпус
маши
-
ны
,
междуфазных
КЗ
.
В
таких
слу
-
чаях
ущерб
от
аварии
возрастает
в
десятки
раз
и
,
что
более
важно
,
сопровождается
несчастными
слу
-
чаями
на
производстве
.
Для
защиты
от
витковых
за
-
мыканий
на
генераторах
большой
мощности
применяют
специаль
-
ную
поперечную
дифференциаль
-
ную
защиту
.
Принцип
действия
ее
основан
на
сравнении
геометри
-
ческой
суммы
токов
в
параллель
-
ных
ветвях
фаз
обмотки
статора
генератора
.
В
нормальном
режиме
и
при
внешнем
коротком
замыка
-
нии
геометрическая
сумма
токов
каждой
группы
параллельных
вет
-
вей
фаз
,
соединенных
в
звезду
,
равна
нулю
и
в
защиту
попадает
только
ток
небаланса
.
Отсюда
следует
первый
недостаток
защи
-
ты
—
необходимость
отстройки
от
тока
небаланса
;
в
результате
ток
срабатывания
защиты
принимает
-
ся
на
уровне
(0,2÷0,3) ·
I
ном
.
Иными
словами
,
защита
имеет
«
мертвую
зону
»
и
при
малой
доле
замкнув
-
шихся
витков
не
будет
обладать
достаточной
чувствительностью
для
срабатывания
.
Второй
недо
-
статок
описываемой
защиты
кроет
-
ся
в
принципе
ее
работы
,
а
именно
в
невозможности
ее
использова
-
ния
в
генераторах
,
обмотка
стато
-
ра
которых
не
расщеплена
.
Таким
образом
поперечная
дифферен
-
циальная
защита
применяется
лишь
в
части
синхронных
машин
,
в
то
время
как
значительное
число
генераторов
остается
вовсе
без
за
-
щиты
от
витковых
замыканий
.
Поэтому
ранняя
диагностика
и
выявление
витковых
замыканий
в
синхронном
генераторе
является
весьма
актуальной
задачей
,
кото
-
рой
посвящается
настоящее
ис
-
следование
.
Аналитическое
исследование
электромагнитных
и
электромеха
-
нических
переходных
процессов
в
синхронной
машине
с
учетом
всех
влияющих
факторов
является
весьма
сложной
задачей
.
В
связи
с
чем
для
упрощения
расчета
при
-
ходится
делать
ряд
допущений
,
которые
вносят
некоторые
погреш
-
ности
в
оценку
рассматриваемых
параметров
синхронной
машины
.
К
основным
допущениям
,
приме
-
няемым
в
практических
методах
расчета
,
можно
отнести
следую
-
щие
[1]:
–
магнитная
система
машины
не
насыщена
,
в
результате
чего
ин
-
дуктивности
машины
не
зави
-
сят
от
намагничивающей
силы
;
–
вместо
действительных
кри
-
вых
распределения
магнитной
индукции
в
воздушном
зазоре
по
расточке
статора
учитыва
-
ются
только
их
составляющие
первой
гармоники
;
–
в
магнитной
системе
машины
отсутствуют
какие
-
либо
потери
.
Существующие
программные
пакеты
моделирования
пере
-
ходных
процессов
в
электро
-
энергетических
системах
,
такие
как
MATLAB Simulink [2], PSCAD,
Mustang,
используют
для
описания
электромагнитных
процессов
син
-
хронной
машины
уравнения
Пар
-
ка
-
Горева
[1],
которые
записыва
-
ются
в
неподвижной
относительно
ротора
системе
координат
и
пред
-
полагают
полную
симметрию
фаз
-
ных
обмоток
статора
.
Очевидно
,
Рис
. 1.
Схема
подключения
нагрузки
a
b
c
i
a.2
i
b.2
i
c.2
R
a.ng2
R
b.ng2
R
c.ng2
Г
a
b
c
i
a.1
i
ab.1
i
ca.1
i
bc.1
a
b
c
L
ca.T1
R
ca.T1
R
ab.T1
L
ab.T1
L
bc.T1
R
bc.T1
i
b.1
i
c.1
0
R
a.T2
R
b.T2
R
c.T2
L
a.T2
L
b.T2
L
c.T2
L
a.ng2
L
b.ng2
L
c.ng2
M
b
M
a
M
c
что
такой
метод
моделирования
не
может
быть
применен
для
расчета
процессов
в
поврежденной
син
-
хронной
машине
с
отличающими
-
ся
параметрами
фазных
обмоток
.
В
статье
приведен
вывод
си
-
стемы
дифференциальных
урав
-
нений
,
описывающих
переходные
процессы
трехфазной
синхронной
машины
с
учетом
индивидуальных
активных
сопротивлений
и
индук
-
тивностей
обмоток
.
Выполнено
мо
-
делирование
работы
синхронной
машины
при
различных
сценариях
витковых
замыканий
.
После
чего
произведена
оценка
чувствитель
-
ности
к
витковым
замыканиям
стандартных
измерительных
орга
-
нов
защит
,
реагирующих
на
откло
-
нения
по
току
.
МОДЕЛЬ
АВТОНОМНОЙ
СИСТЕМЫ
Наиболее
простая
результирую
-
щая
система
дифференциальных
уравнений
получается
в
случае
подключения
нагрузки
по
схеме
«
звезда
»
с
нулевым
проводом
,
не
имеющим
сопротивления
[3]:
до
-
статочно
выполнить
замену
u
на
L
нг
.
(
di
/
dt
) +
R
нг
.
i
в
уравнении
(1).
Фактически
схемы
выдачи
мощности
электростанций
пред
-
усматривают
работу
генераторов
с
изолированной
нейтралью
(
без
нулевого
провода
).
Как
правило
,
генератор
подключается
к
обмот
-
ке
повышающего
трансформато
-
ра
,
соединенной
в
«
треугольник
».
Для
точного
расчета
переходных
процессов
в
таких
схемах
необхо
-
димо
моделирование
как
генера
-
тора
,
так
и
трансформатора
,
что
рассматривается
в
статье
.
Схема
представлена
на
рисунке
1.
Стоит
отметить
,
что
в
ис
-
следовании
учтены
только
три
взаимные
индуктивности
между
первичными
и
вторичными
обмот
-
№
6 (51) 2018

96
ками
трансформатора
.
Взаимные
индуктивности
между
фазами
приняты
равными
нулю
,
что
со
-
ответствует
группе
однофазных
трансформаторов
.
Рассматривалась
синхронная
машина
с
одним
продольным
и
одним
поперечным
демпферны
-
ми
контурами
,
эффект
вытесне
-
ния
токов
не
учитывался
.
Совер
-
шенствованию
методов
расчета
синхронной
машины
при
учете
ротора
машины
многоконтурными
схемами
активно
занимается
[4].
В
рамках
же
поставленных
в
ис
-
следовании
задач
пренебрежение
не
приведет
к
потере
точности
и
недостоверным
результатам
.
Также
на
данном
этапе
ис
-
следования
не
учитывалось
на
-
сыщение
магнитной
системы
машины
,
ввиду
сложности
полу
-
чаемой
системы
уравнений
,
так
как
в
процессе
следует
учитывать
насыщение
магнитной
системы
повышающего
трансформатора
.
Подробно
вопрос
влияния
насы
-
щения
магнитной
системы
на
ве
-
личину
синхронного
индуктивного
сопротивления
изложен
в
[5].
ИСХОДНЫЕ
УРАВНЕНИЯ
,
ХАРАКТЕРИЗУЮЩИЕ
РАБОТУ
СИСТЕМЫ
Рассмотрим
синхронную
машину
,
имеющую
три
фазных
обмотки
,
контур
возбуждения
,
а
также
одну
продольную
и
одну
поперечную
демпферные
обмотки
.
Обозначим
через
u
(
=
a
,
b
,
c
)
и
u
f
мгновенные
значения
напря
-
жений
на
фазных
обмотках
и
об
-
мотке
возбуждения
соответствен
-
но
;
i
и
i
f
—
мгновенные
значения
токов
;
и
f
—
результирую
-
щие
потокосцепления
обмоток
;
R
и
R
f
—
активные
сопротивле
-
ния
фазных
обмоток
и
обмотки
возбуждения
.
Тогда
дифферен
-
циальные
уравнения
равнове
-
сия
э
.
д
.
с
.
и
падений
напряжений
в
контурах
синхронной
машины
будут
иметь
вид
[3]:
(
, , );
.
f
f
f f
d
u
R i
a b c
dt
d
u
R i
dt
η
η
η η
ψ
η
ψ
⎧
= −
−
=
⎪⎪
⎨
⎪
=
+
⎪⎩
(1)
Кроме
того
,
систему
диффе
-
ренциальных
уравнений
(1)
следу
-
ет
дополнить
уравнениями
равно
-
весия
э
.
д
.
с
.
и
падений
напряжений
в
демпферных
контурах
:
РЕЛЕЙНАЯ ЗАЩИТА
И АВТОМАТИКА
у
у
у
у
у
у
0
;
0
,
d
d
d
q
q
q
d
R i
dt
d
R i
dt
ψ
ψ
⎧
= −
−
⎪⎪
⎨
⎪ = −
−
⎪⎩
(2)
где
yd
и
yq
—
результирующие
потокосцепления
продольной
и
попереч
-
ной
демпферных
обмоток
соответственно
,
R
yd
и
R
yq
—
их
активные
сопро
-
тивления
,
i
yd
и
i
yq
—
мгновенные
значения
токов
в
демпферных
контурах
.
Предлагаемый
метод
расчета
переходных
процессов
основан
на
совместном
решении
уравнений
(1)
и
(2),
дополненных
выражениями
падений
напряжений
на
сопротивлениях
трансформатора
и
нагрузки
.
Такой
подход
делает
возможным
моделирование
синхронной
машины
с
различными
параметрами
фазных
обмоток
за
счет
описания
электро
-
магнитных
процессов
в
каждой
фазе
отдельным
дифференциальным
уравнением
.
ВЫВОД
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
ДЛЯ
ИССЛЕДУЕМОЙ
АВТОНОМНОЙ
СИСТЕМЫ
При
расчете
переходных
процессов
синхронной
машины
,
работающей
на
автономную
активно
-
индуктивную
нагрузку
,
необходимо
определить
уравнения
равновесия
э
.
д
.
с
.
и
падений
напряжений
в
контурах
син
-
хронной
машины
в
блоке
с
повышающим
трансформатором
(1):
(
)
(
)
.2
.2
.1
.1
.1
.1
.1
.1
.1
.2
.1
.1
.2
.2
;
cng
cT
bc
cT
bc
bcT
bcT
bc T
cT
c
bcT
bc
c
c
R
R
di
M
di
u
L
L
M
i
R
i
dt
L
dt
L
σ
∑
∑
⎡
⎤
+
⎢
⎥
=
+
−
−
+
⎢
⎥
⎣
⎦
(
)
(
)
.2
.2
.1
.1
.1
.1
.1
.1
.1
.2
.1
.1
.2
.2
;
bng
bT
ab
bT
ab
abT
abT
ab T
bT
b
abT
ab
b
b
R
R
di
M
di
u
L
L
M
i
R
i
dt
L
dt
L
σ
∑
∑
⎡
⎤
+
⎢
⎥
=
+
−
−
+
⎢
⎥
⎣
⎦
⎧
⎪
⎪
⎪
⎪⎪
⎨
⎪
⎪
⎪
⎪
caT
u
(
)
(
)
.2
.2
.1
.1
.1
.1
.1
.1
.1
.2
.1
.1
.2
.2
,
ang
aT
ca
aT
ca
caT
ca T
aT
a
caT
ca
a
a
R
R
di
M
di
L
L
M
i
R
i
dt
L
dt
L
σ
∑
∑
⎡
⎤
+
⎢
⎥
=
+
−
−
+
⎢
⎥
⎣
⎦
⎩
(3)
где
L
kT
.1
, (
k
=
ab
,
bc
,
ca
) —
собственное
значение
индуктивности
первич
-
ной
обмотки
трансформатора
,
обусловленное
основным
магнитным
по
-
током
и
потоком
рассеяния
соответственно
;
M
T
(
=
a
,
b
,
c
) —
взаимная
индуктивность
обмоток
трансформатора
;
L
.2
=
L
ng
.2
+
L
T
.2
+
L
T
.2
—
суммарное
значение
индуктивностей
на
вторичной
стороне
системы
;
R
ng
.2
—
активное
сопротивление
нагрузки
;
R
kT
.1
,
R
kT
.2
—
активное
со
-
противление
первичной
и
вторичной
обмотки
трансформатора
;
u
kT
.1
—
мгновенные
значения
линейных
напряжений
на
первичной
обмотке
трансформатора
,
ij
=
i
–
j
.
При
расчете
переходных
процессов
синхронной
машины
,
работаю
-
щей
на
автономную
активно
-
индуктивную
нагрузку
,
дифференциаль
-
ные
уравнения
принимают
вид
:
(
)
(
)
(
)
.1
.
.
.
.
.1
.
.
.
.
.1
.
.
.
.
;
;
;
ab
abT
g a
g b
ab
g a ca
g b bc
bc
bcT
g b
g c
bc
g b ab
g c ca
ca
caT
g c
g a
ca
g c bc
g a ab
d
u
R
R
i
R i
R i
dt
d
u
R
R
i
R i
R i
dt
d
u
R
R
i
R i
R i
dt
ψ
ψ
ψ
⎧
⎡
⎤
= −
−
+
−
−
⎪
⎣
⎦
⎪
⎪
⎡
⎤
= −
−
+
−
−
⎨
⎣
⎦
⎪
⎪
⎡
⎤
= −
−
+
−
−
⎪
⎣
⎦
⎩
у
у
у
у
у
у
;
;
,
f
f
f f
d
d
d
q
q
q
d
u
R i
dt
d
R i
dt
d
R i
dt
ψ
ψ
ψ
⎧
=
−
⎪
⎪
⎪
= −
⎨
⎪
⎪
= −
⎪
⎩
(4)
где
R
g
.
(
=
a
,
b
,
c
) —
активное
сопротивление
контура
фазной
обмотки
генератора
.
Для
упрощения
восприятия
условно
примем
замену
переменных
:
L
k
(
k
=
ab
,
bc
,
ca
) —
суммарные
собственные
индуктивности
контуров
;
M
k.e
—
эквивалентные
взаимные
индуктивности
контуров
,
u
k
—
мгновенные
значения
падений
напряжения
на
активных
сопротивлениях
контуров
:

97
2
.1
.1
.1
.2
2
.1
.1
.1
.2
2
.1
.1
.1
.2
2
;
2
;
2
;
bT
ab
a
b
ab
abT
ab T
b
cT
bc
b
c
bc
bcT
bc T
c
aT
ca
c
a
ca
caT
ca T
a
M
L
L
L
M
L
L
L
M
L
L
L
M
L
L
L
M
L
L
L
M
L
L
L
σ
σ
σ
Σ
∑
Σ
∑
Σ
∑
=
+
−
+
+
+
=
+
−
+
+
+
=
+
−
+
+
+
.
.
;
ab e
bc
ab
ca
b
bc e
bc
ca
ab
c
M
M
M
M
L
M
M
M
M
L
=
+
−
−
=
+
−
−
.
;
ca e
ca
ab
bc
a
M
M
M
M
L
=
+
−
−
(
)
(
)
(
)
(
)
(
)
(
)
.2
.2
.1
.2
.
.
.1
.
.
.2
.2
.2
.1
.2
.
.
.1
.
.
.2
.2
.2
.1
.2
.
.
.1
.
.
.2
;
;
bng
bT
ab
bT
b
g a
g b
ab
ab
g a ca
g b bc
b
cng
cT
bc
cT
c
g b
g c
bc
bc
g b ab
g c ca
c
ang
aT
ca
aT
a
g c
g a
ca
ca
g c bc
g a
a
R
R
u
M
i
R
R
R
i
R i
R i
L
R
R
u
M
i
R
R
R
i
R i
R i
L
R
R
u
M
i
R
R
R
i
R i
R
L
∑
∑
∑
∑
∑
∑
+
= −
−
+
+
+
+
+
= −
−
+
+
+
+
+
= −
−
+
+
+
+
.
ab
i
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
⎧
⎪
⎪
⎨
⎪
⎪
⎩
(5)
Коэффициенты
пропорциональности
L
a
,
L
b
,
L
c
,
L
f
,
L
yd
,
L
yq
есть
соб
-
ственные
индуктивности
фазных
обмоток
,
обмотки
возбуждения
,
про
-
дольной
и
поперечной
демпферных
обмоток
соответственно
,
симво
-
лом
M
обозначены
взаимные
индуктивности
обмоток
.
Как
определяются
эти
коэффициенты
,
подробно
раскрыто
в
[6],
и
останавливаться
на
их
рассмотрении
не
имеет
смысла
.
Стоит
лишь
отметить
,
что
большин
-
ство
индуктивностей
,
входящих
в
выражение
(5),
являются
функциями
угла
поворота
ротора
.
Решение
системы
уравнений
(1)
включает
в
себя
определение
про
-
изводной
d
/
dt
от
сложной
функции
,
зависящей
от
токов
в
контурах
и
угла
поворота
ротора
.
Для
этого
к
системе
(2)
применим
следующую
формулу
производной
сложной
функции
:
∑
∂
∂
+
∂
∂
=
m
m
m
m
k
k
dt
di
i
dt
d
dt
d
ψ
γ
γ
ψ
ψ
, (
k
=
ab
,
bc
,
ca
)
и
подставим
полученные
выражения
в
(1).
Так
как
процесс
определения
производных
для
разных
контуров
однотипен
,
рассмотрим
лишь
одно
уравнение
для
контура
«
ab
»
статора
:
(
)
.
.
.
.
f
ab
ab
ab
bc
ca
ab e
ab e
ca e
af
bf
di
d
di
di
di
L
M
M
M
M
dt
dt
dt
dt
dt
ψ
ψ
ω
γ
∂
=
+
+
+
+
−
+
∂
(
)
(
)
у
у
n.
.
d
q
ab
ayd
byd
ayq
byq
ab
ab
di
di
di
M
M
M
M
L
u
dt
dt
dt
∑
+
−
+
−
= −
−
(6)
Уравнения
для
остальных
контуров
могут
быть
получены
тем
же
способом
.
Частную
производную
потокосцепления
по
углу
,
входящую
в
(6),
вы
-
разим
следующим
образом
:
(
)
.
.
.
.
af
bf
ab
ab e
ab e
ca e
ab
bc
ca
f
d M
M
dL
dM
dM
i
i
i
i
d
d
d
d
ψ
γ
γ
γ
γ
γ
−
∂
=
+
+
+
+
∂
(
)
(
)
у
у
.
ayd
byd
ayq
byq
d
q
d M
M
d M
M
i
i
d
d
γ
γ
−
−
+
+
(7)
Выведенные
в
(6)
производные
индуктивностей
по
углу
можно
опре
-
делить
,
зная
исходные
выражения
индуктивностей
,
полученные
в
[6].
В
результате
подстановки
(7)
в
(6)
получим
уравнение
,
связывающее
функции
времени
—
токи
в
обмотках
и
угол
поворота
ротора
—
и
произ
-
водные
этих
функций
.
При
рассмотрении
всех
контуров
синхронной
машины
вместо
од
-
ного
уравнения
(6)
получим
следующую
систему
уравнений
в
матрич
-
ном
виде
:
.
.
.
у
у
.
.
.
у
у
.
.
у
у
у
у
у
у
у
у
у
у
у
у
у
0
0
0
0
ab
ab e
ca e
abf
ab d
ab q
ab
ab e
bc
bc e
bcf
bc d
bc q
bc
ca e
bc e
ca
caf
ca d
ca q
ca
abf
bcf
caf
f
f d
f
ab d
bc d
ca d
f d
d
d
ab q
bc q
ca q
q
L
M
M
M
M
M
di
dt
M
L
M
M
M
M
di
dt
M
M
L
M
M
M
di
dt
M
M
M
L
M
di
dt
M
M
M
M
L
di
dt
M
M
M
L
di
Σ
Σ
Σ
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⋅
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
у
у
у
у
у
у
у
(
)
(
)
(
)
,
(
)
(
)
(
)
ab
ab
bc
bс
ca
сa
f
f f
f
d
d
d
q
q
q
q
u
u
u
R i
u
R i
dt
R i
ψ
γ ω
ψ
γ ω
ψ
γ ω
ψ
γ ω
ψ
γ ω
ψ
γ ω
∑
∑
∑
− ∂
∂
+
⎡
⎤ ⎡
⎤
⎢
⎥ ⎢
⎥
− ∂
∂
+
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
− ∂
∂
+
=
⎢
⎥ ⎢
⎥
− ∂
∂
−
+
⎢
⎥ ⎢
⎥
⎢
⎥ ⎢
⎥
− ∂
∂
−
⎢
⎥ ⎢
⎥
− ∂
∂
−
⎢
⎥ ⎢
⎥
⎣
⎦ ⎣
⎦
(8)
где
M
kf
,
M
yd
,
M
yq
(
k
=
ab
,
bc
,
ca
) —
значения
взаимной
индуктивности
обмотки
возбуждения
,
продоль
-
ной
и
поперечной
демпферных
обмоток
.
Помимо
системы
(8),
необхо
-
димо
определить
значения
токов
во
вторичной
обмотке
трансфор
-
матора
,
для
чего
воспользуемся
системой
уравнений
:
(
)
(
)
(
)
.2
.2
.2
.1
.1
.2
.2
.2
.2
.2
.2
.1
.1
.2
.2
.2
.2
.2
.2
.1
.1
.2
.2
.2
;
;
.
ang
aT
a
aT
ca
a
a
a
bng
bT
b
bT
ab
b
b
b
cng
cT
c
cT
bc
c
c
c
R
R
di
M
di
i
dt
L
dt
L
R
R
di
M
di
i
dt
L
dt
L
R
R
di
M
di
i
dt
L
dt
L
∑
∑
∑
∑
∑
∑
⎧
+
⎪
=
−
⎪
⎪
+
⎪
=
−
⎨
⎪
⎪
+
⎪
=
−
⎪
⎩
Полученная
система
урав
-
нений
(8)
позволяет
определять
производные
токов
в
обмотках
по
известным
значениям
функций
(
токов
,
угла
поворота
ротора
и
ча
-
стоты
).
МОДЕЛИРОВАНИЕ
ПЕРЕХОДНОГО
ПРОЦЕССА
В
СИСТЕМЕ
ПРИ
ВИТКОВЫХ
КОРОТКИХ
ЗАМЫКАНИЯХ
ОБМОТКИ
СТАТОРА
ГЕНЕРАТОРА
Практическими
методами
рас
-
чета
переходных
процессов
синхронной
машины
активно
занимается
С
.
А
.
Харитонов
[7]
(
описание
электромагнитных
пе
-
реходных
процессов
в
системах
генерирования
электрической
энергии
для
автономных
объек
-
тов
).
Предложенная
математиче
-
ская
модель
автономной
энер
-
госистемы
реализована
при
помощи
программного
пакета
MATLAB.
Данная
программа
ши
-
роко
применяется
в
различного
рода
исследованиях
переходных
процессов
в
синхронных
и
асин
-
хронных
машинах
[8–11].
Для
решения
системы
диф
-
ференциальных
уравнений
ис
-
пользована
функция
ode45,
ос
-
нованная
на
одношаговом
явном
методе
Рунге
-
Кутта
4-
го
и
5-
го
порядка
[2].
За
основу
метода
расчета
производных
при
чис
-
ленном
решении
системы
диф
-
ференциальных
уравнений
взят
алгоритм
,
предложенный
в
[6].
Однако
не
всегда
применение
пакета
MATLAB
отвечает
требу
-
емому
быстродействию
.
Для
по
-
№
6 (51) 2018
98
вышения
скорости
вычислений
авторы
[3, 12]
предлагают
мето
-
ды
дополнительной
оптимизации
программного
кода
.
В
качестве
примера
для
срав
-
нения
моделей
выполнены
рас
-
четы
переходных
процессов
генератора
ТВВ
-200-2A
У
3
с
уче
-
том
несимметрии
фазных
обмо
-
ток
статора
и
трансформатора
ТДЦ
-250000/110.
В
рамках
данной
статьи
рас
-
смотрен
только
один
из
возмож
-
ных
случаев
неисправности
—
уменьшенное
число
витков
в
фазной
обмотке
статора
.
Тем
самым
моделируется
витковое
короткое
замыкание
без
учета
появления
дополнительных
ко
-
роткозамкнутых
контуров
.
Отно
-
шение
числа
витков
в
обмотке
к
числу
витков
в
исправном
состо
-
янии
обозначим
k
w
(
=
a
,
b
,
c
).
Взаимные
индуктивности
об
-
мотки
пропорциональны
числу
витков
в
ней
,
а
собственная
ин
-
дуктивность
—
квадрату
числа
витков
.
Подробно
вывод
соответ
-
ствующих
выражений
отражен
в
[6],
поэтому
останавливаться
на
них
не
имеет
смысла
.
Работа
системы
рассматри
-
вается
в
нескольких
режимах
:
витковое
короткое
замыкание
из
нормального
установившегося
режима
под
нагрузкой
;
пуск
по
-
врежденной
синхронной
машины
и
выход
на
установившийся
ре
-
жим
под
нагрузкой
.
Повреждение
происходит
в
об
-
мотке
фазы
«
А
»
генератора
с
ко
-
эффициентами
витковых
замы
-
каний
k
wa
0,9
= 0,9;
k
wa
0,5
= 0,5.
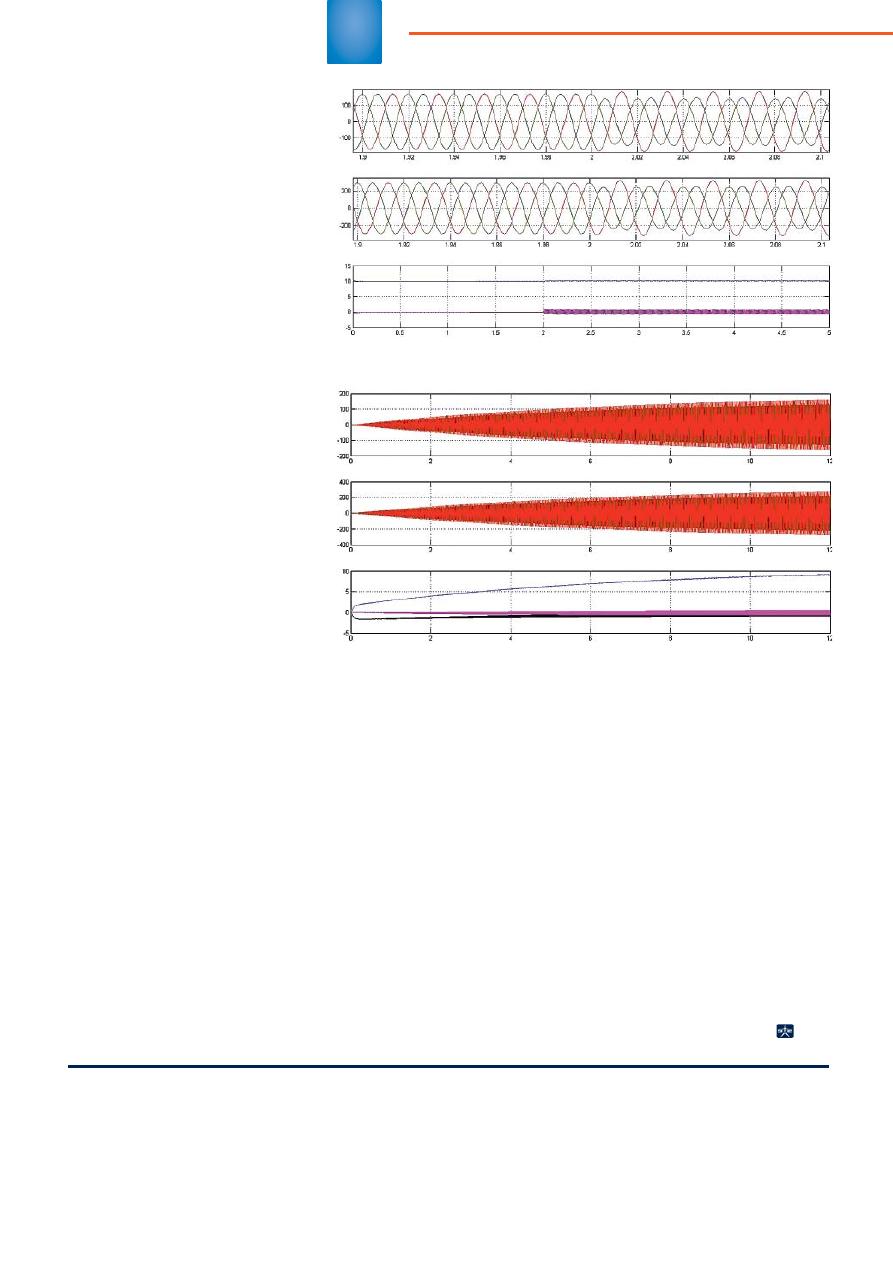
На
рисунке
2
представлен
переход
-
ной
процесс
,
сопровождающийся
возникновением
виткового
корот
-
кого
замыкания
с
коэффициентом
k
wa
0,5
.
После
выполнения
анализа
осциллограмм
переходных
про
-
цессов
,
получено
различие
в
зна
-
чениях
токов
в
здоровой
и
повреж
-
денной
фазе
на
4,5%
при
k
wa
0,9
,
на
23,4%
при
k
wa
0,5
.
Таким
образом
,
можно
сделать
вывод
о
том
,
что
при
малой
доле
замкнувшихся
витков
выявить
повреждение
тра
-
диционными
методами
не
пред
-
ставляется
возможным
.
На
рисунке
3
отображен
пере
-
ходной
процесс
запуска
синхрон
-
ного
генератора
и
выхода
его
на
номинальный
режим
работы
при
наличии
повреждения
в
обмотке
статора
с
коэффициентом
k
wa
0,5
.
Резюмируя
вышеописанные
результаты
,
можно
сказать
,
что
работа
синхронной
машины
при
повреждении
обмотки
статора
,
сопровождающемся
малой
до
-
лей
замкнувшихся
витков
(3–15%
от
обмотки
),
с
большой
вероят
-
ностью
останется
вне
зоны
дей
-
ствия
большей
части
РЗ
генера
-
тора
.
Данного
рода
повреждение
однозначно
не
идентифицируют
-
ся
как
витковое
короткое
замыка
-
ние
,
а
,
следовательно
,
не
будут
вовремя
приняты
соответствую
-
щие
меры
по
аварийному
остано
-
ву
генератора
.
На
основании
предложенной
модели
переходных
процессов
в
синхронной
машине
на
данный
момент
выполняется
разработка
алгоритмов
и
признаков
своевре
-
менного
выявления
витковых
ко
-
ротких
замыканий
с
целью
после
-
дующей
интеграции
в
системы
мониторинга
и
релейной
защиты
синхронного
генератора
.
Рис
. 2.
Переходной
процесс
в
синхронном
генераторе
при
витковом
КЗ
и
k
wa
0,5
Рис
. 3.
Переходной
процесс
запуска
синхронного
генератора
при
витковом
КЗ
и
k
wa
0,5
i
f
,
i
y
,
кА
i
,
А
U
ng
,
кВ
t
, c
t
, c
t
, c
i
f
,
i
y
,
кА
i
,
А
U
ng
,
кВ
t
, c
t
, c
t
, c
Литература
1.
Ульянов
С
.
А
.
Электромагнитные
переходные
про
-
цессы
в
электрических
системах
.
М
.:
Энергия
, 1970.
518
с
.
2.
Моделирование
электротехничес
ких
устройств
в
MAT-
LAB. Sim Power Systems
и
Simulink.
Москва
:
ДМК
Пресс
,
2013. 288
с
.
3.
Глазырин
Г
.
В
.
Моделирование
переходных
процессов
синхронной
машины
с
несимметрией
фазных
обмоток
статора
//
Вестник
МЭИ
, 2017,
№
5.
С
. 34–39.
4.
Сивокобыленко
В
.
Ф
.
Математическое
моделирование
синхронной
машины
с
многоконтурным
ротором
в
фаз
-
ных
координатах
//
Техническая
электродинамика
,
2015,
№
1.
С
. 51–58.
РЕЛЕЙНАЯ ЗАЩИТА
И АВТОМАТИКА

99
5.
Жданов
П
.
С
.
Вопросы
устойчивости
электрических
си
-
стем
.
М
.:
Энергия
, 1979. 456
с
.
6.
Горев
А
.
А
.
Переходные
процессы
синхронной
машины
.
Л
.:
Наука
, 1985. 502
с
.
7.
Харитонов
С
.
А
.
Электромагнитные
переходные
про
-
цессы
в
системах
генерирования
электрической
энер
-
гии
для
автономных
объектов
:
монография
.
Новоси
-
бирск
:
Изд
-
во
НГТУ
, 2011. 536
с
.
8.
Файзиев
М
.
М
.,
Курбонов
Н
.
А
.,
Имамназаров
А
.
Б
.,
Бе
-
кишев
А
.
Э
.
Моделирование
пуска
асинхронных
двига
-
телей
в
МА
TLAB //
Вестник
науки
и
образования
, 2017,
№
3(27).
С
. 42–47.
9.
Субботина
В
.
А
.,
Тюленев
М
.
Е
. Simulink —
модель
для
исследования
пуска
синхронного
двигателя
при
пони
-
женном
напряжении
//
Электротехника
,
информаци
-
онные
технологии
,
системы
управления
, 2014,
№
11.
С
. 102–109.
10.
Федий
К
.
С
.,
Встовский
С
.
А
.,
Полошков
Н
.
Е
.
Моделиро
-
вание
переходных
процессов
в
торцевом
синхронном
генераторе
в
пакете
MATLAB //
Журнал
Сибирского
фе
-
дерального
университета
.
Техника
и
технологии
, 2017,
№
10(5).
С
. 691–698.
11. Demiroren A. and Zeynelgil H.L. Modelling and simulation
of synchronous machine transient analysis using SIMULINK
// International Journal of Electrical Engineering Education,
2002, 39/4, pp. 337–346.
12. Hafnaoui I., Ayari R., Nicolescu G., Beltrame G. A simu-
lation-based model generator for software performance
estimation: SCSC’16 Proceedings of the Summer
Computer Simulation Conference, USA, 2016.
REFERENCES
1. Ulyanov S.A. Electromagnetic transients in electrical sys-
tems. M.: Energy, 1970. 518 p.
2. Chernyih I.V. Modeling of electrical devices in MATLAB.
SimPowerSystems and Simulink. M.: HMC Press, 2008.
288 p.
3. Glazyirin G.V. Simulation of transient processes of a syn-
chronous machine with the asymmetry of phase stator
windings // Newsletter MEI, 2017, No. 5, pp. 34–39.
4. Sivokobyilenko V.F. Mathematical modeling of a synchro-
nous machine with a multi-loop rotor in phase coordinates
// Technical electrodynamics, 2015, No. 1, pp. 51–58.
5. Zhdanov P.S. Questions of the stability of electrical sys-
tems. M.: Energy, 1979. 456 p.
6. Gorev A.A. Transient processes of a synchronous ma-
chine. L.: Science, 1985. 502 p.
7. Haritonov S.A. Processes in Power Generating Systems
for Stand-Alone Units. N.: NSTU, 2011. 536 p.
8. Fayziev M.M., Kurbonov N.A., Imamnazarov A.B., Beki-
shev A.E. Modeling of start-up of asynchronous motors
in
МА
TLAB // Bulletin of Science and Education, 2017,
No. 3(27), pp. 42–47.
9. Subbotina V.A., Tyulenev M.E. Simulink is a model for in-
vestigating the start-up of a synchronous motor under re-
duced voltage // Electrical engineering, information tech-
nology, control systems, 2014, No. 11, pp.102–109.
10. Fediy K.S., Vstovsky S.A., Poloshkov N.E. Simulation of
transients in the face synchronous generator in the MAT-
LAB package // Journal of Siberian Federal University. En-
gineering and technology, 2017, No. 10 (5), pp. 691–698.
11. Demiroren A. and Zeynelgil H.L. Modelling and simulation
of synchronous machine transient analysis using SIMU-
LINK // International Journal of Electrical Engineering Edu-
cation, 2002, 39/4, pp. 337–346.
12. Hafnaoui I., Ayari R., Nicolescu G., Beltrame G. A simula-
tion-based model generator for software performance es-
timation: SCSC’16 Proceedings of the Summer Computer
Simulation Conference, USA, 2016.
Выставочный центр
“ЦАРИЦЫНСКАЯ ЯРМАРКА”
valya@zarexpo.ru
(8442) 26-50-34
3-5
апреля
Волгоград Арена
ЭНЕРГО-VOLGA-2019
межрегиональный форум
ЭНЕРГОСБЕРЕЖЕНИЕ
ЭНЕРГОЭФФЕКТИВНОСТЬ
выставка
Организаторы:
Администрация Волгоградской области,
ВЦ “Царицынская ярмарка”
Генеральный
информационный партнер
№
6 (51) 2018
Оригинал статьи: Разработка модели синхронного генератора для анализа витковых замыканий в обмотке статора
Рассматриваются переходные процессы в автономной энергосистеме, состоящей из синхронного генератора, повышающего трансформатора и активно-индуктивной нагрузки. Предложен метод численного моделирования переходных процессов синхронной машины с возможностью учета несимметрии обмотки статора, появление которой возможно при повреждении синхронной машины, в частности, при межвитковых коротких замыканиях в обмотке статора. Метод основан на непосредственном решении дифференциальных уравнений равновесия э.д.с. и падений напряжений в обмотках в фазных координатах совместно с уравнением движения ротора. При этом контур каждой фазной обмотки статора описывается отдельным уравнением, и могут быть учтены отличающиеся параметры фаз. Выполнен анализ чувствительности релейной защиты генератора к межвитковым коротким замыканиям на примере результатов расчета в предложенной математической модели переходных процессов в генераторе с нарушением симметрии обмотки статора. В результате исследований выявлено, что работа синхронной машины при повреждении обмотки статора, сопровождающимся малой долей замкнувшихся витков (3–15% от общего количества), с большой вероятностью останется все зоны действия защит генератора.