Разработка математической модели дуговой сталеплавильной печи

Page 1

Разработка математической модели
дуговой сталеплавильной печи

УДК 621.365.22

Сорокин

к.т.н., доцент, профессор

кафедры электрических систем

ИГЭУ им. В.И. Ленина

Молчагина

магистрант ИГЭУ им. В.И. Ленина;

специалист службы кадрового

резерва 1-й категории филиала

АО «СО ЕЭС» — ОДУ Центра

Сидоров

магистрант ИГЭУ им. В.И. Ленина;

специалист службы кадрового

резерва 1-й категории филиала

АО «СО ЕЭС» — ОДУ Центра

Электрические

дуговые

сталеплавильные

печи

(

ДСП

)

являются

одним

из

основных

агре

гатов

для

плавки

высококачественных

легированных

сталей

Благодаря

их

ключевым

особенностям

(

быстрому

нагреву

металлов

возможности

поддержания

заданной

темпе

ратуры

химического

состава

)

ДСП

занимают

лидирующие

позиции

сталеплавильной

индустрии

по

всему

миру

Однако

связи

особенностями

технологического

процесса

дуговые

сталеплавильные

печи

являются

потребителем

электроэнергии

оказывающим

крайне

негативное

влияние

на

питающую

сеть

современной

российской

практике

вопросы

связанные

влиянием

работы

ДСП

на

показатели

качества

электроэнергии

обычно

решаются

эмпирическими

методами

не

способными

полной

мере

учесть

все

особенности

процесса

Авторами

статьи

описывается

процесс

разработки

математиче

ской

модели

применение

которой

возможно

как

на

производстве

так

образователь

ном

процессе

Ключевые

слова

дуговые сталеплавильные печи,

дуга, печь, сталь, математическая

модель, ДСП-20, короткая сеть,

печной трансформатор

лектрическая дуговая сталеплавильная печь представляет собой

совокупность электротехнических агрегатов, преобразующих элек-

трическую энергию в тепловую, под воздействием которой про-

исходит расплавление металла. Согласно закону Джоуля-Ленца,

для выделения большого количества тепла необходимо подведение к ших-

те тока большой амплитуды, поэтому внутрь рабочего пространства печи

электроэнергия поставляется по специальным электродам. При работе печи

между электродами и расплавляемым металлом загорается электрическая

дуга. На некоторых стадиях плавления дуга является неустойчивой и может

часто обрываться, либо перекрываться на корпус. В связи с этим еще одним

важным агрегатом ДСП являются приводы электродов, осуществляющие

их перемещение внутри печи. Для обеспечения питания печи токами номи-

нального значения применяется печной трансформатор, осуществляющий

преобразование напряжения с класса распределительного пункта предпри-

ятия до номинала печи. Ключевой особенностью печного трансформатора

является высокое значение напряжения короткого замыкания и возможность

регулирования напряжения под нагрузкой в гораздо более широком диапа-

зоне, нежели позволяют типовые нагрузочные трансформаторы [1]. Все эти

элементы нуждаются в точном и подробном моделировании. Описание каж-

дого из них достойно отдельной статьи, однако в рамках данной публикации

хочется обратить внимание именно на моделирование дуги ДСП.

В современных российских исследованиях при моделировании элек-

трической дуги принято пользоваться уравнением Касси, описывающим

значение ее проводимости [2, 3]:

— = — · — –



где

— проводимость дуги;

— мгновенное значение тока дуги;

— про-

тивоЭДС дуги;



— постоянная времени проводимости дуги.

Применение данного уравнения зарекомендовало себя по сравнению

с устаревшими представлениями нелинейностей в ДСП постоянным сопро-

тивлением или постоянным напряжением и оказывается весьма точным

в случаях, когда важны пиковые значения кривой токов (например, при мо-

делировании дуги в дугогасящих камерах выключателей при отключении

токов короткого замыкания). Однако, говоря про дуговые сталеплавильные

печи, важно понимать, что режим ее работы был уже рассчитан, а основное

влияние на показатели качества электроэнергии оказывают именно момен-

ты прохождения кривой тока через ноль. Именно поэтому в зарубежной ли-

тературе нашло применение расширенное уравнение Майера-Касси [4]:

min

+ (1 –



) · — ·



· — –



· —,

№

3 (54) 2019

Page 2

где

min

— минимальная проводи-

мость дуги;



— коэффициент, учи-

тывающий стадию плавления дуги;

— тепловые потери в печи.

При сравнении становится оче-

видно, что расширенное уравнение

учитывает большее количество вли-

яющих факторов при введении всего

одной новой переменной, являющей-

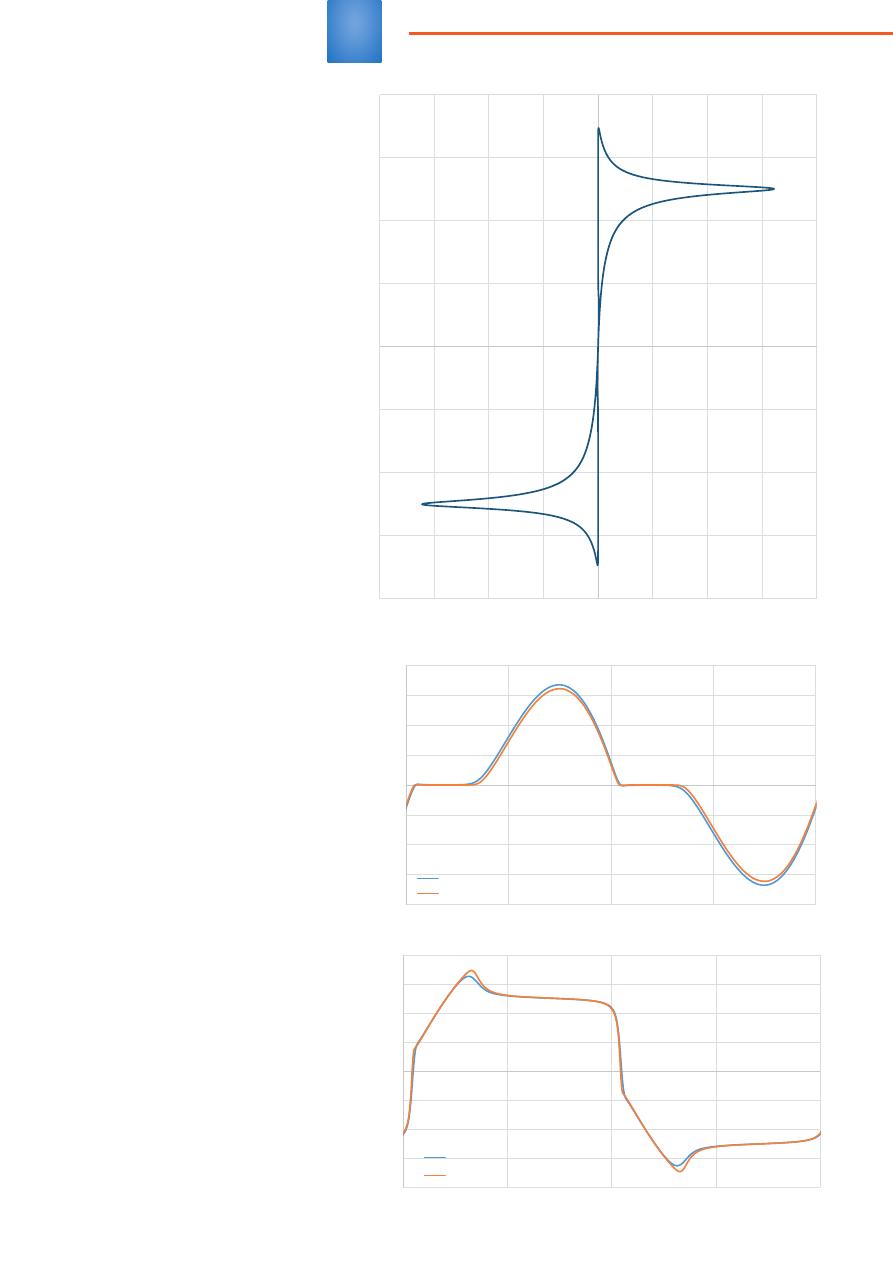
ся паспортной величиной печи. На

рисунке 1 представлена вольтампер-

ная характеристика, полученная при

решении уравнения Майера-Касси.

На рисунках 2 и 3 приведены сравне-

ния кривых токов и напряжений, по-

лученных по различным уравнениям.

Несмотря на то, что на первый

взгляд отличия незначительны, край-

не важными являются значения на

перегибах характеристики, так как

именно при малых значениях токов

велико влияние высших гармоник,

ухудшающих показатели качества

электроэнергии.

Значительные отличия в местах

перегиба характеристики делают ра-

циональным использование именно

модели Майера-Касси для рассмо-

трения влияния ДСП на показатели

качества электроэнергии.

В вопросах, связанных с моде-

лированием реальных устройств,

крайне важным является соблюде-

ние баланса между числом входных

переменных, описывающих модель,

и легкостью получения их значений.

Создание модели, учитывающей все

факторы вплоть до температуры на-

ружного воздуха и атмосферного

давления, возможно в теории, но не

является уместным на практике —

большое количество входных дан-

ных значительно усложняет модель,

а любое неправильно подобранное

значение может полностью иска-

зить результаты расчета. В связи

с этим при создании модели была

цель ограничится теми переменны-

ми, доступ к которым есть на каждом

предприятии, а именно: паспортны-

ми данными печи, печных агрегатов

и параметрами сети. Уравнение Май-

ера-Касси полностью соответствует

этим критериям.

При разработке модели также

важно было оградить пользовате-

ля от «внутренностей» самой мо-

дели, позволяя в первом приближе-

нии ограничиться только заданием

входных данных и исследованием

результатов. Для этих целей идеаль-

но подходит приложение к пакету

Matlab/Simulink. При моделирова-

-400

-300

-200

-100

100

200

300

400

-40000

-30000

-20000

-10000

10000

20000

30000

40000

ду

ги

, В

дуги, А

-40 000

-30 000

-20 000

-10 000

10 000

20 000

30 000

40 000

0,04

0,045

0,05

0,055

0,06

ду

ги

, A

, c

Уравнение Майера-Касси

Уравнение Касси

-400,00

-300,00

-200,00

-100,00

0,00

100,00

200,00

300,00

400,00

0,04

0,045

0,05

0,055

0,06

ду

ги

, В

, c

Уравнение Майера-Касси

Уравнение Касси

Рис

. 1.

Вольтамперная

характеристика

полученная

помощью

уравнения

Майера

Касси

Рис

. 2.

Сравнение

кривых

тока

дуги

Рис

. 3.

Сравнение

кривых

напряжения

дуги

ОБОРУДОВАНИЕ

Page 3

нии с использованием Simulink реализуется прин-

цип визуального программирования, в соответствии

с которым пользователь на экране из библиотеки

стандартных блоков создает модель устройства

и осуществляет расчеты. При этом, в отличие от

классических способов моделирования, пользова-

телю не нужно досконально изучать язык програм-

мирования и численные методы математики, а до-

статочно общих знаний, требующихся при работе на

компьютере и, естественно, знаний той предметной

области, в которой он работает [5].

Таким образом, пользователь при желании может

без особого труда вникнуть в сущность самой модели

и при необходимости модернизировать ее под свою

задачу, добавив один из стандартных элементов.

Готовая модель в трехфазном исполнении пред-

ставляет собой набор из пяти блоков, задание харак-

теристик каждого из которых делает ее полностью

работоспособной. На рисунке 4 изображена сама

модель.

Блок «Система» представляет собой стандартный

блок источника трехфазного напряжения с внутрен-

ним сопротивлением из библиотеки Simulink; блоки

«Питающая сеть» и «Короткая сеть» — трехфазные

RL цепи с заранее определенными величинами ак-

тивного сопротивления и индуктивности. Остальные

блоки были созданы в результате работы:

• блок «ДСП» состоит из функциональных блоков,

описывающих нелинейный характер дуги в ДСП

с возможностью настройки возмущений и систе-

мы регулирования электродов с выбором между

трехфазным и пофазным управлением;

• блок «Печной трансформатор» содержит три

блока однофазных многообмоточных транс-

форматоров с возможностью выбора номера

отпайки и шунтируемых дросселей. Автомати-

ческое изменение коэффициента трансформа-

ции происходит между различными стадиями

плавления, каждая из которых может длиться от

десятков минут до нескольких часов, в то время

как модель рассчитана на работу во временном

промежутке до нескольких секунд. По этой при-

чине было решено отказаться от моделирования

автоматики изменения отпайки печного транс-

форматора, ограничившись возможностью руч-

ного задания.

Настройка параметров блоков осуществляется

через их маски путем задания основных величин

(номера отпайки, паспортных данных, параметров

возмущений и т.д.), что освобождает от необходи-

мости изменять параметры составляющих эле-

ментов.

Разработанная модель позволяет исследовать

любую из стадий работы печи. Однако из практи-

ки известно [1], что наибольшее влияние на пока-

затели качества электроэнергии оказывает именно

этап плавления металла. В отличии от этапа рафи-

нирования, когда электроды работают на ванну уже

расплавленного металла и дуга стабилизирована,

начальный этап плавления характеризуется крайне

нестабильной дугой, низким значением напряже-

ния дуги, частыми короткими замыканиями и обры-

вами. Подобные процессы оказывают негативное

влияние на питающую сеть. Точное предсказание

возникновения места и длительности короткого за-

мыкания или обрыва невозможно, поэтому на прак-

тике принято моделировать подобные возмущения

как колебания изменения реактивной мощности,

потребляемой ДСП, с частотой от 1 до 20 Гц. В ли-

тературе [6, 7] выделяют два основных способа

моделирования: изменение длины дуги по закону

случайного распределения и по синусоиде. В мо-

дели учтены оба варианта, однако именно первый

способ привел к результатам, наиболее близким

к полученным на практике. Однако за пользовате-

лем остается право выбора модели возмущений

в процессе плавки с настройкой частоты и ампли-

туды колебаний.

Трудности при моделировании автоматики

управления положением электродов заключались

в отсутствии наличия в открытом доступе литера-

туры на эту тему. Исходя из теоретических принци-

пов теории автоматического регулирования, был

выведен закон регулирования регуляторов, дей-

ствие которого было направлено на поддержание

заданного сопротивления дуги, вычисляемого из

мгновенных значений токов и напряжений, соответ-

ствующего определенной длине дуги, полученной

из заранее снятых характеристик печи. Несмотря

на то, что в модели регуляторов в явном виде от-

сутствуют исполнительные органы — сервоклапа-

ны, гидроцилиндры и сами двигатели, их влияние

было учтено за счет введения постоянных времени,

создающих необходимую инерцию в процессе регу-

лирования.

Для работы модели необходимо предваритель-

но снять статические характеристики ДСП, к кото-

рым относятся зависимости КПД и коэффициента

мощности, а также регулировочную характеристику,

представляющую собой зависимость сопротивления

дуги от ее длины. С помощью статических характе-

ристик происходит выбор режима работы печи, кото-

рому, в свою очередь, соответствует определенная

длина дуги. Таким образом, определение исходного

режима обеспечивается заданием уставки регулято-

ра по длине дуги.

В разработанной модели регулятора измеритель-

ная и исполнительная части выполнены отдельным

блоком. После измерения тока и напряжения дуги

ДСП происходит расчет сопротивления дуги и пере-

вод его в напряжение в заданном диапазоне значе-

ний. В модель включены фильтры и ограничители,

Рис

. 4.

Модель

ДСП

прилегающей

сети

ПК

Matlab

Печной трансформатор

Короткая сеть

Питающая сеть

Система

ДСП

№

3 (54) 2019

Page 4

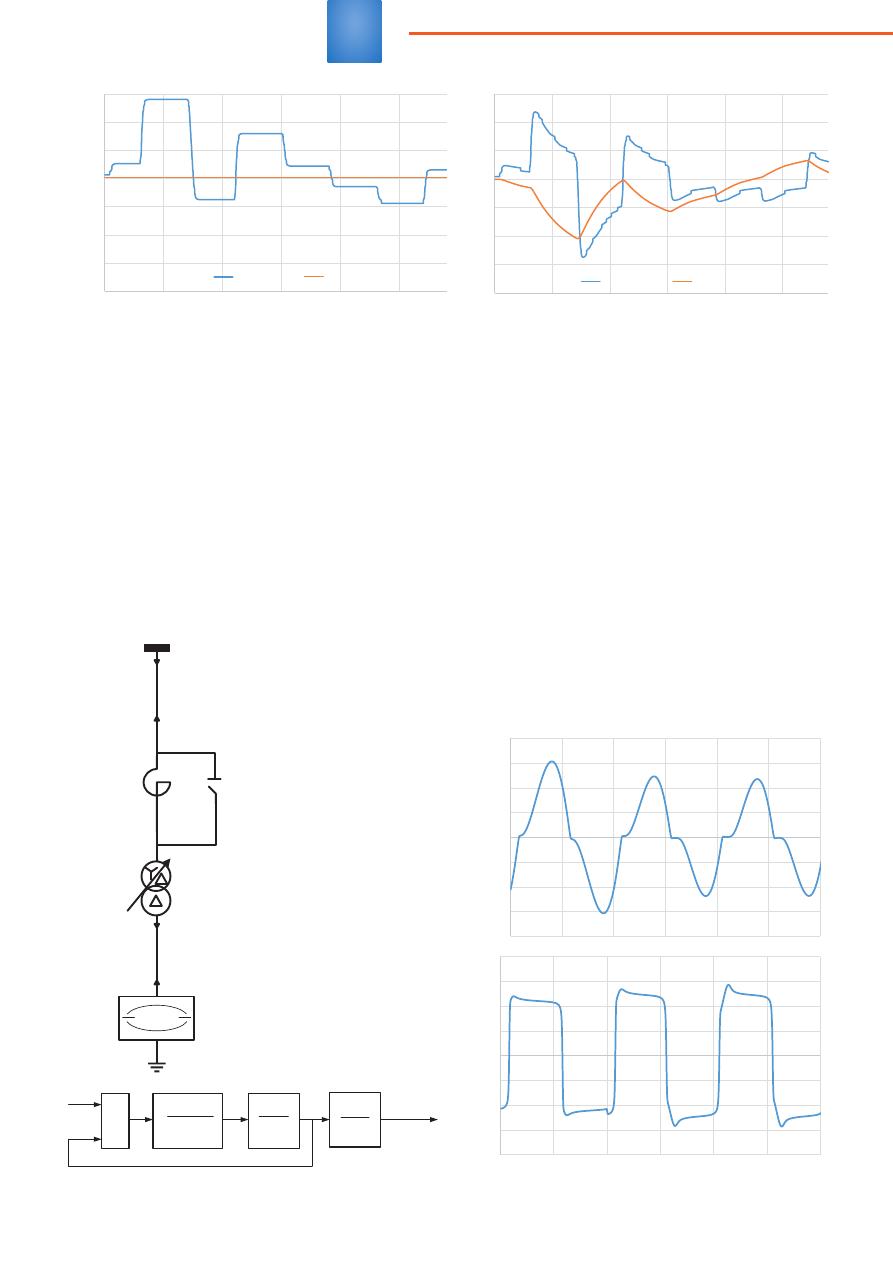
улучшающие процесс регулирования. На рисунке 5

изображено изменение длины дуги под действием

случайных возмущений с частотой 3 Гц и реакция ре-

гулятора в виде кривой управляющего напряжения,

приведенной через коэффициент из области напря-

жений в длину дуги.

В связи с тем, что система регулирования являет-

ся достаточно инерционной и не предназначена для

компенсации колебаний с высокой частотой, посто-

янные времени были подобраны на основании су-

ществующих исследований [8] таким образом, чтобы

процесс регулирования соответствовал реальным

замерам.

Анализ процесса регулирования позволяет сде-

лать вывод о значительном демпфировании коле-

баний длины дуги, что

оказывает значитель-

ное влияние на каче-

ство электроэнергии

[1] и свидетельствует

о необходимости уче-

та в модели.

Последним этапом

при разработке мате-

матической

модели

явилась ее верифика-

ция на основе данных

устройства существу-

ющего предприятия.

Таким образом оце-

нивалась не только

схожесть полученных

результатов с теоре-

тическими, но и до-

статочность данных,

располагаемых предприятием, для успешной работы

с моделью.

При взаимодействии с АО «Металлургический

завод «Электросталь» была организована личная

встреча, включающая в себя экскурсию по предпри-

ятию и выдачу всей необходимой информации для

проведения расчетов. Сотрудники энергетического от-

дела сняли осциллограммы, предоставили паспорт-

ные данные печи и параметры прилегающей сети,

а также параметры настройки регуляторов. Принци-

пиальная схема сети ДСП-20 приведена на рисунке 6.

Помимо этого была получена структурная схема

регулятора, успешно функционирующая на предпри-

ятии. В соответствии с ней разработанная модель

была дополнена одним блоком интегрирования, что

положительно повлияло на процесс регулирования.

Структурная схема регулятора представлена на ри-

сунке 7.

После моделирования схемы сети, изображен-

ной на рисунке 6 с указанием паспортных данных

150

160

170

180

190

200

210

220

0,1

0,6

1,1

1,6

2,1

2,6

мм

, c

Длина дуги

Управляющее напряжение

мм

150

160

170

180

190

200

210

220

0,1

0,6

1,1

1,6

2,1

2,6

Длина дуги

Управляющее напряжение

, c

Рис

. 5.

Изменение

длины

дуги

одной

фазы

ДСП

)

без

регулятора

;

)

регулятором

б)

а)

ÝÒÖÏÊ-13500/35

ÎÑÁ 3õ120
l=90ì

ÂÂÃíã(À)-3x8x1000
l=15ì

ÄÓÄ003202/20

1500/200/100

Рис

. 6.

Принципиальная

схема

электроснабжения

ДСП

-20

T p

Рис

. 7.

Структурная

схема

системы

регулирования

скорости

электродов

ДСП

-20

-80000

-60000

-40000

-20000

20000

40000

60000

80000

1,18

1,19

1,2

1,21

1,22

1,23

1,24

-400

-300

-200

-100

100

200

300

400

1,18

1,19

1,2

1,21

1,22

1,23

1,24

ду

ги

, A

, c

ду

ги

, В

, c

Рис

. 8.

Осциллограммы

токов

напряжений

фазы

ДСП

-20,

рассчитанные

помощью

модели

ОБОРУДОВАНИЕ

Page 5

ДСП и параметров регуляторов, предостав-

ленных АО «Металлургический завод «Элек-

тросталь», были получены кривые измене-

ния токов и напряжения дуги, изображенные

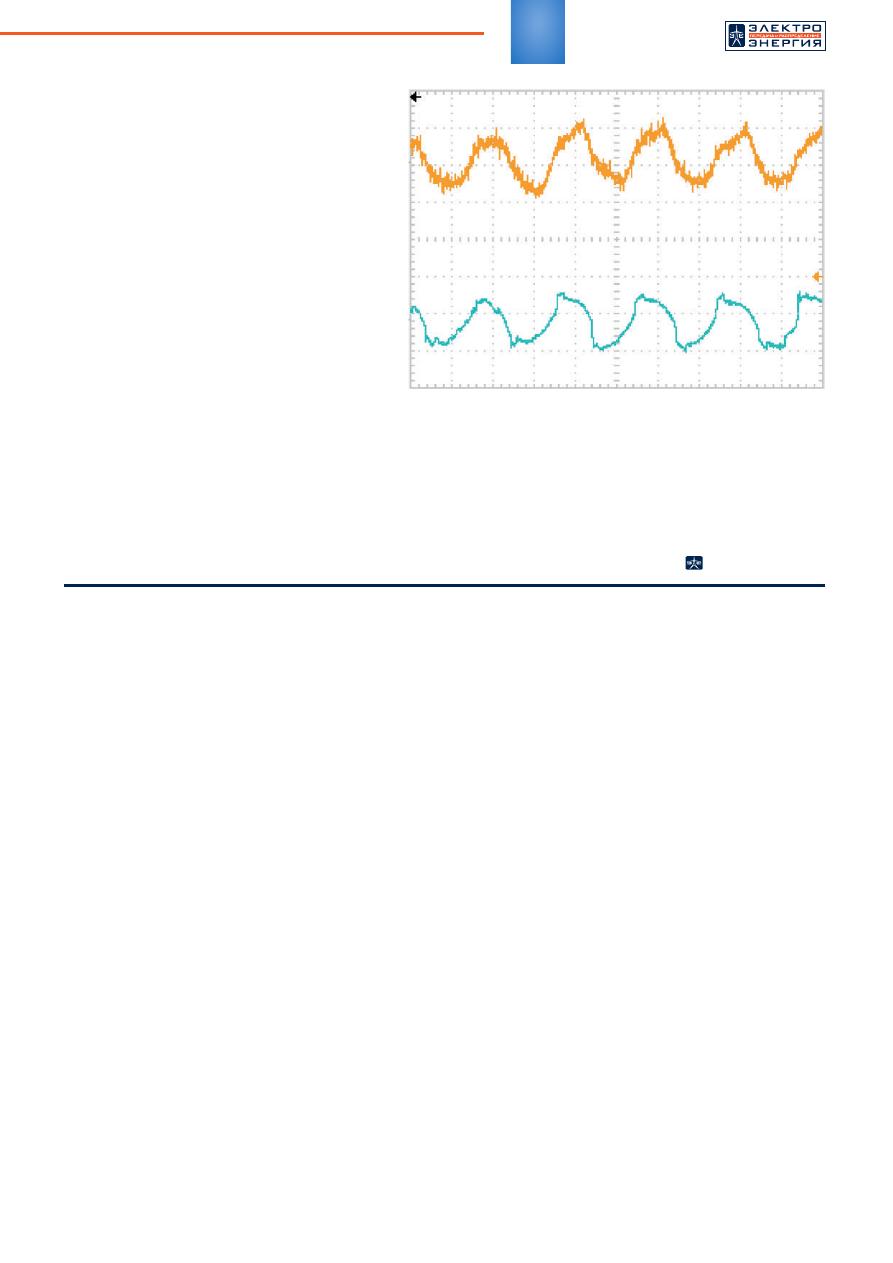
на рисунке 8. На рисун ке 9 приведены ос-

циллограммы токов и напряжений, получен-

ные экспериментально.

Анализ осциллограмм позволяет сделать

вывод о работоспособности модели в связи

с наличием характерных точек как на расчет-

ных, так и на полученных в эксперименте за-

висимостях напряжения. Анализ кривой тока

затруднен большими погрешностями при из-

мерении, возникающими в связи с большим

количеством шумов измерительных преоб-

разователей.

ВЫВОДЫ

Результатом работы явилась верифициро-

ванная модель трехфазной дуговой стале-

плавильной печи со вспомогательными агрегата-

ми и системой регулирования электродов. Модель

была успешно протестирована для оценки рабо-

ты печей на показатели качества электроэнергии

и может быть применена для определения эффек-

тивности применения тех или иных средств для

улучшения этих показателей.

Рис

. 9.

Осциллограммы

токов

напряжений

фазы

ДСП

-20,

снятые

на

предприятии

В настоящее время авторы работы разрабаты-

вают методические указания по работе с моделью,

чтобы максимально облегчить взаимодействие

пользователя, а также планируют адаптировать

под работу с ней один из курсов, преподаваемых

в Ивановском государственном энергетическом

университете им. В.И. Ленина.

ЛИТЕРАТУРА
1. Алиферов А.И. и др. Дуговые

электропечи. Учеб. пособие для

вузов. Новосибирск: Изд-во НГТУ,

2018. 204 с.

2. Фомин А.В. Построение имитаци-

онной модели дуговой сталепла-

вильной печи // Известия ТулГУ.

Технические науки, 2009, № 3.

С. 315–321.

3. Корнилов Г.П., Николаев А.А.,

Храмшин Т.Р., Вахитов Т.Ю.,

Якимов И.А. Особенности мо-

делирования дуговой сталепла-

вильной печи как электротех-

нического комплекса // Вестник

МГТУ им. Г.И. Носова, 2013, № 1.

С. 76–82.

4. Awagan Goyal R., Thosar A.G.

Mathematical Modeling of Electric

Arc Furnace to Study the Flicker.

International Journal of Scientiﬁ c &

Engineering Research, 2016, Vol. 7,

Issue 5, pp. 684-695.

5. Черных И.В. Simulink: Инструмент

моделирования динамических си-

стем. М.: ДМК Пресс, 2008. 288 с.

6. Deepak C. Bhonsle, Ramesh B.

Kelkar. New Time Domain Electric

Arc Furnace Model for Power Quali-

ty Study, 2015. IICPE.

7. Сидорец В.Н., Пентегов И.В. Де-

терминированный хаос в нели-

нейных цепях с электрической

дугой. Киев: Международная ас-

социация «Сварка», 2013. 272 с.

8. Николаев А.А., Корнилов Г.П.,

Тулупов П.Г., Якимов И.А. Разра-

ботка усовершенствованной си-

стемы автоматического управ-

ления положением электродов

дуговых сталеплавильных пе-

чей и агрегатов ковш-печь //

Электротехника: сетевой элек-

тронный журнал, 2014, т. 1, № 1.

С. 48–58.

REFERENCES
1. Aliferov A.I. et alias.

Dugovyye elek -

tropechi

[Electric arc furnaces]. No-

vosibirsk, NGTU Publ., 2018. 204 p.

2. Fomin A.V. Building an electric arc

furnace simulation model.

Izvesti-

ya TulGU. Tekhnicheskiye nauki

[Izvestiya Tula State University.

Technical sciences], 2009, no. 3,

pp. 315–321. (in Russian)

3. Kornilov G.P., Nikolayev A.A.,

Khram shin T.R., Vakhitov T.Yu.,

Yakimov I.A. Modelling features of

an electric arc furnace as electri-

cal equipment.

Vestnik MGTU im.

G.I. Nosova

[The Vestnik of Nosov

Magnitogorsk State Technical Uni-

versity], 2013, no. 1, pp. 76–82. (in

Russian)

4. Awagan Goyal R., Thosar A.G.

Mathematical Modeling of Electric

Arc Furnace to Study the Flicker.

International Journal of Scientiﬁ c &

Engineering Research, 2016, Vol. 7,

Issue 5, pp. 684-695.

5. Chernykh I.V. Simulink:

Instrument

modelirovaniya dinamicheskikh sis -
tem

[Simulink as a dynamic sys-

tems modeling tool]. Moscow, DMK

Press Publ., 2008. 288 p.

6. Deepak C. Bhonsle, Ramesh B.

Kelkar. New Time Domain Electric

Arc Furnace Model for Power Quali-

ty Study, 2015. IICPE.

7. Sidorets V.N., Pentegov I.V.

Deter-

minirovannyy khaos v nelineynykh
tsepyakh s elektricheskoy dugoy

[Deterministic chaos in non-linear

electric arc circuits]. Kyiv, Svarka

Publ., 2013. 272 p.

8. Nikolayev A.A., Kornilov G.P., Tulu-

pov P.G., Yakimov I.A. Development

of an advanced system intended for

automatic control of electric arc fur-

nace electrodes and ladle-furnace

units. Elektrotekhnika: setevoy ele-

ktronnyy zhurnal [Russian Internet

Journal of Electrical Engineering],

2014, vol. 1, no. 1, pp. 48–58. (in

Russian)

№

3 (54) 2019

Оригинал статьи: Разработка математической модели дуговой сталеплавильной печи

Ключевые слова: дуговые сталеплавильные печи, дуга, печь, сталь, математическая модель, ДСП-20, короткая сеть, печной трансформатор

Читать онлайн

Электрические дуговые сталеплавильные печи (ДСП) являются одним из основных агрегатов для плавки высококачественных легированных сталей. Благодаря их ключевым особенностям (быстрому нагреву металлов, возможности поддержания заданной температуры и химического состава) ДСП занимают лидирующие позиции в сталеплавильной индустрии по всему миру. Однако в связи с особенностями технологического процесса дуговые сталеплавильные печи являются потребителем электроэнергии, оказывающим крайне негативное влияние на питающую сеть. В современной российской практике вопросы, связанные с влиянием работы ДСП на показатели качества электроэнергии, обычно решаются эмпирическими методами, не способными в полной мере учесть все особенности процесса. Авторами статьи описывается процесс разработки математической модели, применение которой возможно как на производстве, так и в образовательном процессе.