44
э
н
е
р
г
о
э
ф
ф
е
к
т
и
в
н
о
с
т
ь
энергоэффективность
Прогнозирование
потребления
электроэнергии.
Практика применения
УДК
621.31
Современные
тенденции
развития
рынка
электроэнер
-
гетики
в
Российской
Федерации
характеризуются
по
-
стоянным
ростом
цен
на
ресурсы
,
которые
необходимы
топливно
-
энергетическому
комплексу
для
непрерывного
производства
электроэнергии
,
удорожанием
процесса
возведения
новых
электростанций
и
энергосетей
для
транспортировки
энергии
и
повсеместным
ростом
не
-
платежеспособности
предприятий
-
потребителей
электро
-
энергии
.
Реформирование
РАО
«
ЕЭС
России
»
в
2008
году
привело
всех
участников
образовавшегося
оптового
рынка
электроэнергии
и
мощности
к
необходимости
вы
-
рабатывать
свои
уникальные
стратегии
и
инструменты
использования
энергоресурсов
с
целью
обеспечения
баланса
между
вырабатываемой
и
потребляемой
энерги
-
ей
.
В
данной
статье
производится
сравнение
различных
способов
прогнозирования
потребления
электроэнер
-
гии
с
использованием
алгоритмов
машинного
обучения
и
статистических
методов
на
примере
прогноза
потреб
-
ления
электроэнергии
на
собственные
нужды
ПС
500
кВ
«
Челябинская
»
ПАО
«
ФСК
ЕЭС
».
Мигранов
М
.
М
.,
инженер
1
категории
ОИС
службы
ИС
и
СС
филиала
ПАО
«
ФСК
ЕЭС
» —
МЭС
Урала
,
магистрант
ЧелГУ
Устинов
А
.
А
.,
магистрант
ЧелГУ
Мельников
А
.
В
.,
д
.
т
.
н
.,
профессор
ЧелГУ
Ключевые
слова
:
машинное
обучение
,
электро
-
энергетика
,
прогнозирование
временных
рядов
,
прогнозиро
-
вание
потребления
электро
-
энергии
Keywords:
machine learning, electric
power, time series forecasting,
forecasting of electricity
consumption
ВВЕДЕНИЕ
На
сегодняшний
день
оптовый
рынок
электроэнергии
и
мощности
Россий
-
ской
Федерации
представляет
собой
двухуровневую
систему
—
оптовый
и
розничный
рынки
.
Участниками
дан
-
ного
рынка
являются
генерирующие
компании
(
продавцы
электроэнергии
и
мощности
),
сбытовые
компании
,
сетевые
компании
,
крупные
потре
-
бители
(
покупатели
электроэнергии
и
мощности
).
На
оптовом
рынке
элек
-
троэнергии
функционирует
несколько
секторов
,
различаются
они
условиями
заключения
сделок
и
сроками
постав
-
ки
:
сектор
регулируемых
договоров
,
сектор
свободных
договоров
,
рынок
на
сутки
вперед
(
РСВ
),
балансирую
-
щий
рынок
(
БР
).
Основной
объем
производимой
электроэнергии
продается
в
одном
секторе
,
который
и
формирует
пла
-
новое
потребление
, —
рынок
на
сутки
вперед
(
РСВ
).
На
РСВ
коммерческий
оператор
ОАО
«
АТС
»
проводит
кон
-
курентный
отбор
ценовых
заявок
по
-
ставщиков
и
покупателей
за
сутки
до

45
реальной
поставки
электроэнергии
с
определением
цен
и
объемов
поставки
на
каждый
час
суток
.
Однако
фактическое
потребление
неизбежно
отличается
от
планового
,
и
именно
поэтому
был
создан
баланси
-
рующий
рынок
.
На
БР
осуществляется
торговля
от
-
клонениями
от
планового
производства
/
потребления
в
режиме
реального
времени
.
В
сложившихся
рыночных
условиях
ценообразо
-
вывающим
фактором
электроэнергии
при
расчете
конечной
цены
отпуска
ее
потребителям
для
энер
-
госбытовой
компании
является
ее
стоимость
приоб
-
ретения
на
РСВ
.
При
данном
факторе
использова
-
ние
актуальных
методов
прогнозирования
,
а
также
современного
программного
обеспечения
совместно
с
системами
автоматизированного
контроля
учета
электроэнергии
(
АСКУЭ
)
представляет
стратегиче
-
ский
и
экономический
интересы
.
Отличие
цен
элек
-
троэнергии
на
БР
от
РСВ
в
Российской
Федерации
составляет
15–40%.
Постоянно
изменяющиеся
условия
рынка
,
объемы
покупаемой
энергии
и
объемы
энергии
для
транспор
-
тировки
создают
необходимость
сетевым
организаци
-
ям
в
прогнозировании
:
количества
энергии
,
которую
необходимо
поставить
потребителям
;
нагрузки
на
се
-
тевые
мощности
организации
;
вероятности
возникно
-
вения
поломок
на
линиях
передачи
;
количества
энер
-
гозатрат
на
собственные
нужды
для
поддержания
основной
хозяйственной
деятельности
.
Из
перечисленного
выше
следует
,
что
получение
максимально
возможной
точности
построения
про
-
гнозов
с
помощью
используемых
прогностических
моделей
энергопотребления
представляет
экономи
-
ческий
интерес
как
для
сетевых
,
так
и
для
сбытовых
компаний
.
Актуальность
задачи
прогнозирования
потре
-
бления
электроэнергии
для
отечественной
электро
-
энергетики
подтверждается
и
обширным
списком
научных
работ
,
проведенных
российскими
иссле
-
дователями
.
Следует
отметить
следующие
работы
,
опубликованные
за
последние
годы
:
Грицай
А
.
С
.
«
Гиб
ридный
метод
краткосрочного
прогнозирования
потребления
электрической
энергии
для
энергос
-
бытового
предприятия
с
учетов
метеофкаторов
»,
2017
г
.;
Абдурахманов
А
.
М
. «
Методы
прогнозиро
-
вания
электропотребления
в
распределительных
сетях
», 2016
г
.;
Соломахо
К
.
Л
«
Применение
метода
главных
компонент
для
прогнозирования
объемов
электропотребления
энергосбытового
предпри
-
ятия
», 2015
г
.;
Хуссейн
А
.
З
. «
Повышение
точности
краткосрочного
прогнозирования
электрической
на
-
грузки
потребителей
региона
с
учетом
метеофакто
-
ров
на
основе
метода
опорных
векторов
», 2015
г
.;
Кошарная
Ю
.
В
. «
Разработка
методики
анализа
па
-
раметров
электропотребления
для
их
нормирова
-
ния
и
оценки
объемов
энергосбережения
при
про
-
ведении
энергоаудита
предприятий
и
организаций
»,
2015
г
.;
Гарифуллин
Ш
.
Р
. «
Прогнозирование
потре
-
бления
электроэнергии
с
помощью
методов
машин
-
ного
обучения
», 2015
г
.;
Гофман
А
.
В
. «
Моделиро
-
вание
электропотребления
многономенклатурного
предприятия
для
краткосрочного
прогнозирования
»,
2013
г
.;
Белов
К
.
И
. «
Автоматизированная
система
прогнозирования
потребления
электрической
энер
-
гии
предприятием
», 2012
г
.;
Валь
П
.
В
. «
Краткосроч
-
ное
прогнозирование
электропотребления
горного
предприятия
в
условиях
оптового
рынка
электро
-
энергии
и
мощности
», 2012
г
.;
Бажинов
А
.
Н
. «
Метод
прогнозирования
объемов
потребления
электро
-
энергии
предприятием
черной
металургии
на
основе
нейро
-
нечетких
алгоритмов
», 2011
г
.;
Анушина
Е
.
С
.
«
Система
краткосрочного
прогнозирования
электри
-
ческой
нагрузки
», 2009
г
.;
Гордеев
А
.
С
. «
Прогнозиро
-
вание
электропотребления
объектов
с
применением
искусственных
нейронных
сетей
», 2008
г
.
ЗАДАЧА
Объект
исследования
—
объекты
электросетевого
хозяйства
ПАО
«
ФСК
ЕЭС
».
Предмет
исследования
—
потребление
электро
-
энергии
на
собственные
нужды
субъектами
электро
-
сетевого
хозяйства
предприятия
,
модели
и
методы
краткосрочного
прогнозирования
потребления
элек
-
троэнергии
.
Цель
исследования
—
сравнение
методов
кратко
-
срочного
прогнозирования
потребления
электро
-
энергии
для
объектов
электросетевого
хозяйства
ПАО
«
ФСК
ЕЭС
».
Задачи
исследования
:
1)
провести
обзор
методов
прогнозирования
вре
-
менных
рядов
;
2)
провести
отбор
алгоритмов
для
построения
моде
-
лей
прогнозирования
потребления
электроэнергии
;
3)
подготовить
данные
для
составления
краткосроч
-
ного
прогноза
потребления
электроэнергии
;
4)
подготовить
прогнозные
модели
;
5)
провести
сравнение
результатов
прогнозных
мо
-
делей
.
В
качестве
опорных
данных
будут
использованы
данные
потребления
,
взятые
из
АИИС
КУЭ
четы
-
рех
ТСН
0,4
кВ
ПС
500
кВ
«
Челябинская
»
за
период
с
01.01.2014
по
06.11.2017.
Для
хранения
и
предо
-
бработки
расчетных
данных
используются
библиоте
-
ки
pandas, numpy, autocleaner,
для
расчетов
исполь
-
зуются
библиотеки
машинного
обучения
xgboost,
scikit-learn, statsmodels, seasonals.
Визуализация
выполнена
при
помощи
библиотек
matplotlib.pyplot,
seaborn, plotly.
1.
Обзор
методов
прогнозирования
временных
рядов
Для
начала
необходимо
ввести
определение
вре
-
менного
ряда
.
Временной
ряд
—
это
последовательность
зна
-
чений
,
описывающих
протекающий
во
времени
про
-
цесс
,
измеренных
в
последовательные
моменты
времени
,
обычно
через
равные
промежутки
[1].
Используемые
для
целей
и
задач
прогнозирова
-
ния
временные
ряды
экономических
показателей
об
-
ладают
рядом
особенностей
.
Так
как
временной
ряд
является
последовательностью
значений
,
в
котором
каждое
следующее
значение
содержит
в
себе
про
-
шлое
для
последующих
,
то
любая
попытка
прогнози
-
ровать
будущее
без
исследования
временных
рядов
прошлого
является
ненаучной
и
ошибочной
.
Поэто
-
му
для
получения
достаточно
точных
и
надежных
прогнозов
необходимо
подробно
изучить
настоящее
№
2 (47) 2018
46
состояние
явления
или
процесса
.
Например
,
раз
-
ложить
ряд
на
составные
компоненты
и
устранить
влияние
систематических
компонент
на
изменение
случайных
,
проверить
ряд
на
наличие
основной
тен
-
денции
и
при
наличии
таковой
провести
ее
выде
-
ление
,
выявить
тренд
и
его
направление
(
критерий
Аббе
-
Линника
,
критерий
Кокса
-
Стюарта
,
критерий
Фостера
-
Стюарта
),
определить
сезонность
(
мульти
-
пликативная
или
аддитивная
),
избавить
ряд
от
не
-
стационарности
(
взятие
разностей
,
преобразование
Бокса
-
Кокса
).
Выявление
указанных
параметров
временного
ряда
очень
важно
для
выбора
после
-
дующей
модели
прогнозирования
и
без
проведения
предварительного
анализа
невозможно
построить
качественную
модель
.
Метод
средних
Воспользуемся
наивным
предположением
,
что
«
завтра
будет
,
как
вчера
»,
однако
примем
утверждение
,
что
будущее
потре
-
бление
зависит
от
среднего
n
его
предыдущих
значений
,
а
значит
,
воспользуемся
скользящей
сред
-
ней
[2].
Сделать
такой
прогноз
долго
-
срочным
не
удастся
—
для
полу
-
чения
прогноза
на
период
вперед
необходимо
,
чтобы
предыдущий
период
был
фактически
наблю
-
даемым
.
Однако
скользящую
среднюю
можно
использовать
и
для
другой
цели
—
сглаживания
исходного
ряда
для
выявления
тренда
.
Чем
больше
будет
ширина
,
тем
более
сглаженным
будет
тренд
.
В
на
-
шем
случае
тренды
очевидны
,
и
сглаживание
по
неделям
и
ме
-
сяцам
лишь
сгладит
общий
гра
-
фик
потребления
(
рисунки
1
и
2).
Модификацией
простой
скользящей
средней
является
так
называемая
взвешенная
средняя
,
внутри
которой
наблю
-
дениям
придаются
различные
веса
,
в
сумме
дающие
едини
-
цу
,
при
этом
обычно
последним
наблюдениям
присваивается
больший
вес
.
Подобная
модель
обладает
возможностью
на
-
стройки
в
сравнении
с
простой
моделью
скользящей
средней
.
Экспоненциальные
сглаживания
Взвесим
все
доступные
на
-
блюдения
,
экспоненциально
уменьшая
веса
по
мере
углубле
-
ния
в
исторические
данные
.
Для
этого
воспользуемся
формулой
простого
экспоненциального
сгла
-
живания
[3]:
t
=
yt
+ (1
–
)
t
– 1.
Здесь
значение
прогноза
представляет
собой
средневзвешенную
между
текущим
истинным
и
пре
-
дыдущим
модельным
значениями
.
—
сглажива
-
ющий
фактор
.
С
его
помощью
определяется
,
как
быстро
будет
«
забываться
»
последнее
доступное
на
-
блюдение
.
Чем
меньше
сглаживающий
фактор
,
тем
больше
влияния
оказывают
предыдущие
модельные
значения
,
и
тем
сильнее
сглаживается
ряд
.
В
данном
случае
экспоненциальность
модели
в
ее
рекурсивности
—
каждый
раз
мы
умножаем
(1 –
)
на
предыдущее
модельное
значение
,
которое
также
со
-
держало
в
себе
(1 –
),
и
так
до
начала
наблюдений
(
рисунок
3).
Изменяя
вес
,
мы
можем
добиться
приемлемого
качества
прогноза
,
однако
,
как
и
модель
скользящей
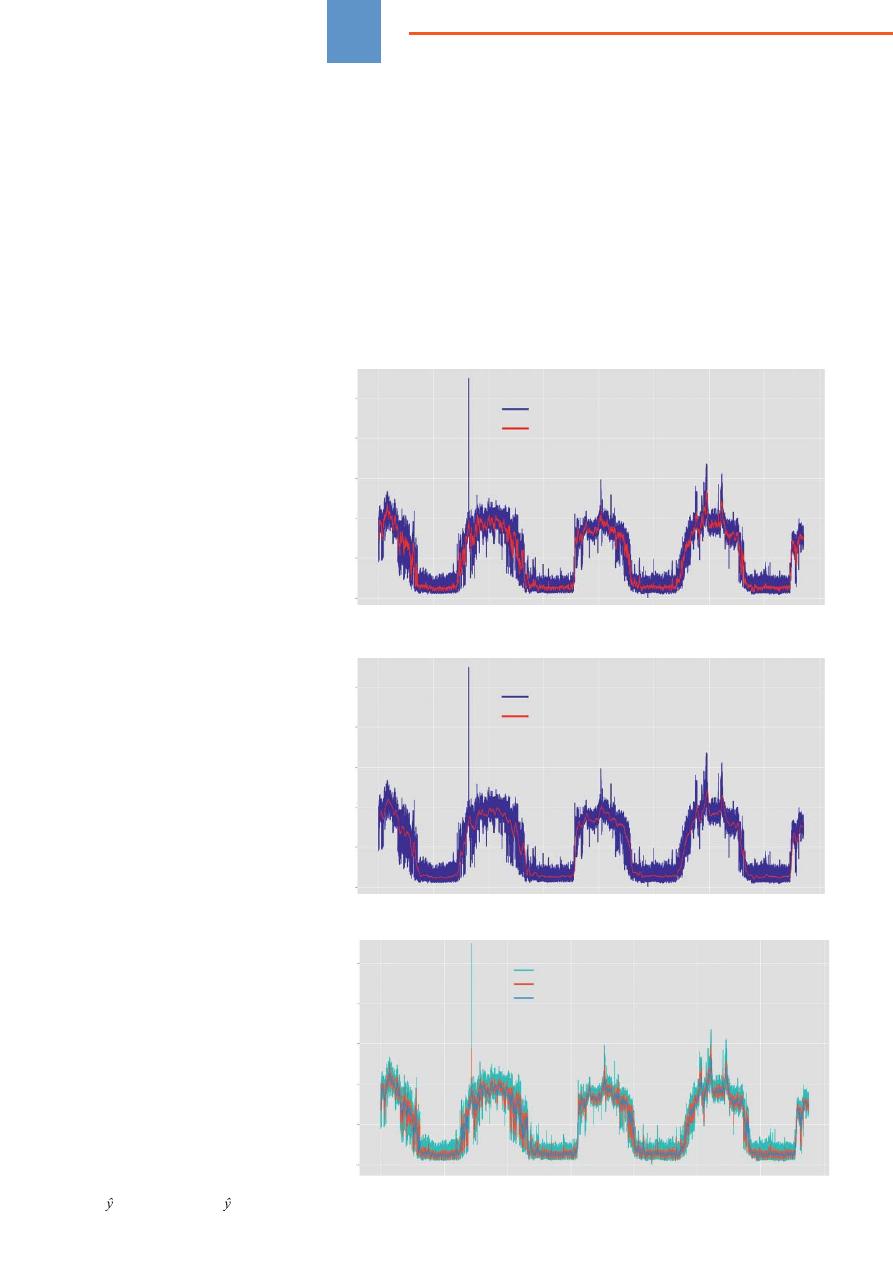
Рис
. 1.
Суточный
тренд
Рис
. 2.
Недельный
тренд
Дата
По
тре
бление
,
кВ
/
ч
2014-01
1000
800
600
400
200
0
2014-07
2015-01
2015-06
2016-01
2016-07
2017-01
2017-07
2018-01
Реальное
потребление
Скользящая
средняя
тренда
Дата
По
тре
бление
,
кВ
/
ч
2014-01
1000
800
600
400
200
0
2014-07
2015-01
2015-06
2016-01
2016-07
2017-01
2017-07
2018-01
Реальное
потребление
Скользящая
средняя
тренда
Рис
. 3.
Экспоненциальное
сглаживание
Наблюдения
По
тре
бление
,
кВ
/
ч
0
5000
1000
800
600
400
200
0
10000
15000
20000
25000
30000
35000
Реальное
потребление
= 0,3
= 0,05
ЭНЕРГО-
ЭФФЕКТИВНОСТЬ
47
и
взвешенной
средней
,
такая
мо
-
дель
позволяет
делать
прогноз
лишь
на
одну
точку
вперед
,
что
явно
недостаточно
для
решения
задачи
прогнозирования
потре
-
бления
электроэнергии
.
Разобьем
ряд
на
две
составля
-
ющие
—
уровень
l
и
тренд
.
Уро
-
вень
(
ожидаемое
значение
ряда
)
мы
предсказывали
с
помощью
вышеописанных
моделей
,
теперь
же
применим
экспоненциальное
сглаживание
к
тренду
,
полагая
,
что
будущее
направление
изме
-
нения
ряда
зависит
от
взвешен
-
ных
предыдущих
изменений
[3]:
l
x
=
y
x
+ (1 –
) (
l
x
– 1
+
b
x
– 1
);
b
x
=
(
l
x
–
l
x
– 1
) + (1 –
)
b
x
– 1
;
x
+ 1
=
l
x
+
b
x
.
Результатом
такого
разбиения
является
набор
функций
.
Первая
из
них
описывает
уровень
,
завися
-
щий
,
как
и
прежде
,
от
текущего
значения
ряда
,
а
вто
-
рое
слагаемое
разбивается
на
предыдущее
значение
уровня
и
тренда
.
Вторая
функция
отвечает
за
тренд
,
зависящий
от
изменения
уровня
на
текущем
шаге
и
от
предыдущего
значения
тренда
.
Финальный
про
-
гноз
является
суммой
модельных
значений
уровня
и
тренда
(
рисунок
4).
Сочетание
параметров
и
позволяет
тонко
на
-
строить
модель
двойного
экспоненциального
сглажи
-
вания
.
Первый
отвечает
за
сглаживание
ряда
трен
-
да
,
второй
—
за
сглаживание
самого
тренда
.
Чем
выше
значения
,
тем
больший
вес
будет
у
последних
наблюдений
,
и
тем
менее
будет
сглаживаться
мо
-
дельный
ряд
.
Модель
двойного
экспоненциального
сглаживания
позволяет
делать
прогноз
сразу
на
два
периода
вперед
.
Теперь
добавим
третью
компоненту
—
сезон
-
ность
.
Стоит
оговориться
,
что
данный
метод
при
-
меним
лишь
в
случае
,
когда
исходный
ряд
обладает
сезонностью
,
что
справедливо
для
исходных
данных
эксперимента
.
Данная
компонента
объяснит
повто
-
ряющие
колебания
вокруг
уровня
и
тренда
,
а
харак
-
теризуется
она
длиной
сезона
—
периодом
,
после
которого
начинаются
повторения
колебаний
.
Для
каждого
наблюдения
в
сезоне
формируется
своя
компонента
,
например
,
если
длина
сезона
составля
-
ет
7 (
к
примеру
,
сезонная
компонента
),
то
получим
7
сезонных
компонент
.
Получим
новую
систему
:
l
x
=
(
y
x
–
s
x
–
L
) + (1 –
) (
l
x
– 1
+
b
x
– 1
);
b
x
=
(
l
x
–
l
x
– 1
) + (1 –
)
b
x
– 1
;
s
x
=
(
y
x
–
l
x
) + (1 –
)
s
x
–
L
;
x
+
m
=
l
x
+
m
b
x
+
s
x
–
L
+ 1 + (
m
– 1)
mod
L
.
Уровень
теперь
зависит
от
текущего
значения
ряда
за
вычетом
соответствующей
сезонной
компоненты
,
тренд
остается
без
изменений
,
а
сезонная
компонен
-
та
зависит
от
текущего
значения
ряда
за
вычетом
уровня
и
от
предыдущего
значения
компоненты
.
При
этом
компоненты
сглаживаются
через
все
доступные
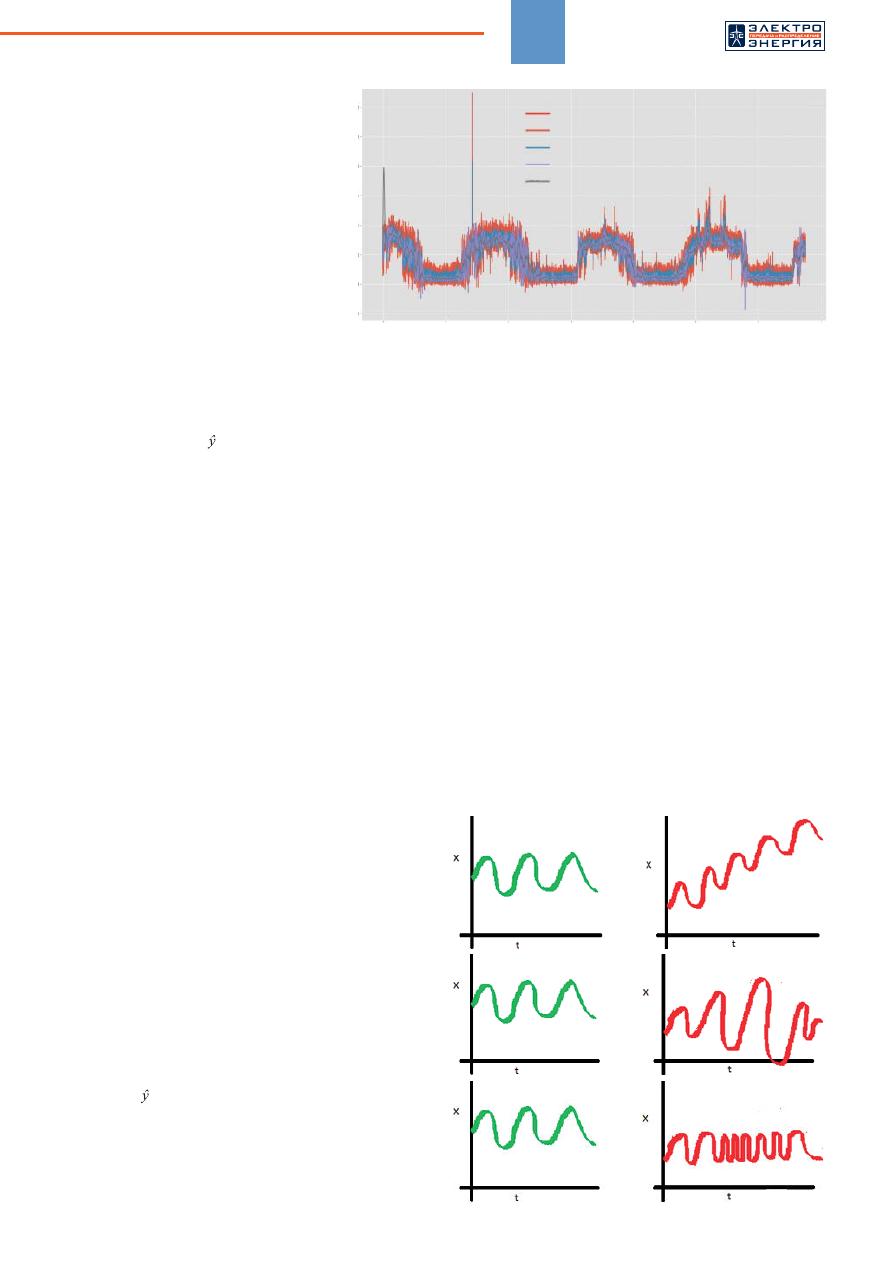
Рис
. 4.
Двойное
экспоненциальное
сглаживание
Наблюдения
По
тре
бление
,
кВ
/
ч
0
5000
1500
1250
1000
750
500
250
0
-250
10000
15000
20000
25000
30000
35000
Реальное
потребление
= 0,9,
= 0,9
= 0,9,
= 0,02
= 0,02,
= 0,9
= 0,02,
= 0,02
Рис
. 5.
Сравнение
стационарных
и
нестационарных
рядов
Стационарные
ряды
Нестационарные
ряды
сезоны
,
например
,
если
это
компонента
,
отвечающая
за
понедельник
,
то
и
усредняться
она
будет
только
с
другими
понедельниками
.
Теперь
,
имея
сезонную
компоненту
,
появляется
возможность
делать
прогноз
на
произвольное
количество
(
m
)
шагов
.
Получившаяся
модель
называется
моделью
трой
-
ного
экспоненционального
сглаживания
или
моде
-
лью
Хольта
-
Винтерса
[4].
Следует
отметить
,
что
качество
моделей
,
осно
-
ванных
на
экспоненциальном
сглаживании
,
сильно
зависит
от
подбора
коэффициентов
,
размерности
исходных
данных
,
зашумленности
данных
,
сезонно
-
сти
и
т
.
д
.
Эконометрический
подход
Перед
тем
как
перейти
к
использованию
экономе
-
трического
подхода
,
определим
понятие
стационар
-
ности
.
Под
стационарностью
понимают
свойство
про
-
цесса
не
менять
своих
статистических
характеристик
с
течением
времени
(
постоянство
математического
ожидания
,
гомоскедастичность
)
и
независимость
ко
-
вариационной
функции
от
времени
(
рисунок
5) [5].
№
2 (47) 2018

48
В
чем
заключается
важность
стационарности
?
Большинство
моделей
временных
рядов
модели
-
руют
математическое
ожидание
либо
дисперсию
,
и
в
случае
нестационарности
ряда
предсказания
бу
-
дут
неверными
.
Определим
понятие
ARIMA.
ARIMA (
англ
. autoregressive integrated moving
average,
иногда
модель
Бокса
-
Дженкинса
,
методо
-
логия
Бокса
-
Дженкинса
) —
интегрированная
модель
авторегрессии
—
скользящего
среднего
—
модель
и
методология
анализа
временных
рядов
.
Является
расширением
моделей
ARMA
для
нестационарных
временных
рядов
,
которые
можно
сделать
стацио
-
нарными
взятием
разностей
некоторого
порядка
от
исходного
временного
ряда
(
так
называемые
инте
-
грированные
или
разностно
-
стационарные
времен
-
ные
ряды
) [6].
SARIMA
является
модификацией
модели
ARIMA
(
так
называемая
Seasonal ARIMA).
Общий
вид
мо
-
дели
ARIMA(
p,d,q
)(
P,D,Q
)
.
В
этой
модели
параметры
обозначают
следующее
:
p
—
порядок
модели
AR(
p
);
d
—
порядок
интегрирования
исходных
данных
;
q
—
порядок
модели
MA(
q
);
P
—
порядок
сезонной
составляющей
SAR(
P
);
D
—
порядок
интегрирования
сезонной
составляющей
;
Q
—
порядок
сезонной
составляющей
SMA(
Q
);
s
—
размерность
сезонности
(
месяц
,
квартал
и
т
.
д
.).
Регрессионные
модели
Регрессионные
алгоритмы
являются
моделью
обучения
с
учителем
,
когда
на
вход
алгоритма
пода
-
ется
обучающая
выборка
,
содержащая
ряд
призна
-
ков
и
переменную
,
соответствующую
этому
ряду
.
В
ходе
обучения
модель
подбирает
коэффициенты
формулы
регрессии
и
в
дальнейшем
может
строить
прогноз
на
произвольное
количество
шагов
.
Однако
сама
логика
временного
ряда
состоит
в
том
,
чтобы
мы
опирались
на
предыдущее
значение
,
прогнози
-
руя
текущее
.
Таким
образом
,
одним
из
ключевых
признаков
для
обучения
прогнозных
моделей
с
ис
-
пользованием
регрессионных
алгоритмов
является
разница
между
текущим
и
предыдущим
значением
или
лаг
.
Используемая
в
статистике
регрессионная
модель
зависимости
одной
(
объясняемой
,
зави
-
симой
)
переменной
y
от
другой
или
нескольких
других
переменных
(
факторов
,
регрессоров
,
неза
-
висимых
переменных
)
x
с
линейной
функцией
за
-
висимости
.
Модель
линейной
регрессии
является
часто
используемой
и
наиболее
изученной
в
эко
-
нометрике
.
А
именно
изучены
свойства
оценок
параметров
,
получаемых
различными
методами
при
предположениях
о
вероятностных
характе
-
ристиках
факторов
,
и
случайных
ошибок
модели
.
Предельные
(
асимптотические
)
свойства
оценок
нелинейных
моделей
также
выводятся
исходя
из
аппроксимации
последних
линейными
моделями
.
Необходимо
отметить
,
что
с
эконометрической
точки
зрения
более
важное
значение
имеет
ли
-
нейность
по
параметрам
,
чем
линейность
по
фак
-
торам
модели
[10].
Однако
линейная
регрессия
очень
чувствительна
к
выбросам
,
которые
сильно
искажают
ее
результаты
.
Робастные
методы
представляют
собой
форму
регрессионного
анализа
,
разработанную
для
пре
-
одоления
некоторых
ограничений
традиционных
параметрических
и
непараметрических
методов
.
На
практике
наличие
в
выборках
даже
небольшого
числа
резко
выделяющихся
наблюдений
(
выбро
-
сов
)
способно
сильно
повлиять
на
результат
иссле
-
дования
,
например
,
метод
наименьших
квадратов
и
метод
максимального
правдоподобия
подверже
-
ны
такого
рода
искажениям
,
и
значения
,
получае
-
мые
в
результате
исследования
,
могут
перестать
нести
в
себе
какой
-
либо
смысл
.
Для
исключения
влияния
таких
помех
используются
различные
под
-
ходы
для
снижения
влияния
«
плохих
»
наблюдений
(
выбросов
),
либо
полного
их
исключения
.
Основ
-
ная
задача
робастных
методов
—
отличить
«
пло
-
хое
»
наблюдение
от
«
хорошего
» [11].
Широкое
распространение
получили
методы
,
основанные
на
алгоритмах
решающих
деревьев
.
Структура
дерева
представляет
собой
«
листья
»
и
«
ветки
».
На
ребрах
(«
ветках
»)
дерева
решения
записаны
атрибуты
,
от
которых
зависит
целевая
функция
,
в
«
листьях
»
записаны
значения
целевой
функции
,
а
в
остальных
узлах
—
атрибуты
,
по
кото
-
рым
различаются
случаи
.
Чтобы
классифицировать
новый
случай
,
надо
спуститься
по
дереву
до
листа
и
выдать
соответствующее
значение
.
Подобные
де
-
ревья
решений
широко
используются
в
интеллекту
-
альном
анализе
данных
.
Цель
состоит
в
том
,
чтобы
создать
модель
,
которая
предсказывает
значение
целевой
переменной
на
основе
нескольких
перемен
-
ных
на
входе
[12].
Также
часто
используются
так
называемые
ан
-
самблевые
методы
,
суть
которых
в
построении
сильного
ансамбля
из
простых
моделей
.
Напри
-
мер
,
решающий
лес
на
основе
решающих
деревьев
либо
алгоритмы
на
основе
бустинга
,
в
основе
ко
-
торого
процедура
последовательного
построения
композиции
алгоритмов
машинного
обучения
,
когда
каждый
следующий
алгоритм
стремится
компенси
-
ровать
недостатки
композиции
всех
предыдущих
алгоритмов
[13].
Для
исследования
были
отобраны
регрессион
-
ные
алгоритмы
из
состава
открытой
библиотеки
sklearn (Bayesian Ridge, Elastic Net CV, Huber Re-
gressor, Lasso Lars CV, Orthogonal Matching Pursuit
CV, Linear Regression, DecisionTreeRegressor, Extra-
TreesRegressor, RandomForestRegressor)
и
библио
-
теки
xgboost (XGBRegressor).
2.
Подготовка
данных
для
прогнозирования
потребления
электроэнергии
при
помощи
модели
ARIMA
Главным
условием
использования
модели
ARIMA
является
стационарность
временного
ряда
.
Для
про
-
верки
ряда
на
стационарность
воспользуемся
рас
-
ширенным
тестом
Дики
-
Фуллера
[14].
Результаты
проверки
приведены
на
рисунке
6.
Критерий
Дики
-
Фуллера
для
исходного
ряда
со
-
ставил
p
= 0,1649,
и
не
отверг
нулевую
гипотезу
о
нестационарности
.
Применим
к
исходному
ряду
преобразования
Бокса
-
Кокса
для
стабилизирования
дисперсии
(
рисунок
7).
ЭНЕРГО-
ЭФФЕКТИВНОСТЬ
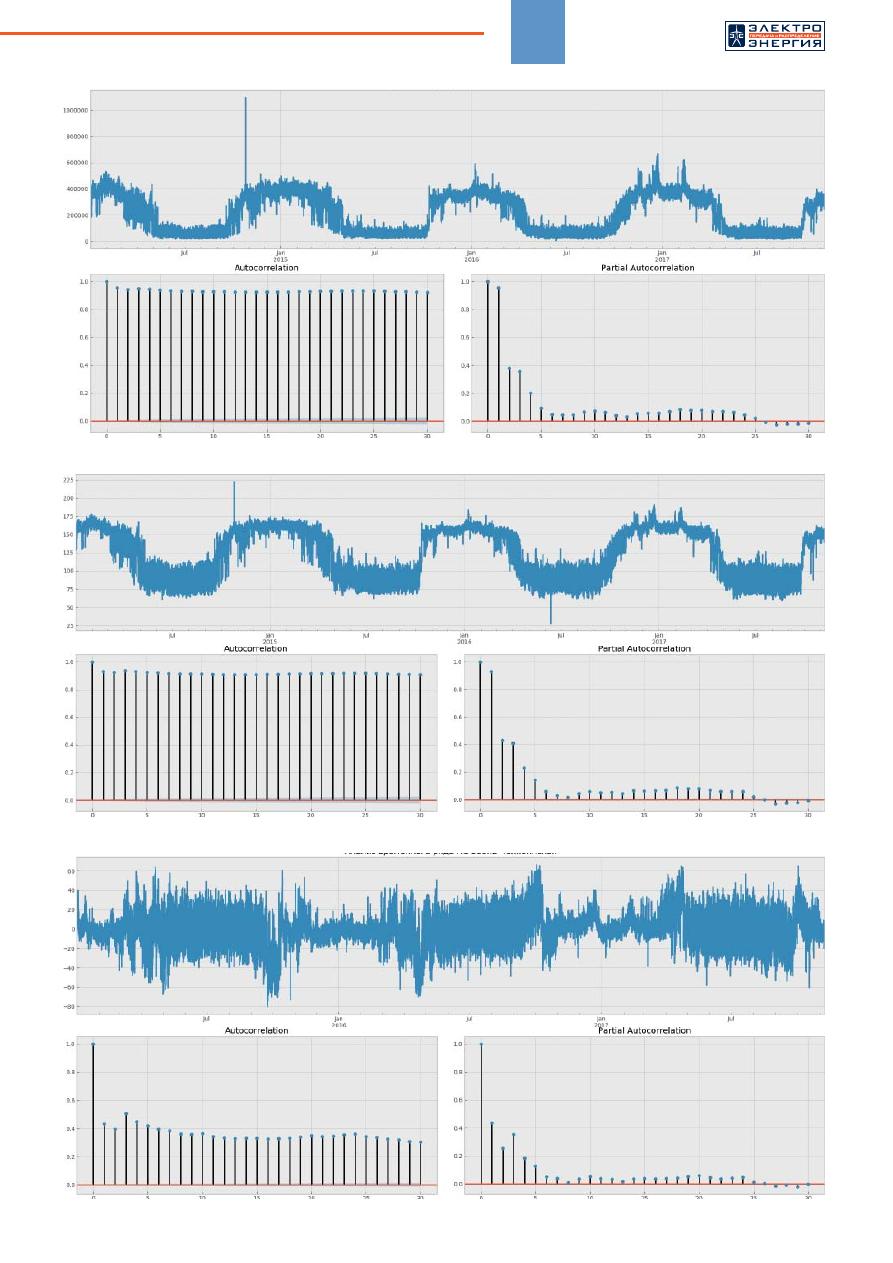
49
Рис
. 6.
Проверка
ряда
на
стационарность
Рис
. 7.
Преобразования
Бокса
-
Кокса
для
стабилизирования
дисперсии
Рис
. 8.
Проверка
ряда
на
стационарность
с
учетом
сезонной
разницы
№
2 (47) 2018
50
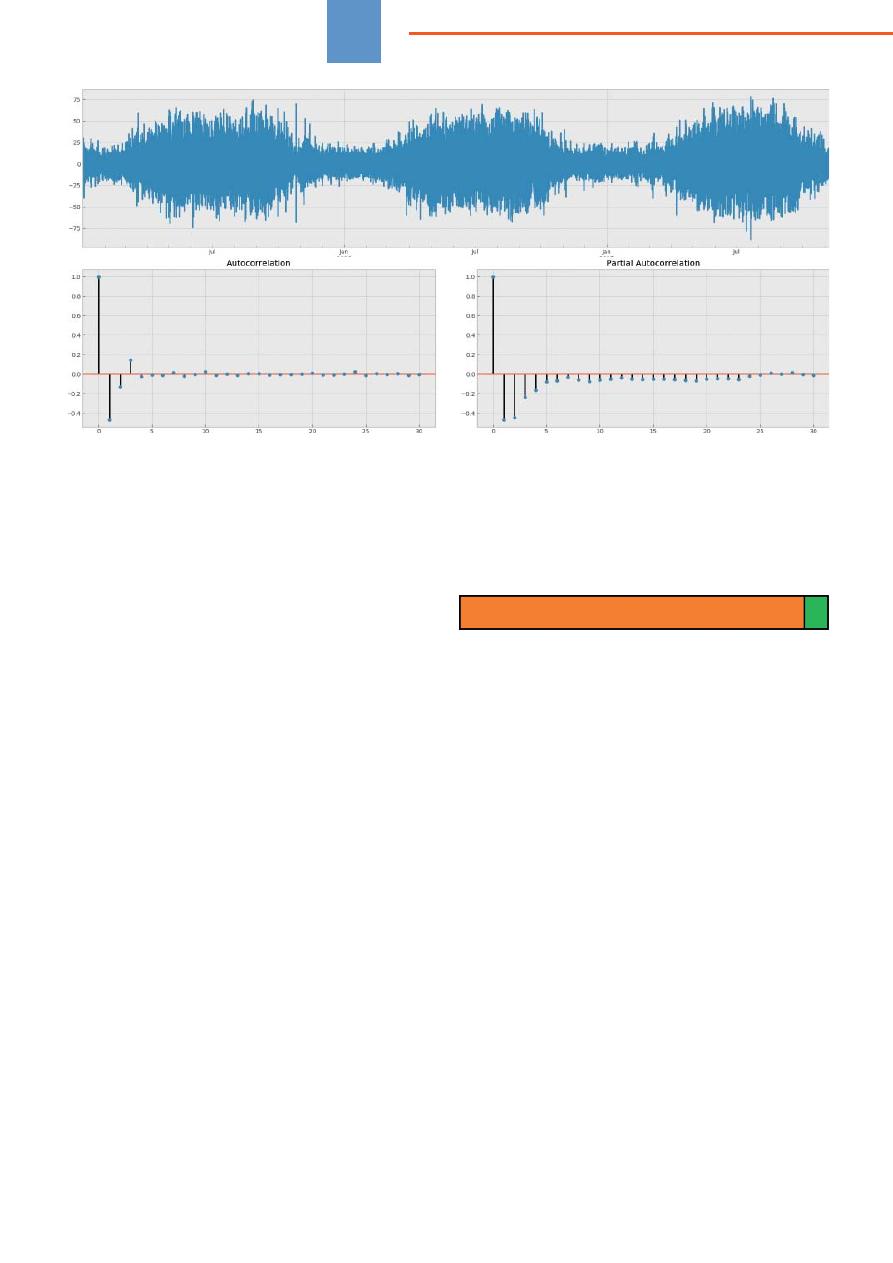
Критерий
Дики
-
Фуллера
снизился
до
0,13
и
все
еще
не
отвергает
нулевую
гипотезу
о
наличии
еди
-
ничного
корня
.
Возьмем
сезонные
разницы
и
прове
-
дем
тест
еще
раз
(
рисунок
8).
Критерий
Дики
-
Фуллера
стал
равняться
нулю
,
та
-
ким
образом
,
гипотеза
о
нестационарности
опровер
-
гнута
,
однако
график
автокорреляционной
функции
показывает
слишком
много
значимых
лагов
.
Попро
-
буем
взять
первые
разницы
и
привести
ряд
к
стацио
-
нарному
виду
(
рисунок
9).
Получившийся
ряд
стационарен
,
его
можно
ис
-
пользовать
для
построения
прогнозной
модели
с
ис
-
пользованием
метода
ARIMA.
3.
Подготовка
данных
для
прогнозирования
потребления
электроэнергии
с
использованием
алгоритмов
машинного
обучения
В
качестве
регулярных
признаков
датасета
были
взяты
календарные
значения
,
а
именно
:
a.
Час
(int64)
b.
День
в
году
(int64)
c.
День
недели
(int64)
d.
Неделя
в
году
(int64)
e.
Месяц
(int64)
f.
Будни
/
выходной
(int64)
Признаки
были
закодированы
целочисленными
значениями
,
но
так
как
использовать
категориальные
переменные
в
моделях
регрессии
нежелательно
,
ка
-
тегориальные
признаки
заменены
средним
потребле
-
нием
за
каждую
выбранную
единицу
времени
.
Также
в
качестве
нерегулярных
признаков
используются
лаги
—
сдвиг
временного
ряда
,
позволяющий
исполь
-
зовать
данные
потребления
прошлых
периодов
.
Признаки
:
a.
Среднечасовое
потребление
(
fl
oat64)
b.
Среднедневное
потребление
(
fl
oat64)
c.
Среднее
потребление
по
дням
недели
(
fl
oat64)
d.
Средненедельное
потребление
(
fl
oat64)
e.
Среднемесячное
потребление
(
fl
oat64)
f.
Среднее
потребление
в
будни
/
выходные
(
fl
oat64)
g.
Лаги
(
fl
oat64)
Признаки
среднего
потребления
считаются
толь
-
ко
по
обучающей
выборке
.
Целевая
переменная
:
a.
Активное
потребление
(
fl
oat64)
Разбиение
на
выборки
происходит
следующим
образом
:
Временной
ряд
Обучающая
выборка
Прогнозный
период
Прогнозным
периодом
является
срез
общего
вре
-
менного
ряда
требуемой
длительности
(
день
,
не
-
деля
,
месяц
и
т
.
д
.),
всегда
берущийся
с
конца
вре
-
менного
ряда
,
так
как
случайное
перемешивание
значений
ряда
приводит
к
потере
временной
струк
-
туры
,
что
приводит
к
потере
всех
взаимосвязей
.
4.
Построение
прогнозных
моделей
Для
построения
прогнозных
моделей
воспользу
-
емся
библиотеками
sklearn, xgboost
и
statsmodels.
Bayesian Ridge
sklearn.linear_model.BayesianRidge(n_iter=300,
tol=0.001, alpha_1=1e-06, alpha_2=1e-06,
lambda_1=1e-06, lambda_2=1e-06, compute_
score=False, fit_intercept=True, normalize=False,
copy_X=True, verbose=False)
Elastic Net CV
sklearn.linear_model.ElasticNetCV(l1_ratio=0.5,
eps=0.001, n_alphas=100, alphas=None,
fit_intercept=True, normalize=False,
precompute=’auto’, max_iter=1000, tol=0.0001,
cv=None, copy_X=True, verbose=0, n_jobs=1,
positive=False, random_state=None,
selection=’cyclic’)
Huber Regressor
sklearn.linear_model.HuberRegressor(epsilon=1.35,
max_iter=100, alpha=0.0001, warm_start=False,
fit_intercept=True, tol=1e-05)
Linear Regression
sklearn.linear_model.LinearRegression(fit_intercept
=True, normalize=False, copy_X=True, n_jobs=1)
ЭНЕРГО-
ЭФФЕКТИВНОСТЬ
Рис
. 9.
Финальная
проверка
ряда
на
стационарность
51
Lasso Lars CV
sklearn.linear_model.LassoLarsCV(fit_intercept=True,
verbose=False, max_iter=500, normalize=True,
precompute=’auto’, cv=None, max_n_alphas=1000,
n_jobs=1, eps=2.2204460492503131e-16, copy_
X=True, positive=False)
Orthogonal Matching Pursuit CV
sklearn.linear_model.OrthogonalMatchingPursuitC
V(copy=True, fit_intercept=True, normalize=True,
max_iter=None, cv=None, n_jobs=1,
verbose=False)
Decision Tree Regressor
sklearn.tree.DecisionTreeRegressor(criterion=’m
se’, splitter=’best’, max_depth=None, min_
samples_split=2, min_samples_leaf=1, min_
weight_fraction_leaf=0.0, max_features=None,
random_state=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_
split=None, presort=False)
Extra Tree Regressor
sklearn.tree.ExtraTreeRegressor(criterion=’mse’,
splitter=’random’, max_depth=None, min_
samples_split=2, min_samples_leaf=1, min_
weight_fraction_leaf=0.0, max_features=’auto’,
random_state=None, min_impurity_
decrease=0.0, min_impurity_split=None, max_
leaf_nodes=None)
Random Forest Regressor
sklearn.ensemble.RandomForestRegressor(n_
estimators=10, criterion=’mse’, max_
depth=None, min_samples_split=2, min_
samples_leaf=1, min_weight_fraction_leaf=0.0,
max_features=’auto’, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_
split=None, bootstrap=True, oob_score=False,
n_jobs=1, random_state=None, verbose=0,
warm_start=False)
Табл
. 1.
Сравнение
суточных
прогнозов
Алгоритм
Суточный
прогноз
Реальное
потребле
-
ние
,
кВ
/
ч
Прогнозное
потребле
-
ние
,
кВ
/
ч
Погреш
-
ность
,
%
Скользящая
средняя
6999
6854
2,07
Взвешенное
среднее
6999
7254
3,64
Экспоненциальное
сглаживание
6999
7180
2,59
Bayesian Ridge
6999
7214
3,07
Elastic Net CV
6999
7215
3,09
Huber Regressor
6999
7032
0,47
Linear Regression
6999
7284
4,07
Lasso Lars CV
6999
7284
4,07
Orthogonal Matching
Pursuit CV
6999
7254
3,64
Decision Tree-
Regressor
6999
7119
1,71
Extra Tree Regressor
6999
7141
2,03
Random Forest-
Regressor
6999
7147
2,11
XGBRegressor 6999
7188
2,70
Табл
. 2.
Сравнение
недельных
прогнозов
Алгоритм
Недельный
прогноз
Реальное
потребле
-
ние
,
кВ
/
ч
Прогнозное
потребле
-
ние
,
кВ
/
ч
Погреш
-
ность
,
%
Модель
Хольта
-
Винтерса
50560
49742
1,62
SARIMA
50560
49550
2,00
Bayesian Ridge
50560
51814
2,48
Elastic Net CV
50560
51551
1,96
Huber Regressor
50560
51849
2,55
Linear Regression
50560
51915
2,68
Lasso Lars CV
50560
51253
1,37
Orthogonal Matching
Pursuit CV
50560
51804
2,46
Decision Tree-
Regressor
50560
52441
3,72
ExtraTreeRegressor
50560
51672
2,20
Random Forest-
Regressor
50560
52780
4,39
XGB Regressor
50560
51687
2,23
XGB Regressor
xgboost.XGBRegressor(max_depth=3, learning_
rate=0.1, n_estimators=100, silent=True,
objective='reg:linear', booster='gbtree', n_jobs=1,
nthread=None, gamma=0, min_child_weight=1,
max_delta_step=0, subsample=1, colsample_
bytree=1, colsample_bylevel=1, reg_alpha=0,
reg_lambda=1, scale_pos_weight=1, base_
score=0.5, random_state=0, seed=None,
missing=None, **kwargs)
SARIMA
statsmodels.tsa.statespace.sarimax.
SARIMAX(endog, exog=None, order=(1, 0,
0), seasonal_order=(0, 0, 0, 0), trend=None,
measurement_error=False, time_varying_
regression=False, mle_regression=True, simple_
differencing=False, enforce_stationarity=True,
enforce_invertibility=True, hamilton_
representation=False, **kwargs)[source]
Модели
,
основанные
на
методах
средних
и
экс
-
поненциального
сглаживания
,
реализованы
на
языке
Python 3
по
формулам
расчета
,
реализация
остается
на
усмотрение
исследователя
.
5.
Сравнение
результатов
прогноза
потребления
электроэнергии
,
полученных
с
использованием
различных
моделей
Построим
модели
на
основании
описанных
алго
-
ритмов
,
и
сравним
суточный
и
недельный
прогнозы
.
Метрикой
качества
выступает
MAPE (Mean Absolute
Percentage Error),
максимально
допустимое
значе
-
ние
— 3%.
1
N
|
Z
(
t
) –
Z
(
t
)|
MAPE = —
— · 100%.
N
t
= 0
Z
(
t
)
Результаты
представлены
в
таблицах
1
и
2.
№
2 (47) 2018

52
ЛИТЕРАТУРА
1.
Временные
ряды
,
составляющие
временного
ряда
. URL: https://
univer sity.prognoz.ru/biu/ru/.
2.
Льюис
К
.
Д
.
Методы
прогнозирова
-
ния
экономических
показателей
.
М
.:
Финансы
и
статистика
, 1986. 318
с
.
3.
Швец
Ю
.
А
.
Применение
метода
экспоненциального
сглаживания
для
краткосрочного
прогнозиро
-
вания
оборотных
средств
в
дея
-
тельности
предприятий
машино
-
строения
//
Основы
экономики
,
управления
и
права
, 2013,
№
5(11).
С
. 139–145.
4.
Открытый
курс
машинного
обуче
-
ния
.
Тема
9.
Анализ
временных
рядов
с
помощью
Python. URL:
https://habrahabr.ru/company/ods/
blog/327242/.
5.
Стационарность
временного
ряда
.
URL: https://university.prognoz.ru/biu/
ru/
Стационарность
_
временного
_
ряда
.
6.
Трегуб
А
.
В
.,
Трегуб
И
.
В
.
Методика
построения
модели
ARIMA
для
про
-
гнозирования
динамики
временных
рядов
//
Вестник
Московского
госу
-
дарственного
университета
леса
.
Лесной
вестник
,
Мытищи
, 2011,
№
5(81).
С
. 179–184.
7. Seasonal ARIMA with Python. URL:
http://www.seanabu.com/2016/03/22/
time-series-seasonal-ARIMA-model-
in-python/.
8.
Анализ
временных
рядов
с
помо
-
щью
Python. URL: https://habrahabr.
ru/post/207160/.
9.
Построение
модели
SARIMA
с
по
-
мощью
Python+R. URL: https://
habrahabr.ru/post/210530/.
10.
Рубашкин
Г
.
В
.
Прогнозирование
объ
-
емов
продаж
промышленных
пред
-
Сравнение
показывает
,
что
многие
модели
пока
-
зали
достаточный
результат
при
прогнозировании
—
погрешность
прогноза
не
превысила
допустимые
3%
(
в
таблицах
отмечены
зеленым
).
Однако
стоит
отме
-
тить
,
что
при
приблизительно
одинаковом
качестве
прогноза
есть
и
существенные
отличия
между
моде
-
лями
.
Так
,
модель
скользящей
средней
при
неодно
-
родной
структуре
потребления
будет
показывать
не
очень
стабильный
результат
,
так
как
она
недостаточно
быстро
адаптируются
к
резким
изменениям
значений
.
Это
же
справедливо
и
для
модели
взвешенной
сред
-
ней
.
При
этом
временные
затраты
на
их
подготовку
ни
-
чтожны
,
и
они
не
требуют
большого
объема
данных
.
Фактически
,
прогноз
с
использованием
модели
про
-
стых
средних
можно
строить
,
имея
15–20
наблюдений
.
Модели
экспоненциального
и
двойного
экспонен
-
циального
сглаживания
покажут
на
неоднородных
данных
более
стабильный
результат
,
но
при
этом
временные
затраты
(
подбор
оптимальных
коэффи
-
циентов
)
возрастают
.
Количество
данных
,
необходи
-
мых
для
построения
прогноза
по
подобным
моделям
,
зависит
от
значения
коэффициентов
и
,
как
в
случае
моделей
простых
средних
,
потребует
не
более
ста
на
-
блюдений
,
так
как
при
большем
количестве
учитывае
-
мых
данных
прогноз
будет
сильно
усреднен
,
начиная
представлять
из
себя
среднее
по
времени
.
SARIMA
и
модель
Хольта
-
Винтерса
требует
значи
-
тельно
больших
временных
затрат
на
предобработку
данных
,
подбор
параметров
,
обучение
и
переобуче
-
ние
модели
.
Однако
при
качественно
проведенной
подготовке
модели
на
длительных
периодах
прогноза
SARIMA
будет
более
стабильна
,
нежели
модель
Холь
-
та
-
Винтерса
или
модели
,
построенные
при
помощи
алгоритмов
машинного
обучения
.
При
этом
для
каче
-
ственной
модели
SARIMA
необходимы
данные
о
по
-
треблении
за
4–5
сезонов
,
учитывая
что
сезон
может
описываться
как
кварталом
,
так
и
годом
.
Модели
,
построенные
на
основе
регрессионных
алгоритмов
,
также
неоднородны
по
временным
за
-
тратам
на
их
подготовку
.
Простая
линейная
регрессия
требует
времени
на
подготовку
в
разы
меньше
,
чем
модель
XGB Regressor,
и
на
порядок
меньше
,
чем
SARIMA,
показывая
при
этом
схожие
результаты
,
но
требуют
большего
количества
данных
для
качествен
-
ного
обучения
модели
,
чем
при
подготовке
модели
на
базе
SARIMA.
При
этом
в
случае
с
регрессионными
моделями
сезонность
не
имеет
значения
,
и
компен
-
сировать
недостаток
данных
можно
использованием
бустинга
.
Стоить
отметить
,
что
на
данный
момент
времен
-
ные
затраты
непосредственно
на
само
обучение
мо
-
дели
,
без
учета
времени
на
подготовку
данных
,
мож
-
но
снизить
,
используя
современные
вычислительные
комплексы
,
однако
есть
ряд
факторов
,
которые
сто
-
ит
принять
во
внимание
.
Первый
фактор
сопряжен
с
прямыми
затратами
на
модернизацию
существующих
вычислительных
средств
либо
на
их
аренду
,
дополни
-
тельное
обучение
или
привлечение
соответствующих
специалистов
.
Второй
же
фактор
связан
с
тем
,
что
не
каждая
модель
позволяет
производить
параллельные
вычисления
при
своем
обучении
,
а
выгода
от
роста
производительности
при
последовательном
вычисле
-
нии
на
более
мощном
оборудовании
может
не
покры
-
вать
капитальных
затрат
на
модернизацию
.
ВЫВОДЫ
В
ходе
работ
было
исследовано
потребление
элек
-
троэнергии
на
собственные
нужды
ПС
500
кВ
«
Челя
-
бинская
»
ПАО
«
ФСК
ЕЭС
».
Исследование
показало
,
что
структура
потребления
представляет
собой
вре
-
менной
ряд
с
четким
трендом
и
сезонностью
интерва
-
лом
в
1
год
,
совпадающим
с
естественным
годовым
циклом
смены
времен
года
.
Проведенный
обзор
показал
наличие
широкого
ар
-
сенала
имеющихся
алгоритмов
для
прогнозирования
временных
рядов
,
их
активное
применение
для
реше
-
ния
практических
задач
.
На
практике
были
показаны
различные
способы
подготовки
данных
для
моделей
машинного
обуче
-
ния
,
отличия
при
подготовке
данных
для
моделей
,
где
в
качестве
признаков
используются
значения
про
-
шлых
периодов
и
моделей
,
использующих
в
качестве
признаков
синтетические
переменные
,
такие
как
ка
-
лендарные
признаки
.
Были
подготовлены
прогнозные
модели
на
основе
отобранных
алгоритмов
,
составлены
суточный
и
не
-
дельный
прогнозы
,
проведено
сравнение
результатов
работы
различных
моделей
.
Таким
образом
,
выбор
модели
зависит
от
структу
-
ры
данных
,
требований
к
точности
прогноза
,
времен
-
ных
ресурсов
,
квалификации
персонала
,
а
широкий
арсенал
современных
алгоритмов
позволяет
подо
-
брать
нужный
инструментарий
,
исходя
из
имеющихся
возможностей
и
поставленных
задач
.
ЭНЕРГО-
ЭФФЕКТИВНОСТЬ

53
приятий
на
основе
моделей
мно
-
жественной
линейной
регрессии
//
Экоомический
анализ
, 2006,
№
8.
11.
Воронцов
К
.
И
.
Нелинейная
регрес
-
сия
.
Обобщенные
линейные
моде
-
ли
.
Нестандартные
функции
потерь
.
URL: http://www.machinelearning.ru/
wiki/images/4/43/Voron-ML-regress-
non-slides.pdf.
12. Cosma Shalizi. Classi
fi
cation and Re-
gres sion Trees. URL: http://www.stat.
cmu.edu/~cshalizi/350/lectures/22/
lecture-22.pdf.
13.
Китов
В
.
В
.
Исследование
точности
метода
градиентного
бустинга
со
случайными
поворотами
//
Статисти
-
ка
и
экономика
, 2016,
№
4.
С
. 22–26.
14.
Канторович
Г
.
Г
.
Анализ
временных
рядов
//
Экономический
журнал
ВШЭ
, 2003,
№
1.
С
. 85–103.
REFERENCES
1.
Vremennye ryady, sostavlyayushchie
vremennogo ryada
(Time series
and their components). Available at:
https://university.prognoz.ru/biu/ru/
(accessed April 01, 2018).
2. Lyuis K.D.
Metody prognozirovaniya
ekonomicheskikh pokazateley
[Me-
thods of economic indicators fore-
casting]. Moscow, Finansy i statistika
Publ., 1986. 318 p.
3. Shvets Yu.A. Application of exponen-
tial smoothing method for short-term
forecasting of machine-building plant
current assets.
Osnovy ekonomiki,
upravleniya i prava
[Fundamentals of
Economics, Management and Law],
2013, no. 5(11), pp. 139-145. (in Rus-
sian)
4.
Otkrytyy kurs mashinnogo obucheni-
ya. Tema 9. Analiz vremennykh rya-
dov s pomoshchyu Python
(Open
machine learning course. Theme 9.
Analysis of time series by means of
Python). Available at: https://habra-
habr.ru/company/ods/blog/327242/
(accessed April 01, 2018).
5.
Statsionarnost vremennogo ryada
(Time series stationarity). Available
at: https://university.prognoz.ru/biu/ru/
Стационарность
_
временного
_
ряда
(accessed April 01, 2018).
6. Tregub A.V., Tregub I.V. The method
of ARIMA model construction for pre-
dicting the dynamics of time series.
Vestnik Moskovskogo gosudarstven-
nogo universiteta lesa. Lesnoi vestnik
[Bulletin of the Moscow State Forest
University. Forest Herald], 2011, no.
5(81), pp. 179-184. (in Russian)
7. Seasonal ARIMA with Python. Avail
-
able at: http://www.seanabu.com/
2016/03/22/time-series-seasonal-
ARIMA-model-in-python/ (accessed
April 01, 2018).
8. Analiz vremennykh ryadov s pomosh-
chyu Python (Time series analysis
with Python). Available at: https://
habrahabr.ru/post/207160/ (accessed
April 01, 2018).
9. Postroenie modeli SARIMA s po-
moshchyu Python+R (Building SARI-
MA model with Python + R). Available
at: https://habrahabr.ru/post/207160/
(accessed April 01, 2018).
10. Rubashkin G.V. Forecasting the vol-
ume of industrial enterprises sales on
the basis of multiple linear regression
models. Ekonomicheskiy analiz [Eco-
nomic analysis], 2006, no. 8. (in Rus-
sian)
11. Vorontsov K.I. Nelineynaya regres-
siya. Obobshchennye lineynye mod-
eli. Nestandartnye funktsii poter (Non-
linear regression. Generalized linear
models. Nonstandard loss functions).
Available at: http://www.machine-
learning.ru/wiki/images/4/43/Voron-
ML-regress-non-slides.pdf (accessed
April 01, 2018).
12. Cosma Shalizi. Classi
fi
cation and Re-
gression Trees. Available at: http://
www.stat.cmu.edu/~cshalizi/350/
lectures/22/lecture-22.pdf (accessed
April 01, 2018).
13. Kitov V.V. Investigation of accuracy
for gradient boosting method with
random turns. Statistika i ekonomika
[Statistics and Economics], 2016,
no. 4, pp. 22-26. (in Russian)
14. Kantorovich G.G. Time series analy-
sis. Ekonomicheskiy zhurnal VShE
[Economic Journal of the Higher
School of Economics], 2003, no. 1,
pp. 85-103. (in Russian)
тел/факс: +7 (351)211-54-01
e-mail: info@limi.ru
Internet: www.limi.ru
џ
Измерение переходных сопротивлений током до 200 А
џ
Измерение сопротивления главных контактов высоковольтных выключателей
џ
Питание от встроенных аккумуляторов
џ
Диапазон измерения электрического сопротивления от 1 мкОм до 0,1 Ом
џ
Измерение сопротивления обмоток трансформаторов большой мощности
џ
Существенно меньшее, по сравнению с имеющимися аналогами, время
измерения сопротивления высокоиндуктивных цепей
џ
Широкий диапазон измерений сопротивления: от 1 мкОм до 2000 Ом
ОТЕЧЕСТВЕННЫЙ ПРОИЗВОДИТЕЛЬ ПРИБОРОВ ДЛЯ ДИАГНОСТИКИ В ЭНЕРГЕТИКЕ
Подробная информация на сайте
www.limi.ru
џ
Измерение сопротивления контактов
џ
Измерение сопротивления обмоток трансформаторов до 1000 кВА
џ
Оптимальное решение для мобильных бригад, обслуживающих сети 6/10 кВ
џ
Диапазон измерения электрического сопротивления от 1 мкОм до 200 Ом
Микромиллиомметр ИКС-1А «Энергетик»
Микроомметр ИКС-200А
Миллиомметр ТРОМ-1
РЕШЕНИЕ ВОПРОСА ИЗМЕРЕНИЯ НИЗКОГО
ЭЛЕКТРИЧЕСКОГО СОПРОТИВЛЕНИЯ В ЭНЕРГЕТИКЕ
На
правах
рекламы
№
2 (47) 2018
Оригинал статьи: Прогнозирование потребления электроэнергии. Практика применения
Современные тенденции развития рынка электроэнергетики в Российской Федерации характеризуются постоянным ростом цен на ресурсы, которые необходимы топливно-энергетическому комплексу для непрерывного производства электроэнергии, удорожанием процесса возведения новых электростанций и энергосетей для транспортировки энергии и повсеместным ростом неплатежеспособности предприятий-потребителей электроэнергии. Реформирование РАО «ЕЭС России» в 2008 году привело всех участников образовавшегося оптового рынка электроэнергии и мощности к необходимости вырабатывать свои уникальные стратегии и инструменты использования энергоресурсов с целью обеспечения баланса между вырабатываемой и потребляемой энергией. В данной статье производится сравнение различных способов прогнозирования потребления электроэнергии с использованием алгоритмов машинного обучения и статистических методов на примере прогноза потребления электроэнергии на собственные нужды ПС 500 кВ «Челябинская» ПАО «ФСК ЕЭС».