«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
38
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß
О
сновной задачей импульсных измерений
является определение расстояния до по-
вреждения или неоднородности по зареги-
стрированной рефлектограмме [1, 2]. Од-
нако на практике результаты измерений по рефлек-
тограмме часто имеют большую погрешность. Дан-
ная работа посвящена повышению точности измере-
ния расстояний рефлектометрическими цифровыми
приборами.
Под рефлектограммой мы понимаем зависи-
мость напряжения сигнала обратного потока от вре-
мени задержки (расстояния). Рефлектограмма, по-
лученная с помощью современного цифрового реф-
лектометра, представляет собой совокупность от-
счётов напряжения сигнала обратного потока
u
2i
в
моменты времени
t
i
, интервал
t
между которыми
определяется частотой дискретизации
f
d
=1/
t
. От-
счёт времени
t
i
ведётся от начала зондирующего им-
пульса.
Между временем
t
i
и расстоянием
l
i
на рефлекто-
грамме существует соотношение:
, (1)
где
z
— удельное время задержки линии (с/км)
[2, 3]. Тогда расстояние
l
между соседними отсче-
тами
l
i
на рефлектограмме составит
.
Обратным потоком называют совокупность отра-
жённых от неоднородностей сигналов. Принято раз-
личать: концевые, стыковые и внутренние неодно-
родности [1, 2]. Можно также говорить о резистив-
ных, ёмкостных, индуктивных и комплексных неод-
нородностях, которые могут включаться в линию па-
раллельно и последовательно. На практике чаще
всего встречаются резистивные и стыковые неодно-
родности. Их особенностью является то, что их им-
пульсная характеристика соответствует по форме
импульсной характеристике линии
g(t)
с длиной, рав-
ной удвоенному расстоянию до неоднородности
2l
n
:
, при t
t
z
, (2)
где
t
z
= 2
z
•
l
n
— время задержки выходного импуль-
са относительно зондирующего (с),
o
— удель-
ная конструктивная постоянная кабельной цепи
(с/км
2
). Значения параметров
o
и
z
для различных
кабельных цепей приведены в [3].
Для расчёта формы отражённого от единствен-
ной неоднородности импульса на входе рефлекто-
метра
u
r
(t)
без учёта шумов и помех можно исполь-
зовать выражение:
(3)
где
u
1
(t)
— форма зондирующего импульса, r — ко-
эффициент отражения от неоднородности.
В литературе [4, 5] рекомендуется определять
расстояние по началу переднего фронта отражённо-
го от неоднородности импульса.
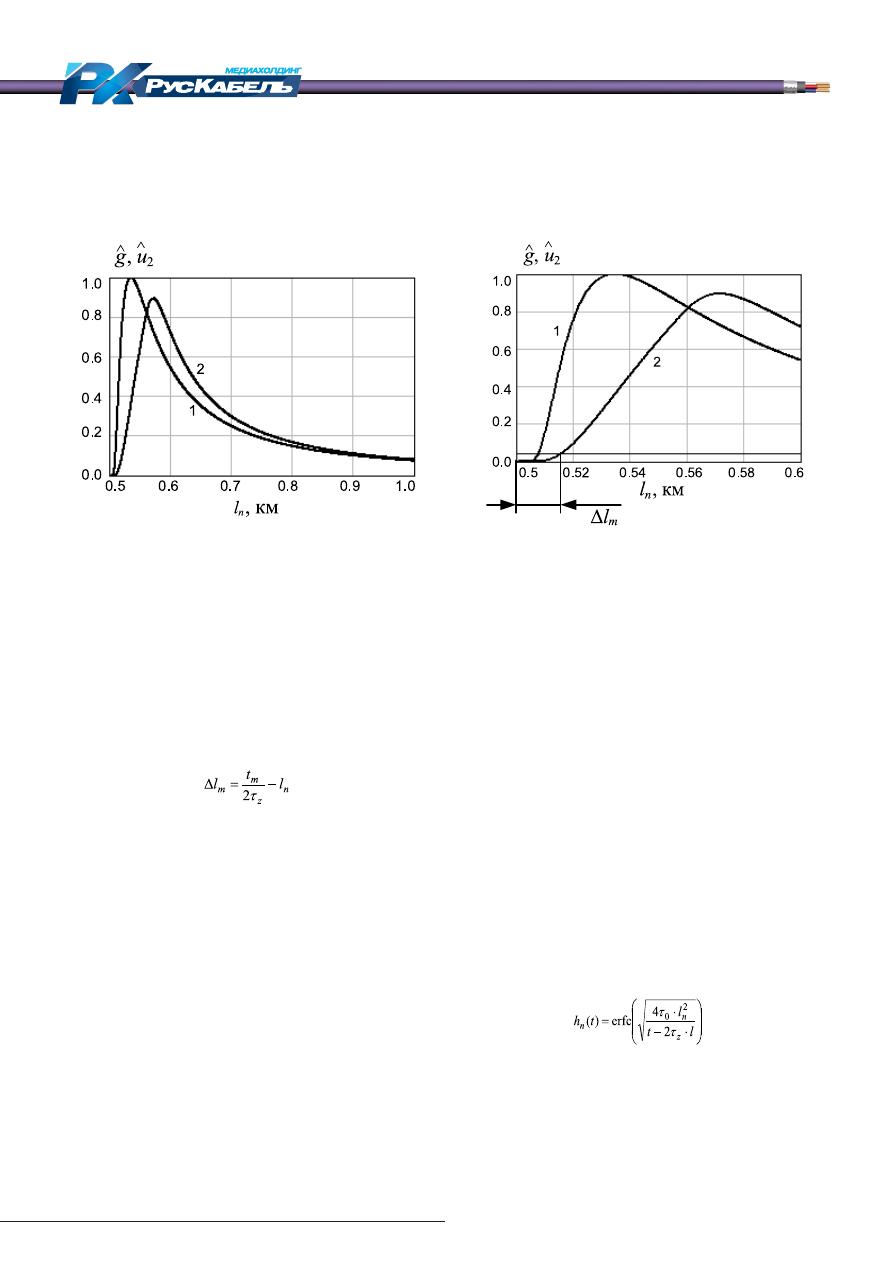
На рис. 1 а показаны нормализованные импульс-
ная характеристика резистивной неоднородности и
форма отражённого от нее импульса. Расчёт произ-
ведён для кабеля ТПП-0,4,
l
n
= 0,5 км,
o
= 497,4 нс/км
2
,
z
= 4,8 мкс/км и прямоугольного зондирующего им-
пульса длительностью 500 нс. На рис. 1 б показа-
Повышение точности
определения расстояний
по рефлектограммам
кабельных цепей
Мария БЫЛИНА, к.т.н., доцент кафедры «Линии связи»,
Сергей ГЛАГОЛЕВ, к.т.н., профессор кафедры «Линии связи»,
Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М.А. Бонч-Бруевича
«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
39
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß
ны те же зависимости на начальном участке. Видно,
что скорость нарастания переднего фронта импульс-
ной характеристики и отражённого импульса снача-
ла невелика. Поэтому начало переднего фронта им-
пульса трудно обнаружить.
Будем считать, что измеритель локализует неод-
нородность в точке, где величина отражённого им-
пульса составляет не менее
m•U
2m
, где
U
2m
— ампли-
туда отражённого импульса,
m
<1. На рис. 1 б пока-
зано, что в этом случае возникает погрешность ло-
кализации неоднородности
l
m
:
(4
а)
или в единицах времени:
t
m
= t
m
– 2
z
l
n
(4
б)
где
t
m
— момент времени, в который передний фронт
отражённого импульса пересекает уровень
m•U
2m
:
u
2
(t
m
) = m•U
2m
(5)
Уравнение (5) не имеет аналитического решения,
но может быть решено численным методом.
Отметим, что погрешность локализации
l
m
(
t
m
)
зависит от конструктивной постоянной кабельной
цепи
o
, расстояния до неоднородности
l
n
, формы
u
1
(t)
и длительности
t
p
зондирующего импульса.
Таким образом, локализация с высокой точно-
стью начала отражённого импульса, особенно в при-
сутствии шумов и при наличии предшествующих от-
ражений, является сложной задачей.
Известно, что при длительности униполярного
зондирующего импульса, намного меньшей постоян-
ной времени по отражению
4
o
l
2
n
, отражённый от не-
однородности импульс принимает форму импульс-
ной характеристики
g
n
(t)
(2):
u
2g
(t) = S
p
•g
n
(t)
, (6)
где
S
p
— площадь зондирующего импульса. Ампли-
туда отражённого импульса будет равна:
U
2mg
= S
p
•G
nm
,
(7)
где
G
nm
— амплитуда импульсной характеристики.
Таким образом, минимально достижимая по-
грешность локализации неоднородности, находя-
щейся на расстоянии
l
n
от начала линии, при исполь-
зовании традиционной методики составит:
в единицах времени:
t
min
= t
mg
– 2
z
l
n
,
в единицах расстояния:
l
min
= (t
mg
/2
z
) – l
n
,
где
t
mg
— момент времени, в который передний фронт
отражённого импульса пересекает уровень
m
•
U
2
mg
:
u
2g
(t
mg
) = m•U
2mg
, (9)
Уравнение (9) не имеет аналитического решения,
но может быть решено численным методом.
Отметим, что с увеличением длительности зон-
дирующего импульса погрешность локализации не-
однородности будет возрастать. Максимальное зна-
чение погрешности будет достигнуто при исполь-
зовании в качестве зондирующего импульса сту-
пенчатого перепада напряжения:
u
1
(t) = U
1
•1(t)
,
где
1(t)
— функция Хэвисайда. Известно, что при
распространении по кабельной цепи такой импульс
принимает форму её переходной характеристики,
которая для отражения от неоднородности, находя-
щейся на расстоянии ln от начала линии, имеет вид:
(10)
Для формы отражённого импульса будет спра-
ведливо:
u
2h
(t) = U
1
•h
n
(t),
(11)
Таким образом, максимальная погрешность ло-
кализации неоднородности, находящейся на рассто-
янии
l
n
от начала линии, при использовании традици-
онной методики составит:
в единицах времени:
t
max
= t
mh
– 2
z
l
n
,
в единицах расстояния:
l
max
= (t
mh
/2
z
) – l
n
,
(8)
(12)
Рис. 1. Нормализованные импульсная характеристика резистивной неоднородности (1)
и форма отражённого от неё импульса (2)
a
б
«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
40
где
t
mh
— момент времени, в который передний фронт
отражённого импульса пересекает уровень
m
•
U
1
:
u
2h
(t
mh
) = m•U
1
.
(13)
Уравнение (13) не имеет аналитического реше-
ния, но может быть решено численным методом.
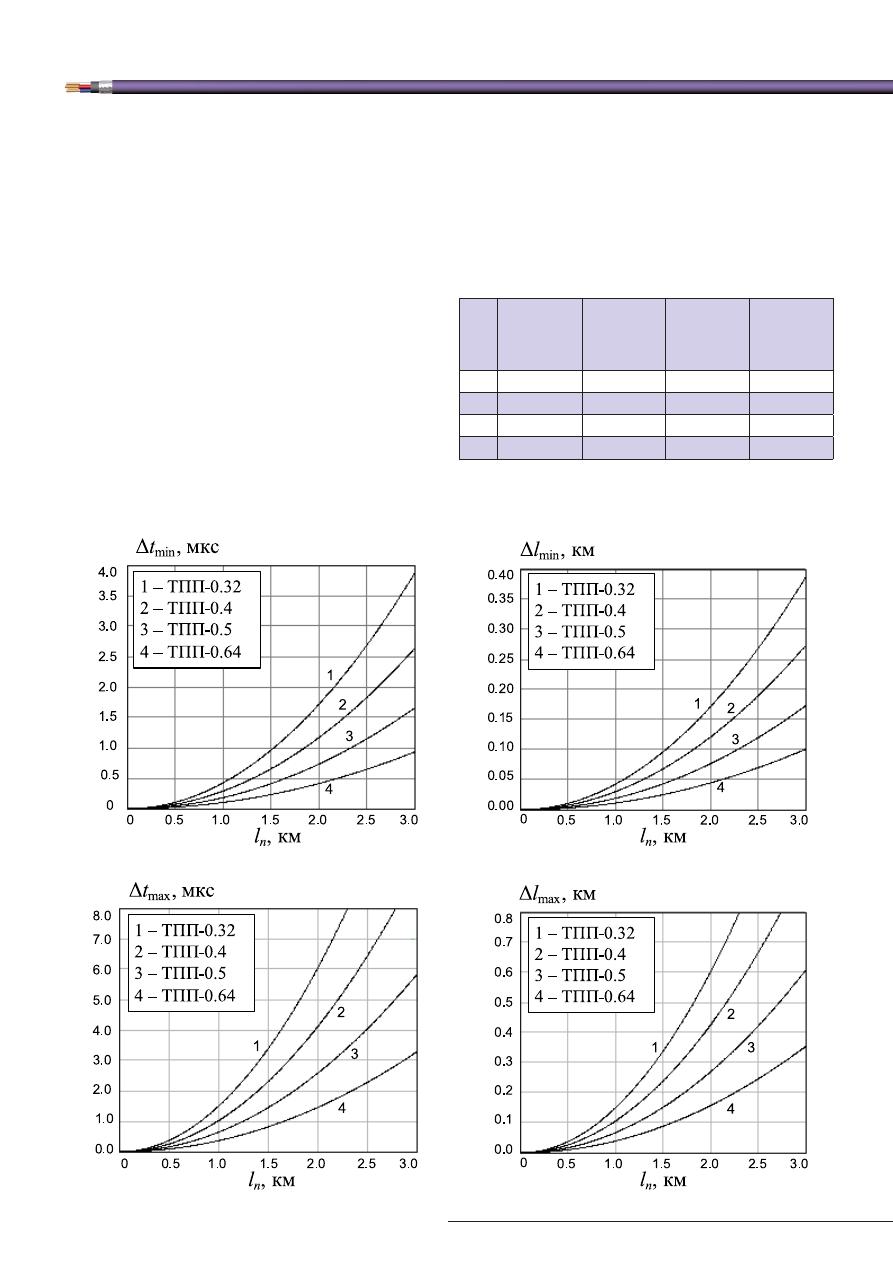
На рис. 2 показаны зависимости минимальных
t
min
и
l
min
и максимальных
t
max
и
l
max
погрешностей
локализации неоднородности от расстояния до неё
для кабельных цепей ТПП с различным диаметром
жил. Расчёты проведены при
m
=0,05. Видно, что по-
грешность возрастает с увеличением конструктив-
ной постоянной кабельной цепи (уменьшением диа-
метра жил) и расстояния до неоднородности.
Авторами было обнаружено, что величины
t
min
(l
n
,m)=
t
min
( l
n
,m)/
o
и
t
max
(l
n
,m)=
t
max
( l
n
,m)/
o
зави-
сят только от расстояния до неоднородности и уров-
ня
m
и не зависят от типа кабельной цепи. На рис. 3
приведены зависимости
t
min
(l
n
,m)
и
t
max
(l
n
,m)
от рас-
стояния до неоднородности.
Таблица 1
m
A
mg
Погрешность
аппрок
-
симации
t
min
(l
n
,m)
,
%
A
mh
Погреш
-
ность
ап
-
проксимации
t
max
(l
n
,m)
,
%
0,01
0,45710990
0,98•10
-5
1,20563077
1,43•10
-6
0,03 0,54048743
1,08•10
-5
1,69877060
7,90•10
-7
0,05 0,59238403
1,53•10
-5
2,08256165
1,77•10
-6
0,07 0,63335279
0,99•10
-5
2,43674459
6,35•10
-5
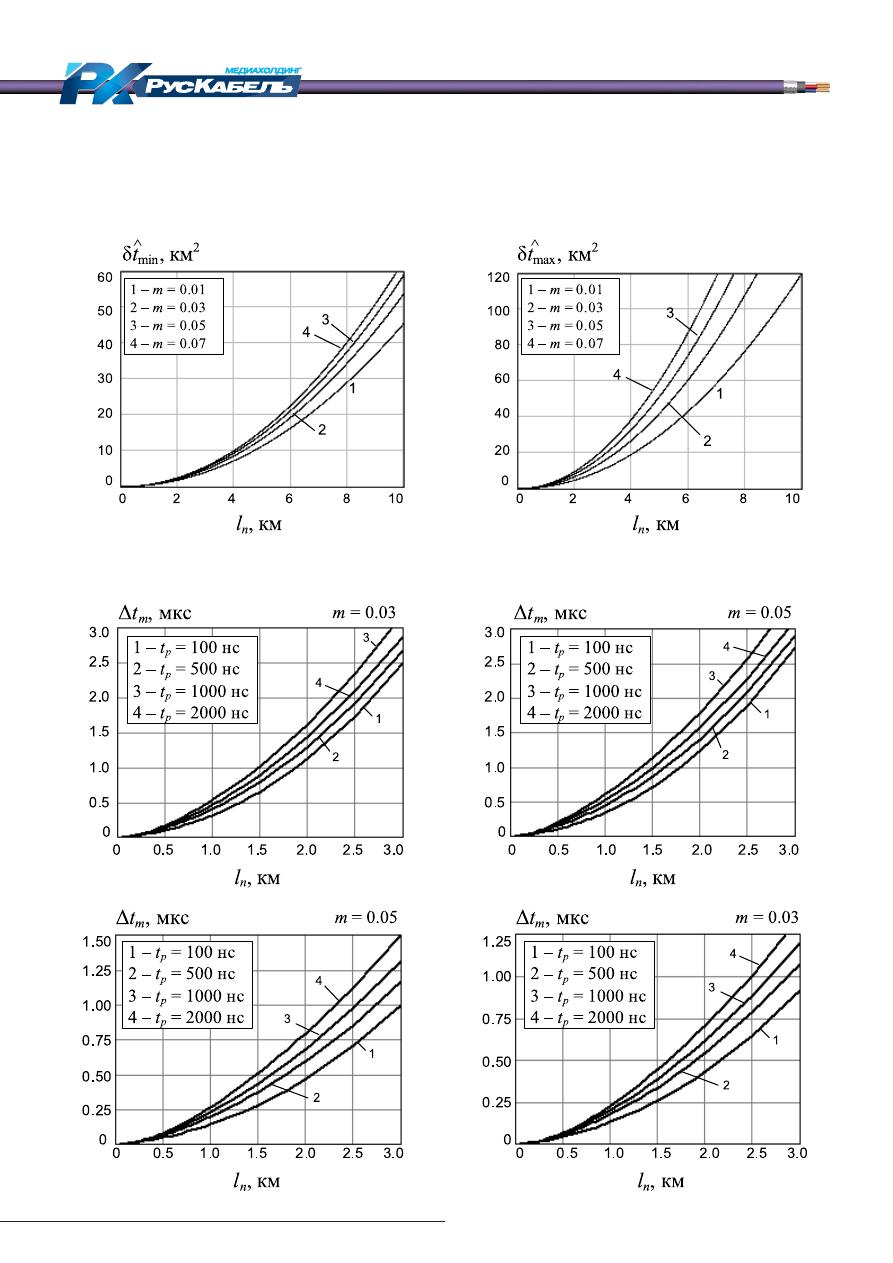
Рис. 2. Зависимости минимальных (а и б) и максимальных (в и г) погрешностей
определения расстояния до неоднородности
a
в
г
б
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß
«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
41
Рис. 3. Зависимости минимальных (а) и максимальных (б) нормированных погрешностей
от расстояния до неоднородности
a
б
Рис. 4. Зависимости погрешностей от расстояния до неоднородности, рассчитанные
для кабельных цепей ТПП-0,4 (а, б) и ТПП-0,64 (в, г)
a
б
в
г
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß
«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
42
Представленные на рис. 3 кривые хорошо ап-
проксимируются функциями вида
t
min
(l
n
,m) = A
mg
•l
2
n
,
t
max
(l
n
,m) = A
mh
•l
2
n
(14)
где
A
mg
и
A
mh
— представленные в табл. 1 коэф-
фициенты аппроксимации, полученные для разных
значений
m
.
На рис. 4 представлены зависимости величины
t
m
от расстояния до неоднородности, рассчитанные
для различных длительностей прямоугольных зон-
дирующих импульсов и различных уровней
m
.
Из рис. 4 видно, что при использовании традици-
онного способа определения расстояния до неодно-
родности возникает значительная методическая си-
стематическая погрешность, зависящая как от рас-
стояния до неоднородности, так и от длительности
зондирующего импульса.
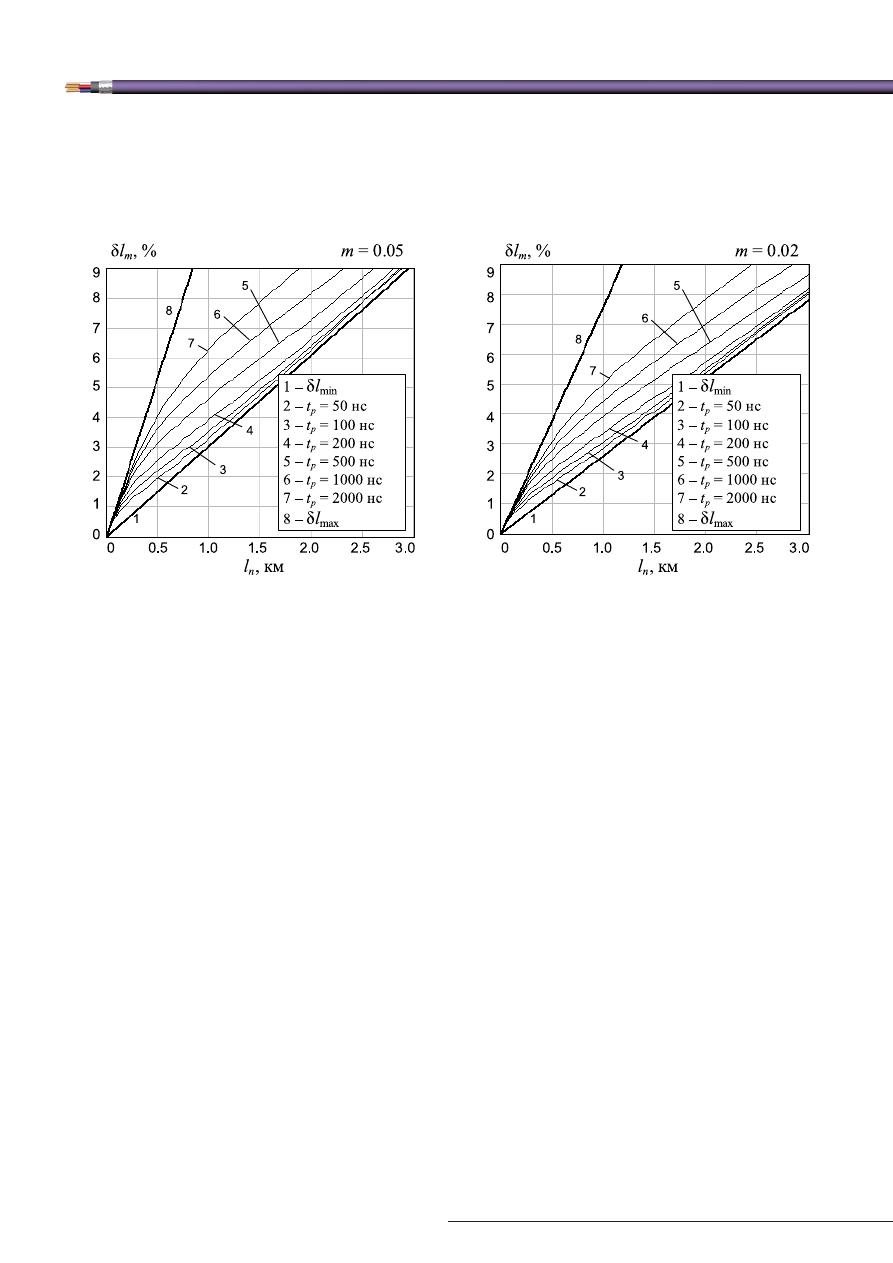
На рис. 5 показаны зависимости относительной
погрешности
l
m
локализации неоднородности от
расстояния до неё для кабельных цепей ТПП-0,4 при
различных длительностях прямоугольных зондиру-
ющих импульсов и двух значениях
m
. Для сравне-
ния на рис. 5 приведены также аналогичные зави-
симости для минимальной и максимальной погреш-
ностей.
Видно, что хотя погрешность и возрастает с уве-
личением длительности зондирующего импульса, с
увеличением расстояния до неоднородности вклад,
связанный с определённой длительностью зондиру-
ющего импульса, уменьшается и погрешность при-
ближается к
l
min
.
Из рис. 5 также видно, что снижение уровня
m
ведёт к уменьшению погрешности локализации не-
однородности. Однако значение
m
нельзя выбирать
ниже некоторого минимального уровня, определя-
емого случайными колебаниями волнового сопро-
тивления за счёт внутренних неоднородностей. Ко-
личественные характеристики внутренних неодно-
родностей кабельных цепей подробно рассмотре-
ны в [6].
Известно, что результат измерения расстояния
до неоднородности зависит от установленного при
регистрации или анализе рефлектограммы коэффи-
циента укорочения, который традиционно считается
параметром кабельной цепи:
K
yk
= c/v,
(15
а)
где
c
— скорость света в вакууме,
v
— скорость рас-
пространения электромагнитного импульса по дан-
ной цепи. Коэффициент укорочения связан с удель-
ным временем задержки
z
соотношением:
K
yk
= c •
z
,
(15
б)
Скорость распространения монохроматической
электромагнитной волны по кабельной цепи зави-
сит не только от параметров самой цепи, но и от
частоты, а значит,
v
и
K
yk
будут зависеть от фор-
мы и длительности зондирующего импульса. Кро-
ме того, в результате искажения зондирующего им-
пульса, распространяющегося по кабельной цепи,
его спектр изменяется, в нём начинают преобла-
дать низкочастотные составляющие, имеющие
меньшую скорость, что приводит к возрастанию
K
yk
.
Таким образом, коэффициент укорочения не явля-
ется постоянной величиной, а зависит от расстоя-
ния до неоднородности и параметров зондирующе-
го импульса.
Рис. 5. Влияние длительности импульса на относительную погрешность определения
расстояния до неоднородности
a
б
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß

«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
43
Для повышения точности определения расстоя-
ния рекомендуется экспериментально определить
удельное время задержки по зарегистрированной
рефлектограмме разомкнутой или короткозамкну-
той кабельной цепи известной длины
l
n
. Для этого
необходимо следующее.
1. Перейти от отсчётов расстояния
l
i
к отсчётам
времени
t
i
:
(16)
где
K
yk0
— коэффициент укорочения, при котором ре-
гистрировалась рефлектограмма.
2. Определить
t
m
— положение переднего фрон-
та импульса, отражённого от обрыва или короткого
замыкания, на уровне
mU
r
, где
U
r
— амплитуда отра-
жённого импульса.
3. Расcчитать теоретическое значение
t
m
для ка-
бельной цепи длиной
l
n
.
4. Опредить
t
f
— момент начала импульса, отра-
жённого от обрыва или короткого замыкания:
t
f
= t
m
–
t
m
. (17)
5. Определить
z izm
:
z izm
= t
f
/ 2l
n
. (18)
6. Для проведения дальнейших измерений уста-
новить коэффициент укорочения в импульсном при-
боре равным:
K
yk izm
= c •
z izm
, (19)
Величины
t
m
и
t
m
, как было показано выше, за-
висят от выбранного значения m, расстояния до не-
однородности
l
n
, а также формы и длительности зон-
дирующего импульса. Поэтому использование
K
yk izm
для измерения расстояний до неоднородностей, су-
щественно отличающихся от калибровочной дли-
ны, приводит к систематической погрешности изме-
рения, которая также будет зависеть от параметров
зондирующего импульса.
Следует отметить, что получение
t
m
для опре-
делённого значения
l
n
является трудоёмкой про-
цедурой, включающей расчёт импульсной харак-
теристики отражения от неоднородности, находя-
щейся на расстоянии
l
n
, и свёртку импульсной ха-
рактеристики с зондирующим импульсом для по-
лучения отражённого импульса. Для снижения тру-
доёмкости необходимо аппроксимировать величи-
ну
t
m
некоторой функцией, зависящей от
0
, l
n
, t
p
,
m
, а также от формы зондирующего импуль-
са. Для прямоугольного зондирующего импульса
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß

«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
44
l
n
,
м
t
p
,
нс
m
До
уточнения
результатов
измерений
После
уточнения
результатов
измерений
Измеренное
расстояние
,
м
Абсолютная
по
-
грешность
,
м
Относительная
погрешность
, %
Уточнённое
расстояние
,
м
Абсолютная
по
-
грешность
,
м
Относительная
погрешность
, %
254,65
62,5
0,03
258,36
3,71
1,46
254,42
-0,22
-0,09
0,05
258,57
3,92
1,54
254,65
0,00
0,00
0,07
258,99
4,34
1,71
255,07
0,42
0,17
125
0,03
258,78
4,13
1,62
254,20
-0,44
-0,17
0,05
259,21
4,56
1,79
254,69
0,04
0,02
0,07
259,63
4,98
1,96
255,15
0,50
0,20
250
0,03
259,21
4,56
1,79
253,88
-0,77
-0,30
0,05
260,06
5,41
2,12
254,82
0,17
0,07
0,07
260,48
5,83
2,29
255,31
0,66
0,26
375
0,03
259,21
4,56
1,79
253,41
-1,24
-0,49
0,05
260,06
5,41
2,12
254,37
-0,28
-0,11
0,07
260,48
5,83
2,29
254,88
0,23
0,09
500
0,03
258,78
4,13
1,62
252,67
-1,98
-0,78
0,05
259,63
4,98
1,96
253,64
-1,01
-0,40
0,07
260,48
5,83
2,29
254,57
-0,08
-0,03
625
0,03
259,21
4,56
1,79
252,82
-1,83
-0,72
0,05
260,06
5,41
2,12
253,79
-0,86
-0,34
0,07
260,48
5,83
2,29
254,32
-0,33
-0,13
502,5
62,5
0,03
513,95
11,45
2,28
501,84
-0,66
-0,13
0,05
515,01
12,51
2,49
502,68
0,18
0,04
0,07
515,44
12,94
2,57
502,91
0,41
0,08
125
0,03
511,61
9,11
1,81
497,98
-4,52
-0,90
0,05
515,01
12,51
2,49
501,21
-1,29
-0,26
0,07
516,71
14,21
2,83
502,77
0,27
0,05
250
0,03
516,71
14,21
2,83
502,78
-1,72
-0,34
0,05
518,41
15,91
3,17
502,56
0,06
0,01
0,07
519,26
16,76
3,33
503,44
0,94
0,19
375
0,03
517,14
14,64
2,91
499,77
-2,73
-0,54
0,05
518,84
16,34
3,25
501,65
-0,85
-0,17
0,07
520,11
17,61
3,50
503,02
0,52
0,10
500
0,03
517,99
15,49
3,08
499,48
-3,02
0,60
0,05
519,69
17,19
3,42
501,43
-1,07
-0,21
0,07
521,39
18,89
3,76
503,26
0,76
0,15
625
0,03
516,71
14,21
2,83
497,39
-5,11
-1,02
0,05
519,26
16,76
3,34
500,20
-2,30
-0,46
0,07
520,96
18,46
3,67
502,07
-0,43
-0,09
758,5
62,5
0,03
789,52
31,02
4,09
764,69
6,19
0,82
0,05
789,52
31,02
4,09
763,98
5,48
0,72
0,07
789,52
31,02
4,09
763,36
4,86
0,64
125
0,03
786,12
27,62
3,64
758,73
0,23
0,03
0,05
787,82
29,32
3,86
759,93
1,43
0,19
0,07
787,82
29,32
3,86
759,53
1,03
0,14
250
0,03
789,52
31,02
4,09
758,35
-0,14
-0,02
0,05
792,07
33,57
4,42
760,70
2,20
0,29
0,07
792,92
34,42
4,54
761,36
2,86
0,38
375
0,03
790,37
31,87
4,20
756,62
-1,88
-0,25
0,05
792,92
34,42
4,54
759,19
0,69
0,09
0,07
794,61
36,11
4,76
760,82
2,32
0,31
500
0,03
792,91
34,41
4,54
756,99
-1,51
-0,20
0,05
794,61
36,11
4,76
758,95
0,44
0,06
0,07
797,16
38,66
5,10
761,49
2,99
0,39
625
0,03
790,37
31,87
4,20
752,95
-5,55
-0,73
0,05
794,61
36,11
4,76
757,41
-1,09
-0,14
0,07
796,31
37,81
4,98
759,27
0,77
0,10
Таблица 2
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß
«КАБЕЛЬ-news», № 5, 2011, www.kabel-news.ru
45
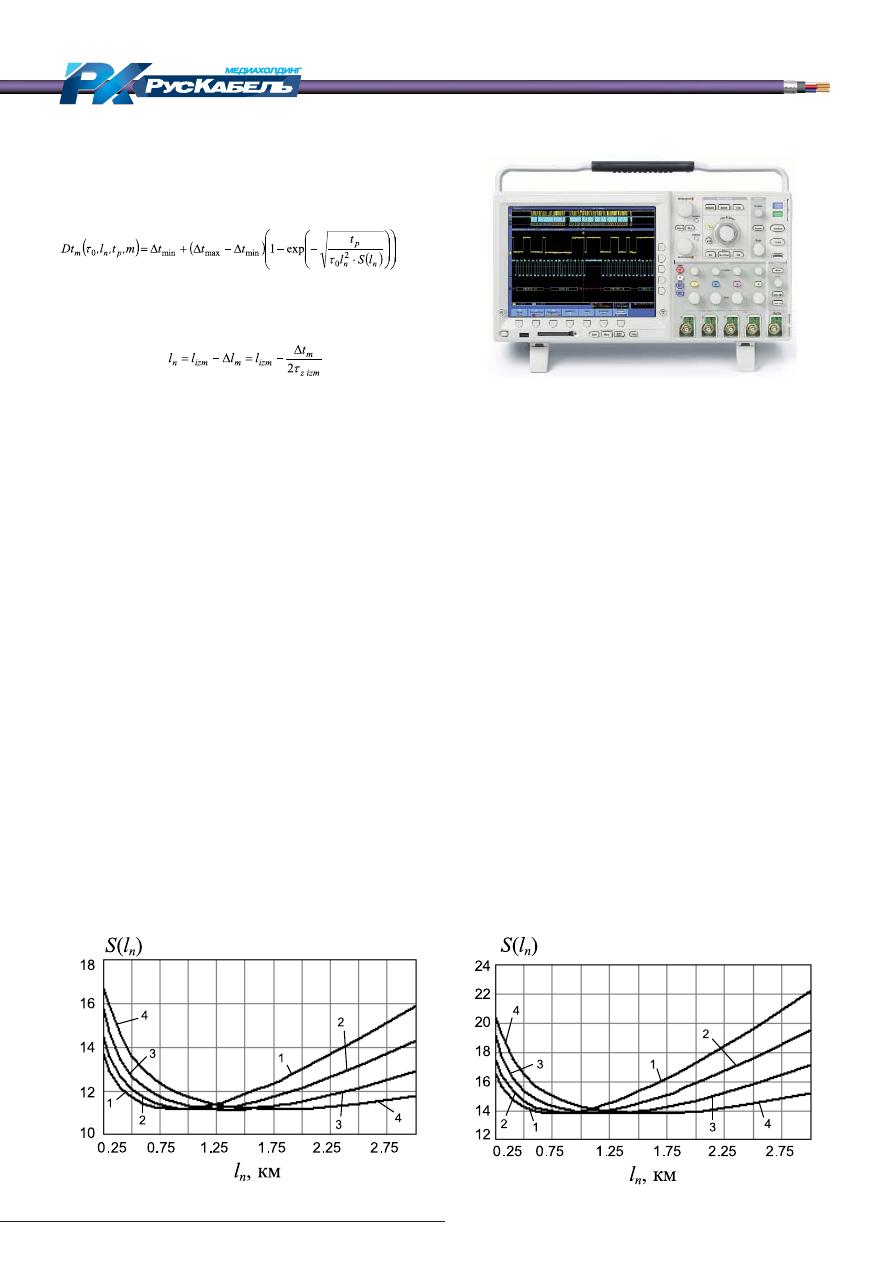
авторами предложена аппроксимирующая функция
вида:
. (20)
Графики функции
S(l
n
)
показаны на рис. 6.
Измеренное на уровне
m
расстояние
l
izm
можно
уточнить путём решения следующего уравнения:
,
(21)
где
l
n
— уточнённое расстояние до неоднородности.
Как уже отмечалось выше, величины
l
m
и
t
m
зави-
сят от
l
n
, то есть (21) необходимо решать численным
методом.
Была проведена экспериментальная проверка
эффективности предлагаемой методики обработки
результатов измерений, в ходе которой прибором
РЕЙС-205 регистрировались рефлектограммы обо-
рванных кабельных цепей ТПП-0,4 различной дли-
ны при различных длительностях зондирующих им-
пульсов. По рефлектограммам измерялись рассто-
яния до обрывов при различных значениях m и про-
водилось уточнение результатов измерений по вы-
ражениям (21) и (20). Результаты эксперименталь-
ного исследования представлены в табл. 2.
Представленные результаты обработки экспери-
ментальных данных доказывают, что погрешность
локализации резистивной неоднородности может
быть существенно уменьшена.
Предлагаемая методика реализуется с помощью
разработанного программного обеспечения. Для
распространения методики на любые кабельные
цепи необходимо проведение исследований этих це-
пей с целью определения зависимости
S
(
l
n
), входя-
щей в (20).
a
б
Рис. 6. Зависимости S(ln), полученные для m = 0,03 (а), m = 0,05 (б) и кабельных цепей:
1 — ТПП-0,32, 2 — ТПП-0,4, 3 — ТПП-0,5, 4 — ТПП-0,64
Авторы надеются заинтересовать измерителей
параметров кабельных цепей и установить с ними
полезные контакты. В настоящее время завершает-
ся работа по исследованию других методик повыше-
ния точности определения расстояний в кабельных
цепях.
ЛИТЕРАТУРА
1. Воронцов А.С., Фролов П.А. Импульсные измере-
ния коаксиальных кабелей связи. — М.: Радио и
связь, 1985.
2. Былина М.С., Глаголев С.Ф. Определение харак-
тера повреждения или неоднородности по реф-
лектограмме кабельной цепи. — Труды учебных
заведений связи № 168, СПб, 2002.
3. Андреев В.А. Временные характеристики кабель-
ных линий связи. — М.: Радио и связь, 1986.
4. Цифровой рефлектометр РЕЙС-205. Руковод-
ство по эксплуатации.
5. A. Clunie. Fault location for the cable manufacturer:
Technical Bulletin / Bicotest. — 1997.
6. Былина М.С., Глаголев С.Ф., Дюбов А.С. Оцен-
ка неоднородностей цепей кабелей для цифро-
вой передачи импульсным рефлектометром. —
КАБЕЛЬ-news, № 8, 2010.
Актуально
ÐÅÔËÅÊÒÎÌÅÒÐÈß
Оригинал статьи: Повышение точности определения расстояний по рефлектограммам кабельных цепей
Основной задачей импульсных измерений является определение расстояния до повреждения или неоднородности по зарегистрированной рефлектограмме. Однако на практике результаты измерений по рефлектограмме часто имеют большую погрешность. Данная работа посвящена повышению точности измерения расстояний рефлектометрическими цифровыми приборами.