78
Повышение точности алгоритмов
определения места повреждения
ЛЭП 6–35 кВ при двойных
замыканиях на землю с помощью
введения итерационных процедур
УДК 621.316.925.1
Куликов
А
.
Л
.,
д.т.н., профессор кафедры
«Электро энергетика,
электро
снабжение
и силовая электроника»
НГТУ им. Р.Е. Алексеева
Осокин
В
.
Ю
.,
аспирант кафедры
«Электроэнергетика,
электроснабжение
и силовая элек троника»
НГТУ им. Р.Е. Алексеева
Обалин
М
.
Д
.,
к.т.н.,
аспирант кафедры
«Электро энергетика,
электро снабжение
и силовая электроника»
НГТУ им. Р.Е. Алексеева
Ключевые
слова
:
двойное замыкание на
землю, определение места
повреждения, сеть с изоли-
рованной нейтралью, имита-
ционное моделирование
Keywords:
double earth fault, fault
location, network with isolated
neutral, simulation model
В
связи
с
высоким
износом
электрических
сетей
среднего
напряжения
задача
определения
места
повреждения
(
ОМП
)
является
приоритетной
.
В
статье
предложены
методы
повышения
точности
ОМП
при
двойных
замыканиях
на
землю
(
ДвЗЗ
)
в
сети
6–35
кВ
с
использованием
имитационного
моделирования
,
накопления
статистической
информации
и
компенсации
погрешностей
расчетов
по
результатам
моделирования
.
Разработан
способ
уточнения
расстояний
до
ДвЗЗ
на
разных
линиях
с
помощью
итерационного
пересчета
,
позволяющий
существенно
снизить
погрешность
расчета
и
сократить
необходимую
зону
обхода
поврежденной
линии
.
Работа
выполнена
при
финансовой
поддержке
Министерства
образования
и
науки
РФ
(
Соглашение
№
14.577.21.0244
о
предоставлении
субсидии
от
26.09.2017
г
.,
уникальный
идентификатор
проекта
RFMEFI57717X0244).
ВВЕДЕНИЕ
Задача определения места повреждения (ОМП) линии электропередачи
(ЛЭП) относится к сложным и наиболее длительным операциям по восста-
новлению поврежденных участков сети. В электрических сетях среднего
напряжения применяются, как правило, методы ОМП, основанные на од-
ностороннем замере параметров аварийного режима [1–3, 6–10], которые
позволяют рассчитать расстояние до междуфазных повреждений. Около
60–80% от общего числа повреждений в распределительных сетях 6–35 кВ
составляют однофазные замыкания на землю (ОЗЗ), определение которых
возможно с помощью дорогостоящих специализированных индикаторов
[4, 13]. Продолжительная работа сети при однофазном замыкании на землю
может привести к появлению повреждения на землю в другой точке сети (до
80% от числа устойчивых ОЗЗ). Второе замыкание на землю обычно возни-
кает на участке сети с наиболее ослабленной изоляцией и сопровождается
увеличением тока в поврежденных фазах, причем вторая точка замыкания
может располагаться как на линии, где уже произошло ОЗЗ, так и на дру-
гой линии, отходящей от шин распределительного устройства. Несмотря на
многообразие предлагаемых программно-аппаратных средств, проблема
ОМП при ДвЗЗ не имеет до настоящего времени общепризнанного реше-
ния [5–10], а современные методы, позволяющие рассчитать расстояние до
мест замыканий, обладают большой погрешностью.
АЛГОРИТМ
ОПРЕДЕЛЕНИЯ
МЕСТА
ПОВРЕЖДЕНИЯ
ПРИ
ДВОЙНЫХ
ЗАМЫКАНИЯХ
НА
ЗЕМЛЮ
НА
РАЗНЫХ
ЛИНИЯХ
В основе разработанного метода ОМП при ДвЗЗ на разных линиях лежит
имитационное моделирование и последующая статистическая обработ-
ка результатов [9–15]. Ниже приведены параметры имитационной моде-
ли для иллюстрации разработанного метода ОМП. Расчет расстояний до
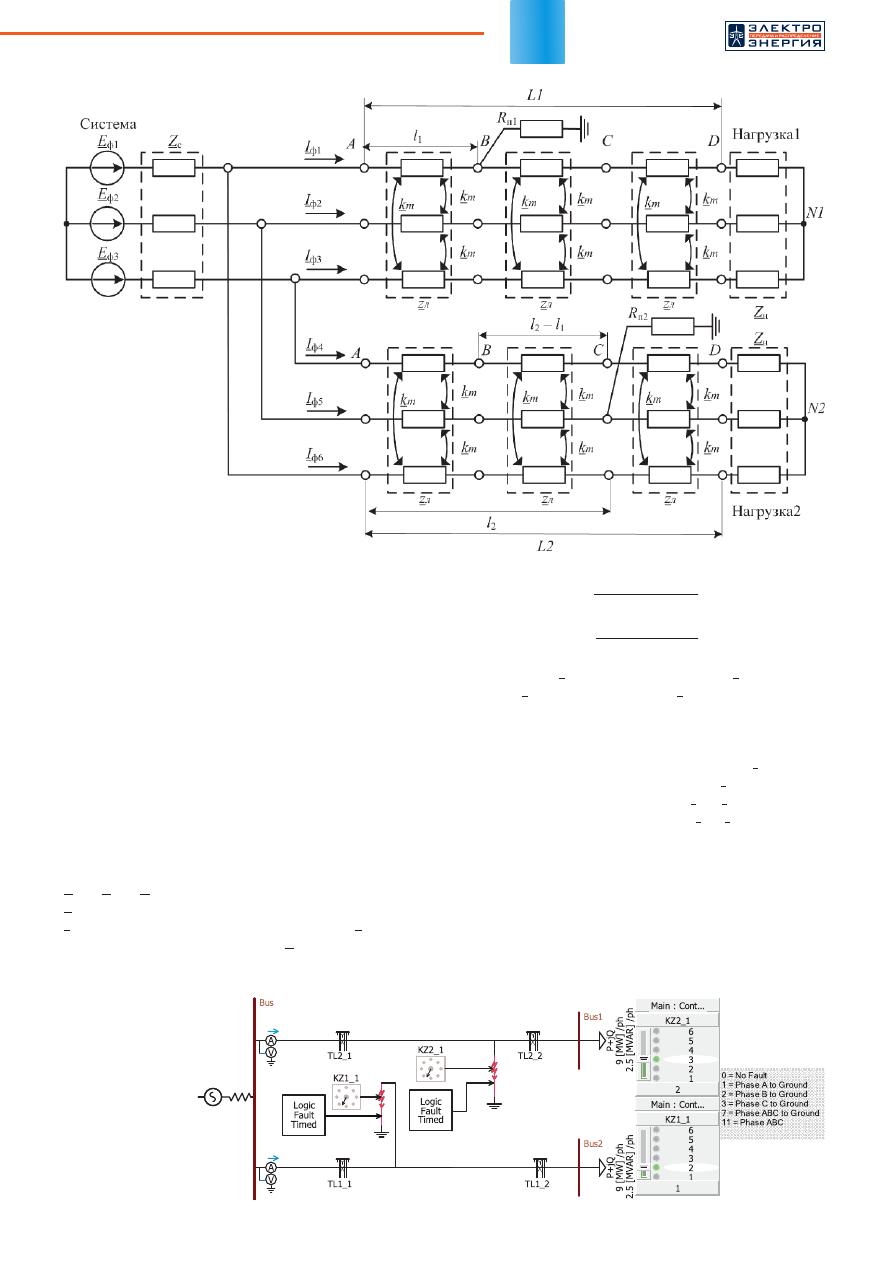
мест повреждений при ДвЗЗ на разных линиях выполняется по схеме, изо-
браженной на рисунке 1.
Составными частями переходного сопротивления
R
п
являются со-
противление дуги; сопротивление посторонних предметов между про-
ВОЗДУШНЫЕ
ЛИНИИ
79
водом и землей или опорой; сопротивление зазем-
ления опоры.
В процессе расчета и моделирования были при-
няты следующие допущения:
1) трехфазные элементы системы принимаются сим-
метричными;
2) не учитывается емкостная проводимость ЛЭП;
3) переходное сопротивление носит чисто активный
характер;
4) подпитка точки короткого замыкания током нагруз-
ки отсутствует.
Использование схемы, представленной на рисун-
ке 1, в фазных координатах [7] позволяет получить
выражения для определения расстояний до ближней
и дальней точек повреждения при ДвЗЗ на разных
линиях.
На рисунке 1 приняты следующие обозначения:
E
ф1
,
E
ф2
,
E
ф3
— эквивалентные ЭДС системы;
Z
c
— эквивалентное сопротивление сис темы;
z
л
— удельное сопротивление линии;
k
m
— коэф-
фициент взаимной индукции;
Z
н
— эквивалентное
сопротивление нагрузки;
R
п1
,
R
п2
— переходные
сопротивления
в мес тах замы-
каний;
l
1
,
l
2
—
ф а к т и ч е с к и е
расстояния до
мест ближне-
го и дальнего
замыканий на
землю.
В
общем
виде расчетные
выражения вы-
глядят следую-
щим образом:
Рис
. 1.
Схема
замещения
сети
в
режиме
двойного
замыкания
на
землю
на
разных
линиях
фазы
«
ф
1»
на
расстоянии
l
1
и
фазы
«
ф
2»
на
расстоянии
l
2
13
12
1
1
m
x
m
x
л
x
ф
X
l
,
(1)
23
21
2
2
m
x
m
x
л
x
ф
X
l
,
(2)
где
x
m
12
=
Im
(
z
m
·
I
ф11
/
I
ф21
),
x
m
13
=
Im
(
z
m
·
I
ф13
/
I
ф11
),
x
m
21
=
Im
(
z
m
·
I
ф21
/
I
ф22
),
x
m
23
=
Im
(
z
m
·
I
ф23
/
I
ф22
) — удель-
ные сопротивления взаимной индукций соседних
фаз относительно поврежденной;
X
ф1
,
X
ф2
— расчет-
ные индуктивные сопротивления, пропорциональ-
ные расстояниям до мест повреждений;
I
ф11
— ток
поврежденной фазы первой линии;
I
ф22
— ток по-
врежденной фазы второй линии;
I
ф12
,
I
ф13
— токи не-
поврежденных фаз первой линии;
I
ф21
,
I
ф23
— токи не-
поврежденных фаз второй линии.
Проверка предложенного способа ОМП проводи-
лась путем моделирования рассматриваемого ава-
рийного режима в программном комплексе PSCad
и Visual Basic по схеме, представленной на рисунке 2.
В рассматриваемой схеме приняты следующие пара-
метры:
– напряжение сети — 35 кВ;
Рис
. 2.
Модель
сети
напряжением
35
кВ
в
PSCad
при
двойном
замыкании
на
землю
на
разных
ЛЭП
№
1 (52) 2019
80
– длина линии:
L
1
= 10 км,
L
2
= 10 км;
– удельное сопротивление фазы:
z
л
= 0,079 +
j
0,697 Ом/км;
– удельное сопротивление взаимной индукции:
Z
m
= 0,0451 +
j
0,3536 Ом/км;
– переходные сопротивления в местах замыканий
определяются случайной величиной, распреде-
ленной по равномерному закону в диапазоне от
0 до 10 Ом;
– потребляемая мощность нагрузки:
S
н
= 9 +
j
2,5 МВА.
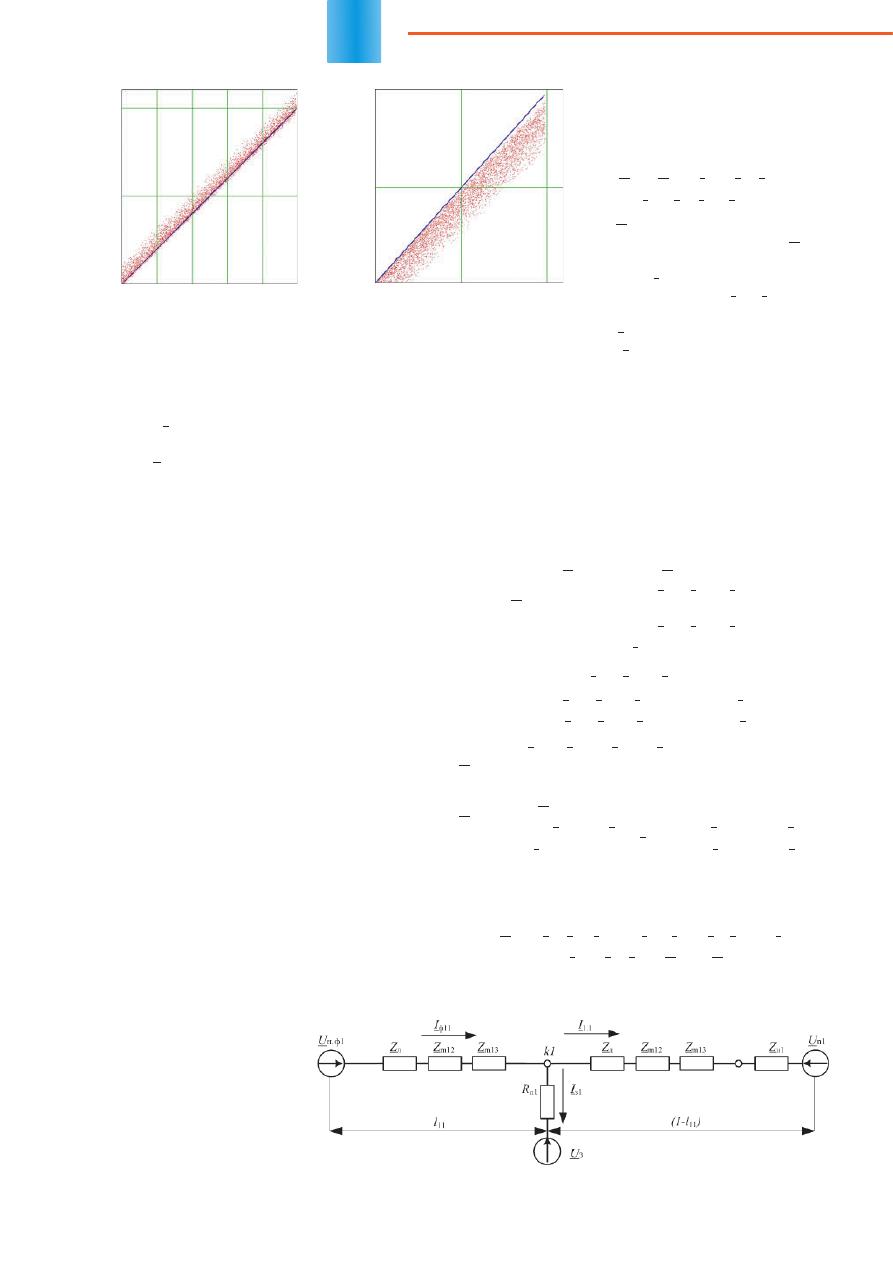
Обработка результатов моделирования позволя-
ет получить зависимости расчетных расстояний от
фактических значений (рисунок 3).
Анализ полученных результатов показывает, что
расстояние до первой точки повреждения (рису-
нок 3а) определяется с относительной погрешностью,
не превышающей 12%, а математическое ожидание
полученной погрешности составляет 3%. Расстояние
до второй точки повреждения (рисунок 3б) опреде-
ляется с относительной погрешностью, достигающей
26%, а математическое ожидание полученной по-
грешности составляет 7%.
Таким образом, представленный выше способ по-
зволяет определить область возникновения ДвЗЗ на
разных линиях электропередачи путем установки из-
мерительного органа сопротивления, включенного на
фазный ток и фазное напряжение отходящих линий.
УТОЧНЕНИЕ
РАССТОЯНИЙ
ДО
ПОВРЕЖДЕНИЙ
С
ПОМОЩЬЮ
ИТЕРАЦИОННОГО
ПЕРЕСЧЕТА
Для повышения точности алгоритма ОМП предлага-
ется использовать итерационное уточнение результа-
тов расчета расстояния до повреждения. В качестве
исходных данных используются
осциллограммы токов и напря-
жений, при установившемся ре-
жиме КЗ, а также значения рас-
стояний до мест повреждений,
полученные в первом приближе-
нии по формулам (1) и (2).
Далее представлен алгоритм
уточнения расстояния до точки
короткого замыкания, располо-
женной на первой линии.
Найдем значение напряжения
в нейтральной точке N1 (рису-
нок 1), по параметрам неповреж-
денной фазы:
U
n
1
=
(
U
н.ф1
–
I
ф12
∙
(
z
л
+
z
н1
))
–
(
I
ф13
∙
z
m
+
I
ф11
∙
z
m
∙
l
11
), (3)
где,
U
н.ф
— напряжение неповреж-
денной фазы первой линии;
U
n
1
—
напряжение в нейтральной точке
нагрузки;
I
ф11
— ток поврежденной
фазы первой линии;
I
ф12
,
I
ф13
— ток
неповрежденных фаз первой ли-
нии;
z
л
— удельное сопротивление
ЛЭП;
z
н1
— сопротивление нагрузки
на одну фазу;
l
11
— расстояние до
первой точки повреждения, полу-
ченное по формуле (1), относительно полной длины
линии.
Рассмотрим поврежденную фазу первой линии
(рисунок 1) с учетом взаимоиндукции соседних фаз
(рисунок 4).
Приняв во внимание тот факт, что сопротивление
эквивалентного участка, полученное по закону Ома,
равно сумме сопротивлений эквивалентной цепи, за-
пишем следующее выражение:
U
з
U
n
1
—
+
——
R
п1
(1
– l
11
) ∙ (
z
л1
+
z
m
12
+
z
m
13
)
U
н.ф1
–
——
1
1
—
+
——
R
п1
(1
– l
11
) ∙ (
z
л1
+
z
m
12
+
z
m
13
)
———
=
(4)
I
ф11
= (
z
л1
+
z
m
12
+
z
m
13
)
l
11
+
R
п1
((
z
л1
+
z
m
12
+
z
m
13
) ∙ (1
– l
11
) +
z
н1
)
+
——
R
п1
+ (
z
л1
+
z
m
12
+
z
m
13
) ∙ (1
– l
11
) +
z
н1
.
Пусть
z
л1
+
z
m
12
+
z
m
13
=
z
1
, а напряжение земли
U
з
= 0. Тогда с учетом преобразований полученное
выражение будет выглядеть следующим образом:
U
n
1
∙
R
п1
U
н.ф1
–
——
(1
–
l
11
)
∙
z
1
+
R
п1
+
z
н1
R
п1
∙
(
z
1
∙
(1
–
l
11
)
+
z
н1
———
=
z
1
l
11
+
———.
(5)
I
ф11
R
п1
+
z
1
∙
(1
–
l
11
)
+
z
н1
Выразив из данного выражения
R
п1
и взяв его аб-
солютное значение, получим формулу для опреде-
ления переходного сопротивления:
U
н.ф1
∙
(
z
1
+
z
н1
–
z
1
∙
l
11
)
–
I
ф11
∙
z
1
∙
l
11
(
z
1
–
z
1
∙
l
11
+
z
н1
)
R
п1
=
|
———
|
. (6)
I
ф11
∙
(
z
1
+
z
н1
)
– U
н.ф1
+
U
n
1
)
Зная значение переходного сопротивления в мес-
те возникновения дуги, можно получить величину
Рис
. 3.
Зависимость
расчетных
расстояний
до
точек
повреждения
ЛЭП
от
фактических
б)
а)
Фактические значения расстояния
до повреждения (м)
Рас
че
тные зна
чения расст
ояния
до повре
ждения (м)
1×10
4
1×10
4
5×10
3
5×10
3
0
Фактические значения расстояния
до повреждения (м)
Рас
че
тные зна
чения расст
ояния
до повре
ждения (м)
1×10
4
1×10
4
5×10
3
5×10
3
0
Рис
. 4.
Схема
замещения
поврежденной
фазы
первой
линии
при
двойном
за
-
мыкании
на
землю
ВОЗДУШНЫЕ
ЛИНИИ
81
тока, протекающего через переходное сопротивле-
ние:
U
н.ф1
– I
ф11
∙
l
11
(
z
1
+
z
m
12
+
z
m
13)
I
з1
=
——
,
(7)
R
п1
где
z
m
12
=
z
m
∙
I
ф12
/
I
ф11
и
z
m
13
=
z
m
∙
I
ф13
/
I
ф11
— сопротивле-
ния взаимной индукций первой линии относительно
поврежденной фазы;
I
ф11
— ток поврежденной фазы
первой линии;
R
п1
— переходное сопротивление в ме-
сте возникновения первого короткого замыкания.
Тогда по первому закону Кирхгофа можно опре-
делить ток подпитки точки короткого замыкания на-
грузкой:
I
1.1
=
I
ф11
– I
з1
.
(8)
Тогда с учетом изложенного выше пересчет напря-
жения в нейтральной точке N1 (рисунок 1) составит:
U
n
1
= (
U
н.ф1
– z
л1
I
ф12
– z
н1
I
ф12
)
– I
ф13
z
m
–
–
(
I
ф11
z
m
l
11
– I
1.1
z
m
(1
– l
11
)).
(9)
Решение выражения (4) относительно величины
l
11
сводится к получению квадратного уравнения, кор-
ни которого будут определять расстояние до точки
короткого замыкания. Получаем следующие выра-
жения для определения
l
11
:
______________
I
ф11
∙(
z
1
+
z
н
) + √
a
1
+
b
1
+
c
1
+
U
н.ф1
l
11
=
|
——
|
,
2 ∙
I
ф11
∙
z
1
______________
I
ф11
∙(
z
1
+
z
н
) – √
a
1
+
b
1
+
c
1
+
U
н.ф1
l
11
=
|
——
|
.
(10)
2 ∙
I
ф11
∙
z
1
Коэффициенты
a
,
b
,
c
составлены из следующих
выражений:
a
1
= (
I
ф11
∙
z
н
)
∙
(
I
ф11
∙
z
н
+ 2
I
ф11
∙
z
1
+ 4
R
п1
∙
I
ф11
–
2
U
н.ф1
);
b
1
= (
I
ф11
∙
z
1
)
∙
(
I
ф11
∙
z
1
+ 4
R
п1
∙
I
ф11
–
2
U
н.ф1
);
c
1
= 4
R
п1
∙
I
ф11
∙
(
U
n
1
– U
н.ф1
) +
U
2
н.ф1
.
Полученные зависимости (выражение 10) позво-
ляют уточнять расстояние до точки повреждения.
Для выбора единственного верного решения необхо-
димо сравнить полученные значения
l
11
с единицей
(величины получены в относительных единицах от
реальной длины линии).
На следующей итерации с учетом нового зна-
чения расстояния до повреждения по формуле (6)
производится уточнение значения переходного со-
противления. Далее по выражениям (8) и (9) опре-
деляются ток подпитки точки повреждения нагрузкой
и напряжение в точке N1. Далее с учетом уточненных
значений по выражению (10) определяется расстоя-
ние до точки повреждения. Итерационный процесс
продолжается, пока изменения значений, получен-
ные в двух последовательных итерациях, не станут
незначительными (не более требуемой ошибки рас-
чета расстояния до повреждения).
Аналогично определяется расстояние до точки
повреждения, расположенной на второй линии.
Проверка работоспособности предложенного ме-
тода ОМП проводилась с использованием схемы,
представленной на рисунке 2 с учетом результатов
моделирования в программном комплексе PSCad
и Visual Basic.
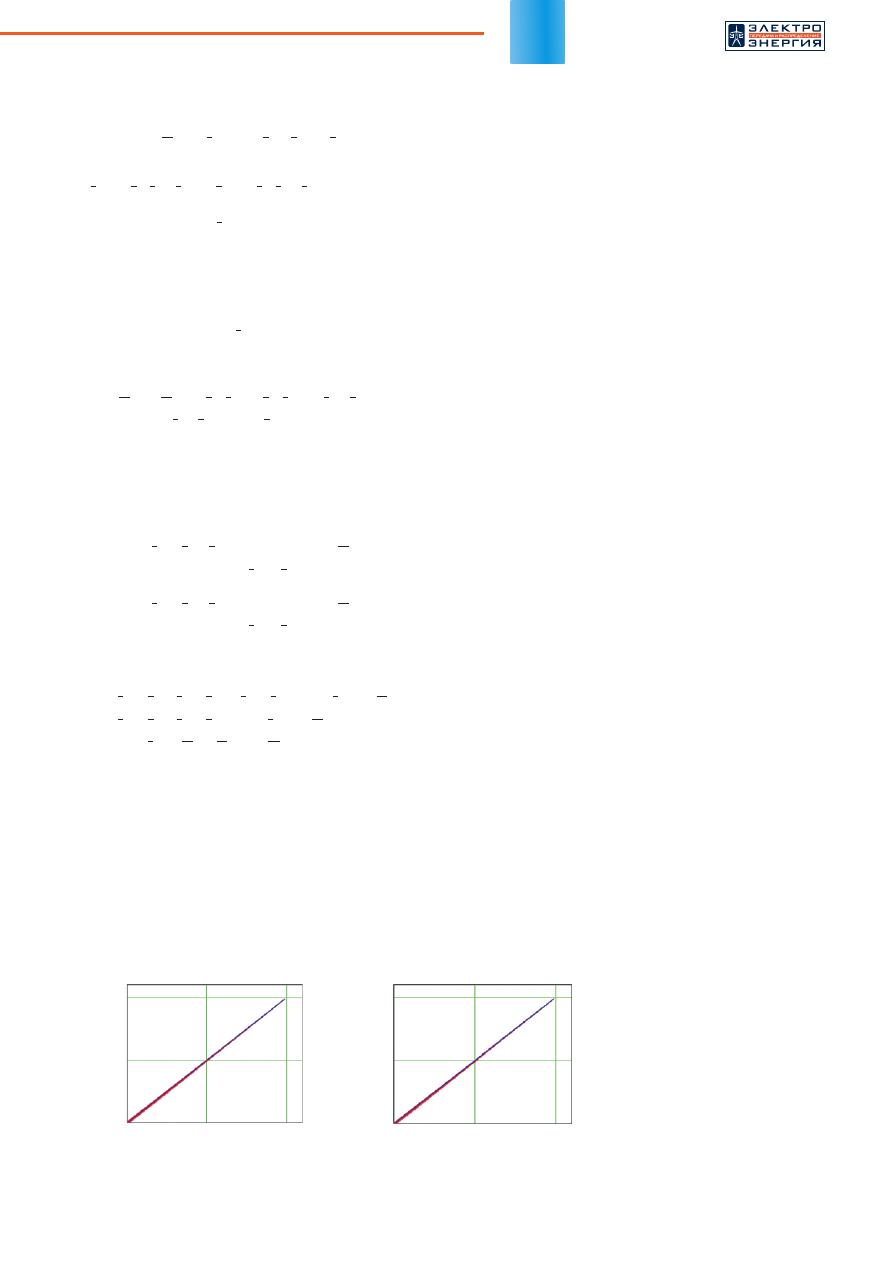
На рисунке 5 представлены зависимости расчет-
ных расстояний до ближней (а) и дальней (б) точек
повреждения ЛЭП от фактических. Анализ рисунка 5
подтверждает увеличение точности определения
расстояния и снижение ошибки расчета в сравнении
с первоначальными результатами. Максимальное
значение относительной погрешности расчета при
определении ближней точки замыкания составило
2,2%, а при определении дальней точки замыкания
составило 2,3%, что соответствует приблизительно
38 метрам.
ФОРМИРОВАНИЕ
ЗОНЫ
ОБХОДА
В
ПРЕДПОЛОЖЕНИИ
НОРМАЛЬНОГО
ЗАКОНА
РАСПРЕДЕЛЕНИЯ
ОШИБОК
ОМП
В основе организации поиска места повреждения
ЛЭП важным моментом является определение зоны
обхода поврежденной линии. Именно от размера
зоны обхода напрямую зависит время, необходимое
для проведения ремонтно-восстановительных работ
[8–10].
При наличии достаточно большого объема ста-
тистических данных о погрешностях ОМП можно
определить плотность вероятности распределения
ошибки относительно расчетного места поврежде-
ния. Целесообразно, задав доверительную вероят-
ность, получить доверительный интервал, который
будет задавать зону обхода ЛЭП.
Для формирования зоны обхода при ДвЗЗ на раз-
ных линиях, была определена плотность вероятно-
сти распределения абсолютных погрешностей рас-
чета относительно расчетного места повреждения
для каждого из возможных мест замыканий (рису-
нок 6).
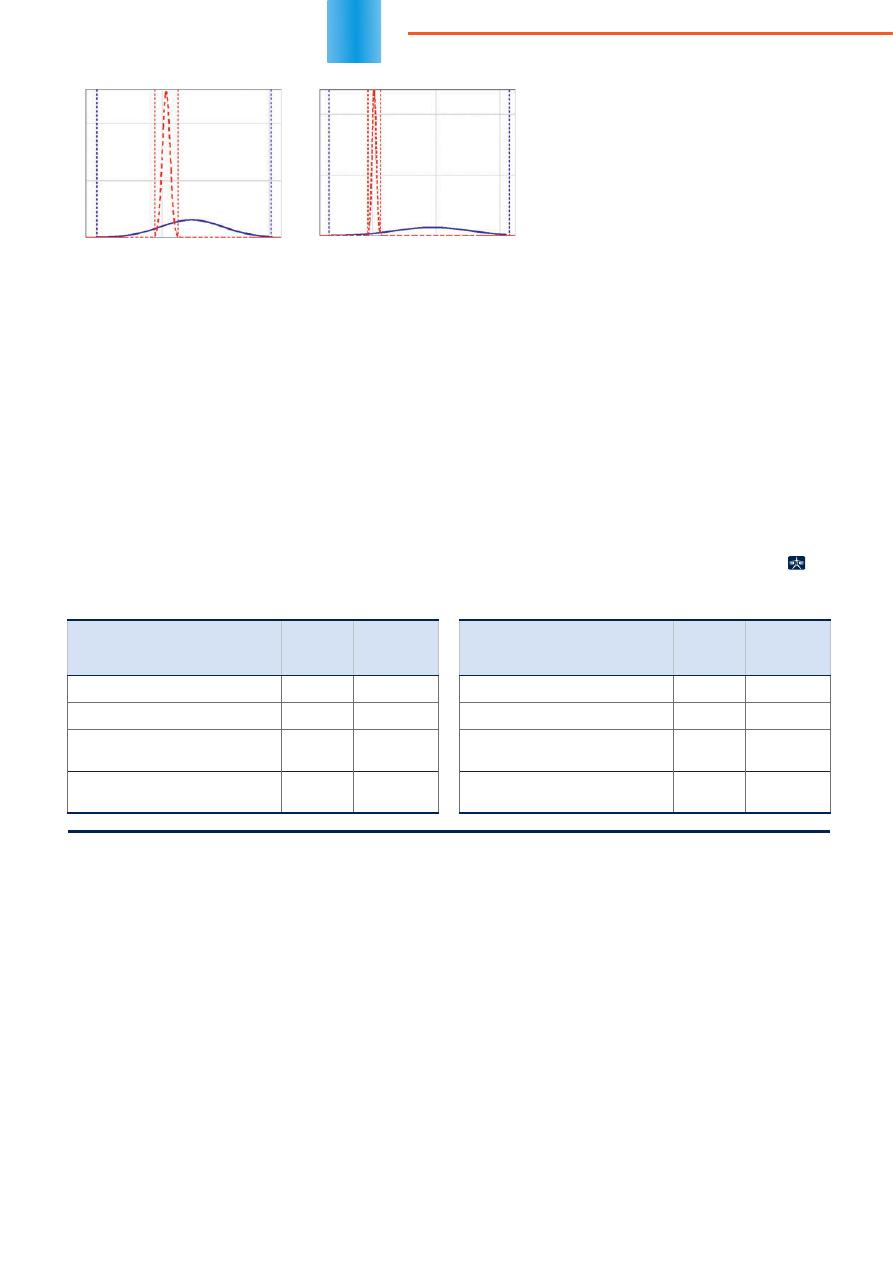
На рисунке 6а представлены плотности вероят-
ности абсолютной погрешности относительно рас-
четного значения расстояния
до ближней точки замыкания
(сплошная линия — до введе-
ния уточняющей итерационной
процедуры, штрихованная — по-
сле). По правилу трех сигм (3
)
был рассчитан доверительный
интервал, который соответствует
зоне обхода. Для точки замыка-
ния, полученной до итерацион-
ного расчета, зона обхода со-
ставляла 1,5 км (15% от общей
протяженности линии), а после
Рис
. 5.
Зависимость
расчетных
расстояний
до
ближней
(
а
)
и
дальней
(
б
)
точек
повреждения
ЛЭП
от
фактических
б)
а)
Фактические значения расстояния
до повреждения (м)
Рас
че
тные зна
чения
расст
ояния до повре
ж-
дения (м)
1×10
4
1×10
4
5×10
3
5×10
3
0
Фактические значения расстояния
до повреждения (м)
Рас
че
тные зна
чения
расст
ояния до повре
жде-
ния (м)
1×10
4
1×10
4
5×10
3
5×10
3
0
№
1 (52) 2019
82
итерационного пересчета зона обхода составила
0,2 км — 2%.
Результаты расчетов зоны обхода для примера
(рисунок 6а) приведены в таблице 1.
Использование итерационного расчета расстоя-
ния для уточнения ближней точки повреждения по-
зволило сократить зону обхода с 15% до 2% и тем
самым сократить время, необходимое для проведе-
ния аварийно-восстановительных работ.
На рисунке 6б представлены плотности веро-
ятности абсолютной погрешности относительно
расчетного значения расстояния до дальней точки
замыкания (сплошная линия — до введения уточ-
няющей итерационной процедуры, штриховая —
после).
Рис
. 6.
Примеры
графиков
плотности
вероятности
абсолютной
по
-
грешности
для
ближней
(
а
)
и
дальней
(
б
)
точек
повреждения
б)
а)
1
3
2
1
L1
L2
10
10
-1
-1
5
5
0
0
Для точки замыкания, полученной до
итерационного пересчета, зона обхода
составила 3,5 км — 35% от общей протя-
женности линии, а после итерационного
пересчета 1,3 км — 13%.
Результаты расчетов зоны обхода для
примера (рисунок 6б) приведены в таб-
лице 2.
Использование итерационного пере-
счета для уточнения дальней точки по-
вреждения позволило сократить зону
обхода с 35% до 2%, тем самым суще-
ственно сократить время, необходимое для ликвида-
ции повреждения.
ЗАКЛЮЧЕНИЕ
В статье предложены методы повышения точности
ОМП при ДвЗЗ в сети 6–35 кВ с использованием ими-
тационного моделирования, накопления статистиче-
ской информации и компенсации погрешностей ре-
альных расчетов по результатам моделирования.
Разработанный способ уточнения расстояний до
ДвЗЗ на разных линиях с помощью итерационного
расчета позволил существенно сократить зону обхода
поврежденной линии с 15% до 2% для ближней точки
повреждения и с 35% до 2% для дальней точки при
любых значениях переходного сопротивления.
Табл. 1. Результаты расчетов зоны обхода при ДвЗЗ
на разных линиях (ближняя точка повреждения)
До итера-
ционного
пересчета
После ите-
рационного
пересчета
Левая граница зоны обхода, км
–0,5
–0,06
Правая граница зоны обхода, км
1
0,13
Общая протяженность зоны
обхода, км
1,5
0,2
Общая протяженность зоны
обхода, %
15
2
Табл. 2. Результаты расчетов зоны обхода при ДвЗЗ
на разных линиях (дальняя точка повреждения)
До итера-
ционного
пересчета
После ите-
рационного
пересчета
Левая граница зоны обхода, км
–0,8
–0,07
Правая граница зоны обхода, км
2,7
0,13
Общая протяженность зоны
обхода, км
3,5
0,2
Общая протяженность зоны
обхода, %
35
2
ЛИТЕРАТУРА
1. Гловацкий В.Г., Халидов А.Г. Опре-
деление расстояния до мест двой-
ных замыканий на землю в элек-
трических сетях 35 кВ // Энергетик,
1985, № 9. С. 31.
2. Воробьева Е.А., Ганджаев Д.И.,
Филатова Г.А., Шуин В.А. Ин-
формационные параметры элек-
трических величин переходного
процесса для определения ме-
ста замыкания на землю в рас-
пределительных кабельных сетях
напряжением 6–10 кВ // Вестник
ИГЭУ, 2017, № 2. С. 34–42.
3. Хакимзянов Э.Ф., Мустафин Р.Г.,
Федотов А.И. Определение рас-
стояний до мест двойных замыка-
ний на землю на линии электро-
передачи распределительной сети
среднего напряжения // Известия
вузов. Проблемы энергетики,
2015, № 3–4. С.132–137.
4. Куликов А.Л., Мисриханов М.Ш.,
Петрухин А.А. Определение мест
повреждений ЛЭП 6–35 кВ мето-
дами активного зондирования.
Под ред. В.А. Шуина: М.: Энерго-
атомиздат, 2009. 162 с.
5. Висящев А.Н., Акишин Л.А. Тигун-
цев С.Г. Диагностика состояния
воздушных линий электропереда-
чи 10–110 кВ в нормальных и ава-
рийных режимах. Под ред. А.Н.
Висящева. Иркутск: Изд-во ИрГТУ,
2012. 270 с.
6. Геоинформационная система ОМП
6–35 кВ. URL: www.relematika.ru/pro-
dukty/6-35_kv/sistema_omp_6-35_kv.
7. Папков Б.В. Токи короткого за-
мыкания в электрических систе-
мах. Учеб. пособие. Новосибирск:
НГТУ, 2005. 275 с.
8. Беляков Ю.С. Актуальные вопросы
определения мест повреждения
воздушных линий электропереда-
чи // Библиотечка электротехника,
приложение к журналу «Энерге-
тик», 2010, № 11(43), 76 с.
9. Куликов А.Л., Обалин М.Д., Коло-
банов П.А. Комплексные алгорит-
мы ОМП ЛЭП на базе статистиче-
ских методов // Энергетик, 2012,
№ 1. С. 7–9.
10. Куликов А.Л., Обалин М.Д., Коло-
банов П.А. Анализ и повышение
точности при определении места
повреждения линий электропере-
дачи // Известия вузов. Электро-
механика, 2013, № 5. С. 57–62.
11. Diaz H., López M. Fault location
techniques for electrical distribution
networks / The Fifth IASTED Inter-
national Conference, 2005, pp. 311–
318.
12. Lehtonen M. Novel techniques for
fault location in distribution net-
ВОЗДУШНЫЕ
ЛИНИИ

83
works / Power Quality and Sup-
ply Reliability Conference, 2008,
pp. 1–6.
13. Куликов А.Л., Ананьев В.В. Адап-
тивное волновое определение ме-
ста повреждения линии электро-
передачи // Вестник ИГЭУ, 2014.
№ 4. С. 21–25.
14. Лачугин В.Ф., Панфилов Д.И.,
Смирнов А.Н. Реализация волно-
вого метода определения места
повреждения на линиях электро-
передачи с использованием ста-
тистических методов анализа дан-
ных // Известия РАН. Энергетика,
2013, № 6. С.137–146.
15. Куликов А.Л., Обалин М.Д., Осокин
В.Ю., Шарафеев Т.Р. Применение
имитационного моделирования
ЛЭП 6–35 кВ для повышения точ-
ности определения расстояния
до двойных замыканий на зем-
лю // Вестник ИГЭУ, 2018, № 1.
С. 40–49.
REFERENCES
1. Glovatskiy V.G., Khalidov A.G. Deter-
mining the distance to the places of
double earth faults in 35 kV electrical
networks.
Energetik
[Power engineer],
1985, no. 9, pp. 31. (in Russian)
2. Vorobyeva E.A., Gandzhayev D.I.,
Filatova G.A., Shuin V.A. Information
parameters of transient process elec-
trical quantities for determining earth
fault location in 6-10 kV distribution
cable networks.
Vestnik IGEU
[ISPU
Bulletin], 2017, no. 2, pp. 34-42. (in
Russian)
3. Khakimzyanov E.F., Mustafi n R.G.,
Fedotov A.I. Determining the distance
to the places of double earth faults on
the medium voltage power lines of
distribution network.
Izvestiya vuzov.
Problemy energetiki
[Proceedings of
the higher educational institutions.
ENERGY SECTOR PROBLEMS],
2015, no. 3¬–4. pp. 132–137. (in
Russian)
4. Kulikov A.L., Misrikhanov M.Sh.,
Petrukhin A.A.
Opredeleniye mest
povrezhdeniy LEP 6–35 kV meto-
dami aktivnogo zondirovaniya. Pod
red. V.A. Shuina
[6–35 kV power
lines damage location by active sens-
ing methods. Under the editorship of
Shuina V.A]. Moscow, Energoatomiz-
dat Publ., 2009. 162 p.
5. Visyashchev A.N., Akishin L.A.
Tiguntsev S.G.
Diagnostika sos-
toyaniya vozdushnykh liniy elektro-
peredachi 10–110 kV v normalnykh
i avariynykh rezhimakh.
Pod red.
A.N. Visyashcheva [Diagnostics of
10–110 kV overhead transmission
lines state in normal and emergen-
cy modes. Under the editorship of
Visyashchev A.N]. Irkutsk, INRTU
Publ., 2012. 270 p.
6.
Geoinformatsionnaya sistema OMP
6–35 kV
(Geoinformation system of
6–35 kV fault localization). Available
at: www.relematika.ru/produkty/6-35_
kv/sistema_omp_6-35_kV (accessed
July 17, 2017).
7. Papkov B.V.
Toki korotkogo za-
mykaniya v elektricheskikh siste-
makh
[Short-circuit currents in power
systems]. Novosibirsk, NSTU Publ.,
2005. 275 p.
8. Belyakov Yu.S. Topical issues of
determining overhead power lines
damage location.
Bibliotechka elek-
trotekhnika, prilozheniye k zhurnalu
"Energetik"
[Library for Electrical
Engineer — appendix to "Energetik"
journal], 2010, no. 11 (43), pp. 76. (in
Russian)
9. Kulikov A.L., Obalin M.D., Kolobanov
P.A. Complex algorithms for power
lines fault localization based on sta-
tistical methods.
Energetik
[Power
engineer], 2012, no. 1, pp. 7-9. (in
Russian)
10. Kulikov A.L., Obalin M.D., Kolo-
banov P.A. Analysis and accuracy
improvement when determining
power lines damage location. I
z-
vestiya vuzov. Elektromekhanika
[Russian Electromechanics], 2013,
no. 5. pp. 57–62. (in Russian)
11. Diaz H, López M, Fault location
techniques for electrical distribu-
tion networks // The Fifth IASTED
Inter national Conference, 2005,
pp. 311-318.
12. M. Lehtonen, Novel techniques for
fault location in distribution net-
works // Power Quality and Sup-
ply Reliability Conference, 2008,
pp. 1-6.
13. Kulikov A.L., Ananyev V.V. Adaptive
wave locating of power lines dam-
age.
Vestnik IGEU
[ISPU Bulletin],
2014, no. 4, pp. 21-25. (in Russian)
14. Lachugin V.F., Panfi lov D.I.,
Smirnov A.N. Implementation of
the wave method for determining
power lines damage location using
statistical methods of data analysis.
Izvestiya RAN. Energetika
[RAS
news. Power engineering], 2013,
no. 6. pp. 137–146. (in Russian)
15. Kulikov A.L., Obalin M.D., Osokin
V.Yu., Sharafeyev T.R. Application
of 6–35 kV transmission lines simu-
lation modeling for improving the
accuracy of double earth faults dis-
tance determination.
Vestnik IGEU
[ISPU Bulletin], 2018, no. 1, pp. 40-
49. (in Russian)
На правах рекламы
№
1 (52) 2019
Оригинал статьи: Повышение точности алгоритмов определения места повреждения ЛЭП 6–35 кВ при двойных замыканиях на землю с помощью введения итерационных процедур
В связи с высоким износом электрических сетей среднего напряжения, задача определения места повреждения (ОМП) является приоритетной. В статье предложены методы повышения точности ОМП при двойных замыканиях на землю (ДвЗЗ) в сети 6–35 кВ с использованием имитационного моделирования, накопления статистической информации и компенсации погрешностей расчетов по результатам моделирования. Разработан способ уточнения расстояний до ДвЗЗ на разных линиях с помощью итерационного пересчета, позволяющий существенно снизить погрешность расчета и сократить необходимую зону обхода поврежденной линии. Работа выполнена при финансовой поддержке Министерства образования и науки РФ (Соглашение № 14.577.21.0244 о предоставлении субсидии от 26.09.2017г., уникальный идентификатор проекта RFMEFI57717X0244).