100
диагностика и мониторинг
Особенности измерения
и балансов электроэнергии
при наличии гармоник
УДК 621.311.1
В
статье
приводится
анализ
методической
погрешности
,
воз
ни
кающей
при
определении
активных
мощностей
в
лини
ях
с
наличием
существенного
объема
гармони
чес
ких
составляющих
в
измеряемых
токах
и
напряжениях
.
Установлено
,
что
эта
погрешность
не
влияет
на
опреде
ления
баланса
активных
мощностей
в
узле
питания
,
но
может
давать
ошибки
в
измерении
активных
мощностей
линий
,
отходящих
от
этого
узла
.
Богдан
В
.
А
.,
к.т.н., начальник службы
электрических режимов
компании «Россети
Кубань»
Тропин
В
.
В
.,
д.т.н., профессор
Кубанского государ-
ственного аграрного
университета
им. И.Т. Трубилина
Богдан
А
.
В
.,
д.т.н., профессор
Кубанского государ-
ственного аграрного
университета
им. И.Т. Трубилина
Ключевые
слова
:
активная мощность,
измерение, несину со-
и дальный ток, напря-
жение, погрешность,
баланс, гармоники,
начальная фаза
А
ктуальность работы по точному составлению балансов мощно-
стей в узлах нагрузки определяется практической необходимо-
стью. Эта задача, согласно п. 6.2.8 ПТЭ, встречается в практике
работы энергетиков ежемесячно и в дни контрольных изме-
рений (режимные дни), когда необходимо каждый час в течение суток
(например, для ПС 110 кВ) при отсутствии телеизмерений отслеживать
показания соответствующих счетчиков электроэнергии. Причем, в полу-
чаемых данных может существовать несходимость балансов измере-
ний на отходящих линиях. В статье [1] это отмечается и указывается,
что при наличии в сети высших гармоник тока нагрузки у высокоточных
счетчиков электроэнергии класса 0,2S возникает значительная по ве-
личине дополнительная методическая погрешность измерения вплоть
до нескольких процентов, что и является основной причиной указанных
небалансов. Также в [1] говорится, что установка более точных средств
измерений поднимает планку ожидаемой точности и сходимости балан-
сов. Покажем, что в некоторых случаях небаланса точность счетчика не
является определяющей.
Счетчики высокой точности обычно включаются на подстанциях сетей
35, 110, 220 кВ, характеризующихся значительным индуктивным сопро-
тивлением объектов передачи, поэтому измеряемое напряжение
u
(
t
)
и
, по-
даваемое в соответствующем масштабе на счетчик, представим в виде:
u
(
t
)
и
=
E
(
t
) –
u
(
t
)
L
,
R
,
где
E
(
t
) =
E
m
sin
(
t
) — величина идеальной ЭДС эквивалентного генера-
тора сети;
u
(
t
)
L
,
R
— величина напряжения, падающего на эквивалентном
активно-индуктивном сопротивлении сети и созданного током нагрузки.
Ток нагрузки
i
(
t
), удовлетворяющий условиям Дирихле, представим
гармоническим рядом Фурье:
i
(
t
) =
A
1
sin
(
t
)
+ B
1
cos
(
t
)
+ A
2
sin
(2
t
)
+ B
2
cos
(2
t
)
+
+
A
3
sin
(3
t
)
+ B
3
cos
(3
t
)
+
...
где
A
i
, В
i
— величины амплитуд в масштабе соответственно синусных
и косинусных составляющих тока нагрузки.
Согласно основных принципов работы счетчика активной электро-
энергии нагрузки, в процессе измерения должны производиться после-
довательно три операции:
•
статическая
— мгновенное перемножение синфазных составляю-
щих (в данном случае синусных) сигналов тока
i
(
t
) и напряжения
u
(
t
)
и
и получения при этом сигнала мгновенной активной мощности
p
(
t
)
в виде соответствующего в масштабе мощности сигнала измери-
тельного напряжения, состоящего из полезного сигнала — посто-
янной составляющей
P
, равной по величине половине произведе-
ния амплитуд синусоидальных составляющих напряжения и тока
101
и тока, как составляющая полной мгновенной мощ-
ности
p
(
t
), даст множество постоянных составляю-
щих, но в результате их суммирования результирую-
щая постоянная составляющая будет отсутствовать.
Действительно, перемножая почленно ряды, полу-
чим пары слагаемых, которые содержат постоянные
составляющие:
p
(
t
)
2
= –
LA
1
B
1
cos
2
(
t
)
+
LB
1
A
1
sin
2
(
t
)
+
∞
+
p
1
(
sin
(
n
t
),
cos
(
n
t
)) – 2
LA
2
B
2
cos
2
(2
t
)
+
n
= 1
∞
+
2
LB
2
A
2
sin
2
(2
t
)
+
p
2
(
sin
(
n
t
),
cos
(
n
t
)) –
n
= 1
– 3
LA
3
B
3
cos
2
(3
t
)
+
3
LB
3
A
3
sin
2
(3
t
)
+
∞
+
p
3
(
sin
(
n
t
),
cos
(
n
t
)) – …
n
= 2
и так далее.
Нетрудно видеть, что квадраты синусов и косину-
сов, содержащие постоянные составляющие одного
знака в виде числа 0,5 при суммировании указанных
членов ряда дадут в результате нулевую постоянную
составляющую.
Таким образом, в первой динамической операции
должны быть подавлены составляющие, представля-
ющие сумму гармоник сигнала мгновенной мощности
всех частот от основной (50 Гц) до бесконечной.
В практических случаях расчета баланса интерес
представляет случай, когда определяется баланс по-
требления активной мощности при несинусоидаль-
ных токах. Рассмотрим схему, когда есть питающая
линия со счетчиком Wh и две отходящие линии со
своими счетчиками Wh1 и Wh2 (рисунок 2). Изме-
рительные преобразователи, трансформаторы тока
и напряжения считаем идеальными.
Покажем на конкретном примере влияние гармо-
ник тока на измерение активной мощности, постро-
енное по классическому методу электротехники [2]:
1
T
P
= –
∫
u
(
t
)
i
(
t
)
dt
,
T
0
где
u
(
t
) — напряжение в точке подключения счетчи-
ков и далее обозначенное как
u
(
t
)
и
.
ЭДС источника питания
E
(
t
) = 100
sin
(
t
) и значе-
ния токов:
i
1(
t
) = 4 {[
sin
(
t
)
cos
(
/4) –
cos
(
t
)
sin
(
/4)] –
– [
sin
(3
t
)
cos
(
/7) –
cos
(3
t
)
sin
(
/7)] / 10 –
– [
sin
(5
t
)
cos
(
/5)
+
cos
(5
t
)
sin
(
/5)] / 20},
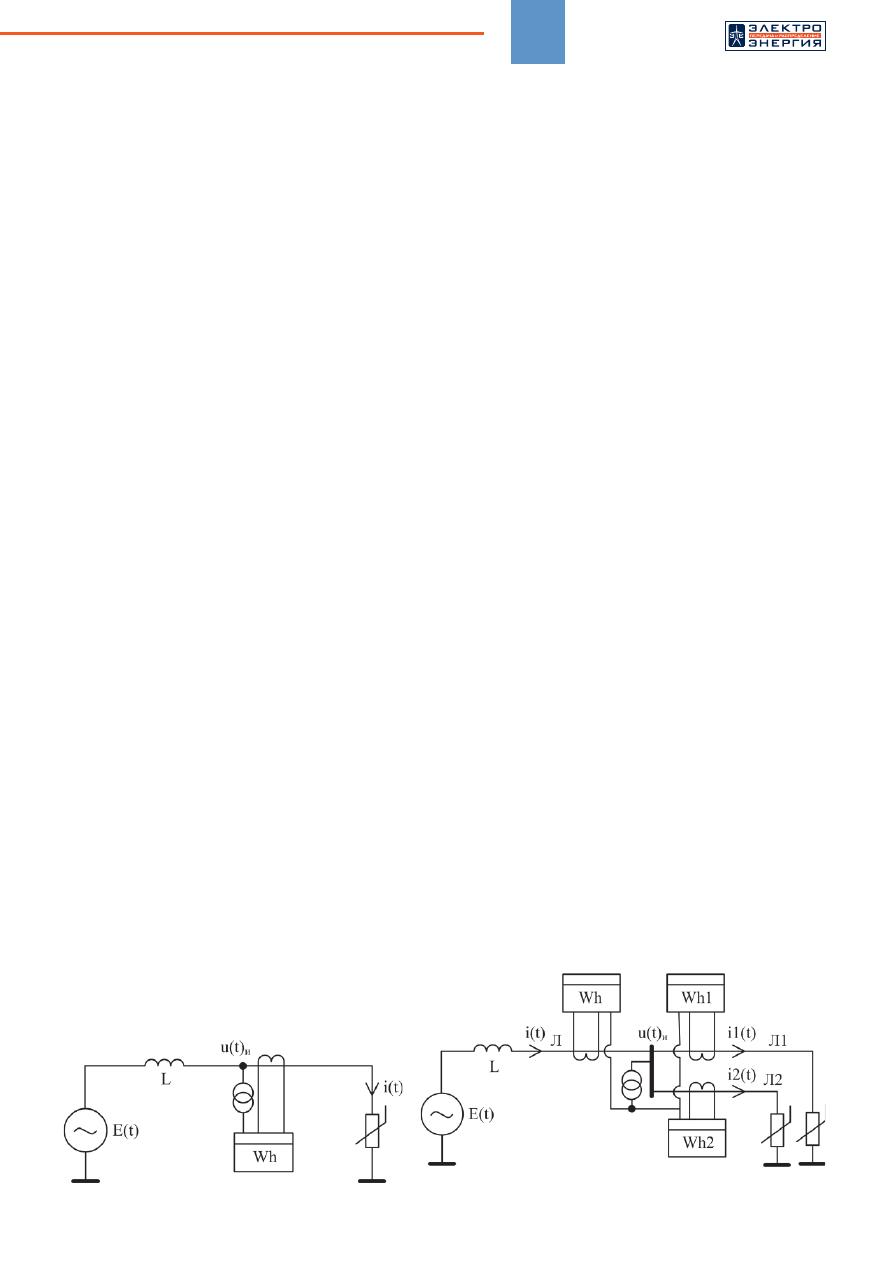
Рис
. 1.
Расчетная
схема
измерения
мощности
Рис
. 2.
Схема
соединения
счетчиков
для
определения
баланса
мощностей
линий
Л
,
Л
1
и
Л
2
основной (первой) гармоники (помехи, вызванной
действием перемножения двух синусоидальных
сигналов, имеющей частоту 100 Гц) и набора
гармонических помех с частотами 150 Гц и выше;
• две
динамические
: первая — выделение полез-
ного сигнала (постоянной составляющей сигнала
мгновенной мощности
P
) и вторая — текущее
интегрирование (постоянное накопление) полез-
ного сигнала на заданном интервале времени,
чтобы превратить полезный сигнал в искомый
сигнал
W
, пропорциональный величине количе-
ства потребленной нагрузкой электроэнергии
в соответствующем масштабе (в кВт·час).
Методическая погрешность в данном процессе
измерения возникает в том случае, если к полезному
сигналу
P
, определяемому измерительным напряже-
нием, по величине равным половине произведения
амплитуд синусоидальных составляющих напряже-
ния и тока основной (первой) гармоники, прибавля-
ются помехи в виде постоянных составляющих, воз-
никающие от действия перемноженных синфазных
составляющих сигналов гармонических помех.
Произведем аналитически указанные выше три
операции. Считаем, что активной составляющей
сопротивления в полном сопротивлении
Z
питаю-
щей сети (рисунок 1) можно пренебречь и учитывать
только индуктивную составляющую
L
. Тогда полу-
чим сигнал мгновенной мощности
p
(
t
):
p
(
i
) =
u
(
t
)
и
i
(
t
) =
E
(
t
)
i
(
t
) –
u
(
t
)
L
i
(
t
) =
=
E
m
sin
(
t
) · (
A
1
sin
(
t
) +
B
1
cos
(
t
)
+ A
2
sin
(2
t
)
+
+
B
2
cos
(2
t
)
+
...) –
L
di
/
dt
(
A
1
sin
(
t
)
+ B
1
cos
(
t
)
+
+
A
2
sin
(2
t
)
+ B
2
cos
(2
t
)
+
…),
где
L
di
/
dt
— величина напряжения, падающего на
индуктивном сопротивлении сети, которое равно:
u
L
=
L
· (
A
1
sin
(
t
) –
B
1
cos
(
t
)
+
2
A
2
sin
(2
t
) –
– 2
B
2
cos
(2
t
)
+
…).
Обращаем внимание на чередование знаков сла-
гаемых этого ряда.
Первое произведение
p
(
i
)
1
сигналов напряжения
сети и тока, как составляющая полной мгновенной
мощности
p
(
t
), даст только одну постоянную состав-
ляющую, которая и будет полезным искомым сигна-
лом
P
. Действительно:
1
∞
p
(
t
)
1
= —
E
m
A
1
+
p
0
(
sin
(
n
t
),
cos
(
n
t
)) =
2
n
= 2
∞
=
P +
p
0
(
sin
(
n
t
),
cos
(
n
t
)).
n
= 2
Второе произведение
p
(
t
)
2
сигналов напряжения,
падающего на индуктивном сопротивлении сети,
№
3 (54) 2019
102
i
2(
t
) = 4{[
sin
(
t
)
cos
(
/12)
+
cos
(
t
)
sin
(
/12)]
+
+
[
sin
(3
t
)
cos
(
/5)
+
cos
(3
t
)
sin
(
/5)] /10 –
+ [
sin
(5
t
)
cos
(
/7) –
cos
(5
t
)
sin
(
/7)]/20}.
В линии Л проходит суммарный ток
i
(
t
)=
i
1(
t
)
+ i
2(
t
).
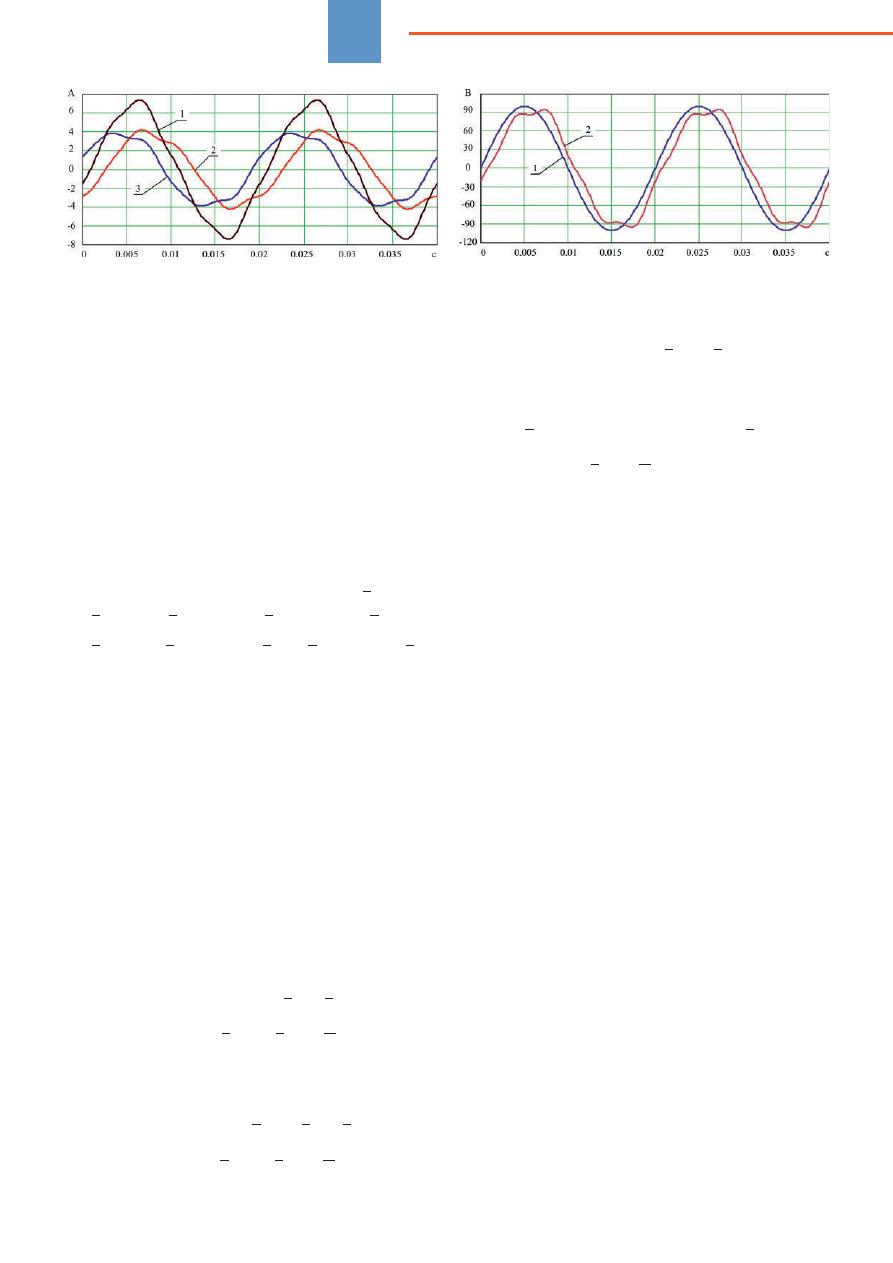
Форма токов при частоте
= 314 с
–1
показана на ри-
сунке 3. Относительное содержание гармоник в то-
ках
i
1(
t
) и
i
2(
t
) составляет 9,7%.
В точке измерения мощностей (рисунок 2) напря-
жение, подаваемое на трансформатор напряжения,
равно:
u
(
t
)
и
=
E
(
t
) –
u
(
t
)
L
,
для которого после дифференцирования получим:
u
(
t
)
и
= 100
sin
(
t
) –
L
·[
cos
(3
t
)/4 –
cos
(5
t
)/4 –
–
sin
(3
t
+
5
/14) –
sin
(5
t
+
5
/14)
+
3√2
cos
(
t
)
+
+
√6
cos
(
t
)
+
√5
cos
(3
t
)/4 – √5
cos
(5
t
)/4
+
3√2
sin
(
t
) –
_____________
_____________
– √6
sin
(
t
) – √2
sin
(3
t
)
√
5 – √5/4
+
√2
sin
(5
t
)
√
5 – √5/4].
Величина
L
выбрана таким образом, чтобы
падение напряжения на этом элементе было не-
большим. В рассматриваемом варианте расчета
действующее значение напряжения источника от-
личалось от измеряемого напряжения на 3%. Фор-
ма напряжения
u
(
t
)
и
в сравнении с неискаженным
напряжением источника питания показана на ри-
сунке 4.
Относительное содержание гармоник в напряже-
нии, подаваемом на счетчики, определяемое через
сумму квадратов амплитуд гармоник [3], равно вели-
чине 8,59%.
Расчет постоянных составляющих мгновенных
мощностей интегрированием произведения мгно-
венных значений токов и напряжений в узле измере-
ния дает следующие результаты:
• мощность для линии Л1:
1
0,02
P
1
= —
∫
i
1(
t
)
u
(
t
)
и
dt
= 100√2 – 5√5
sin
(
/7)/18 –
0,02
0
______________
– 5
sin
(
/7)/18
+
50√3/3 – 5√2
√
5 – √5
cos
(
/7)/18 =
= 169,31 Вт,
• мощность для линии Л2:
1
0,02
P
2
= —
∫
i
2(
t
)
u
(
t
)
и
dt
= 50√2 + 50√6 + 5√5
sin
(
/7)/18 +
0,02
0
______________
+ 5
sin
(
/7)/18
–
50√3/3 + 5√2
√
5 – √5
cos
(
/7)/18 =
=165,296 Вт,
• мощность для линии Л:
1
0,02
P
= —
∫
i
(
t
)
u
(
t
)
и
dt
= 150√2 + 50√6 = 334,6 Вт.
0,02
0
Видно, что мощность каждой из линий Л1 и Л2 со-
держит составляющие:
5√5
sin
(
/7)/18 – 5
sin
(
/7)/18
+
50√3/3 +
______________
+ 5√2
√
5 – √5
cos
(
/7)/18,
которые имеют разные знаки. Мощность питающей
линии Л равна сумме постоянных составляющих
линий Л1 и Л2, определенных по первым гармо-
никам, и, таким образом, баланс активных мощ-
ностей, приходящих в узел и уходящих из узла,
сходится абсолютно при наличии существенного
уровня гармоник тока и напряжения. В то же время
мощности линий Л1 и Л2 измеряются с ошибкой.
В [1] предлагается выделять сигнал основной ча-
стоты из полного сигнала и измерять его, после чего
вычислить углы сдвига и вычисления активной и ре-
активной мощностей. Разложим по Фурье величины
измеряемого напряжения и токов.
Первая гармоника измеряемого напряжения:
– синусная составляющая:
2
0,02
Us
(1)
= —
∫
u
(
t
)
и
sin
(
t
)
dt
= 92,5285 Вт.
0,02
0
– косинусная составляющая:
2
0,02
Uc
(1)
= —
∫
u
(
t
)
и
cos
(
t
)
dt
= –27,8839 Вт.
0,02
0
Первые гармоники токов
i
(
t
),
i
1(
t
) и
i
2(
t
):
– синусные составляющие:
2
0,02
Is
(1)
= —
∫
i
(
t
)
sin
(
t
)
dt
= 6,692 А;
0,02
0
2
0,02
I
1
s
(1)
= —
∫
i
1(
t
)
sin
(
t
)
dt
= 2,828 А.
0,02
0
2
0,02
I
2
s
(1)
= —
∫
i
2(
t
)
sin
(
t
)
dt
= 3,864 А.
0,02
0
– косинусные составляющие:
2
0,02
Ic
(1)
= —
∫
i
(
t
)
cos
(
t
)
dt
= –1,793 А;
0,02
0
2
0,02
I
1
c
(1)
= —
∫
i
1(
t
)
cos
(
t
)
dt
= –2,828 А.
0,02
0
2
0,02
I
2
c
(1)
= —
∫
i
2(
t
)
cos
(
t
)
dt
= 1,035 А.
0,02
0
Рис
. 3.
Расчетные
формы
токов
линий
: 1)
i
(
t
); 2)
i
1(
t
);
3)
i
2(
t
)
Рис
. 4.
Расчетные
формы
напряжений
: 1)
источника
питания
E
(
t
); 2)
точки
измерения
u
(
t
)
н
ДИАГНОСТИКА
И МОНИТОРИНГ

103
Получаем величины активных мощностей по ос-
новной гармонике с точностью определения состав-
ляющих ряда Фурье:
P
(1) = 0,5 · [
Us
(1) ·
Is
(1)
+
Uc
(1) ·
Ic
(1)] =
= 0,5 · [92,5285 · 6,692
+
27,8839 · 1,793] = 334,6 Вт,
P
1(1) = 0,5 · [
Us
(1) ·
I
1
s
(1)
+
Uc
(1) ·
I
1
c
(1)] =
= 0,5 · [92,5285 · 2,828
+
27,8839 · 2,828] = 170,29 Вт,
P
2(1) = 0,5 · [
Us
(1) ·
I
2
s
(1)
+
Uc
(1) ·
I
2
c
(1)] =
= 0,5 · [92,5285 · 3,864 - 27,8839 · 1,035] = 164,33 Вт.
Ошибка в определении активных мощностей по
линиям Л, Л1 и Л2 по классическому методу в срав-
нении с определением по первым гармоникам со-
ставляет:
P
–
P
(1)
334,6 – 334,6
P
Л
= — · 100 = — · 100 = 0%,
P
(1)
334,6
P
1
–
P
1(1)
169,31
–
170,29
P
Л1
= —
·100
= —
·
100
=
–0,575%,
P
1(1)
170,29
P
2
–
P
2(1)
165,296 – 164,33
P
Л2
= —
·100
= —
·100
=
0,595%.
P
2(1)
164,33
Отсюда следует вывод: методическая погреш-
ность определения значений активной мощно-
сти в условиях реальной сети с индуктивностями
в цепи тока может значительно влиять на измере-
ние токов индивидуальных линий, однако не влия-
ет на баланс мощностей в узле.
Методическая погрешность зависит от разности
начальных фаз гармоник измеряемых токов. Если
начальные фазы гармоник тока в расчете, прове-
денном выше, уменьшить в 3 раза, то получаем,
что погрешность измерения мощностей в Л1 и Л2
снижается до –0,229% и 0,238% соответственно.
Если разность начальных фаз токов гармоник бу-
дет одинакова для каждой гармоники, то методи-
ческая погрешность определения мощностей в Л1
и Л2 также становится равной нулю.
ВЫВОДЫ
1. Измерение активной мощности в линии, нахо-
дящейся за большим индуктивным сопротивле-
нием и питающей узел нагрузки, не зависит от
наличия высших гармоник токов нагрузки.
2. Наличие гармоник в токах отходящих линий
при индуктивном сопротивлении сети питания
создает методическую погрешность измерения
активных мощностей в линиях индивидуальных
потребителей.
3. Создаваемая методическая погрешность изме-
рения активных мощностей не влияет на ба-
ланс этих мощностей в узлах соединения линий
и уменьшается по мере уменьшения разности на-
чальных фаз гармоник токов в разных ли ниях.
ЛИТЕРАТУРА
1. Большаков О.В. Измерение электрических величин при
наличии гармоник // Спецвыпуск журнала «ЭЛЕКТРО-
ЭНЕРГИЯ. Передача и распределение», 2017, № 4(7).
С.14–16.
2. Демирчан К.С., Нейман Л.Р., Коровкин Н.В., Чечулин В.Л.
Теоретические основы электротехники: учебник для ву-
зов. В 3-х т. 4-е изд. Том 1. СПб.: Питер, 2003. С. 192–195.
3. Бессонов Л.А. Теоретические основы электротехники.
Электрические цепи: учебник для бакалавров. 11-е изд.,
перераб. и доп. М.: Юрайт, 2013. С. 218–220.
REFERENCES
1. Bolshakov O.V. Measurement of electrical quantities in the
presence of harmonics. ELECTRIC POWER. Transmission
and Distribution, 2017, no. 4(7), pp. 14-16. (in Russian)
2. Demirchan K.S., Neyman L.R., Korovkin N.V., Chechulin
V.L.
Teoreticheskiye osnovy elektrotekhniki
[Basic theory
of electrical engineering]. St. Petersburg, Piter Publ., 2003.
377 p.
3. Bessonov L.A.
Teoreticheskiye osnovy elektrotekhniki
[Ba-
sic theory of electrical engineering]. Moscow, Yurayt Publ.,
2013. 701 p.
Издательство журнала «ЭЛЕКТРОЭНЕРГИЯ. Передача и распределение»
выпустило книгу академика РАЕН, профессора В.А. НЕПОМНЯЩЕГО
Для приобретения издания звоните по
многоканальному телефону +7 (495) 645-12-41
или пишите по e-mail: info@eepir.ru
В монографии исследована надежность оборудова-
ния элек тро станций и электрических сетей напря-
жением 1150–10(6) кВ, разработана методика сбора
и статистичес кой обработки информации о надежности
оборудования. На основе статистических данных и рас-
четов определены основные параметры надежности
и динамика их изменения в процессе эксплуатации.
Выявлены статистические законы распределения отка-
зов и времени восстановления элементов энерго систем.
Проведено их сравнение с зарубежными данными.
№
3 (54) 2019
Оригинал статьи: Особенности измерения и балансов электроэнергии при наличии гармоник
В статье приводится анализ методической погрешности, возникающей при определении активных мощностей в линиях с наличием существенного объема гармонических составляющих в измеряемых токах и напряжениях. Установлено, что эта погрешность не влияет на определения баланса активных мощностей в узле питания, но может давать ошибки в измерении активных мощностей линий, отходящих от этого узла.