Оценка гибкости электроэнергетической системы с ветровыми станциями и накопителями энергии в режиме реального времени

Page 1

Page 2

возобновляемая энергетика

Оценка гибкости
электроэнергетической
системы с ветровыми
станциями и накопителями
энергии в режиме реального
времени

УДК 621.311.24:621.316

Глазунова

д.т.н., доцент,

старший научный

сотрудник отдела

электроэнергетических

систем Института систем

энергетики им. Л.А.

Мелентьева CО РАН

Аксаева

к.т.н., научный

сотрудник отдела

электроэнергетических

систем Института систем

энергетики им. Л.А.

Мелентьева CО РАН

Ключевые

слова

гибкость электро энер-

гетической системы,

детерминистические

методы, критерий

оптимальности

Внедрение

возобновляемых

источников

энергии

энергосистему

стало

причи

–

ной

появления

неопределенностей

параметров

режима

на

стороне

генерации

Необходимость

учета

этих

неопределенностей

при

управлении

электроэнер

–

гетической

системой

(

ЭЭС

)

превратила

задачу

оценки

гибкости

ЭЭС

одну

из

наиболее

важных

задач

оперативно

–

диспетчерского

управления

статье

пред

–

ставлен

детерминистический

метод

оценивания

гибкости

запланированного

(

нормального

)

режима

ЭЭС

ветровыми

станциями

накопителями

энергии

режиме

реального

времени

Метод

основан

на

утверждении

том

что

ЭЭС

обладает

гибкостью

если

имеется

возможность

компенсировать

небалансы

мощности

течение

рассматриваемого

времени

Сначала

вычисляется

сочета

–

ние

неопределенностей

(

отклонение

мощности

от

прогнозных

значений

)

на

–

грузочных

узлах

при

малом

превышении

которых

ЭЭС

становится

неспособной

поддерживать

баланс

мощности

(

теряет

гибкость

Данная

задача

решается

как

задача

линейной

оптимизации

качестве

критерия

оптимальности

использует

–

ся

максимальное

отклонение

значений

активных

нагрузок

от

запланированных

величин

учетом

заданных

ограничений

Затем

вычисляется

гибкость

ЭЭС

табильная и безопасная работа электроэнергетической сис-

темы (ЭЭС) возможна при наличии резервов для поддержа-

ния баланса мощности между генерацией и потреблением

в нормальных и послеаварийных режимах. В [1] нормальные

режимы характеризуются запланированными и незапланированными

изменениями параметров режима, которые определяются изменчиво-

стью и неопределенностью параметров режима энергосистемы соот-

ветственно. Неопределенности на стороне генерации мощности возни-

кают вследствие внедрения в ЭЭС зависимых от природных условий

возобновляемых источников энергии. Способность ЭЭС поддерживать

баланс мощности в условиях изменчивости и неопределенности в те-

чение заданного времени с учетом пропускных способностей связей

называется гибкостью ЭЭС [2]. В качестве резервов мощности или ис-

точников обеспечения гибкости [2] (далее источники гибкости от англ.

Sources of Flexibility) рассматриваются:

1. Резервная мощность генерации [3, 4]. Тепловые и гидроэлектро-

станции, обладающие свойством быстро увеличивать и сбрасы-

вать нагрузку, обеспечивают гибкость ЭЭС на стороне генерации.

Резервная мощность используется в случае незапланированного

увеличения или уменьшения нагрузки. В [2] рассматриваются проб-

лемы, связанные с резервами, представлена техническая класси-

фикация резервов и экономическая сторона вопроса. Отмечается,

что все имеющиеся резервы могут быть поделены на регулирующие

и аварийные. Регулирующие резервы предназначены для компен-

Page 3

сации неопределенностей на стороне спроса,

связанных с ошибкой прогноза потребления, и на

стороне генерации, возникающих из-за изменчи-

вости природных условий. В [3] дана информация

об оперативных резервах, используемых в США

и Европе. В [4] приведена методика определения

минимально необходимых объемов резервов ак-

тивной мощности ЭЭС России.

2. Механизмы управления активными потребителя-

ми [5, 6]. Разнообразные механизмы управления

нагрузкой, появившиеся в результате развития

новых технологий, решают проблему гибкости на

стороне потребителей. Механизмы управления

спросом применяются для корректировки мощ-

ности нагрузки: бытовой [7], сектора обслужива-

ния [8], промышленности [9].

3. Накопители энергии [10]. С внедрением ветровых

и солнечных электростанций важными средства-

ми обеспечения гибкости становятся накопители

энергии. Они используются для сохранения и вы-

дачи энергии в определенный отрезок времени.

Технологии сохранения энергии основываются на

разных физических принципах. На сайте [10] дана

следующая классификация накопителей: меха-

нические — это маховики, гидроаккумуляторы,

пневматические аккумуляторы; электрические —

конденсаторы и суперконденсаторы (ионисторы);

электрохимические — аккумуляторные батареи,

водородные топливные ячейки, нано-ионные

ячейки. В [11] описаны сверхпроводящие магнит-

ные накопители энергии, которые хранят энергию

в магнитном поле, созданном потоком постоянно-

го тока в катушке с нулевым электрическим со-

противлением, охлажденной ниже характерной

критической температуры.

4. Объединение ЭЭС [12]. При объединении ЭЭС

улучшается их гибкость, вследствие появления

возможности использовать имеющиеся в сосед-

ней ЭЭС резервы активной мощности. При нали-

чии ветровой электростанции в ЭЭС в случае из-

менения скорости ветра мощность, необходимая

для сохранения баланса, может быть получена по

межсистемным связям [12].

5. Создание мультиэнергетических систем [13]. При

создании мультиэнергетических систем (МЭС)

возникают дополнительные источники гибкости

ЭЭС. Мультиэнергетические системы, где элек-

тричество взаимодействует с другими секторами

энергии (охлаждение, отопление, транспорт, газ,

водород и т. д.), обладают большей гибкостью, чем

отдельно взятые электроэнергетические системы.

В [13] представлен подробный обзор работ, свя-

занных с оцениванием технической гибкости МЭС

и, в частности, распределенных МЭС, отмечается

высокий потенциал таких сис тем для поддержания

гибкости при внедрении возобновляемых источни-

ков энергии. Авторы статьи описывают ключевые

аспекты моделирования МЭС и вводят концепцию

«Мультиэнергетический узел».

Проблемы наличия, отсутствия и запаса гибкости

в энергосистеме решаются исследователями мно-

гих стран. В настоящее время разработаны вероят-

ностные, детерминистические методы определения

гибкости и методы, использующие искусственный

интеллект.

В [14] предлагается детерминистический метод

для определения диапазона максимальных неопре-

деленностей, при которых система остается гибкой

в течение указанного времени для заданной цены.

Метрика гибкости вычисляется в результате сравне-

ния полученного диапазона с целевым диапазоном.

Авторы [15] вычисляют гибкость термостатической

контролируемой нагрузки при подключении ее к сис-

теме. Множество допустимых графиков таких нагру-

зок представляется многогранником, агрегирован-

ная гибкость определяется как сумма Минковского.

В статье [15] описаны оптимизационные алгоритмы,

предложенные для аппроксимации многогранников

гомотетиями (преобразование подобиями) данного

выпуклого множества, представленного моделью

виртуальной батареи.

Авторы [16] разработали вероятностный метод

вычисления ожидания недостаточности ресурсов

для обеспечения гибкости (IRRE — the insuﬃ cient

ramping resource expectation). Для каждого на-

правления и временного горизонта формируется

распределение вероятности доступных ресурсов

гибкости. Авторы [17] рассчитывают остаток гибко-

сти, который является разницей между доступной

гибкостью и ожидаемым изменением нагрузки для

каждого наблюдения и временного горизонта. В ра-

боте определяется вероятность недостаточности

ресурсов в сис теме.

В [18] искусственная нейронная сеть (ИНС) ис-

пользуется для моделирования гибкости распреде-

ленных энергетических ресурсов. Обученная ИНС

оценивает, не нарушается ли гибкость конкретных

распределенных энергетических ресурсов при за-

данном (исследуемом) графике нагрузки. Преимуще-

ство этого подхода заключается в отсутствии необхо-

димости создавать точные модели распределенных

ресурсов.

В данной статье представлен детерминистиче-

ский метод оценивания гибкости запланированного

режима ЭЭС с накопителями энергии. Предложен

критерий для определения сочетания небалансов,

возникающих из-за ошибок прогноза (неопределен-

ностей) в нагрузочных узлах, при малом превыше-

нии которых ЭЭС становится неспособной поддер-

живать баланс мощности (теряет гибкость). Данная

задача решается как задача линейной оптимизации

с ограничениями в виде равенств и неравенств. Па-

раметром оптимизации является величина

, исполь-

зующаяся для моделирования разнообразных нагру-

зок. На основе предложенного критерия вычисляется

гибкость ЭЭС. Представление задачи определения

максимального отклонения от запланированного ре-

жима как задачи линейной оптимизации позволяет

уменьшить время вычисления гибкости ЭЭС. Струк-

тура статьи следующая: во втором разделе пред-

ставлена формулировка проблемы; в третьем раз-

деле описано моделирование источников гибкости

ЭЭС и моделирование различных нагрузок в нагру-

зочных узлах (в качестве источников гибкости рас-

№

3 (66) 2021

Page 4

сматриваются оперативные резервы и накопители

энергии); в четвертом разделе дана основная идея

метода, представлены критерий оптимальности и це-

левая функция вычисления максимальных нагрузок,

прописаны ограничения; в пятом разделе дано под-

робное описание метода вычисления гибкос ти; в ше-

стом разделе приведены результаты исследований;

в заключении представлены выводы, полученные

в результате анализа выполненной работы.

ФОРМУЛИРОВКА

ПРОБЛЕМЫ

Задача краткосрочного прогнозирования параметров

электроэнергетического режима является одной из

главных оперативно-диспетчерских задач, результа-

ты которой используются при управлении ЭЭС. Ре-

альный режим отличается от прогнозируемого из-за

наличия ошибок прогноза, которые складываются из

ошибок метода прогнозирования, непредвиденно-

го изменения мощности нагрузки, непредвиденного

изменения генерации на ветровой (солнечной) элек-

тростанции. Ошибки прогноза невозможно предска-

зать, поэтому они относятся к разряду неопределен-

ностей, которые в реальной ЭЭС представляются

в виде нерегулярного и кратковременного изменения

активной мощности. Компенсация небалансов мощ-

ности в таких случаях осуществляется за счет резер-

вов регулирования мощности (оперативный резерв).

Способность ЭЭС поддерживать баланс мощности

при нерегулярных и кратковременных изменениях

активной мощности в течение указанного време-

ни (в представленном исследовании) называется

гибкос тью ЭЭС. С целью оптимального управле-

ния режимами ЭЭС с ветровыми электростанциями

и с установленными нормативными объемами ре-

зервов предлагается оценивать гибкость ЭЭС в ре-

жиме онлайн. Полученная каждые несколько минут

информация о гибкости, включающая максималь-

ные значения и сочетания возможных небалансов

(неопределенностей), которые не приводят к дефи-

циту мощности, может быть использована в процес-

се оперативной коррекции режимов.

Данная работа посвящена проблеме определения

гибкости ЭЭС с ветровой электростанцией и аккуму-

ляторной батареей в режиме онлайн. Задача вычис-

ления гибкости нормального режима с упреждением

десять минут решается по следующему алгоритму:

– осуществляется сбор информации о параметрах

режима (поступает очередной срез измерений);

– выполняется прогнозирование режима с упреж-

дением 10 минут, прогнозный режим (далее —

запланированный) отличается от реального (неза-

планированного) из-за наличия ошибок прогноза;

– вычисляется гибкость прогнозного режима.

Для задач, выполняемых в режиме онлайн, од-

ним из главных требований является приемлемая

скорость получения решений. В предлагаемом авто-

рами алгоритме выполнение этого условия достига-

ется за счет введения ряда допущений и упрощений.

Допущения используются при выборе показателей

и средств гибкости. В качестве упрощений рассма-

триваются решение линейной оптимизационной

задачи и упрощенное вычисление перетоков мощ-

ности, которые требуются для записи ограничений.

С целью определения корректности полученных

с помощью линейной оптимизации результатов рас-

считывается установившийся режим методом Нью-

тона, где в качестве независимых переменных ис-

пользуются результаты оптимизации. Выявленная

разница между значениями мощности в балансиру-

ющем узле находится в заданных пределах.

МОДЕЛИРОВАНИЕ

ГИБКОСТИ

ЭЛЕМЕНТОВ

ЭЭС

МНОЖЕСТВА

НАГРУЗОК

В данной работе гибкость запланированного режима

ЭЭС характеризуется тремя показателями: скорость

изменения мощности (



), максимальная (мини-

мальная) генерации (

) и энергоемкость (

). Каждый

индекс является производной по времени от преды-

дущего индекса [2].

При вычислении гибкости ресурсов ЭЭС:

– допускается, что скорость включения гибкого

ресурса (



) равна времени упреждения, на кото-

рое вычисляется гибкость;

– учитывается показатель максимальной и мини-

мальной генерации (

);

– принимается во внимание, что конечная энер-

гоемкость батареи (

) ограничивает ее возмож-

ности.

Модель

гибкости

генераторов

на

традици

–

онной

станции

Гибкость генератора определяется

мощностью, которая может быть дополнительно сге-

нерирована на момент окончания рассматриваемого

горизонта и вычисляется по формуле:

(раб)

–

(тек)

(1)

где

(раб)

— рабочая мощность,

(тек)

— мощность

генератора в рассматриваемый момент времени.

Модель

гибкости

батареи

Гибкость батареи

определяется степенью заряженности батареи и те-

кущей мощностью. Если батарея заряжена в задан-

ных пределах,

SOC

min

SOC

(

) <

SOC

max

(2)

то отдаваемая мощность вычисляется по формуле:

(

max

)

–

(тек)

(3)

иначе

= 0,

(4)

где

SOC

— заряд батареи (state of charge),

SOC

min

—

минимальное значение заряда,

SOC

max

— макси-

мальное значение заряда,

(тек)

— мощность бата-

реи в рассматриваемый момент времени.

Модель

гибкости

системы

рассматривае

–

мый

момент

времени

Модель гибкости системы

записывается как сумма гибкостей, доступных на

всех объектах гибкости в рассматриваемый момент

времени. При наличии двух видов единиц гибкости

рассчитывается по формуле:



(5)

где

— количество генераторов на традиционных

станциях;

— количество батарей.

ВОЗОБНОВЛЯЕМАЯ

ЭНЕРГЕТИКА

Page 5

Моделирование

множества

разнообразных

нагрузок

Активная мощность нагрузки в каждом за-

данном узле

вычисляется по формуле [14]:

(

) =

min

+ (1 –

)

max

(6)

где 0 ≤

≤ 1,

max

— максимальная мощность нагруз-

ки в узле

min

— минимальная мощность нагрузки

в узле

Множество возможных нагрузок для

-го режи-

ма формируется по алгоритму, показанному на ри-

сунке 1.

ОСНОВНАЯ

ИДЕЯ

МЕТОДА

КРИТЕРИЙ

ОПТИМАЛЬНОСТИ

ЦЕЛЕВАЯ

ФУНКЦИЯ

ОГРАНИЧЕНИЯ

В основу разработанного метода положено утверж-

дение о том, что ЭЭС обладает гибкостью, если со-

блюдается баланс мощности в течение рассматрива-

емого времени при наличии неопределенностей со

стороны потребителей и производителей мощности.

При некотором сочетании нагрузок и значений ге-

нерации на ветровых (солнечных) электростанциях

для сохранения баланса в работу вводится весь ре-

зерв мощности, предназначенный для сглаживания

неопределенностей, который может быть передан

с учетом пропускных способностей связей. Такой

установившийся режим (УР) ЭЭС характеризуется

минимальной гибкостью (далее УР с минимальной

гибкостью), так как малое превышение нагрузки

в узле приведет к дефициту мощности в ЭЭС.

Задача вычисления УР с минимальной гибкос-

тью решается как задача линейной оптимизации.

Критерием оптимальности является максимальная

разность между значениями активных мощностей

в узлах с неопределенностью в запланированном

режиме и в режиме с минимальной гибкостью. Па-

раметрами оптимизации являются компоненты век-

тора

, отвечающие за моделирование величины

нагрузки в нагрузочных узлах от минимального до

максимального значений (рисунок 1).

Целевая функция — максимум суммы модулей

разностей между запланированными и смодели-

рованными мощностями в узлах с неопределенно-

стью — записывается следующим образом:

(

) =



= 1

–

(

)| =



= 1

|∆

(

)| →

max

, (7)

где

— номер узла с неопределенностью;

— про-

гноз активной мощности в узле

;

(

) — зависи-

мость активной мощности от величины

, отвечаю-

щей за изменение нагрузки в узле

i; r

— количество

узлов с неопределенностью. В данном случае это —

нагрузочные узлы, узлы, где выполняются управляю-

щие воздействия, и балансирующий узел.

Ограничения имеют следующий вид:





= 0,

(8)

–

(9)

min

УВ

max

(10)

min

max

(11)

0 ≤

≤1.

(12)

Ограничение (8) — это баланс мощности в узле

или

баланс мощности в ЭЭС, (9) — ограничение по про-

пускной способности линии, (10)–(11) ограничивает

диапазон управляющих воздействий (УВ) в управля-

емом и в балансирующем узлах, (12) — ограничение

на параметр оптимизации.

ОПРЕДЕЛЕНИЕ

ГИБКОСТИ

ЭЭС

Метрика

гибкости

Метрикой гибкости систе-

мы является величина, вычисленная в соответствии

с предложенным критерием оптимальности (7):



= 1

(

)



= 1

(

calc

(

) –

(13)

где

— активная нагрузка в узле

в запланирован-

ном режиме;

calc

(

) — величина нагрузки в узле

, вы-

численная по (6), где значения вектора

являются

результатом линейной оптимизации. Если

> 0, то

исследуемая ЭЭС является гибкой.

(

)

показывает

возможные отклонения мощностей в каждом нагру-

зочном узле от запланированного режима, с которы-

ми может справиться ЭЭС.

Задача

линейной

оптимизации

В процессе

оптимизации определяется вектор параметров

, ко-

торые используются для моделирования разнообраз-

ных нагрузок. Для решения поставленной задачи фор-

мируется целевая функция и ограничения (8)–(12).

ЦЕЛЕВАЯ

ФУНКЦИЯ

Каждый элемент (7) с учетом (6) может быть пред-

ставлен следующим образом:

(

) =



(

) = |

–

(

)|_ =

–

max

–

min

(14)

Начало (

= 1,

= 1)

Конец

Задаются векторы

min

= (

min

, …,

min

, …,

min

max

= (

max

, …,

max

, …,

max

)

(

— количество нагрузочных узлов)

Вычисляется значение нагрузки по (6)

Да

Нет

+ 1

step

Задается вектор

. Вычисляется шаг изменения мощ-

ности нагрузки:

step

= 1 /

= 1,

где

— число шагов,

— номер шага

Определение всех возможных значений нагрузок.

Результат: архив нагрузок

размерностью [

где

Рис

. 1.

Алгоритм

вычисления

множества

нагрузок

№

3 (66) 2021

Page 6

Величины, независящие от параметра оптимиза-

ции, обозначаются как

–

max

(15)

max

–

min

(16)

С учетом (14) целевая функция (7) записывается

как сумма слагаемых:

+ … +

→

max

(17)

и при исключении всех независимых от параметров

оптимизации величин имеет вид



= 1

| →

max

(18)

ОГРАНИЧЕНИЯ

Поиск оптимальных параметров выполняется с уче-

том ограничений в виде равенств и неравенств.

Ограничения в виде равенств — это балансы актив-

ной мощности в системе и в узлах с неопределенно-

стью. Ограничения в виде неравенств вводятся для

осуществления контроля за пропускной способно-

стью линий и за пределами мощностей в узлах с не-

определенностью. Параметры УР вычисляются при-

ближенно методом PTDF (power transfer distribution

factor — коэффициент распределения потоков мощ-

ности) [19]. С помощью коэффициентов, полученных

этим методом, учитываются изменения перетоков

активной мощности в линиях электропередачи при

изменении мощности в узле. Коэффициенты распре-

деления перетоков мощности в линии, ограниченной

узлами

, вычисляются заранее по формуле:

–



–



(

(19)





(

) =



= 1



(

(20)

где



— изменение мощности в узле, в котором вы-

полняются управляющие воздействия (размер УВ);



–

— изменение перетока мощности в линии

–

;



— изменение мощности в нагрузочном узле с не-

определенностью.

При решении задачи линейной оптимизации ко-

эффициенты

–

являются исходной информацией.

Ограничения

виде

равенств

Баланс мощности

в системе:





–



= 1

(

) +



= 0

(21)

c учетом (6) и после некоторых преобразований за-

писывается следующим образом:





= 1

(

) =



= 1

max



–



(22)

где

— количество узлов в системе;



— потери ак-

тивной мощности в системе. В работе допускается,

что потери меняются незначительно, вычисляются

в запланированном режиме и остаются постоянными.

Баланс мощности в узлах с неопределенностью

составляется в виде баланса приращений мощности:







= 1



–

= 0,

(23)





–



(

)

–

(24)

где



— приращение мощности инъекции в узле

(



–

(

);



–

— приращение мощности в ли-

нии

–

;

— количество смежных узлов.

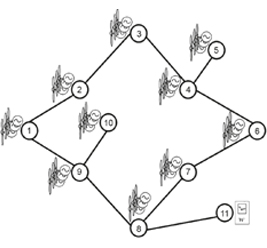
Рис

. 2.

Тестовая

схема

ВОЗОБНОВЛЯЕМАЯ

ЭНЕРГЕТИКА

С учетом (16), (24) ограничение в узле

записы-

вается:



= 1

–

= –

–

max



= 1

–

. (25)

Баланс мощности в балансирующем узле записы-

вается:



= 1

–

+ (

–



–

= (

max

–

)



= 1

–

max

–



= 1

max



= 1

(26)

где

≠

— номер балансирующего узла.

Ограничения в виде неравенств. Переток мощно-

сти в линиях контролируется по выражению (9):

–

∆

(

) <

–

max

(27)

или при переносе постоянных величин в правую

часть (с учетом (19) при

) ограничение имеет вид:

–

max

–

(

–

max

(28)

Ограничения по мощности в узлах с неопреде-

ленностью записываются следующим образом:

min

max

(29)

ПРАКТИЧЕСКИЕ

РЕЗУЛЬТАТЫ

Описание

тестовой

схемы

сценария

Разра-

ботанный метод применяется для вычисления гиб-

кос ти ЭЭС (рисунок 2), состоящей из 6 узлов и 6 ли-

ний. Узлами 1 и 5 обозначаются ветровая станция

и батарея. Узлы 2 и 6 представляют собой тради-

ционные станции. Узлы 3, 4 — это нагрузки. Узлами

с неопределенностью являются узлы 2, 3, 4, 6 (ба-

лансирующий). В узле 2 выполняются УВ.

Расчеты выполняются по сценарию: необходимо

вычислить гибкость ЭЭС для двух режимов на 10 ми-

нут вперед. Режимы отличаются друг от друга мощ-

ностью батареи.

Допускается, что за 10 минут включается весь

оперативный резерв, имеющийся на традиционной

станции, и батарея выдает максимальную мощность.

Максимальные и минимальные значения активных

мощностей в узлах с неопределенностью и активные

мощности двух УР в запланированных на 10 минут

вперед режимах показаны в таблице 1.

Вычисление

гибкости

узловой

схемы

Ре-

шение данной задачи может быть представлено не-

сколькими шагами.

Первый

шаг

Определение параметров режима

на 10 минут вперед (таблица 1).

Page 7

Второй

шаг

Вычисление коэффициентов

–

по

(19).

Третий

шаг

Описание целевой функции и огра-

ничений в соответствии с требованиями к входным

данным используемых программ.

Целевая функция

(

–

(

)) + (

–

(

)) +

+ (

–

(

)) + (

–

(

)) →

max

(30)

записывается следующим образом:



= 1

( –|

|) →

max

(31)

Аналогичные преобразования выполняются для

ограничений.

Баланс мощности в системе:

(

) –

(

) –

(

) +

(

) +



= 0 (32)

имеет вид:



= 1

(

) =

max

–

max

–

max

–



; (33)

балансы мощности в узлах 3 и 4:





3–1



3–4

= 0,

(34)





4–2



4–3

= 0

(35)

перерабатываются в уравнения:

(

3–1

3–4

) +

= (

–

max

) + (

–

max

)(

3–1

3–4

(36)

(

4–2

3–4

) +

= (

–

max

) + (

–

max

)(

4–2

3–4

(37)

Баланс мощности в балансирующем узле номер 6

записывается:

6–4

+ (

–

)

= (

max

–

)

6–4

max

–

max

–

max

(38)

Ограничения на пропускную способность в линиях

–

∆

(

) <

–

max

(39)

преобразуются к следующему виду:

1–2

–2

–

1–2

–

1–2

(

–

max

(40)

1–3

–3

–

1–3

–

1–3

(

–

max

(41)

1–5

–5

–

1–5

–

1–5

(

–

max

(42)

2–4

–4

–

2–4

–

2–4

(

–

max

(43)

3–4

–4

–

3–4

–

3–4

(

–

max

(44)

6–4

–4

–

6–4

–

6–4

(

–

max

(45)

Ограничения на параметры оптимизации:

0 ≤

≤1,

(46)

где

— номер узла (2, 3, 4, 6).

Ограничения вида (29) составляются по данным

таблицы 1.

Четвертый

шаг

Решение оптимизационной за-

дачи с учетом заданных ограничений, результатом

чего является вектор параметров оптимизации. По-

ставленная задача решается в среде Матлаб с ис-

пользованием функции linprog.

Пятый

шаг

Вычисление максимальных значе-

ний нагрузок в узлах 3, 4 и генерации в узлах 2, 6 по

формуле (6).

Шестой

шаг

Расчет установившегося режима

с полученными инъекциями. Исходным приближени-

ем напряжения являются значения модуля и фазы

напряжения в запланированном режиме, вычислен-

ные с помощью оценивания состояния.

Седьмой

шаг

Анализ полученного режима на

предмет существования данного режима. При отри-

цательном результате возможно выполнение ввода

режима в допустимую область.

Восьмой

шаг

Вычисление гибкости.

Анализ

результатов

Полученные результаты

сведены в таблице 2. В колонках 2, 5 расположены

значения активных мощностей, определенные в со-

ответствии с (6), где

— результат оптимизации.

В колонках 3,6 показана гибкость

(

)

. В предпо-

следней строке записана суммарная гибкость ЭЭС,

вычисленная по (13). В последней строке записана

суммарная гибкость ЭЭС, вычисленная в %. Для

проверки существования режима с инъекциями из

колонок 2, 5 рассчитывается УР (колонки 4, 7).

Анализ колонок 4 и 7 показывает, что УР1 и УР2

существуют (мощность в балансирующем узле не

превышает максимальную величину).

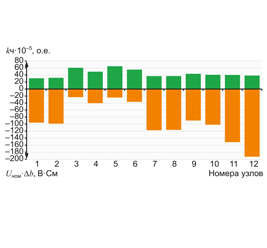
Значения максимальных мощностей (таблица 1,

колонка 2) и результаты оптимизации (таблица 2, ко-

лонки 2, 5) показаны на диаграмме рисунка 3.

Анализ результатов расчетов таблицы 2 и рисун-

ка 3 показывает, что:

Табл. 1. Исходная информация (МВт)

Номер

узла

max

min

УР1

УР2

14,6

–30

–26

–25

–16

0,0

6,7

–10

6,0

–0,4

Табл. 2. Результаты расчетов,

(МВт)

Номер

узла

УР1

УР2

calc

(

)

(

)

УР1

calc

(

)

(

)

УР2

14,6

29,5

–29,3

2,3

–29,3

–28,3

1,3

–28,3

–24,0

8,0

–24,0

–22,0

6,0

–22,0

0,3

9,8

7,5

6,5

9,9

10,3

7,3

(%)

26,1

18,5

№

3 (66) 2021

Page 8

• Сравнение заданных максималь-

ных нагрузок (таблица 1, курсив)

максимально

возможными

нагрузками, (таблица 2, жирный

шрифт), демонстрирует: первое,

вычисленные нагрузки не превы-

шают максимальные значения;

второе, если взять за 100% вели-

чину нагрузок в запланированном

режиме, то с учетом заданных

ограничений максимальные откло-

нения нагрузок составляют 13,5%

и 50% в УР1 (10% и 37,5% в УР2)

в узлах 3 и 4 соответственно.

• Гибкость рассматриваемой сис-

темы без учета аварийных ситу-

аций равна 10,3 МВт (26,1%)

и 7,3 МВт (18,5%) для УР1 и УР2

соответственно. Это означает, что при выдаче

максимальной мощности батареей наибольшее

отклонение нагрузок при условии возможности

восстановления баланса равно 10,3 МВт; при

выдаче минимальной мощности батареей наи-

большее отклонение нагрузок равно 7,3 МВт. Учет

аварийных ситуаций, вызванных нормативными

возмущениями, в упрощенном виде может быть

реализован путем вычитания величины норма-

тивного объема резерва из полученных значений

гибкости.

• При расчете УР, где в качестве исходных данных

используются значения мощностей, вычислен-

ные в результате оптимизации, выявлено, что

существование режима возможно при условии

корректировки активной мощности в балансиру-

ющем узле и мощность, полученная в результате

корректировки, находится в заданных пределах.

ВЫВОДЫ

В статье представлен критерий оптимальности, в со-

ответствии с которым вычисляется режим с макси-

мальными отклонениями нагрузок от запланиро-

ванных величин, в задаче определения гибкости

электроэнергетической системы. Для вычисления

сочетания максимальных отклонений используется

линейная целевая функция.

Выполнен расчет гибкости 6-узловой схемы, кото-

рая включает ветровую электростанцию, аккумули-

рующую батарею, две нагрузки и две генерирующие

станции. Сравнительный анализ значений гибкости,

вычисленных для разных режимов, показывает, что

величина гибкости ЭЭС зависит от режима в рас-

сматриваемый момент времени. Это подтверждает

необходимость определения гибкости в режиме ре-

ального времени на некоторое время вперед.

Выполнен анализ результатов линейной оптими-

зации на предмет существования режима. Выявле-

но, что для обеспечения балансов мощности в ЭЭС

при полученных в процессе оптимизации значениях

инъекций в узлах с неопределенностью мощности

в балансирующем узле должны быть скорректиро-

ваны.

-40

-30

-20

-10

МВт

Номер узла

Максимальные значения

Результат оптимизации УР1

Результат оптимизации УР2

Рис

. 3.

Диаграмма

активных

мощностей

ЛИТЕРАТУРА / REFERENCES
1. Ela E., Milligan M., Kirby B. Operating Reserves and Vari-

able Generation. Technical Report NREL/TP-5500-51978.

Contract no. DE-AC36-08GO28308, 2011.

2. Mohandes B., Shawky El Moursi M., Hatziargyriou N.,

El Khatib S. A Review of Power System Flexibility With

High Penetration of Renewables. EEE Transactions on

Power Systems, 2019, vol. 34, no. 4, pp. 3140-3155.

3. Rebours Y., D.s. Kirschen, Trotignon M., Sbastien Rossi-

gnol C. A survey of frequency and voltage control ancillary

services. Part I: technical features. IEEE Transactions on

Power Systems, 2007, vol. 22, no. 1, pp. 350-357.

4. Методика определения минимально необходимых объ-

емов резервов активной мощности ЕЭС России. URL:

https://so-ups.ru/fileadmin/files/company/markets/2014/

metodika_opredelenija_1114.pdf.

Procedure of determining the minimum required active

power reserves of UES of Russia. URL: https://so-ups.

ru/ﬁ leadmin/ﬁ les/company/markets/2014/metodika_opre-

delenija_1114.pdf.

5. Стенников В.А., Барахтенко Е.А., Соколов Д.В., Шеле-

хова В.Б. Активное участие потребителя в управлении

своим энергоснабжением // Известия высших учебных

заведений. Проблемы энергетики, 2017, т. 19, № 11–12.

С. 88–100.

Stennikov B.A., Barakhtenko E.A., Sokolov D.V., She-

lekhova V.B. Active role of consumers in their demand

management //

Izvestiya vysshykh uchebnikh zavedeniy.

Problemi energetiki

[News of higher educational establish-

ments. Power industry issues], 2017, vol. 19, no. 11–12,

pp. 88–100. (In Russian)

6. Сидорович В., Бокарев Б., Чаусов И., Кулешов М.,

Рычков С., Бурдин И. Управление спросом в электро-

энергетике России: открывающиеся возможности.

Экспертно-аналитический доклад. Инфраструктур-

ный центр EnergyNet, Москва, 2019. URL: https://www.

so-ups.ru/ﬁ leadmin/ﬁ les/company/markets/dr/publication/

EnergyNet_2019.pdf.

Sidorovich V., Bokarev B., Chausov I., Kuleshov M., Rych-

kov S., Burdin I. Demand management in the power in-

Исследование выполнено за счет средств гранта Россий-

ского научного фонда (проект № 19-49-04108).

ВОЗОБНОВЛЯЕМАЯ

ЭНЕРГЕТИКА

Page 9

dustry of Russia: opportunities. Expert-analytical report.

Infrastructural center EnergyNet, Moscow, 2019. URL:

https://www.so-ups.ru/ﬁ leadmin/ﬁ les/company/markets/dr/

publication/EnergyNet_2019.pdf.

7. Gottwalt S., Gärttner J., Schmeck H., Weinhardt C. Model-

ing and Valuation of Residential Demand Flexibility for Re-

newable Energy Integration. IEEE Transactions on Smart

Grid, 2016, vol. 8, no. 6, pp. 2565-2574.

8. Moradijoz M., Parsa Moghaddam M., Haghifam M.-R.

A Flexible Distribution System Expansion Planning mod-

el: dynamic bi level approach. IEEE Transactions on

Smart Grid, 2017. URL: https://www.researchgate.net/

publication/322205957_A_Flexible_Active_Distribution_

System_Expansion_Planning_Model_A_Risk-Based_Ap-

proach.

9. Gils H.Ch. Assessment of the theoretical demand response

potential in Europe. Energy, Elsevier, 2014, vol. 67, no. C,

pp. 1-18.

10. Накопители энергии. ИЦ «Автоматизация ресурсосбе-

регающих технологий». URL: http://www.ic-art.ru/kom –

pensatsiya-nagruzok-bespereboynoe-pitanie/setevie_

preobrazovateli/.

Energy storage units. Engineering Center ART. URL: http://

www.ic-art.ru/kompensatsiya-nagruzok-bespereboynoe-

pitanie/setevie_preobrazovateli/.

11. Суперпроводящий магнитный накопитель энергии. URL:

http://ru.knowledgr.com/00019040.

Superconductive magnetic energy storage. URL: http://ru.

knowledgr.com/00019040.

12. Bell K.R.W., Nedic D.P., Martin L.A.S.S. The need for in-

terconnection reserve in a system with wind generation.

IIEEE Transactions on Sustainable Energy, 2012, vol. 3,

no. 4, pp. 703-712.

13. Chicco G., Riaz Sh., Mazza A., Mancarella P. Flexibility

From Distributed Multienergy Systems. Proceedings of the

IEEE, 2020, vol. 108, no. 9, pp. 1496-1517.

14. Zhao J., Zheng, T., Litvinov E. A uniﬁ ed framework for deﬁ n-

ing and measuring ﬂ exibility in power system. IEEE Trans-

actions on power systems, 2016, vol. 31, no. 1, pp. 339-

347.

15. Zhao L., Zhang W., Hao H., Kalsi K. A Geometric Approach

to Aggregate FlexibilityModeling of Thermostatically Con-

trolled Loads. IEEE Transactions on power systems, 2017,

vol. 32, no. 6, pp. 4721-4731.

16. Lannoye E., Flynn D., O’Malley M. Evaluation of Power

System Flexibility. IEEE Transactions on Power Systems,

2012, vol. 27, no. 2, pp. 922-931.

17. Krommydas K.F., Stratigakos A.C., Dikaiakos C., Papaioan-

nou G.P., Zaﬁ ropoulos E.,. Ekonomou L. An Improved Flex-

ibility Metric Based on Kernel Density Estimators Applied

on the Greek Power System. International Symposium on

High Voltage Engineering, Budapest, Hungary, 2019. URL:

https://www.researchgate.net/publication/336921977.

18. Förderer K., Ahrens M., Bao K., Mauser I., Hartmut Sch-

meck H. Modeling ﬂ exibility using artiﬁ cial neural networks.

Proceedings of the 7th DACH+ Conference on Energy In-

formatics, 10 October 2018. URL: https://www.research-

gate.net/publication/328192598.

19. Ronellenﬁ tsch H., Timme M., Witthaut D. A Dual Method

for Computing Power transfer Distribution Factors. IEEE

Transactions on Power Systems, 2015, vol. 32, no. 2. URL:

https://www.researchgate.net/publication/282905950.

Ïðåîáðàçîâàòåëè
èçìåðèòåëüíûå
íàïðÿæåíèÿ ÏÈÍ
îò 50 Â äî 3000 Â

Âûñîêîâîëüòíûå

ýëåêòðîííûå

êëåùè ÊÒ-1000-Â

äëÿ èçìåðåíèÿ òîêà

äî 1000 À ïðè

íàïðÿæåíèè íà

òîêîâîé øèíå

äî 10 000 Â

Ïðåîáðàçîâàòåëè èçìåðèòåëüíûå

ìîùíîñòè ñåðèè ÏÈÌ

äëÿ êîíòðîëÿ àêòèâíîé ìîùíîñòè

â äèàïàçîíå îò 1 äî 4000 êÂò

Ïðåîáðàçîâàòåëè èçìåðèòåëüíûå

òîêà ñåðèè ÏÈÒ äëÿ èçìåðåíèÿ òîêà

îò 40 ìÀ äî 25 000 À

Преобразователи

(

датчики

)

для

энергетиков

от

ООО

НПО

Горизонт

Плюс

C=…,

nnn

&mon

&c%!,ƒ%…2

ãĊ

“[

(

h“2!=

l%“*%”“*%L

Ëąã

C!,K%!/

“%K“2″

……%L

!=ƒ!=K%2*,

ąã

,ƒ

äË

…,

2%*=

…=C! ›

…,

=*2,”…%L

%?…%“2,.

%K!=ƒ%”=2

Ëã

“

!2,-,

,!%”=…/

“…

“

…/

“

c%“!

ËË

“2!

Ëą

“2=”

%“2%L…3

ƒ=

äË

…3

C%!2…/

=…=

“%%2…%

ĈË

…,

ĆË

…=

ćË

“2″%.

C=…,

nnn

&mon

&c%!,ƒ%…2

ãĊ

“[

%“3?

“2″

“C

=2…3

%“2=”*3

%K!=ƒ%”=2

ËãË

“%

““

ËĄ

,%…/

“

“2!=…/

qmc.

www.g

riz

ont-pl

us.ru

%K!=ƒ%”=2

Ëã

(

,*,)

“C

Ëć

,”=

ãĉ

“=…,

ćË

“*3

,ƒ%

“

…/

“/

…/

ĆË

%K…/L

“/

…%L

,…2

L“

(4$

`).

www.g

riz

ont-pl

us.ru

На прав

ах рек

ламы

№

3 (66) 2021

Оригинал статьи: Оценка гибкости электроэнергетической системы с ветровыми станциями и накопителями энергии в режиме реального времени

Ключевые слова: управление спросом на электроэнергию, агрегатор спроса, киберфизическая структура

Читать онлайн

Традиционно основную роль в поддержании баланса мощности и энергии в ЭЭС выполняют электростанции. В современных условиях развития электроэнергетики появился новый востребованный инструмент регулирования баланса спроса и предложения на рынках электроэнергии — управление спросом на электроэнергию (от англ. Demand Response — DR). На основе материалов из доступных источников в статье анализируются критерии отбора участников в структуру агрегатора спроса в рамках пилотного проекта «Агрегатор спроса». Предлагается рассматривать процесс отбора как с учетом требований со стороны агрегатора к надежности функционирования участников, так и с учетом возможностей самих участников, рассматриваемых в статье с позиций киберфизической системы.