Проведен анализ теоретических и практических исследований пляски проводов воздушных линий электропередачи (далее — ВЛ) по материалам, опубликованным в мировой и отечественной периодической печати, а также по результатам опыта применения разработанных средств защиты проводов и грозозащитных тросов на действующих ВЛ. Рассмотрены физические и математические модели процесса и, учитывая низкую эффективность разработанных средств защиты от пляски проводов и грозозащитных тросов ВЛ, предлагаются новые подходы для исследования пляски проводов и колебания цепной линии как взаимосвязанных физических маятников с применением методов теории колебания механических систем.
Главная
Статьи
Статьи по категориям
О направлениях исследования пляски проводов на воздушных линиях электропередачи
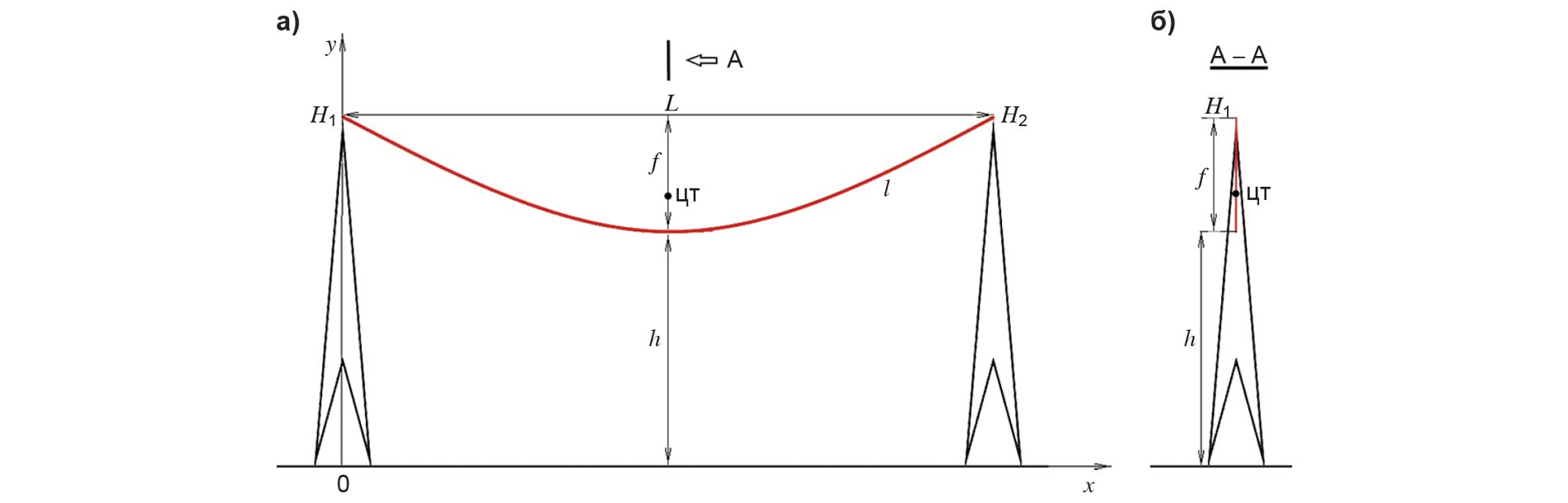
О направлениях исследования пляски проводов на воздушных линиях электропередачи
HTML-версия
УДК 621.3.051.2
Мирзаабдуллаев А.О.
«ЭЛЕКТРОЭНЕРГИЯ. Передача и распределение» № 3(78), май-июнь 2023