110
СЕТИ
РОССИИ
Модель
функционирования
релейной защиты
энергосистем
Приведена аналитическая модель функционирования релей-
ной защиты энергосистем, в которой учтены три вида отказов
и проверки работоспособности. Модель основана на описании
процесса функционирования полумарковским процессом. С по-
мощью этой модели получены такие показатели эксплуатации
и надежности, как коэффициент неготовности, средняя час тота
восстановлений, частоты неработоспособных состояний.
Андрей ТРОФИМОВ, к.т.н., доцент кафедры
Электрических станций НГТУ
Борис ЗЕЛЕНЦОВ, д.т.н., профессор кафедры
Высшей математики СибГУТИ
ВВЕДЕНИЕ
Обеспечение
структурной
(
аппа
-
ратной
)
надежности
и
эффективно
-
сти
функционирования
релейной
за
-
щиты
(
РЗ
)
требует
построения
таких
моделей
,
которые
пригодны
для
те
-
оретического
и
экспериментального
изуче
ния
их
свойств
.
Математическое
моделирование
является
наиболее
распространенным
и
перспективным
методом
изучения
этих
систем
,
кото
-
рое
позволяет
проводить
исследова
-
ние
на
этапе
проектирования
,
решать
задачи
анализа
и
синтеза
,
прогнози
-
ровать
качество
функционирования
и
эффективность
функционирования
релейной
защиты
,
обосновывать
их
необходимую
или
оптимальную
струк
-
туру
и
правильно
интерпретировать
статистические
данные
.
В
основе
ма
-
тематических
моделей
таких
сложных
систем
лежат
процессы
,
протекающие
при
их
функционировании
:
возникно
-
вение
и
устранение
отказов
,
проверки
состояния
оборудования
и
др
.
Целью
работы
является
разработ
-
ка
математической
модели
функци
-
онирования
РЗ
в
условиях
периоди
-
ческого
контроля
работоспособности
,
исследование
влияния
видов
отказов
РЗ
на
показатели
нажности
системы
РЗ
.
Результатом
такого
исследования
является
нахождение
зависимости
от
исходных
характеристик
таких
пока
-
зателей
,
как
коэффициент
неготовно
-
сти
,
среднее
время
наработки
на
от
-
каз
в
режиме
дежурства
,
вероятность
отказа
системы
РЗ
в
режимах
внеш
-
них
коротких
замыканий
(
КЗ
)
и
при
повреждении
защищаемого
объекта
,
влияние
периодичности
проверок
си
-
стемы
РЗ
на
показатели
надежности
и
эксплуатации
.
Построение
моделей
функциони
-
рования
системы
РЗ
неоднократно
обсуждалось
в
публикациях
[2, 10,
11].
Авторы
публикаций
[2, 11]
рассма
-
тривали
модель
надежности
системы
РЗ
с
одним
видом
отказа
,
а
именно
,
отказом
в
срабатывании
РЗ
.
Автор
работы
[10]
рассматривал
отказы
ви
-
дов
излишнего
срабатывания
и
отказ
в
срабатывании
.
Однако
в
системах
РЗ
имеют
место
другие
виды
отказов
;
при
этом
различают
три
вида
отказов
,
последствия
от
которых
для
энерго
-
р
е
л
е
й
н
а
я
з
а
щ
и
т
а
релейная защит
а

111
системы
будут
различны
.
Возникает
задача
оценки
влияния
отдельных
видов
отказов
РЗ
на
результирую
-
щие
показатели
надежности
.
Часть
отказов
РЗ
обна
-
руживается
функциональной
диагностикой
(
при
нали
-
чии
,
например
,
в
современных
устройствах
защиты
),
другая
часть
отказов
—
средствами
периодического
тестового
контроля
.
Показатели
надежности
играют
важную
роль
при
проектировании
систем
РЗ
,
а
также
при
обработке
статистических
данных
эксплуатируе
-
мых
систем
РЗ
.
С
учетом
этих
обстоятельств
предложена
модель
надежности
системы
РЗ
с
девятью
состояниями
,
ко
-
торая
является
достаточно
полной
для
расчета
ши
-
рокого
класса
показателей
надежности
,
отраженных
в
государственном
стандарте
[1].
ФУНКЦИОНИРОВАНИЕ
РЕЛЕЙНОЙ
ЗАЩИТЫ
ЭНЕРГОСИСТЕМ
Процесс
функционирования
РЗ
заключается
во
взаимодействии
различных
потоков
событий
(
возни
-
кающих
в
схеме
РЗ
дефектов
,
внутренних
и
внешних
коротких
замыканий
,
регулярного
потока
проверок
и
восстановлений
и
т
.
д
.)
с
устройством
РЗ
,
которое
может
находиться
в
различных
состояниях
[11].
Отказы
в
функционировании
релейной
защиты
подразделяются
на
три
основных
вида
:
–
ложные
срабатывания
(
срабатывания
защиты
в
режиме
дежурства
);
–
излишние
срабатывания
(
срабатывания
в
режимах
внешних
коротких
замыканий
);
–
отказы
в
срабатывании
(
отказы
в
срабатывании
защиты
при
повреждении
защищаемого
объекта
).
Обычно
существует
однозначная
связь
между
ви
-
дом
возникающих
в
схеме
дефектов
и
возможным
при
этом
видом
отказа
в
функционировании
.
Вслед
за
появлением
дефекта
,
опасного
с
точки
зрения
излиш
-
них
срабатываний
,
при
внешних
КЗ
может
произойти
излишнее
срабатывание
.
Если
в
схеме
присутствует
дефект
,
опасный
с
точки
зрения
отказов
защиты
при
повреждении
защищаемого
объекта
,
то
при
повреж
-
дении
этого
объекта
может
произойти
отказ
защиты
в
срабатывании
.
В
нерезервируемых
по
несрабатыва
-
нию
схемах
появление
дефекта
,
опасного
с
точки
зре
-
ния
ложных
срабатываний
,
может
сразу
же
привести
к
ложным
срабатываниям
защиты
.
Возможны
дефекты
,
опасные
с
точки
зрения
двух
и
более
видов
отказов
РЗ
в
функционирова
-
нии
,
например
,
дефекты
,
способные
при
опреде
-
ленных
условиях
привести
к
излишним
или
ложным
срабатываниям
.
В
некоторых
случаях
изменение
схемы
или
уста
-
вок
защиты
может
изменить
«
связь
»
дефекта
и
воз
-
можного
вида
отказа
защиты
.
Например
,
введение
пусковых
органов
,
препятствующих
срабатыванию
защиты
в
режиме
дежурства
,
может
«
перевести
»
дефекты
,
опасные
с
точки
зрения
ложных
срабаты
-
ваний
,
в
разряд
опасных
с
точки
зрения
излишних
срабатываний
и
т
.
д
.
Повышение
тока
срабатывания
продольной
дифференциальной
защиты
генератора
выше
номинального
приводит
к
переходу
обрыва
то
-
ковой
цепи
плеча
защиты
из
категории
неисправно
-
стей
,
опасных
с
точки
зрения
ложных
срабатываний
,
в
опасные
с
точки
зрения
излишних
срабатываний
.
ГРАФ
СОСТОЯНИЙ
Рассмотрим
вариант
модели
с
девятью
состояни
-
ями
системы
РЗ
,
которые
пронумерованы
от
1
до
9:
1)
Р
—
работоспособное
состояние
системы
РЗ
;
2)
Ф
И
—
функционирование
релейной
защиты
с
на
-
личием
дефекта
с
точки
зрения
излишнего
сраба
-
тывания
;
3)
Ф
О
—
функционирование
релейной
защиты
с
на
-
личием
дефекта
с
точки
зрения
отказа
в
срабаты
-
вании
;
4)
О
Л
—
отказ
релейной
защиты
вида
«
ложное
сраба
-
тывание
»;
5)
О
И
—
отказ
релейной
защиты
вида
«
излишнее
сра
-
батывание
»;
6)
О
О
—
отказ
релейной
защиты
вида
«
отказ
в
сраба
-
тывании
»;
7)
ПР
—
проверка
системы
РЗ
,
находящейся
в
рабо
-
тоспособном
состоянии
;
8)
ПН
—
проверка
системы
РЗ
,
находящейся
в
нера
-
ботоспособном
состоянии
;
9)
В
—
восстановление
работоспособности
.
Принято
,
что
события
,
приводящие
к
смене
со
-
стояний
,
являются
случайными
и
время
до
этих
со
-
бытий
распределено
по
экспоненциальному
закону
.
Тогда
переходы
между
состояниями
характеризуются
следующими
постоянными
интенсивностями
:
И
—
интенсивность
излишних
срабатываний
;
Л
—
ин
-
тенсивность
ложных
срабатываний
;
О
—
интенсив
-
ность
отказов
в
срабатывании
;
П
—
интенсивность
проверки
;
П
—
интенсивность
завершения
провер
-
ки
;
В
—
интенсивность
завершения
восстановления
(
интенсивность
восстановления
),
И
—
интенсивность
внешних
КЗ
(
вне
защищаемого
объекта
),
О
—
интен
-
сивность
внутренних
КЗ
(
на
защищаемом
объекте
).
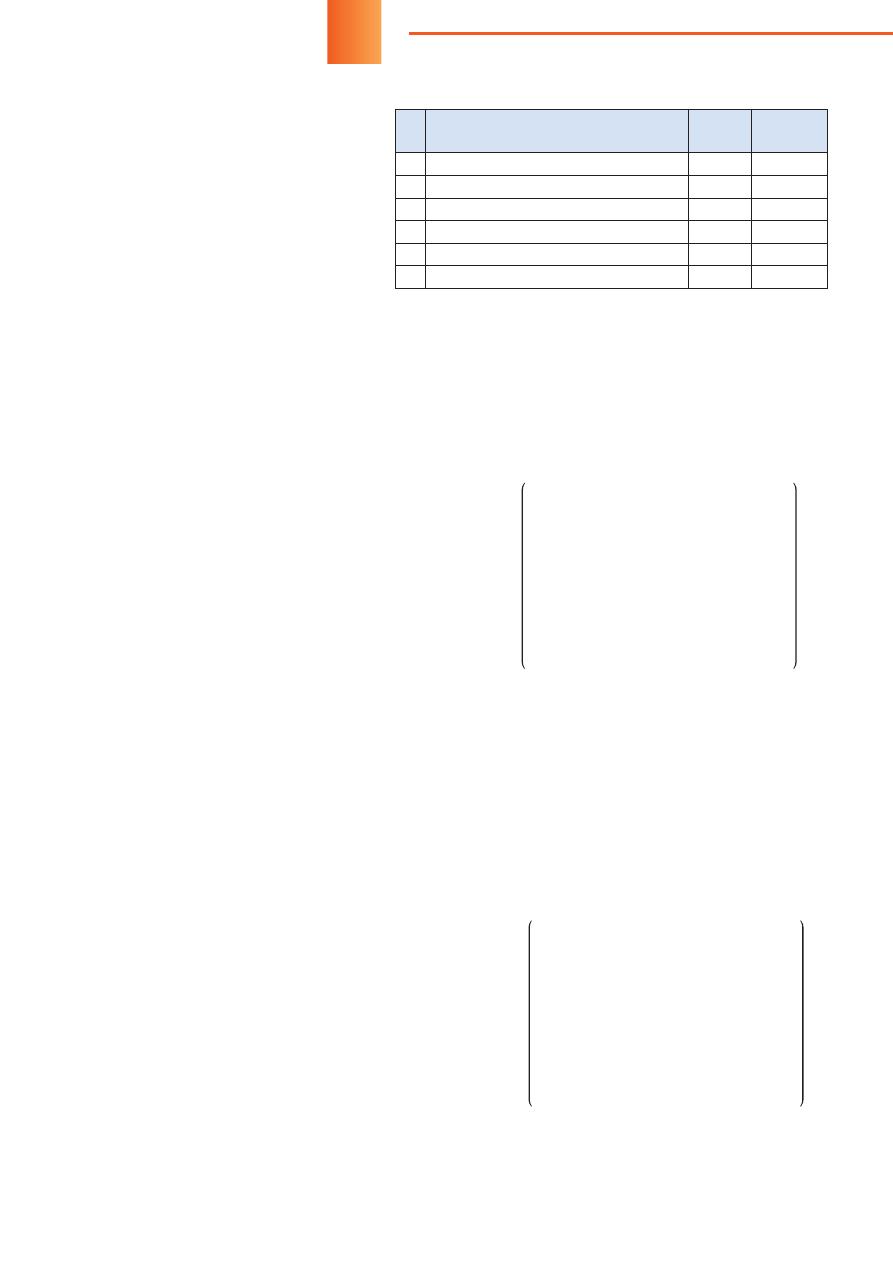
Граф
состояний
системы
РЗ
,
в
котором
реали
-
зованы
описанные
условия
,
представлен
на
ри
-
сунке
1.
В
случайный
момент
времени
происходит
один
из
видов
отказов
(
ложное
срабатывание
,
из
-
лишнее
срабатывание
или
отказ
в
срабатывании
).
Ложное
срабатывание
проявляет
себя
и
приводит
к
отказу
РЗ
(
переход
1
→
4),
что
соответствует
со
-
стоянию
4 —
ложное
срабатывание
.
Время
на
-
хождения
системы
в
состоянии
отказа
составляет
несколько
часов
,
после
чего
следует
восстанов
-
ление
—
переход
в
состояние
9
с
интенсивностью
Л
(
переход
4
→
9).
При
возникновении
дефектов
,
опасных
с
точки
зрения
излишних
срабатываний
,
система
РЗ
переходит
в
неработоспособное
и
не
-
Рис
. 1.
Граф
состояний
и
переходов
системы
релейной
защиты
λ
и
1.Р
2.Ф
и
3.Ф
о
λ
о
4.О
л
λ
л
9.В
μ
в
5.О
и
ν
и
6.О
о
μ
л
ν
о
μ
о
μ
и
8.ПН
7.ПР
λ
п
λ
п
λ
п
μ
п
μ
п
№
6 (39) 2016
112
СЕТИ РОССИИ
заблокированное
состояние
(
переход
1
→
2).
Сам
отказ
—
излишнее
срабаты
-
вание
происходит
только
при
наложении
двух
событий
:
дефекта
и
внешнего
КЗ
с
интенсивностью
И
(
переход
2
→
5).
По
-
сле
отказа
РЗ
следует
восстановление
(
переход
5
→
9).
При
возникновении
де
-
фектов
,
опасных
с
точки
зрения
отказов
в
срабатывании
,
система
РЗ
переходит
в
неработоспособное
и
незаблокирован
-
ное
состояние
(
переход
1
→
3).
Сам
отказ
в
срабатывании
происходит
только
при
наложении
двух
событий
:
дефекта
и
вну
-
треннего
КЗ
с
интенсивностью
О
(
переход
3
→
6).
После
отказа
РЗ
следует
восстановление
(
пере
-
ход
6
→
9).
Исходные
данные
для
численных
расчетов
на
примере
релейной
защиты
воздушной
линии
приве
-
дены
в
таблице
1.
Особенностью
рассматриваемой
системы
явля
-
ется
следующее
обстоятельство
:
время
нахожде
-
ния
в
состояниях
4, 5, 6, 7, 8
является
пренебрежи
-
мо
малым
по
сравнению
со
временем
нахождения
в
состояниях
1, 2, 3.
Поэтому
временем
нахожде
-
ния
в
состояниях
4, 5, 6, 7, 8
можно
пренебречь
.
Теоретически
это
означает
,
что
интенсивность
вы
-
хода
из
этих
состояний
является
бесконечно
боль
-
шой
,
то
есть
П
=
∞
,
И
=
∞
,
О
=
∞
,
Л
=
∞
.
Среднее
время
восстановления
условно
принято
равным
10
часам
.
Итак
,
в
состояниях
2
и
3
система
неработоспособ
-
на
,
в
этих
состояниях
система
находится
конечное
время
.
В
других
неработоспособных
состояниях
,
а
также
в
состояниях
проверки
7
и
8
система
нахо
-
дится
пренебрежимо
малое
время
.
МАТЕМАТИЧЕСКАЯ
МОДЕЛЬ
Представленная
модель
относится
к
классу
аналитических
моделей
,
основанных
на
теории
марковских
процессов
[3, 6–9].
Поскольку
время
нахождения
в
состояниях
4, 5, 6, 7, 8
является
пре
-
небрежимо
малым
(
теоретически
оно
равно
нулю
),
то
после
попадания
в
эти
состояния
имеет
место
«
отражение
»
от
этих
состояний
,
заключающееся
в
мгновенном
переходе
в
другие
состояния
.
Это
об
-
стоятельство
обусловило
выбор
математической
модели
,
а
именно
,
переходы
между
состояниями
описываются
полумарковским
процессом
,
в
кото
-
ром
фиксируются
только
перемены
состояний
.
Пе
-
реходы
между
состояниями
будем
описывать
ве
-
роятностями
p
ij
,
которые
,
в
отличие
от
переходных
вероятностей
цепи
Маркова
,
будем
называть
ве
-
роятностями
прохождений
.
Вероятность
прохож
-
дения
p
ij
—
это
вероятность
того
,
что
произойдет
переход
i
→
j
между
состояниями
i
и
j
при
условии
,
что
происходит
выход
из
состояния
i
[4, 7].
Итак
,
приведенные
предпосылки
позволяют
составить
исходную
модель
функционирования
на
основе
полумарковского
процесса
.
Суммарная
интенсивность
выхода
из
состояний
1, 2, 3:
11
=
П
+
И
+
О
+
K
;
22
=
П
+
И
;
33
=
П
+
О
.
Переходы
из
состояний
1, 2, 3
в
другие
состояния
описываются
вероятностями
прохождений
,
которые
пропорциональны
соответствующим
интенсивнос
-
тям
переходов
:
p
12
=
И
/
11
;
p
13
=
О
/
11
;
p
14
=
Л
/
11
;
p
17
=
П
/
11
;
p
25
=
И
/
11
;
p
28
=
П
/
22
;
p
36
=
О
/
33
;
p
38
=
П
/
33
;.
Матрица
вероятностей
прохождений
между
со
-
стояниями
имеет
вид
:
P
=
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
38
36
28
25
17
14
13
12
p
p
p
p
p
p
p
p
Функционирование
системы
во
времени
удобно
представить
в
виде
циклов
.
Разобьем
множество
со
-
стояний
на
два
подмножества
по
признаку
фаз
экс
-
плуатации
:
U
= {1, 2, 3, 4, 5, 6, 7, 8};
V
= {9}.
В
состояниях
подмножества
U
система
функцио
-
нирует
и
проверяется
,
а
в
состоянии
подмножества
V
она
восстанавливается
.
С
течением
времени
систе
-
ма
находится
в
подмножестве
U
и
после
нахождения
в
этом
подмножестве
переходит
в
подмножество
V
.
Затем
этот
UV
-
цикл
повторяется
.
Выделение
подматриц
вероятностей
прохожде
-
ний
на
подмножествах
U
и
V
:
P
=
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
38
36
28
25
17
14
13
12
p
p
p
p
p
p
p
p
UU
P
VV
= (0).
По
матрицам
P
UU
и
P
VV
вычисляются
матрицы
относительных
частот
N
U
и
N
V
на
подмножествах
U
и
V
[4–5]:
N
U
= ||
n
U
(
i
,
j
) || = (
E
–
P
UU
)
–1
;
N
V
= ||
n
V
(
i
,
j
) || = (
E
–
P
VV
)
–1
,
(1)
Табл
. 1.
Исходные
интенсивности
отказов
№
п
/
п
Наименование
Обозна
-
чение
Значение
,
1/
год
1
Интенсивность
ложных
срабатываний
Л
0,006
2
Интенсивность
излишних
срабатываний
И
0,104
3
Интенсивность
отказов
в
срабатывании
О
0,012
4
Интенсивность
периодической
проверки
П
1–0,1
5
Интенсивность
внешних
КЗ
И
2,7
6
Интенсивность
внутренних
КЗ
О
2,45
113
где
E
—
единичная
матрица
соответствующего
по
-
рядка
,
n
U
(
i
,
j
) —
средняя
относительная
частота
j
-
го
состояния
,
или
математическое
ожидание
числа
вхождений
в
j
-
е
состояние
до
выхода
из
подмноже
-
ства
U
при
условии
,
что
i
-
е
состояние
этого
подмно
-
жества
является
начальным
.
Относительной
частоте
придается
следующий
смысл
:
n
U
(
i
,
j
) —
это
математическое
ожидание
чис
-
ла
вхождений
(
попаданий
)
в
j
-
е
состояние
до
выхо
-
да
из
подмножества
U
,
приходящееся
на
одно
вос
-
становление
.
Поскольку
состояние
1
при
переходе
V
→
U
всегда
является
начальным
,
то
относительные
частоты
состояний
подмножества
U
описываются
только
первой
строкой
матрицы
N
U
.
Первая
строка
матрицы
N
U
имеет
вид
:
n
1
= ||
n
U
(1,
j
) || =
1
И
·
И
О
·
О
И
О
= —
11
И
О
Л
— —
П
П
— + — .(2)
П
+
Л
+
о
22
33
22
33
Очевидно
,
что
N
V
= (1).
Для
получения
временных
характеристик
состо
-
яний
и
подмножеств
состояний
вводится
матрица
средних
времен
нахождения
в
состояниях
подмно
-
жества
U
при
однократном
попадании
в
состояния
:
Θ
U
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
λ
/
1
0
0
0
0
0
0
0
0
λ
/
1
0
0
0
0
0
0
0
0
λ
/
1
33
22
11
=
Тогда
строка
средних
времен
нахождения
в
состо
-
яниях
подмножеств
U
и
V
на
одном
цикле
имеют
вид
:
t
U
= ||
t
U
(1,
j
) || =
n
1
U
=
1
И
О
=
— 1 — — 0 0 0 0 0 . (3)
П
+
Л
+
о
И
+
Л
О
+
П
Элемент
t
U
(
1
,
j
) —
это
среднее
время
нахождения
в
j
-
м
состоянии
,
приходящееся
на
одно
восстановле
-
ние
.
Теперь
можно
получить
формулу
для
среднего
времени
нахождения
в
подмножестве
U:
И
+
П
) ·
О
+
П
) +
И
·
О
+
П
) +
О
·
И
+
П
)
t
U
=
t
U
ė
= ——, (4)
И
+
П
) ·
О
+
П
) ·
И
+
Л
+
о
)
где
ė
—
столбец
,
все
элементы
которого
равны
1.
Среднее
время
UV
-
цикла
составляет
t
UV
=
t
U
+
t
V
=
И
+
П
) ·
О
+
П
) +
И
·
О
+
П
) +
О
·
И
+
П
)
=
—— +
t
В
, (5)
И
+
П
) ·
О
+
П
) ·
И
+
Л
+
о
)
где
t
В
—
принятое
среднее
время
восстановления
системы
РЗ
от
2
до
10
часов
в
соответствии
с
экс
-
плуатационной
документацией
РЗ
.
Средняя
частота
цикла
,
имеющая
смысл
средне
-
го
числа
восстановлений
в
единицу
времени
(
в
дан
-
ном
случае
за
один
год
),
вычисляется
по
формуле
:
UV
= 1 /
t
UV
. (6)
Среднее
суммарное
время
нахождения
в
нерабо
-
тоспособных
состояниях
2
и
3
на
одном
UV
-
цикле
:
t
Н
=
t
U
(1,2) +
t
U
(1,3) =
И
·
О
+
П
) +
О
·
И
+
П
)
=
—— .
(7)
И
+
П
) ·
О
+
П
) ·
И
+
Л
+
о
)
Коэффициент
неготовности
,
вычисленный
в
соот
-
ветствии
с
[1]:
t
Н
t
Н
/
t
U
K
Н
= — = — .
(8)
t
UV
1 +
t
В
/
t
U
t
Н
И
·
О
+
П
) +
О
·
И
+
П
)
где
— = ——; (9)
t
U
И
+
П
) ·
О
+
П
) +
И
·
О
+
П
) +
О
·
И
+
П
)
t
В
И
+
П
) ·
О
+
П
) ·
И
+
Л
+
о
) ·
t
В
— = ——; (10)
t
U
И
+
П
) ·
О
+
П
) +
И
·
О
+
П
) +
О
·
И
+
П
)
Как
отмечено
ранее
,
для
данного
примера
сред
-
нее
время
восстановления
системы
РЗ
принято
10
часов
.
Среднее
число
проверок
на
одном
цикле
составляет
n
П
=
n
U
(1,7) +
n
U
(1,8) =
П
И
О
=
— · 1 + — + — .
(11)
П
+
Л
+
о
П
+
И
П
+
О
Средняя
частота
проверок
,
то
есть
среднее
число
проверок
в
течение
года
составляет
П
=
n
П
·
UV
. (12)
Среднее
время
между
проверками
t
П
и
соответ
-
ственно
интенсивность
проверок
П
являются
пара
-
метрами
,
которые
можно
устанавливать
в
процессе
эксплуатации
.
В
таблице
2
приведена
зависимость
от
этих
параметров
среднего
времени
цикла
t
UV
,
средней
частоты
цикла
UV
,
коэффициента
неготов
-
ности
Кн
,
среднего
числа
проверок
на
одном
цикле
n
П
и
средней
частоты
проверок
П
.
Из
таблицы
2
видно
,
что
при
изменении
уста
-
новленных
параметров
(
t
П
и
П
)
в
120
раз
частота
проверок
не
изменяется
,
а
частота
восстановлений
изменяется
незначительно
,
в
пределах
3,5%.
Это
обусловлено
тем
,
что
переходы
в
состояние
восста
-
новления
определяются
внешними
и
внутренними
КЗ
с
большими
значениями
интенсивностей
.
Однако
коэффициент
неготовности
изменяется
существен
-
но
:
от
0,008
при
большой
интенсивности
проверок
до
0,042
при
отсутствии
периодической
проверки
(
П
= 0),
то
есть
коэффициент
неготовности
возрас
-
тет
на
80%
по
отношению
к
случаю
,
когда
проверок
Табл
. 2.
Значения
показателей
эксплуатации
и
надежности
при
разных
значениях
среднего
времени
между
проверками
t
П
(
год
)
П
(1/
год
)
t
UV
(
год
)
UV
(1/
год
)
K
Н
n
П
П
(1/
год
)
1/12
12
8,263
0,121
0,008
4,248
0,083
0,25
4
8,340
0,120
0,017
4,248
0,083
0,5
2
8,401
0,119
0,024
4,248
0,083
1
1
8,457
0,118
0,031
4,248
0,083
2
0,5
8,498
0,118
0,035
4,248
0,083
3
0,333
8,514
0,117
0,037
4,248
0,083
4
0,25
8,523
0,117
0,038
4,248
0,083
5
0,2
8,529
0,117
0,039
4,248
0,083
6
0,167
8,533
0,117
0,039
4,248
0,083
7
0,143
8,536
0,117
0,040
4,248
0,083
8
0,125
8,538
0,117
0,040
4,248
0,083
9
0,111
8,538
0,117
0,040
4,248
0,083
10
0,1
8,541
0,117
0,040
4,248
0,083
∞
0
8,554
0,117
0,042
4,248
0,083
№
6 (39) 2016
114
СЕТИ РОССИИ
не
проводится
.
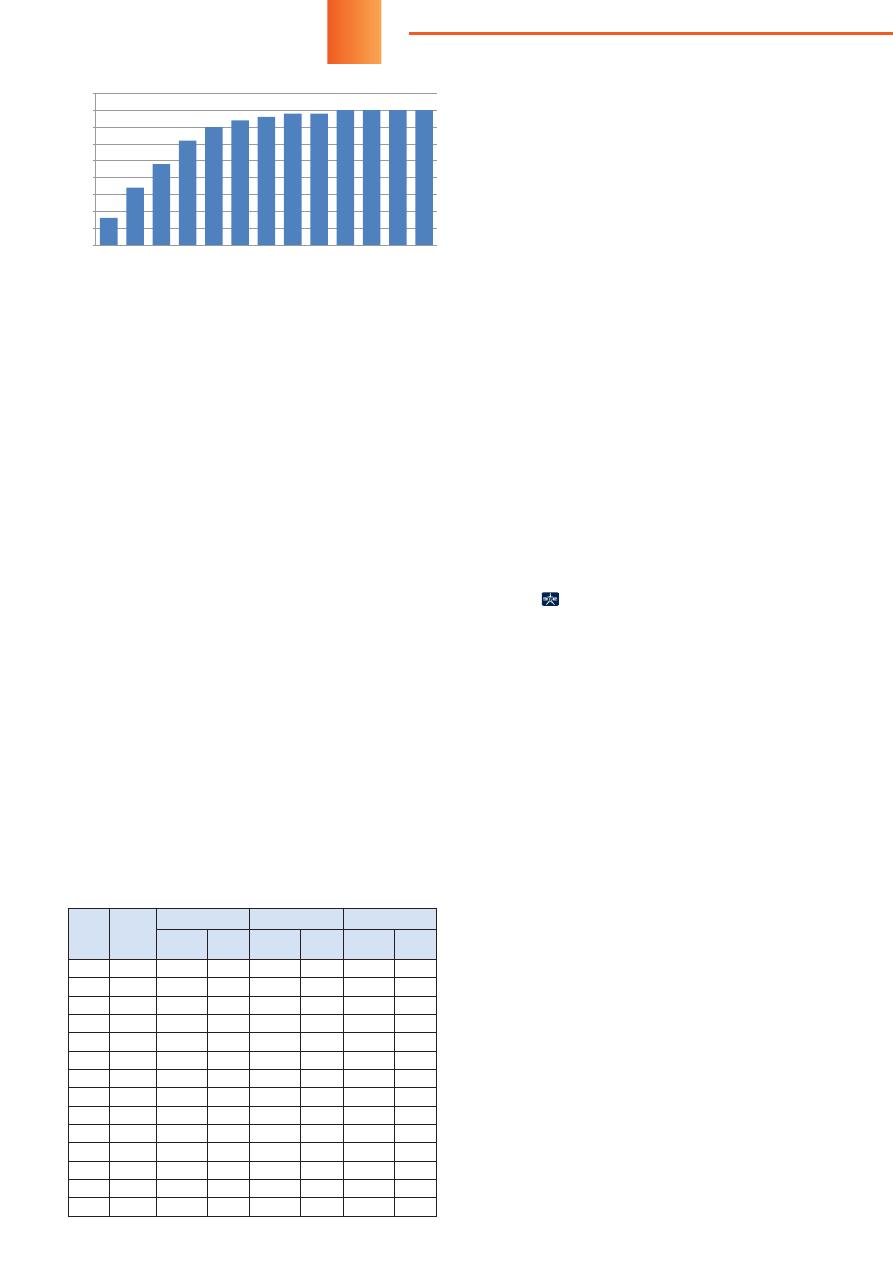
Зависимость
коэффициента
неготов
-
ности
системы
РЗ
K
Н
от
среднего
времени
между
проверками
t
П
приведена
на
рисунке
2.
В
соответствии
со
сложившимися
традициями
в
области
энергетики
,
следует
учесть
потери
,
связан
-
ные
с
возникновением
и
устранением
отказов
разного
типа
.
Для
этой
цели
найдем
вероятностные
характе
-
ристики
состояний
4, 5, 6,
а
именно
n
U
(1,
j
) —
сред
-
нее
число
переходов
в
j
-
е
состояние
на
одном
цикле
и
j
—
среднюю
частоту
j
-
го
состояния
:
П
n
U
(1,4) = — ;
4
=
n
U
(1,4) ·
UV
; (13)
П
+
Л
+
о
П
·
И
n
U
(1,5) = — ;
5
=
n
U
(1,5) ·
UV
; (14)
П
+
Л
+
о
) ·
П
+
И
)
О
·
О
n
U
(1,6) = — ;
5
=
n
U
(1,6) ·
UV
; (15)
П
+
Л
+
о
) ·
П
+
О
)
Эти
характеристики
при
разных
значениях
t
П
и
П
приведены
в
таблице
3.
Из
таблицы
следует
,
что
ча
-
стота
отказов
вида
«
ложное
срабатывание
»
не
за
-
висит
от
установленной
периодичности
проверок
,
однако
частоты
отказов
вида
«
излишнее
срабатыва
-
ние
»
и
«
отказ
в
срабатывании
»
существенно
изме
-
няются
:
возрастают
примерно
в
5
раз
при
отсутствии
периодической
проверки
(
П
= 0).
Суммарная
часто
-
та
отказов
РЗ
находится
путем
суммирования
частот
отказов
всех
типов
:
S
=
4
+
5
+
6
.
Вклад
отказа
каждого
вида
можно
оценить
по
его
частоте
относи
-
тельно
суммарной
частоты
отказов
:
Л
=
4
/
S
,
И
=
5
/
S
,
О
=
6
/
S
.
При
самой
большой
интенсивности
проверок
П
= 12/
год
:
Л
= 22%,
И
= 70%,
О
= 8%.
При
от
-
сутствии
периодической
проверки
(
П
= 0):
Л
= 5%,
И
= 85%,
О
= 10%.
Видно
,
что
самый
большой
вклад
по
частоте
отказов
вносят
отказы
вида
«
излишнее
срабатывание
» (70–85%),
а
на
остальные
типы
от
-
казов
приходится
15–30%.
ЗАКЛЮЧЕНИЕ
Разработана
модель
цикла
функционирования
си
-
стемы
РЗ
воздушной
линии
на
основе
теории
полу
-
марковских
процессов
.
Модель
позволяет
рассчитать
и
спрогнозировать
ряд
показателей
эксплуатации
и
надежности
,
таких
как
коэффициент
неготовности
,
частота
восстановления
,
частота
проверок
техниче
-
ского
состояния
системы
РЗ
.
Приведенная
модель
позволила
учесть
три
разных
вида
отказов
и
получить
частоты
этих
отказов
.
На
ее
основе
можно
выявить
факторы
,
влияющие
на
надеж
-
ность
системы
РЗ
,
и
оценить
зависимость
коэффици
-
ента
неготовности
от
различных
влияющих
факторов
.
Достоинством
модели
является
возможность
ее
реа
-
лизации
средствами
компьютерного
моделирования
на
основе
таких
систем
,
как
Mathcad
или
Matlab.
Приведенная
модель
позволяет
рассчитать
доста
-
точно
широкий
ряд
показателей
эксплуатации
и
на
-
дежности
,
которые
могут
быть
использованы
при
ис
-
следовании
на
этапе
проектирования
и
модернизации
систем
РЗ
.
ЛИТЕРАТУРА
1.
ГОСТ
Р
53480–2009.
Надежность
в
технике
.
Тер
-
мины
и
определения
.
2.
Гук
Ю
.
Б
.
Анализ
надежности
электроэнергетиче
-
ских
установок
.
Л
.:
Энергоатомиздат
, 1988. 224
с
.
3.
Зеленцов
Б
.
П
.
Аналитическое
моделирование
сложных
вероятностных
систем
//
Моделирование
информационных
сетей
.
Труды
Вычислительного
центра
СО
РАН
.
Серия
:
Информатика
,
вып
. 1.
Но
-
восибирск
, 1994.
С
. 144–152.
4.
Зеленцов
Б
.
П
.
Матричные
модели
надежности
си
-
стем
:
инженерные
методы
расчета
.
Новосибирск
:
Наука
, 1991. 112
с
.
5.
Зеленцов
Б
.
П
.,
Максимов
В
.
П
.,
Шувалов
В
.
П
.
Мо
-
дель
функционирования
линии
связи
в
условиях
недостоверного
контроля
технического
состояния
.
Вестник
СибГУТИ
, 2015,
№
3.
6.
Кельберт
М
.
Я
.,
Сухов
Ю
.
М
.
Вероятность
и
ста
-
тистика
в
примерах
и
задачах
.
Т
. 2.
М
.:
МЦНМО
,
2010.
7.
Королюк
В
.
С
.
и
др
.
Полумарковские
процессы
и
их
приложения
.
Киев
, 1970.
8.
Надежность
технических
систем
:
Справочник
/
Ю
.
К
.
Беляев
,
В
.
А
.
Богатырев
,
В
.
В
.
Болотин
и
др
.
Под
ред
.
И
.
А
.
Ушакова
.
Радио
и
связь
, 1985. 608
с
.
9.
Самарский
А
.
А
.
Математическое
моделирование
.
М
.:
Физматлит
, 2002. 320
с
.
10.
Смирнов
Э
.
П
.
Влияние
профилактического
контро
-
ля
на
результирующую
надежность
релейной
за
-
щиты
//
Электричество
, 1968,
№
4.
С
. 10–15.
11.
Шалин
А
.
И
.
Надежность
и
диагностика
релейной
защиты
энергосистем
.
Новосибирск
:
Изд
-
во
НГТУ
,
2003. 384
с
.
0
0,005
0,01
0,015
0,02
0,025
0,03
0,035
0,04
0,045
0,08
0,25
0,5
1
2
3
4
5
6
7
8
9
10
K
Н
t
П
,
год
Рис
. 2.
Изменение
коэффициента
неготовности
систе
-
мы
РЗ
К
Н
от
среднего
времени
между
проверками
t
П
Табл
. 3.
Вероятностные
характеристики
состояний
4, 5, 6
t
П
П
Состояние
4
Состояние
5
Состояние
6
n
U
(1,4)
4
n
U
(1,5)
5
n
U
(1,6)
6
1/12
12
0,049
0,006
0,157
0,019
0,017
0,002
0,25
4
0,049
0,006
0,344
0,041
0,037
0,004
0,5
2
0,049
0,006
0,490
0,058
0,054
0,006
1
1
0,049
0,006
0,622
0,074
0,070
0,008
2
0,5
0,049
0,006
0,719
0,085
0,082
0,010
3
0,333
0,049
0,006
0,759
0,089
0,087
0,010
4
0,25
0,049
0,006
0,780
0,092
0,089
0,010
5
0,2
0,049
0,006
0,794
0,093
0,091
0,011
6
0,167
0,049
0,006
0,803
0,094
0,092
0,011
7
0,143
0,049
0,006
0,810
0,095
0,093
0,011
8
0,125
0,049
0,006
0,815
0,095
0,094
0,011
9
0,111
0,049
0,006
0,819
0,096
0,094
0,011
10
0,1
0,049
0,006
0,822
0,096
0,095
0,011
∞
0
0,049
0,006
0,852
0,100
0,098
0,011
Оригинал статьи: Модель функционирования релейной защиты энергосистем
В статье приведена аналитическая модель функционирования релейной защиты энергосистем, в которой учтены три группы отказов и проверки работоспособности. Модель основана на описании процесса функционирования полумарковским процессом. С помощью этой модели получены такие показатели эксплуатации и надёжности, как коэффициент неготовности, средняя частота восстановлений, частоты неработоспособных состояний.