Методика формирования математической модели ЭЭС для расчетов несинусоидальных установившихся режимов и исследования резонансных явлений. Часть 1. Алгоритм методики и практические аспекты моделирования

54

КАЧЕСТВО 

ЭЛЕКТРОЭНЕРГИИ

Методика формирования математической 
модели ЭЭС для расчетов несинусоидальных 
установившихся режимов и исследования 
резонансных явлений. Часть 1. Алгоритм 
методики и практические аспекты 
моделирования

УДК

 621.316.7:004.942

Характерной

проблемой

для

ЭЭС

, 

в

составе

которых

функционируют

мощные

электро

-

приемники

с

нелинейной

вольт

-

амперной

характеристикой

, 

является

массовое

и

систе

-

матическое

невыполнение

требований

к

допустимым

гармоническим

искажениям

на

-

пряжения

, 

в

том

числе

в

питающих

сетях

 110 

кВ

и

выше

. 

В

то

же

время

существующие

практические

подходы

к

моделированию

ЭЭС

на

частотах

высших

гармоник

являются

сильно

упрощенными

и

позволяют

получить

лишь

грубые

оценки

резонансных

частот

и

ожидаемых

значений

коэффициентов

n

-

х

гармоник

тока

и

напряжения

, 

что

существен

-

но

снижает

эффективность

разрабатываемых

мероприятий

по

нормализации

качества

электроэнергии

. 

Для

исключения

указанного

риска

предложена

методика

формиро

-

вания

математической

модели

ЭЭС

для

расчетов

несинусоидальных

установившихся

режимов

и

исследования

резонансных

явлений

.

О

беспечение

качества

элек

-

трической

энергии

  (

КЭ

) 

яв

-

ляется

одной

из

важнейших

задач

в

условиях

рыночной

модели

экономических

отношений

в

электроэнергетике

, 

необходимость

решения

которой

продиктована

по

-

ложениями

действующего

законода

-

тельства

 [1, 2]. 

Важной

характеристи

-

кой

КЭ

является

степень

искажения

синусоидальности

кривой

напряже

-

ния

, 

определяемая

в

соответствии

с

ГОСТ

 32144-2013 [3] 

значениями

суммарного

коэффициента

гармони

-

ческих

составляющих

K

U

и

коэффи

-

циентов

n

-

х

гармонических

составля

-

ющих

K

U

(

n

)

.

Представленный

в

монографии

 [4] 

анализ

результатов

измерений

пока

-

зателей

КЭ

, 

проведенных

в

послед

-

ние

годы

на

электросетевых

объ

-

ектах

 0,4–220 

кВ

, 

показывает

, 

что

в

районах

концентрации

потребите

-

лей

, 

в

составе

которых

функциониру

-

ют

электроприемники

с

нелинейной

вольт

-

амперной

характеристикой

 (

да

-

лее

 — 

нелинейные

нагрузки

), 

к

числу

которых

относятся

предприятия

чер

-

ной

и

цветной

металлургии

, 

нефтедо

-

бывающей

промышленности

, 

а

также

электрифицированная

тяга

, 

харак

-

терны

систематические

превышения

допустимых

значений

K

U

и

K

U

(

n

)

. 

При

этом

для

электрических

сетей

напря

-

жением

 110 

кВ

и

выше

ЕЭС

России

характерна

сложнозамкнутая

струк

-

тура

, 

значительная

единичная

про

-

тяженность

ЛЭП

и

изменение

режим

-

ных

параметров

в

широких

пределах

, 

что

оказывает

сильное

влияние

на

уровни

высших

гармоник

 (

ВГ

) 

напря

-

жения

и

их

распространение

.

В

условиях

отсутствия

широко

-

масштабных

систем

мониторинга

КЭ

в

отечественном

электросетевом

ком

-

плексе

возможность

получить

расчет

-

ные

оценки

указанных

показателей

с

применением

любой

доступной

ин

-

формации

является

критически

важ

-

ной

для

решения

как

проектных

, 

так

и

эксплуатационных

задач

. 

Однако

методические

документы

, 

регламен

-

тирующие

состав

необходимых

рас

-

четов

и

требования

к

их

выполнению

, 

в

настоящее

время

отсутствуют

 [5]. 

Не

регламентирован

также

и

про

-

цесс

формирования

математических

моделей

ЭЭС

, 

являющихся

основой

для

проведения

подобных

расчетов

: 

на

сегодняшний

день

в

ряде

источни

-

ков

 [6–9] 

содержатся

разрозненные

и

крайне

обобщенные

рекомендации

по

их

разработке

. 

С

учетом

описанных

предпосылок

в

настоящей

статье

идентифициро

-

ваны

основные

недостатки

наиболее

Солодовников

В

.

Е

., 

руководитель

проектов

ООО

 «

ЭТС

-

Энерго

»

Флёров

А

.

Н

., 

инженер

ведущий

отдела

метрологии

и

контроля

качества

электрической

энергии

АО

 «

Россети

Тюмень

»

Тульский

В

.

Н

., 

к

.

т

.

н

., 

доцент

, 

директор

института

электроэнергетики

ФГБОУ

ВО

 «

НИУ

 «

МЭИ

»

Шамонов

Р

.

Г

.,

к

.

т

.

н

., 

начальник

управления

сопровождения

ОТУ

и

режимов

Департамента

оперативно

-

технологического

управления

ПАО

 «

Россети

»

Королев

А

.

А

.,

к

.

т

.

н

., 

профессор

кафедры

«

Электроэнергетика

транспорта

» 

ФГАОУ

ВО

РУТ

(

МИИТ

)

Ключевые

слова

: 

качество

электроэнергии

, 

высшие

гармоники

, 

гармонические

искажения

токов

и

напряжений

, 

резонанс

, 

режимы

энергосистем

, 

моделирование

энергосистем

55

часто

применяемого

на

практике

подхода

к

форми

-

рованию

модели

ЭЭС

на

частотах

высших

гармоник

(

ВГ

) 

и

предложена

методика

формирования

матема

-

тической

модели

ЭЭС

для

расчетов

несинусоидаль

-

ных

установившихся

режимов

  (

УР

) 

и

исследования

частотных

характеристик

  (

ЧХ

) 

входных

сопротивле

-

ний

относительно

узлов

по

прямой

и

обратной

по

-

следовательностям

.

ОБЩИЕ

ПОЛОЖЕНИЯ

Одним

из

основных

требований

, 

предъявляемых

к

математической

модели

ЭЭС

, 

является

ее

уни

-

версальность

для

проведения

расчетов

УР

на

ос

-

новной

частоте

и

на

частотах

ВГ

, 

а

также

расчетов

для

идентификации

резонансных

частот

, 

с

приме

-

нением

современных

промышленных

программно

-

вычислительных

комплексов

  (

ПВК

). 

При

выполне

-

нии

данного

условия

модель

принципиально

может

быть

сформирована

на

основе

существующей

мо

-

дели

ЭЭС

для

расчетов

УР

на

основной

частоте

, 

что

позволяет

:

– 

уменьшить

трудоемкость

решения

задачи

по

-

средством

совмещения

расчетов

УР

ЭЭС

на

ос

-

новной

частоте

, 

частотах

ВГ

, 

а

также

ЧХ

входных

сопротивлений

относительно

узлов

в

едином

вы

-

числительном

процессе

;

– 

упростить

процессы

сопровождения

и

практиче

-

ского

применения

математической

модели

ЭЭС

.

В

современных

ПВК

расчет

несинусоидальных

УР

ЭЭС

в

подавляющем

большинстве

случаев

произво

-

дится

по

методу

harmonic penetration

 («

проникание

гармоник

»)

1

. 

Основным

допущением

данного

метода

является

отсутствие

зависимости

эмиссии

ВГ

тока

нелинейными

элементами

от

спектрального

состава

напряжений

в

точках

их

присоединения

 [6, 7, 10], 

что

равносильно

представлению

нелинейной

электриче

-

ской

цепи

в

виде

условно

линейной

на

частотах

ВГ

, 

входящих

в

рассматриваемый

диапазон

2

 [11]. 

Тогда

в

соответствии

с

теоремами

Нортона

и

Тевенена

не

-

линейные

элементы

в

расчетной

схеме

могут

быть

представлены

в

виде

эквивалентных

неидеальных

источников

тока

или

ЭДС

, 

параметры

которых

за

-

висят

от

порядка

гармоники

 [6, 7, 10–12]. 

Следова

-

тельно

, 

УР

электрической

цепи

на

частотах

ВГ

мо

-

жет

быть

описан

системой

линейных

алгебраических

уравнений

, 

и

расчет

на

частоте

каждой

гармоники

может

быть

проведен

независимо

 [6, 7].

При

выражении

токов

и

ЭДС

эквивалентных

ис

-

точников

в

процентах

от

соответствующих

режимных

параметров

на

основной

частоте

расчеты

УР

во

всем

анализируемом

частотном

диапазоне

могут

быть

вы

-

полнены

в

едином

вычислительном

процессе

. 

Расчет

УР

ЭЭС

на

основной

частоте

обычно

производится

методами

решения

систем

нелинейных

алгебраиче

-

ских

уравнений

, 

а

на

частотах

ВГ

 — 

линейных

урав

-

нений

, 

согласно

выражению

:

Y

(

n

)

∙

U

(

n

)

 = 

I

(

n

)

, (1)

где

Y

(

n

)

 — 

матрица

узловых

проводимостей

на

ча

-

стоте

n

-

й

гармоники

; 

U

(

n

)

и

I

(

n

)

 — 

векторы

-

столбцы

узловых

напряжений

и

токов

в

узлах

на

частоте

n

-

й

гармоники

.

Равенство

 (1) 

является

также

основой

для

метода

анализа

частотных

характеристик

ЭЭС

, 

называемо

-

го

frequency scan

 («

частотное

сканирование

»). 

Если

для

узла

i

на

частоте

гармоники

n

принять

, 

что

узло

-

вой

ток

İ

(

n

)

i

 = 1



0 

А

, 

а

все

остальные

узловые

токи

принять

равными

нулю

, 

то

расчетное

значение

U

̇

(

n

)

i

в

вольтах

будет

численно

равно

входному

сопротив

-

лению

относительно

данного

узла

Ż

вх

(

n

)

i

. 

Результатом

серии

расчетов

при

последовательном

увеличении

частоты

будет

годограф

Ż

вх

i

, 

при

этом

частотная

за

-

висимость

его

модуля

будет

выражать

амплитудно

-

частотную

характеристику

  (

АЧХ

), 

а

угла

 — 

фазо

-

частотную

характеристику

  (

ФЧХ

). 

Абсциссы

нулей

ФЧХ

соответствуют

резонансным

частотам

 [11].

При

проведении

расчетов

УР

и

ЧХ

в

отношении

гармоник

, 

образующих

системы

трехфазных

токов

и

напряжений

прямой

и

обратной

последователь

-

ностей

, 

математическая

модель

ЭЭС

может

быть

значительно

упрощена

, 

поскольку

в

таком

случае

па

-

раметры

схем

замещения

всех

ее

элементов

опреде

-

ляются

единообразно

:

– 

для

элементов

, 

представляющих

собой

непод

-

вижные

друг

относительно

друга

магнитосвязан

-

ные

цепи

, 

сопротивления

прямой

и

обратной

по

-

следовательности

равны

 [13];

– 

вращающиеся

электрические

машины

на

часто

-

те

n

-

й

гармоники

обычно

представляются

пас

-

сивными

активно

-

индуктивными

шунтами

вида

Ż

(

n

)

 = 

k

R

(

n

)

R

 + 

jnX

, 

где

k

R

(

n

)

 — 

поправочный

коэф

-

фициент

, 

учитывающий

увеличение

активного

со

-

противления

вследствие

поверхностного

эффек

-

та

3

 [6–8, 10, 12].

В

качестве

дополнительного

допущения

обычно

принимается

равенство

по

фазам

схемных

и

режим

-

ных

параметров

ЭЭС

во

всем

анализируемом

частот

-

ном

диапазоне

, 

что

позволяет

формировать

матема

-

тическую

модель

для

расчетов

несинусоидальных

УР

в

однофазном

эквиваленте

и

непосредственно

на

основе

модели

для

расчетов

УР

на

основной

часто

-

те

, 

что

соответствует

исходному

требованию

к

уни

-

версальности

 [6–8, 14]. 

Несимметрия

режимных

па

-

раметров

при

проведении

расчетов

на

частотах

ВГ

обычно

учитывается

путем

задания

в

модели

ЭЭС

максимальных

для

трех

фаз

значений

токов

и

ЭДС

эквивалентных

источников

, 

что

соответствует

наибо

-

лее

тяжелым

расчетным

условиям

 [6, 8].

1

Согласно

обзору

в

 [6, 10]. 

К

числу

таких

ПВК

относятся

, 

например

, ETAP 

и

 DIgSILENT PowerFactory.

2

Допущение

является

достаточно

грубым

с

точки

зрения

теории

электрических

цепей

, 

однако

метод

дает

приемлемые

резуль

-

таты

применительно

к

ЭЭС

 [6].

3

Для

синхронных

машин

 R 

и

 X 

соответствуют

активной

и

индуктивной

составляющей

сопротивления

обратной

последователь

-

ности

, 

для

асинхронных

 — 

сопротивления

короткого

замыкания

. 

Методы

расчета

k

R

(

n

)

подробно

изложены

в

 [6–8, 10, 14], 

анало

-

гичная

поправка

при

необходимости

может

вводиться

и

в

отношении

индуктивных

сопротивлений

 [8, 12]. 

Электрические

машины

обычно

рассматриваются

как

источники

гармоник

только

применительно

к

изолированным

ЭЭС

с

соизмеримыми

мощностями

генераторов

и

двигателей

 [15].

№

 4 (79) 2023

56

КАЧЕСТВО 

ЭЛЕКТРОЭНЕРГИИ

Важно

отметить

, 

что

расчеты

УР

ЭЭС

на

частотах

гармоник

, 

кратных

трем

, 

также

производятся

с

уче

-

том

описанных

выше

допущений

, 

но

с

применением

математической

модели

по

нулевой

последователь

-

ности

, 

обычно

формируемой

для

расчетов

несиммет

-

ричных

коротких

замыканий

.

Приведенные

далее

предложения

, 

касающие

-

ся

порядка

формирования

математической

модели

ЭЭС

для

расчета

несинусоидальных

УР

и

исследо

-

вания

ее

частотных

свойств

, 

сформулированы

в

от

-

ношении

величин

по

прямой

 (

обратной

) 

последова

-

тельности

.

НЕДОСТАТКИ

СУЩЕСТВУЮЩЕГО

ПОДХОДА

К

ИССЛЕДОВАНИЮ

НЕСИНУСОИДАЛЬНЫХ

УР

И

ЧАСТОТНЫХ

СВОЙСТВ

ЭЭС

В

учебной

и

методической

литературе

 [10, 12, 16–18] 

изложен

упрощенный

подход

, 

ограниченно

приме

-

нимый

для

распределительных

сетей

напряжением

6–35 

кВ

, 

в

соответствии

с

которым

при

проведении

расчетов

несинусоидальных

УР

вся

ЭЭС

, 

за

исклю

-

чением

рассматриваемого

фрагмента

распредели

-

тельной

сети

, 

представляется

эквивалентным

источ

-

ником

ЭДС

, 

внутреннее

сопротивление

которого

на

частоте

n

-

й

гармоники

определяется

по

выражению

:

X

ЭЭС

(

n

)

 = 

n

∙

X

кз

, (2)

где

X

кз

 — 

индуктивное

сопротивление

короткого

за

-

мыкания

 (

КЗ

), 

вычисляемое

по

известному

значению

тока

трехфазного

КЗ

на

шинах

ВН

центра

питания

110 

кВ

и

выше

.

В

указанных

источниках

особо

отмечено

, 

что

при

подобном

представлении

не

учитывается

сложная

частотная

зависимость

эквивалентного

сопротивле

-

ния

ЭЭС

, 

обусловленная

функционированием

эле

-

ментов

с

емкостной

проводимостью

, 

в

связи

с

чем

получаемые

расчетные

уровни

K

U

(

n

)

в

точках

рас

-

пределительной

сети

и

на

шинах

питающего

центра

следует

рассматривать

как

весьма

приблизительную

оценку

. 

Однако

простота

данного

подхода

обуслови

-

ла

настолько

широкое

его

применение

, 

что

он

нашел

отражение

даже

в

нормативных

документах

 — 

так

, 

стандарты

 [19, 20] 

предписывают

для

оценки

до

-

пустимости

условий

работы

БСК

напряжением

до

1000 

В

и

свыше

 1000 

В

определять

резонансные

ча

-

стоты

, 

исходя

из

значения

X

кз

в

точке

их

присоеди

-

нения

.

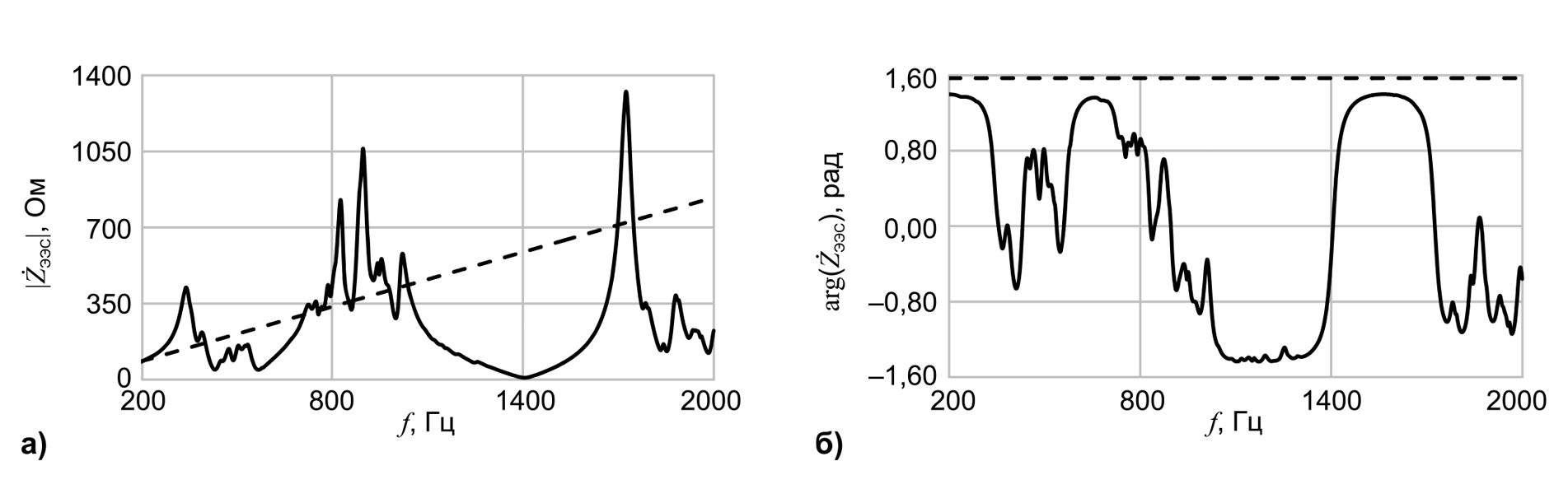
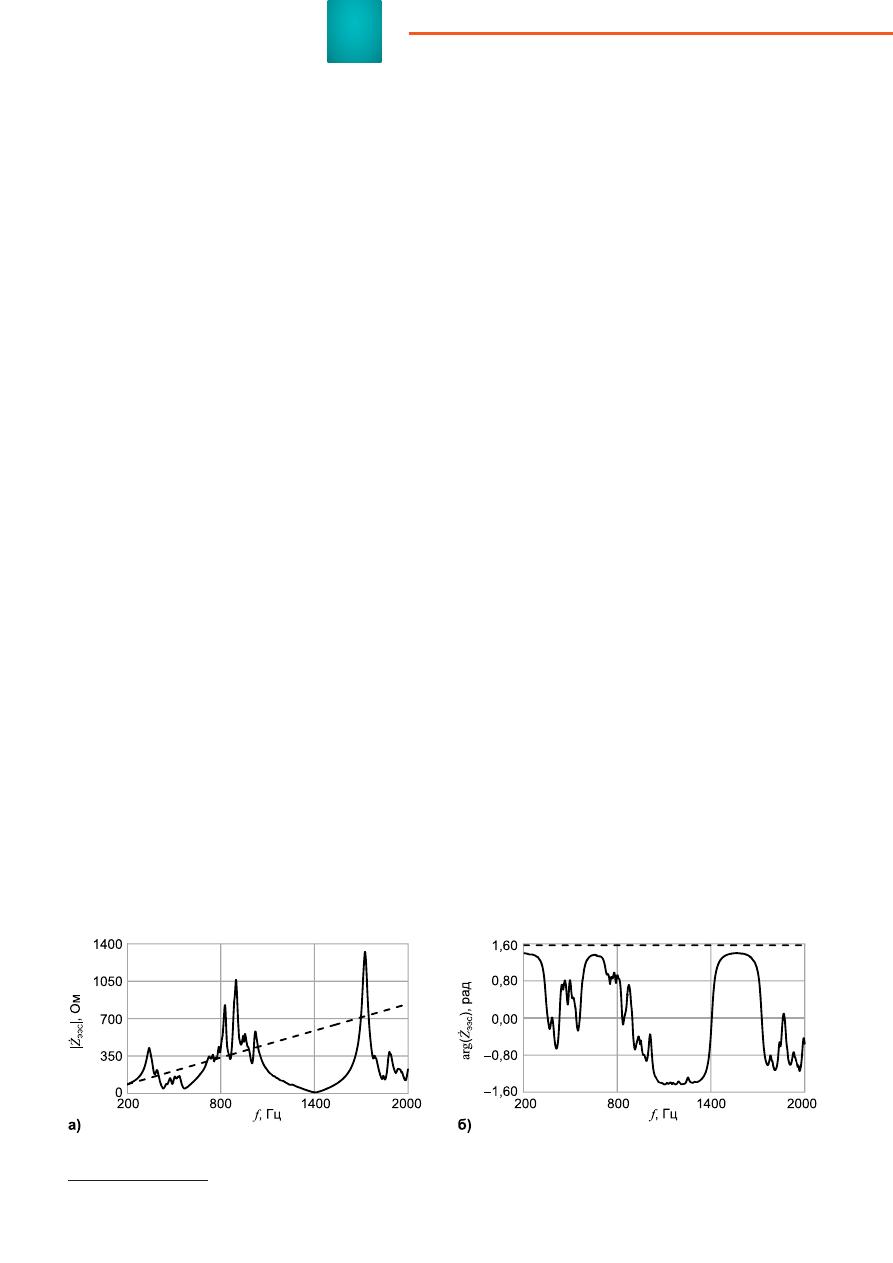
Очевидную

некорректность

указанного

подхода

иллюстрируют

графики

АЧХ

и

ФЧХ

эквивалентного

сопротивления

ЭЭС

относительно

шин

 110 

кВ

одно

-

го

из

питающих

центров

, 

приведенные

на

рисунке

 1. 

Пунктиром

на

графике

изображены

ЧХ

, 

соответству

-

ющие

упрощенному

подходу

, 

а

сплошной

линией

 — 

зависимости

, 

полученные

с

использованием

подроб

-

ной

математической

модели

ЭЭС

.

Из

рисунка

 1 

видно

, 

что

в

рассматриваемом

диапазоне

частот

сопротивление

может

иметь

как

активно

-

индуктивный

, 

так

и

активно

-

емкостный

ха

-

рактер

, 

в

то

время

как

при

упрощенном

представле

-

нии

ЭЭС

данные

особенности

не

учитываются

.

Следует

дополнительно

отметить

, 

что

упрощен

-

ный

подход

сформулирован

для

распределитель

-

ных

сетей

с

одним

источником

питания

и

, 

в

общем

случае

, 

не

дает

возможности

получить

расчетные

оценки

K

U

(

n

)

в

узлах

питающих

электрических

сетей

напряжением

 110 

кВ

и

выше

, 

а

также

определить

пе

-

речни

резонансных

частот

для

данных

узлов

.

АЛГОРИТМ

РАЗРАБОТАННОЙ

МЕТОДИКИ

ФОРМИРОВАНИЯ

МАТЕМАТИЧЕСКОЙ

МОДЕЛИ

ЭЭС

Основной

проблемой

при

решении

рассматривае

-

мой

задачи

является

зависимость

частотных

свойств

электрической

цепи

от

количества

и

параметров

ре

-

активных

элементов

 [11], 

ввиду

чего

именно

резуль

-

таты

расчетов

ЧХ

, 

в

первую

очередь

, 

будут

опреде

-

ляться

охватом

зоны

ЭЭС

, 

включенной

в

модель

.

При

проведении

расчетов

несинусоидальных

УР

и

исследовании

частотных

свойств

ЭЭС

дополнитель

-

но

требуется

учитывать

следующие

особенности

:

1. 

В

синхронизированных

ЭЭС

предельно

допусти

-

мое

отклонение

частоты

составляет

 ±0,4 

Гц

 [3]. 

Следовательно

, 

на

частоте

n

-

й

гармоники

модуль

и

фаза

входного

сопротивления

ЭЭС

относи

-

тельно

узла

может

принимать

любое

значение

, 

соответствующее

АЧХ

и

ФЧХ

в

полосе

частот

(50,00 ± 0,4) 

∙

n

Гц

.

2. 

Для

кривых

АЧХ

характерны

острые

максимумы

и

минимумы

, 

что

обусловлено

доминирующим

ха

-

рактером

реактивных

сопротивлений

по

сравне

-

нию

с

активными

1

. 

При

этом

включение

в

модель

Рис

. 1. 

ЧХ

эквивалентного

сопротивления

ЭЭС

относительно

шин

 110 

кВ

питающего

центра

при

применении

упро

-

щенного

подхода

и

подробной

математической

модели

: 

а

) 

АЧХ

; 

б

) 

ФЧХ

1

В

особенности

для

электрических

сетей

напряжением

 110 

кВ

и

выше

.

57

дополнительных

элементов

может

сопровождать

-

ся

качественными

изменениями

ЧХ

 — 

возникно

-

вением

новых

резонансных

частот

, 

а

также

сме

-

щением

существующих

. 

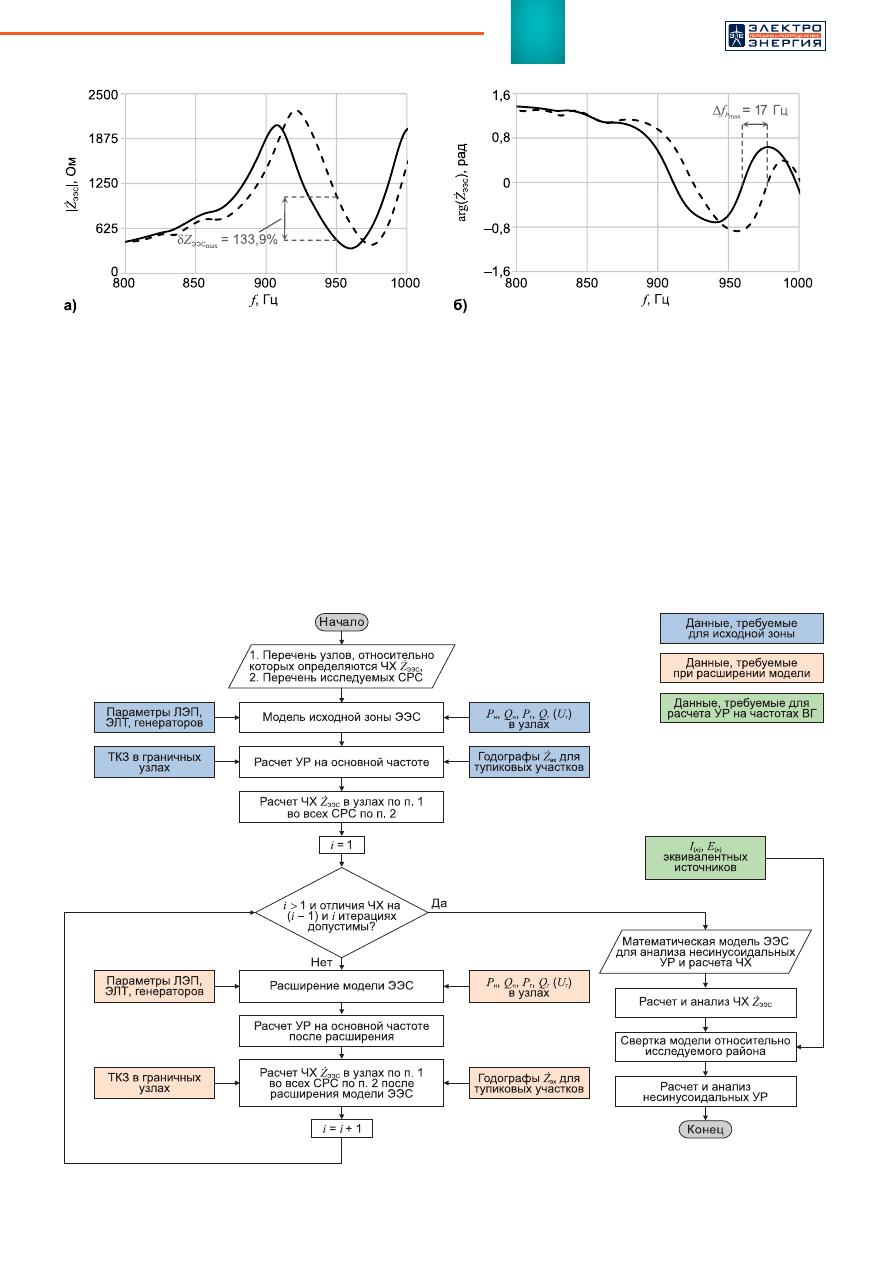
Поэтому

отличия

модуля

и

фазы

входного

сопротивления

ЭЭС

на

одной

и

той

же

частоте

относительно

одного

и

того

же

узла

при

изменении

состава

элементов

, 

включен

-

ных

в

математическую

модель

, 

могут

достигать

десятков

и

сотен

процентов

 (

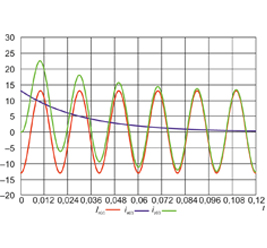
рисунок

 2).

С

учетом

указанных

фактов

, 

математическую

мо

-

дель

ЭЭС

для

расчетов

несинусоидальных

УР

и

ЧХ

предлагается

формировать

в

соответствии

с

алгорит

-

мом

, 

блок

-

схема

которого

представлена

на

рисунке

 3.

Предлагаемый

подход

основан

на

рекоменда

-

циях

 [6], 

согласно

которым

расширение

математиче

-

ской

модели

ЭЭС

следует

проводить

итерационно

, 

путем

последовательного

ее

развертывания

отно

-

сительно

исходной

зоны

. 

В

ее

составе

должны

быть

представлены

:

– 

узлы

, 

относительно

которых

проводятся

расче

-

ты

ЧХ

входных

сопротивлений

  (

анализируемые

узлы

), 

и

элементы

ЭЭС

, 

влияние

режимов

работы

Рис

. 2. 

Влияние

размеров

зоны

, 

включаемой

в

математическую

модель

ЭЭС

, 

на

вид

ЧХ

входных

сопротивлений

относительно

узла

 110 

кВ

в

полосе

частот

 800–1000 

Гц

: 

а

) 

АЧХ

; 

б

) 

ФЧХ

 (

сплошными

линиями

показаны

исходные

графики

ЧХ

, 

пунктиром

 — 

при

расширении

зоны

моделирования

)

Рис

. 3. 

Блок

-

схема

алгоритма

формирования

математической

модели

ЭЭС

для

проведения

расчетов

несинусои

-

дальных

УР

и

ЧХ

 (

ТКЗ

 — 

ток

короткого

замыкания

, 

СРС

 — 

схемно

-

режимная

ситуация

)

№

 4 (79) 2023

58

КАЧЕСТВО 

ЭЛЕКТРОЭНЕРГИИ

и

коммутационного

состояния

которых

на

харак

-

тер

ЧХ

является

предметом

исследования

 (

влия

-

ющие

элементы

);

– 

все

элементы

ЭЭС

в

зонах

, 

ограниченных

пя

-

тым

поясом

1

относительно

анализируемых

узлов

, 

а

также

точек

присоединения

влияющих

элемен

-

тов

 [7, 9]; 

если

граничные

узлы

зон

расположены

на

связях

 110 

кВ

и

выше

, 

нормально

замкнутых

или

замыкаемых

в

рассматриваемых

схемно

-

режимных

ситуациях

 (

СРС

), 

то

границы

зон

долж

-

ны

быть

расширены

до

шин

ближайших

узловых

ПС

или

электростанций

 (

в

том

числе

связывающих

сети

разных

классов

напряжения

, 

если

граничные

узлы

лежат

на

взаимно

шунтирующих

транзитах

);

– 

элементы

ЭЭС

, 

образующие

кратчайшие

связи

между

анализируемыми

узлами

и

узлами

присо

-

единения

влияющих

элементов

, 

замкнутые

в

нор

-

мальной

схеме

или

замыкаемые

в

рассматри

-

ваемых

СРС

и

отделенные

не

более

чем

двумя

трансформациями

напряжения

 [7];

– 

при

проведении

расчетов

ЧХ

относительно

узлов

6–35 

кВ

 — 

соответствующие

фрагменты

распре

-

делительных

сетей

 (

от

шин

питающих

центров

до

наиболее

удаленных

точек

).

Для

исходной

зоны

ЭЭС

проводится

расчет

УР

на

основной

частоте

, 

в

ходе

которого

определяют

-

ся

потребляемая

активная

и

реактивная

мощности

в

узлах

, 

а

также

напряжение

в

них

. 

Достоверность

полученных

результатов

оценивается

по

величине

отклонений

расчетных

значений

режимных

параме

-

тров

от

измеренных

в

соответствии

с

критериями

, 

применяемыми

при

верификации

моделей

регио

-

нальных

ЭЭС

и

ОЭС

 (

таблица

 1).

На

основании

результатов

расчета

УР

на

основ

-

ной

частоте

доопределяются

параметры

математи

-

ческой

модели

в

нагрузочных

и

граничных

узлах

.

Для

узлов

 6–35 

кВ

с

присоединенной

комплекс

-

ной

нагрузкой

определяются

частотные

годографы

сопротивления

. 

При

исследовании

ЧХ

применитель

-

но

к

сетям

напряжением

 35 

кВ

и

ниже

аналогичные

расчеты

проводятся

для

нагрузочных

узлов

напря

-

жением

ниже

 1 

кВ

.

Для

фрагментов

ЭЭС

напряжением

 110 

кВ

и

выше

, 

представляемых

при

расчетах

УР

на

основной

часто

-

те

отборами

мощности

, 

а

на

частотах

ВГ

 — 

частот

-

ными

эквивалентами

2

, 

определяются

активное

и

ин

-

дуктивное

сопротивление

эквивалента

согласно

 [21]. 

К

числу

таких

фрагментов

относятся

:

– 

тупиковые

участки

сети

 110 

кВ

, 

для

которых

токо

-

вые

нагрузки

ЛЭП

и

уровни

напряжения

на

шинах

ПС

в

нормальных

и

послеаварийных

режимах

на

-

ходятся

в

допустимых

пределах

;

– 

проходные

и

отпаечные

ПС

 110–220 

кВ

, 

к

шинам

которых

не

подключены

СКРМ

и

на

шины

которых

не

осуществляется

выдача

мощности

электро

-

станций

.

Зона

ЭЭС

, 

внешняя

по

отношению

к

исходной

, 

представляется

путем

задания

в

граничных

узлах

сопротивлений

, 

определяемых

суммой

токов

, 

под

-

питывающих

каждый

граничный

узел

по

внешним

связям

при

трехфазном

КЗ

. 

Для

расчета

сопротив

-

лений

определяются

периодические

составляющие

токов

трехфазного

КЗ

в

начальный

момент

време

-

ни

, 

при

этом

УР

на

основной

частоте

, 

рассчитанный

на

предыдущем

этапе

, 

рассматривается

в

качестве

предшествующего

режима

. 

Если

возможность

рас

-

чета

токов

КЗ

отсутствует

, 

то

целесообразно

ори

-

ентироваться

на

отчетные

данные

о

минимальных

и

максимальных

уровнях

токов

трехфазных

КЗ

, 

однако

все

дальнейшие

расчеты

ЧХ

в

этом

случае

проводятся

для

двух

соответствующих

значений

сопротивлений

КЗ

. 

После

доопределения

параметров

модели

ЭЭС

в

границах

исходной

зоны

производятся

расчеты

АЧХ

и

ФЧХ

входных

сопротивлений

относительно

анали

-

зируемых

узлов

во

всех

рассматриваемых

СРС

.

Далее

перечисленные

выше

действия

повторя

-

ются

при

последовательном

итерационном

расши

-

рении

зоны

ЭЭС

, 

включаемой

в

математическую

модель

. 

С

целью

сокращения

количества

итераций

расширение

следует

производить

одновременно

относительно

всех

граничных

узлов

до

ближайших

узловых

ПС

, 

соединяющих

взаимно

шунтирующие

участки

электрической

сети

напряжением

 110 

кВ

и

выше

.

Критерием

окончания

итерационного

процесса

является

выполнение

комплекса

условий

для

АЧХ

и

ФЧХ

входных

сопротивлений

относительно

каждо

-

1

Границы

таких

зон

задают

узлы

, 

связанные

с

указанными

узлами

не

более

чем

пятью

последовательно

включенными

элементами

. 

При

этом

нормально

замкнутые

секции

шин

рассматриваются

как

один

узел

.

2

Под

частотным

эквивалентом

в

общем

виде

понимается

R

-

X

шунт

с

частотно

-

зависимыми

параметрами

, 

сопротивление

ко

-

торого

равно

входному

сопротивлению

соответствующего

участка

сети

на

каждой

частоте

рассматриваемого

диапазона

 [21].

Табл

. 1. 

Практические

критерии

достоверности

результатов

расчетов

УР

на

основной

частоте

Параметр

Допустимое

отклонение

Генерация

активной

мощности

Не

допускается

Генерация

реактивной

мощности

2% 

или

 10 

Мвар

Перетоки

активной

 (

реактивной

) 

мощности

по

сетевым

элементам

5% 

или

 10 

МВт

 (20 

Мвар

)

Сальдо

перетоков

активной

 (

реактивной

) 

мощности

5% 

или

 10 

МВт

 (20 

Мвар

)

Уровни

напряжения

в

узлах

:

– 

до

 500 

кВ

1% 

или

 2 

кВ

– 500 

кВ

и

выше

3 

кВ

Примечание

: 

допустимые

отклонения

определяются

как

 max (



%, 



и

.

е

.), 

где



% — 

отклонение

в

процентах

, 

переведенное

в

имено

-

ванные

единицы

, 

а



и

.

е

. — 

отклонение

в

именованных

единицах

.

59

го

анализируемого

узла

во

всех

рассматриваемых

СРС

, 

определенных

на

 (

i

 – 1)-

й

и

i

-

й

итерациях

, 

в

по

-

лосах

частот

, 

соответствующих

гармоникам

вплоть

до

 40 

порядка

:

– 

относительная

разность

наименьшего

, 

наиболь

-

шего

и

экстремальных

значений

модуля

входного

сопротивления

в

полосе

частот

, 

соответствующей

n

-

й

гармонике

 (



Z

min

, 



Z

max

, 



Z

extr

), 

не

превышает

 5%;

– 

относительная

разность

значений

фазового

угла

, 

соответствующих

наименьшим

, 

наибольшим

и

экс

-

тремальным

значениям

модуля

входного

сопротив

-

ления

 (



φ

Ż

min

, 



φ

Ż

max

, 



φ

Ż

extr

), 

не

превышает

 5%;

– 

в

полосе

частот

каждой

ВГ

количество

нулей

ФЧХ

остается

постоянным

.

Важно

отметить

, 

что

с

учетом

области

применения

схем

замещения

элементов

ЭЭС

, 

значений

предельно

допустимых

отклонений

основной

частоты

и

рекомен

-

даций

 [6], 

расчеты

ЧХ

проводятся

с

шагом

 1 

Гц

для

гар

-

моник

порядков

с

 4 

по

 40, 

что

соответствует

диапазону

частот

 198–2020 

Гц

. 

При

этом

для

выполнения

расче

-

тов

на

частотах

 2-

й

и

 3-

й

гармоник

упрощенные

схемы

замещения

комплексной

нагрузки

не

применимы

1

, 

что

ограничивает

расчетный

диапазон

частот

.

Вышеприведенные

условия

позволяют

опреде

-

лить

границу

района

ЭЭС

, 

задание

которого

в

мате

-

матической

модели

позволяет

с

указанной

степенью

точности

отразить

частотные

свойства

энергосисте

-

мы

в

целом

и

, 

таким

образом

, 

сформировать

мате

-

матическую

модель

ЭЭС

для

расчетов

ЧХ

. 

Данная

модель

является

основой

для

проведения

анализа

качественных

изменений

АЧХ

и

ФЧХ

входных

сопро

-

тивлений

относительно

узлов

ЭЭС

в

исходно

опре

-

деленных

СРС

под

действием

влияющих

факторов

.

Поскольку

в

подавляющем

большинстве

случаев

количество

точек

, 

в

которых

производятся

измерения

режимных

параметров

основной

частоты

, 

значительно

превосходит

число

точек

контроля

КЭ

, 

для

расчетов

не

-

синусоидальных

УР

ЭЭС

необходимо

свернуть

полу

-

ченную

модель

относительно

элементов

, 

для

которых

известны

значения

K

U

(

n

)

и

K

I

(

n

)

на

интересующих

часто

-

тах

. 

Важно

, 

что

для

получения

корректных

расчетных

значений

K

U

(

n

)

и

K

I

(

n

)

в

узлах

присоединения

нелинейных

элементов

требуется

задавать

значения

комплексов

ВГ

тока

, 

а

в

граничных

узлах

 — 

комплексов

ВГ

напряже

-

ния

, 

что

позволяет

учесть

возможное

взаимное

подав

-

ление

  (

полное

или

частичное

) 

гармоник

токов

в

вет

-

вях

 [8]. 

В

условиях

дефицита

измерений

ПКЭ

зачастую

применяется

принцип

наихудших

расчетных

условий

, 

согласно

которому

токи

и

ЭДС

источников

на

частоте

каждой

ВГ

полагаются

синфазными

, 

что

упрощает

ре

-

шение

задачи

, 

но

приводит

к

увеличению

капиталоем

-

кости

технических

мероприятий

 [6, 7, 10, 14].

По

результатам

расчетов

несинусоидальных

УР

, 

выполняемых

с

использованием

преобразованной

модели

, 

могут

быть

получены

оценки

K

U

(

n

)

и

K

I

(

n

)

для

интересующих

узлов

и

элементов

ЭЭС

в

рассматри

-

ваемых

СРС

, 

что

 (

вкупе

с

результатами

расчетов

ЧХ

) 

позволяет

разработать

технические

решения

по

нор

-

мализации

соответствующих

ПКЭ

.

ОСОБЕННОСТИ

МОДЕЛИРОВАНИЯ

ОТДЕЛЬНЫХ

ЭЛЕМЕНТОВ

ЭЭС

Исходное

требование

к

универсальности

матема

-

тической

модели

обуславливает

необходимость

учитывать

ряд

особенностей

, 

связанных

с

пред

-

ставлением

ее

элементов

на

частотах

ВГ

и

напря

-

мую

влияющих

на

процесс

формирования

моде

-

ли

, 

уже

при

проведении

расчетов

УР

на

основной

частоте

. 

Несмотря

на

то

, 

что

вопросы

моделирова

-

ния

элементов

ЭЭС

на

частотах

ВГ

подробно

рас

-

смотрены

в

литературе

 [6–8, 10, 22, 23], 

следует

отметить

ряд

дополнительных

практических

аспек

-

тов

, 

подлежащих

учету

.

Моделирование

ЛЭП

. 

Для

неоднородных

ЛЭП

следует

задавать

все

входящие

в

их

состав

участки

в

соответствии

с

порядком

их

следования

по

трас

-

се

, 

причем

каждый

из

них

должен

быть

представлен

отдельной

неидеализированной

линией

с

распре

-

деленными

параметрами

. 

Если

применяемый

для

расчетов

ПВК

позволяет

задавать

частотные

зави

-

симости

поперечных

проводимостей

и

продольных

сопротивлений

несимметричных

П

-

образных

схем

замещения

, 

то

ЛЭП

может

быть

представлена

в

мо

-

дели

ЭЭС

единственной

ветвью

с

сосредоточенными

параметрами

, 

которые

предварительно

определяют

-

ся

методом

эквивалентного

четырехполюсника

 [11], 

после

чего

осуществляется

их

привязка

к

модели

.

Для

всех

ЛЭП

напряжением

 6–35 

кВ

, 

отражаемых

в

модели

ЭЭС

, 

требуется

учитывать

емкостные

про

-

водимости

. 

Кабельные

вводы

в

КРУЭ

 35 

кВ

и

выше

необходимо

задавать

отдельными

ветвями

.

Моделирование

СКРМ

и

ФКУ

. 

Плавно

регулиру

-

емые

СКРМ

целесообразно

представлять

в

виде

комбинации

опорного

по

напряжению

узла

, 

соответ

-

ствующего

нелинейному

регулируемому

элементу

, 

а

также

элементов

, 

моделирующих

присоединенные

на

стороне

переменного

тока

БСК

, 

ШР

и

ФКУ

. 

На

ча

-

стотах

ВГ

нелинейный

элемент

может

представлять

-

ся

идеальным

или

неидеальным

источником

тока

; 

в

последнем

случае

требуется

задать

частотный

го

-

дограф

входного

сопротивления

элемента

со

сторо

-

ны

переменного

тока

2

. 

Нерегулируемые

ШР

и

БСК

задаются

реактивны

-

ми

шунтами

, 

при

этом

для

БСК

следует

учитывать

включенные

последовательно

токоограничивающие

реакторы

. 

Многозвенные

пассивные

ФКУ

целесообразно

задавать

в

модели

набором

шунтов

для

удобства

учета

коммутационного

состояния

звеньев

. 

Пассив

-

ные

ФКУ

более

сложных

конфигураций

с

целью

сни

-

жения

размерности

модели

ЭЭС

следует

задавать

либо

в

явном

виде

согласно

их

схеме

, 

либо

частот

-

ным

годографом

входного

сопротивления

.

Моделирование

комплексной

нагрузки

. 

По

-

скольку

на

практике

сведения

о

составе

включен

-

ных

электроприемников

потребителей

чаще

всего

отсутствуют

, 

при

расчетах

УР

на

частотах

ВГ

ис

-

пользуются

схемы

замещения

комплексной

нагруз

-

ки

 0,4–35 

кВ

. 

Схемы

замещения

, 

рекомендуемые

1

Пояснение

причин

приведено

в

описании

применяемой

схемы

замещения

комплексной

нагрузки

.

2

Подобная

зависимость

, 

в

частности

, 

является

паспортной

характеристикой

СТАТКОМов

 [6].

№

 4 (79) 2023

60

КАЧЕСТВО 

ЭЛЕКТРОЭНЕРГИИ

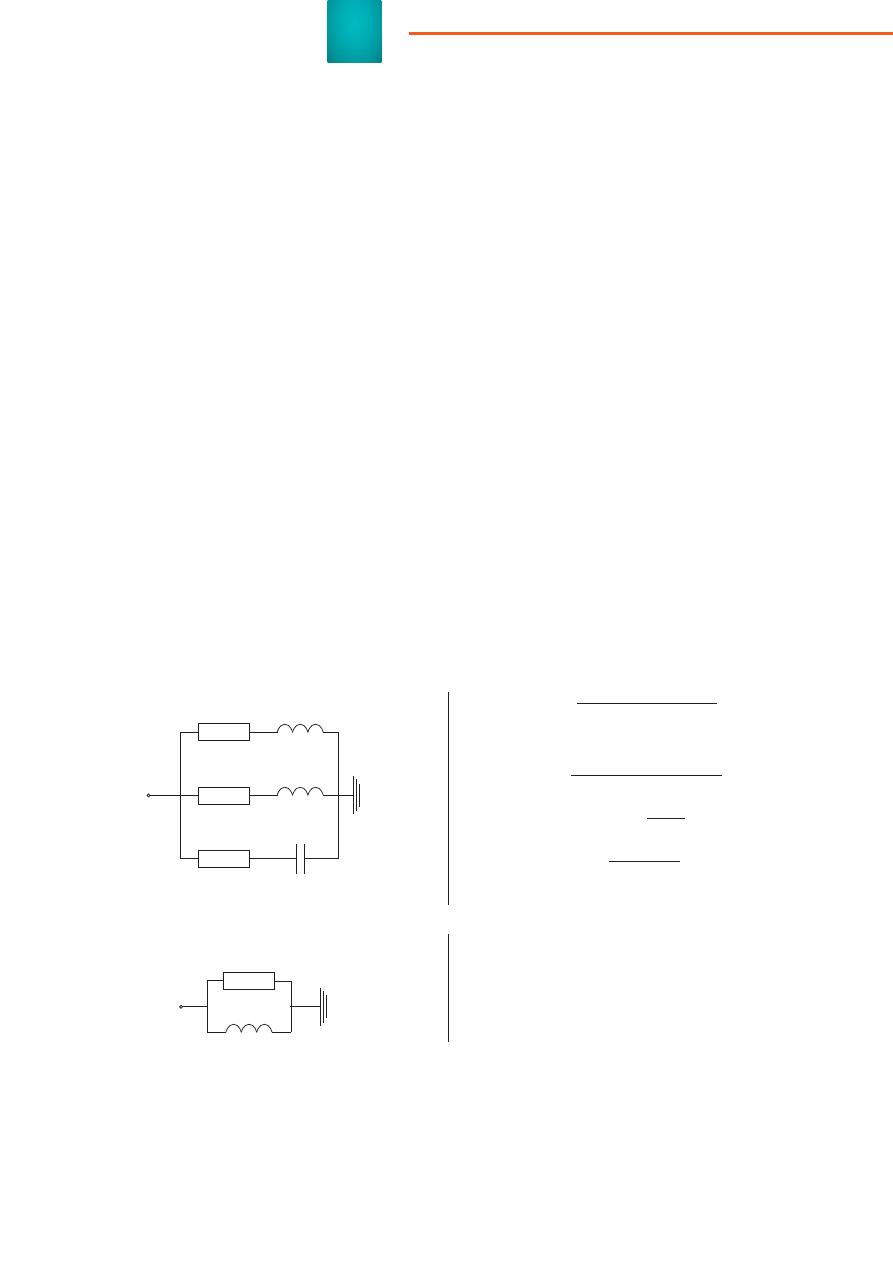
к

применению

в

 [6, 8, 22], 

приведены

на

рисунке

 4. 

При

расчете

их

параметров

по

формулам

 (3)–(10) 

значения

потребляемой

активной

мощности

в

узле

должны

быть

приведены

к

номинальному

напря

-

жению

с

учетом

СХН

. 

При

отсутствии

сведений

о

составе

нагрузки

с

дифференциацией

по

типам

электроприемников

  (

линейная

статическая

, 

двига

-

тельная

, 

нелинейная

) 

целесообразно

ориентиро

-

ваться

на

данные

 [23]. 

Разделение

двигательной

нагрузки

на

синхрон

-

ную

и

асинхронную

обычно

не

требуется

, 

поскольку

значения

сопротивлений

обратной

последователь

-

ности

синхронных

двигателей

и

сопротивлений

КЗ

асинхронных

двигателей

  (

АД

) 

в

о

.

е

., 

а

также

соот

-

ношений

их

активных

и

индуктивных

составляю

-

щих

оказываются

численно

близкими

. 

Нелинейная

составляющая

нагрузки

  (

на

рисунке

 4 

не

показана

) 

представляется

эквивалентным

источником

тока

, 

па

-

раметры

которого

определяются

отдельно

с

учетом

рекомендаций

 [6, 8, 14, 22].

Следует

отметить

, 

что

представление

АД

со

-

противлением

КЗ

является

допустимым

только

на

частотах

ВГ

свыше

 3 

порядка