

«КАБЕЛЬ-news», декабрь-январь 2009/2010
90
Технологии расчетов
ÄÈÝËÜÊÎÌÅÒÐÈß
Для исследования слабопогло-
щающих диэлектриков, применяемых
в качестве электрической изоляции
кабельных изделий, удобным являет-
ся метод цилиндрического объемного
резонатора с колебанием
H
01p
. Данный
метод широко используется для изме-
рения относительной диэлектричес-
кой проницаемости
ε
и тангенса угла
диэлектрических потерь tg
δ
полиме-
ров (ПЭ, ПТФЭ и их производных) на
СВЧ [1—4]. Метод рекомендован стан-
дартом IEC (Международная электро-
техническая комиссия — МЭК) [5] и его
отечественными аналогами [5, 6]. Сле-
дует отметить, что расчетные формулы
для tg
δ
в рекомендациях [6, 7] разли-
чаются между собой и дают разные ре-
зультаты. В России с 01.06.2008 введен
ГОСТ Р 8.623-2006 [8], в котором метод
изложен с уточнениями [9].
В ФГУП «ОКБ КП» используется
измерительная установка с цилин-
дрическим резонатором ОР-4 на ко-
лебании
H
014
(разработчик — Восточно-
Сибирский НИИ физико-технических
и радиотехнических измерений, г.
Иркутск) (рис. 1, 2). Установка предна-
значена для исследования характери-
стик твердых диэлектриков в форме
дисков на частотах диапазона от 9 до
10 ГГц. Диапазон измеряемых на уста-
новке значений
ε
варьируется от 1,2
до 10, диапазон измерения tg
δ
— от
3·10
-5
до 5·10
-2
. Используемый метод
соответствует ГОСТ Р 8.623 — 2006 и
заключается в измерении параметров
цилиндрического
H
01p
-резонатора
без диэлектрического образца и с об-
разцом в виде диска на подвижном
бесконтактном поршне при неизмен-
ной резонансной частоте (рис. 3). Ис-
ходными параметрами для расчета
ε
1
и tg
δ
образца являются: длина пустого
резонатора
L
0
, его резонансная часто-
та
f
0
и добротность
Q
0
, диаметр резона-
тора
D
= 2
a
, перемещение подвижного
поршня Δ
L
, необходимое для восста-
новления резонансной частоты
f
ε
по-
сле помещения образца в резонатор (
f
ε
= f
0
), толщина образца
t
и добротность
резонатора с образцом
Q
ε
.
В стандарте [7] вместо добротности
Q
0
,
Q
ε
измеряется ослабление, вно-
симое в тракт пустым резонатором и
резонатором с образцом. Различие
расчетных формул для tg
δ
в докумен-
тах [5—7] связано с различными вари-
антами метода и приближениями. Од-
ним из приближений является замена
собственной добротности пустого ре-
зонатора
Q
00
и резонатора с образцом
Q
0ε
на нагруженную добротность
Q
0
,
Q
ε
.
Используемые обычно приближения и
упрощения могут приводить к значи-
тельным погрешностям, в частности,
к «отрицательным» значениям tg
δ
при
измерении слабопоглощающих мате-
риалов. Причина этого рассмотрена
в [9], где предложен вариант метода
измерения, свободный от упомянутых
допущений и устраняющий появление
«отрицательных» tg
δ
. Диэлектричес-
кая проницаемость образца рассчиты-
вается как [9]
(1)
где
x
=
h
1
t
находится из уравнения
(2)
и учтены равенства
L
ε
= L
0
– Δ
L
;
h
2
L
0
=
pπ
;
p
= 1, 2, 3, 4... — число полуволн
в пустом резонаторе;
q
= 0, 1, 2… —
число полуволн (максимумов элек-
трического поля) на толщине образца;
h
i
— продольное волновое число в
заполненной образцом (
i
= 1) и пустой
(
i
= 2) частях резонатора,
h
i
2
=
k
i
2
–
χ
2
,
ω
= 2
πf
ε
— круговая
резонансная частота,
χ = ν
11
/
a
— по-
перечное волновое число резонатора,
ν
11
= 3,831706 — корень функции Бес-
Метод объемного
цилиндрического резонатора
H
01p
для исследования
диэлектриков на СВЧ
В.Н. Егоров, В.В. Костромин, Б.С. Романов
«КАБЕЛЬ-news», декабрь-январь 2009/2010
91
Технологии расчетов
ÄÈÝËÜÊÎÌÅÒÐÈß
селя
J
1
(
z
),
ε
1
— диэлектрическая прони-
цаемость измеряемого образца (
i
= 1)
и воздуха в «пустой» части резонато-
ра (
i
= 2) относительно вакуума (при
нормальных условиях
ε
2
= 1,00058),
c
= 299,792458·10
9
мм·с
-1
— скорость
света в вакууме.
Метод определения тангенса угла
диэлектрических потерь tg
δ
основан
на измерении собственной доброт-
ности резонатора с исследуемым об-
разцом диэлектрика и сравнении ее
с собственной добротностью резона-
тора без образца с учетом изменения
распределения поля и омических по-
терь в стенках резонатора после вве-
дения исследуемого образца. Отличие
«омической» добротности резонатора
с образцом
Q
R
от собственной до-
бротности резонатора без образца
(имеющего только омические поте-
ри)
Q
00
удобно выразить параметром
η = Q
00
/
Q
R
. Тогда выражение для tg
δ
примет наиболее общий вид [9]
(3)
Для расчета tg
δ
по (3) необходимы
значения собственной добротности
пустого резонатора
Q
00
и резонатора
с образцом
Q
0ε
, которые определяются
экспериментально, и величины
K
1
E
,
η
.
Для расчета параметров
K
1
E
,
η
необхо-
димо, в частности, вычислить полный
запас энергии и мощность омических
потерь в резонаторе с образцом (а не
только в пустом резонаторе, как это
часто делается для упрощения). Коэф-
фициент заполнения резонатора
K
1
E
выразится как [9]
(4)
где
Параметры Ф
1
, Ф
2
учитывают пере-
распределение энергии между об-
разцом и пустой частью резонатора
при отклонении толщины образца
от полуволновой (кратной ей), когда
Ф
1
= Ф
2
= 1. Отметим, что
K
1
E
является
осциллирующей функцией электри-
ческой толщины образца
x
с миниму-
мами при полуволновой и кратной
ей толщине образца (за исключением
полностью заполненного резонатора).
Размах осцилляций возрастает с ро-
стом
ε
1
измеряемого образца.
Выражение для
η
имеет вид [9]
(5)
где
геометрический фактор пустого
H
0тр
резо-
натора,
G
= Δ
0
Q
00
, Δ
0
— глубина скин-слоя в
стенках резонатора.
Наиболее существенными источ-
никами погрешности измерения дан-
ным методом являются погрешность
измерения толщины образца, пере-
мещения поршня резонатора, необхо-
димого для восстановления резонанс-
ной частоты после введения образца в
резонатор, и погрешность измерения
собственной добротности резонато-
ра. Измерение перемещений поршня
с неопределенностью 1 мкм произво-
дится преобразователем линейных пе-
ремещений ЛИР-17 с устройством циф-
ровой индикации ЛИР 511. Измерение
собственной добротности резонатора
осуществляется с помощью поляриза-
ционного аттенюатора Д3-33А, что по-
зволяет исключить неквадратичность
характеристики СВЧ детектора и изме-
рять коэффициенты связи резонатора
с трактом. Используемый резонатор
ОР-4 с внутренним диаметром 50 мм
обладает на частоте 9,365 ГГц доброт-
ностью 30 000 на колебании
H
014
.
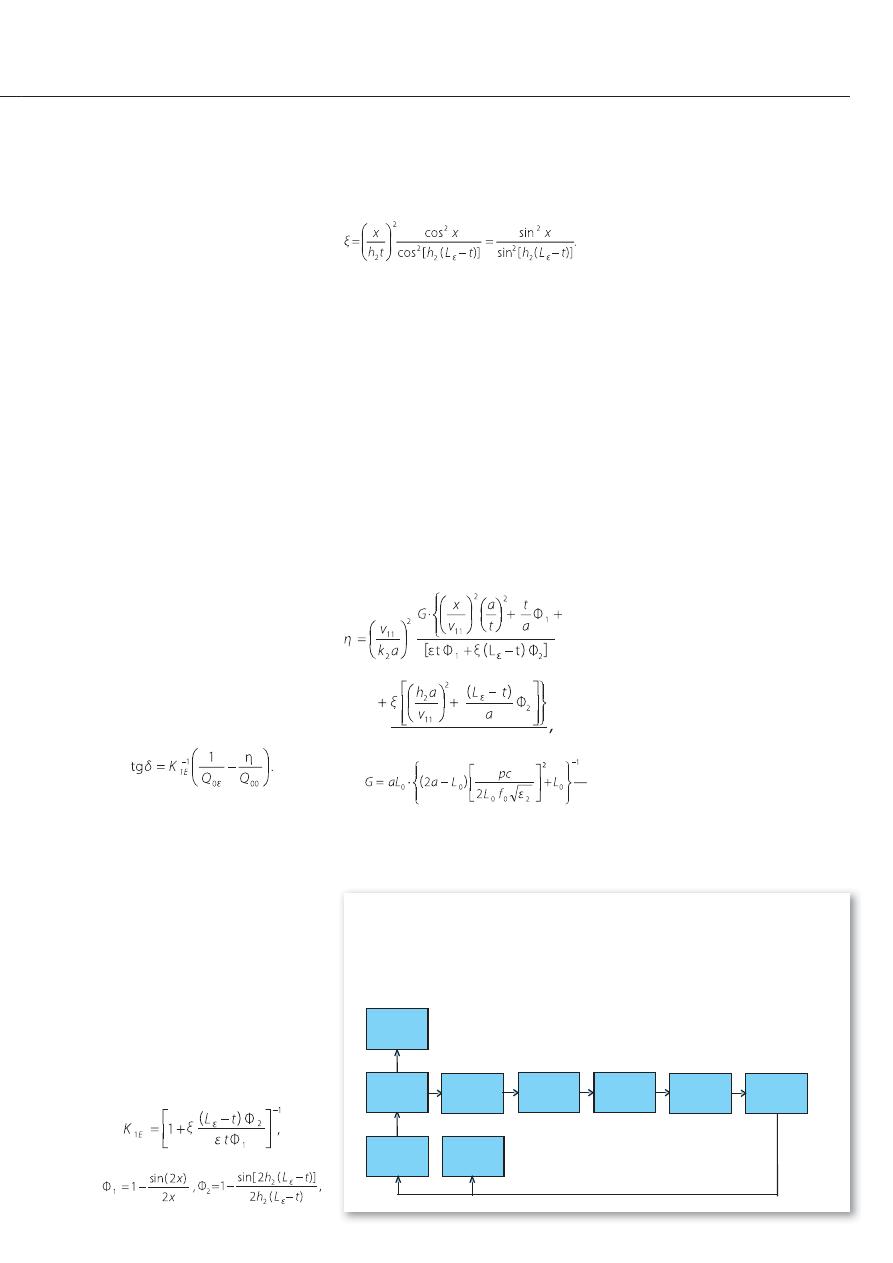
Структурная схема установки при-
ведена на рис. 1. Сигнал СВЧ генерато-
ра
1
подается на частотомер
2
и через
развязывающий ферритовый вентиль
4
и поляризационный аттенюатор
5
—
на измерительный резонатор
6
. С вы-
хода резонатора сигнал поступает на
1
3
2
4
5
6
7
9
8
Рис. 1. Структурная схема измерительной установки:
1
— генератор СВЧ;
2
— частотомер;
3
— индикатор резонанса (осциллограф)
с выходом напряжения развертки;
4, 7
— развязывающий вентиль;
5
— аттенюатор поляризационный волноводный;
6
— измерительный резонатор;
8
— детектор СВЧ;
9
— вольтметр

«КАБЕЛЬ-news», декабрь-январь 2009/2010
92
Технологии расчетов
ÄÈÝËÜÊÎÌÅÒÐÈß
развязывающий вентиль
7
и далее на
СВЧ детектор
8
, выходное напряжение
которого наблюдается на индикаторе
резонанса
3
и измеряется вольтметром
9
. Генератор СВЧ 1 работает в двух ре-
жимах: непрерывной генерации (НГ) и
линейной частотной модуляции (ЛЧМ)
сигналом пилообразного напряжения
горизонтальной развертки индикатора
резонанса
3
. Измерение резонансной
частоты, нагруженной добротности и
вносимого резонатором ослабления
проводится в режиме НГ.
Внешний вид действующей уста-
новки приведен на рис. 2.
В измерительной установке приме-
нены следующие серийные приборы и
оборудование:
1. Генератор СВЧ Г4-83 (Г4-111);
2. Аттенюатор поляризационный
волноводный Д3-33А;
3. Частотомер Ч3-69, (Ч3-61, Ч3-54 с
блоком Я3Ч-88 или Я3Ч-43);
4. Вентиль ферритовый 3ВВС-100;
5. Датчик перемещения ЛИР-17 с
устройством индикации ЛИР-511;
6. Микрометр МК-25;
7. Вольтметр В7-40 (В7-32);
9. Осциллограф С1-76.
10. Измерительный резонатор с ко-
лебанием Н
014
(его схематическое изо-
бражение приведено на рис. 3).
В последнем варианте установки
вместо генератора, частотомера, поля-
ризационного аттенюатора, детектора
СВЧ, вольтметра и осциллографа ис-
пользуется измеритель модуля коэффи-
циента передачи и отражения Р2М-18.
Измерительный резонатор должен
иметь собственную добротность не ме-
нее 30 000, переходное ослабление на
резонансной частоте не менее 30 дБ и
механизм перемещения подвижного
поршня не менее 25 мм с погрешно-
стью отсчета положения поршня не
более 0,005 мм. Измеряемый обра-
зец должен входить в резонатор без
усилий и свободно выходить из него
под собственным весом, оставаясь на
поршне при его отводе вниз.
Геометрические размеры образца
и допуски:
• диаметр образца — 49,9
-0,1
мм;
• отклонение от плоскопараллель-
ности торцевых поверхностей образ-
ца — не более 0,02 мм;
• неперпендикулярность боковой
поверхности образца к торцу — не бо-
лее 0,02 мм.
Толщину образца
t
вычисляют по
формуле:
где
λ = с
/
f
0
— длина волны в свободном
пространстве на частоте измерения, мм;
ε
1
— диэлектрическая проницаемость
материала образца, взятая из априор-
ных данных или из анализа измерений
образцов разной толщины из одного
материала;
a
— радиус резонатора, мм;
m
— целое число, равное 1, 2, 3...
Предпочтительнее для измерений
использовать образцы полуволновой
толщины (
m
= 1). Толщину образца из-
меряют в десяти точках с погрешностью
не более ±0,01 мм и усредняют.
Диэлектрическую проницаемость
ε
1
исследуемого образца относитель-
но вакуума вычисляют по формуле
(1). При необходимости диэлектриче-
ская проницаемость образца относи-
тельно окружающей среды (воздуха)
может быть пересчитана как
ε = ε
1
/
ε
2
.
Тангенс угла диэлектрических потерь
tg
δ
исследуемого образца вычисляют
по формуле (3). Контроль точности
результатов измерений проводится
путем измерения диэлектрической
проницаемости и тангенса угла диэ-
лектрических потерь государственных
стандартных образцов ГСО 1683-79,
ГСО 1555-79, ГСО 50090-89 и стандарт-
ных образцов предприятия ДПФТД,
ДПКРД, ДПСТ38Д в соответствии с ин-
струкцией по их применению.
Точностные характеристики методи-
ки даются в терминах неопределенно-
сти измерений [10]. Анализ точности из-
мерения в
H
01p
-резонаторе проводился
в работе [11]. Расширенную неопреде-
ленность измерения диэлектрической
проницаемости
U
ε
определим по типу В
[10] через функцию
ε
1
=
ε
1
(
u
i
) от входных
величин
u
i
=
f
0
,
t
,
a
,
x
, ε
2
при коэффициен-
те охвата
k
= 2 и доверительной вероят-
ности
p
= 0,95. Коэффициенты влияния
находятся обычным образом с учетом
неявно заданных в (1), (2) функций
x = x
(Δ
L
,
t
,
h
2
),
h
2
=
h
2
(
f
0
,
a
,
ε
2
) и имеют вид
L
0
2
1
D
∆
L
t
L
ε
z
3
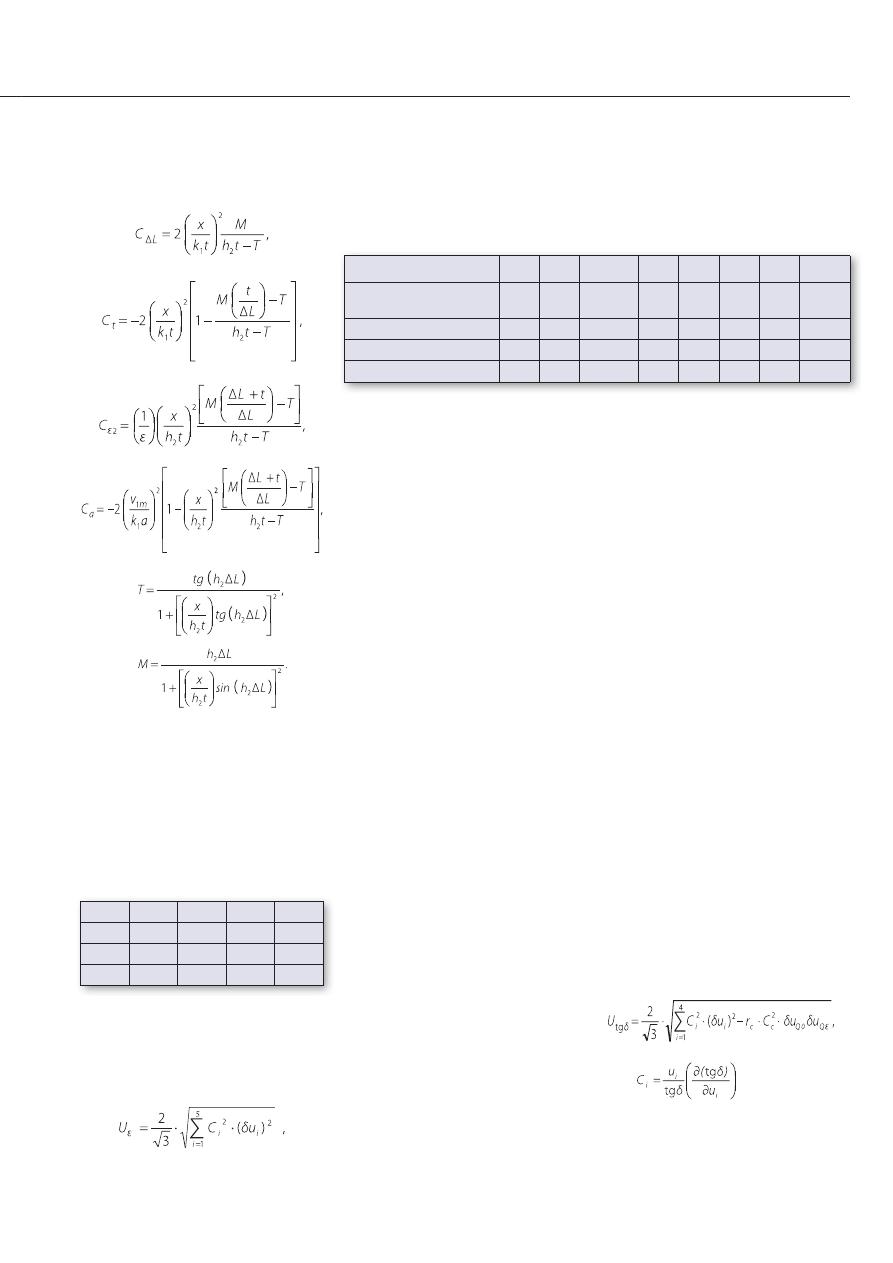
Рис.3. Схематическое изображение
резонатора:
1 — исследуемый образец;
2 — резонансная полость;
3 — подвижный поршень
Рис. 2. Внешний вид измери-
тельной установки
«КАБЕЛЬ-news», декабрь-январь 2009/2010
93
Технологии расчетов
ÄÈÝËÜÊÎÌÅÒÐÈß
(6)
где
В таблице 1 приведены типичные
значения границ относительной нео-
пределенности входных величин
δu
i
,
для расчета расширенной неопреде-
ленности по
ε
1
и tg
δ
.
Таблица 1. Значения относительных
неопределенностей входных величин
δ
Δ
L
δt
δa
δf
0
δQ
ε
5×10
-4
4×10
-4
4×10
-5
10
-7
2×10
-2
δQ
0
δη
δε
2
δL
δK
1
E
2×10
-2
10
-2
6×10
-5
2×10
-4
10
-2
В предположении равномерного
распределения составляющих
δu
i
рас-
ширенная неопределенность
ε
1
по
типу В выразится как
(7)
где
C
i
=
C
Δ
L
,
C
t
,
C
a
,
C
f
,
C
ε
2
и
δu
i
=
δ
(Δ
L
),
δt
,
δa
,
δf
0
,
δε
2
.
В таблице 2 представлены значения
коэффициентов влияния, результаты из-
мерений
ε
1
на частоте 9,365 ГГц в резо-
наторе диаметром 50,0 мм и расширен-
ная неопределенность
U
ε
для образцов
с толщиной, близкой к полуволновой.
Как видно из таблицы 2, при толщи-
не образцов, близкой к полуволновой
(
x ≈ π
), максимальное влияние оказы-
вают неопределенности величин Δ
L, a
,
ε
2
. Эта закономерность сохраняется и
для образцов с толщиной, кратной по-
луволне:
x = qπ, q
=1, 2, 3… При электри-
ческой толщине образца
x = π
(2
q
+ 1)/2,
q
= 0, 1, 2… (нечетное число четвер-
тей длины волны) наибольший вклад
в расширенную неопределенность
ε
1
дает неопределенность измерения
толщины образца
δt
. Неопределен-
ность настройки на резонанс (вос-
становления резонансной частоты)
δf
0
≈ (10
-2
÷10
-3
) ·
Q
ε
-1
~ 10
-6
÷10
-7
, несмотря
на большие значения коэффициента
C
f
,
не оказывает существенного влияния
на конечный результат при измерениях
образцов с
K
1
E
· tg
δ
<10
-4
.
В общем случае вид зависимости
U
ε
(
x,
ε
1
) определяется соотношением
вклада
δt
, имеющего минимумы при
x
=
qπ
и максимумы при
x = π
(2
q
+ 1)/2,
и вкладов
δ
(Δ
L
),
δa,
имеющих миниму-
мы при
x = π
(2
q
+ 1)/2 и максимумы при
x = qπ. Глубина осцилляций
U
ε
(
x
,
ε
1
) убы-
вает с ростом x и возрастает с ростом
ε
1
. При указанных в таблице 1 значениях
δ
(Δ
L
),
δa
,
δt
и
x
≈
π
, значение расширен-
ной неопределенности
ε
1
не является
минимально возможным. Зависимость
U
ε
(
x, ε
1
) (рис. 5) в этом случае имеет
максимумы в окрестностях
x = qπ
, и ми-
нимумы в окрестностях
x = π
(2
q
+ 1)/2,
что говорит об основном вкладе в
U
ε
величин
δ
(Δ
L
),
δa
, а не
δt
. Для преобла-
дающего вклада
δt
зависимость
U
ε
(
x, ε
1
)
имеет вид, представленный на рис. 6.
Рассмотрим неопределенность из-
мерения tg
δ
в соответствии с форму-
лой (3). В данном методе измерение
собственной добротности пустого ре-
зонатора
Q
00
и резонатора с образцом
Q
0ε
производится на одной частоте
при близких значениях мощности на
выходе резонатора. По этой причине
существующие систематические по-
грешности при измерении
Q
00
и
Q
0ε
оказываются в значительной степени
компенсированными, т.е. следует учи-
тывать корреляцию составляющих не-
определенности
δQ
00
и
δQ
0
ε
. Расширен-
ная относительная неопределенность
измерения tg
δ
(
K
1
E
,
Q
0
ε
,
Q
00
,
η
) в предпо-
ложении равномерного распределения
при доверительной вероятности 0,95 и
равномерной малости составляющих
выразится в соответствии с [11] как
(8)
где
— коэффициент
влияния
i
-той входной величины
u
i
=
K
1
E
,
Q
0
ε
,
Q
00
,
η
;
δu
i
= Δ
u
i
/
u
i
— стандартная отно-
сительная неопределенность
i
-той вход-
ной величины, задаваемая при расчете;
r
c
— коэффициент корреляции между
Таблица 2. Коэффициенты влияния и результаты измерения
ε
1
полуволновых образцов
с оценкой расширенной неопределенности
δ
ε
=
U
ε
Материал
x
C
Δ
L
C
t
C
a
C
f
C
ε
2
ε
1
δε
, %
Полиэтилен высокого
давления
3,136
-1,57
-3,5×10
-5
4,17
5,74
-3,87
2,282
0,1
Кварцевое стекло КВ
3,065
-3,10
-0,008
7,05
10,1
-6,07
3,807
0,2
Керамика ВК 94 -1
3,032
-6,78
-0,021
13,2
20,0
-11,0
9,19
0,3
Керамика ВК 100 -1
3,116
-7,11
-0,001
13,8
20,9
-11,4
9,66
0,3
«КАБЕЛЬ-news», декабрь-январь 2009/2010
94
Технологии расчетов
ÄÈÝËÜÊÎÌÅÒÐÈß
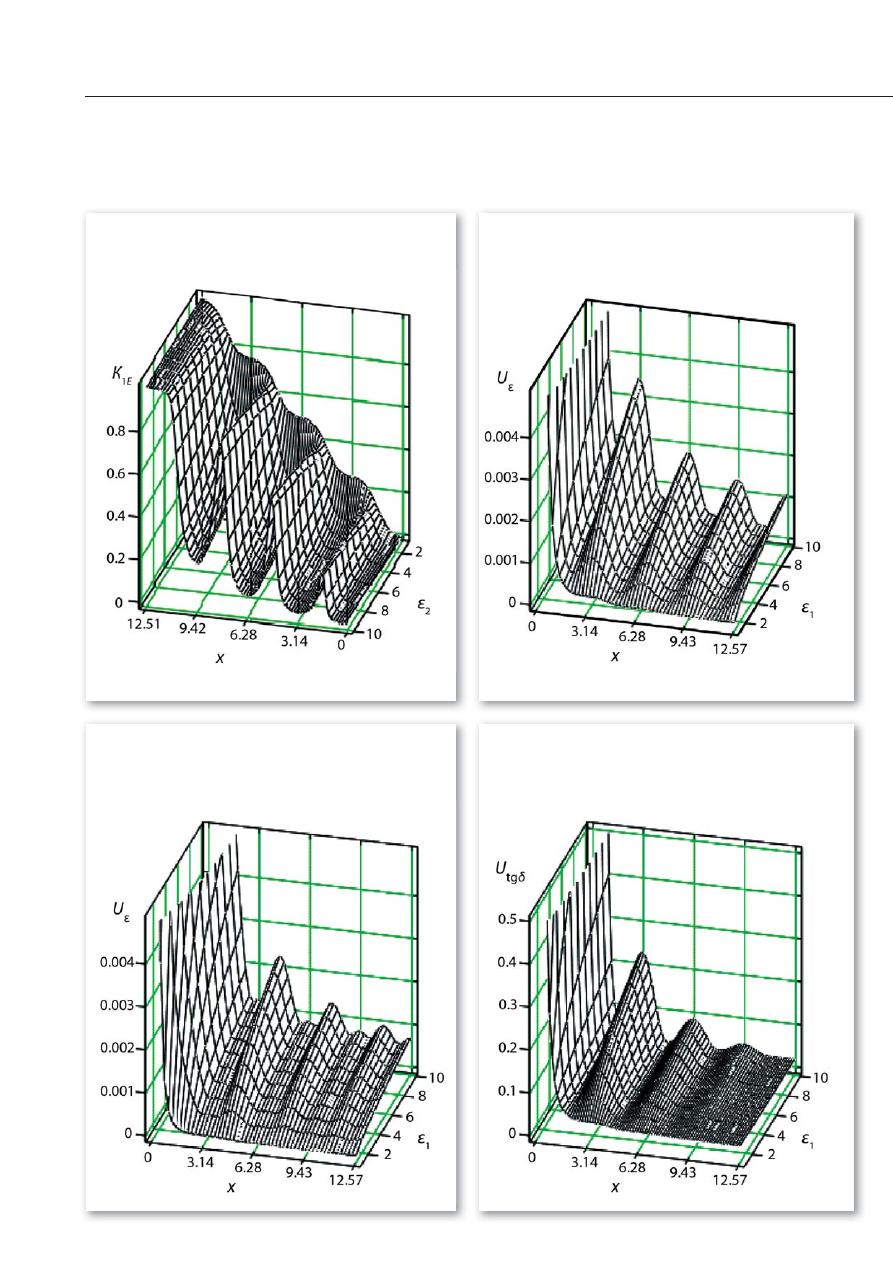
Рис. 4. Зависимость
K
1
E
(
x, ε
1)
в резонаторе H014
Рис. 5. Относительная неопределенность
U
ε
при Δ(Δ
L
) = 0,01 мм, Δ
t
= 0,003 мм
Рис. 6. Относительная неопределенность
U
ε
при
Δ(Δ
L
) = 0,003 мм, Δ
t
= 0,01 мм
Рис. 7. Относительная неопределенность Utgδ
при
δQ
00
= 0,02,
δQ
0
ε
= 0,02

«КАБЕЛЬ-news», декабрь-январь 2009/2010
95
Технологии расчетов
ÄÈÝËÜÊÎÌÅÒÐÈß
величинами
δu
Q
0
,
δu
Qε
;
—
коэффициент влияния, определяемый
коррелированными входными данными
Q
0ε
,
Q
00
. Коэффициенты влияния величин
u
i
= K
1
E
,
Q
0ε
,
Q
00
,
η
будут
С
K
= –1,
C
Qε
= –(
Q
0
ε
K
1
E
tg
δ
)
–1
,
C
Q
0
=
η
(
Q
00
K
1
E
tg
δ
)
–1
,
C
η
= –
C
Q
0
(9)
Оценки для относительных неопре-
деленностей
δQ
0
ε
,
δQ
00
собственных
добротностей могут быть выражены
через неопределенности
δQ
ε
,
δQ
0
на-
груженных добротностей
Q
ε
, Q
0
и пол-
ных коэффициентов связи резонатора
с образцом
β
ε
и без образца
β
0
.
В таблице 3 приведены значения
коэффициентов влияния и результаты
измерений tg
δ
полуволновых образ-
цов с оценкой
U
tg
δ
по составляющим
неопределенности из таблицы 1.
Результаты численного модели-
рования при различных значениях
x
и
ε
1
показали, что неопределенность
U
tgδ
(
x, ε
1
) также имеет осциллирующий
характер по
x
, достигая минимумов
при
x = π
(2
q
+ 1)/2 и максимумов при
x = qπ
(рис. 7). Максимумы
U
tg
δ
(
x, ε
1
)
убывают с ростом
q
. Осцилляции
U
tg
δ
(
x, ε
1
) обусловлены осцилляциями
K
1
E
(
x
) (рис. 4), возрастающими с ростом
ε
1
. Коэффициент заполнения входит в
коэффициенты влияния множителем
K
1
E
и его максимумам соответствуют
минимумы
U
tg
δ
(
x, ε
1
). Это объясняется
большей концентрацией энергии в
образце и большими относительными
потерями энергии (большим измене-
нием добротности резонатора) в этом
случае, чем в минимумах
K
1
E
. С умень-
шением tg
δ
неопределенность его
измерения монотонно возрастает.
Часть экспериментальных иссле-
дований влияния ионизирующего из-
лучения на диэлектрические свойства
полиэтилена и фторопласта, а также
щелочно-галоидных кристаллов, с ис-
пользованием описанного метода,
приведена в [13, 14].
Таким образом, метод цилиндри-
ческого резонатора с колебанием
H
01p
при фиксированной частоте позволяет
получать высокую точность измерения
ε
и tg
δ
. Его достоинствами являются:
возможность измерений повышенных
значений tg
δ
, однозначность процеду-
ры измерений (отсутствие мешающих
резонансов, приводящих к ошибоч-
ным результатам) и возможность ис-
пользования генератора СВЧ с малой
перестройкой частоты, необходимой
только для измерения добротности
резонатора.
Таблица 3. Значения коэффициентов влияния и результаты измерения tg
δ
полуволновых образцов с оценкой расширенной неопределенности
δ
(tg
δ
) =
U
tg
δ
Материал
C
K
C
Q
0
ε
C
Q
00
Cη
C
C
tgδ
×10
4
δ
(tg
δ
), %
Полиэтилен высокого давления
-1
-2,16
1,16
-1,16
1,58
2,6
4
Кварцевое стекло КВ
-1
-6,15
5,15
-5,15
5,63
0,9
13
Керамика ВК-94 -1
-1
-1,87
0,87
-0,87
1,28
9,3
3,5
Керамика ВК-100 -1
-1
-30,1
29,1
-29,1
29,6
0,3
68
Литература
1. Bussey H.E., Morris D., Zaltsman E.B. //
IEEE Trans. Instrum. and Meas. 1974. V. IM-23.
N 3, September. P. 236.
2. Vanzura E.J., Geyer R.G., Janesic M.D. //
NIST Technical Note 1354, 1993. P. 236.
3. Ni E., Stumper U. //Proc. IEEE. 1985.
V.132. Pt. 4. N 1.
4. Cook R.J.//Proc. Conf. «IPC Sci. and
Tech.»1973. P. 12.
5. Публикация МЭК 377-2-77.
6. ГОСТ 27496.2-87 Материалы электро-
изоляционные. Методы определения диэ-
лектрических свойств на частотах свыше
300 МГц. Резонансные методы.
7. ГОСТ 8.544-86. ГСИ. Относительная
диэлектрическая проницаемость и тангенс
угла диэлектрических потерь твердых диэ-
лектриков. Методика выполнения измере-
ний в диапазоне частот 109 — 1010 Гц.
8. ГОСТ Р 8.623-2006. ГСИ. Относитель-
ная диэлектрическая проницаемость и
тангенс угла диэлектрических потерь твер-
дых диэлектриков. Методики выполнения
измерений в диапазоне сверхвысоких ча-
стот.
9. Егоров В.Н., Кащенко М.В. // Измери-
тельная техника. 2002. №1, С. 61—65.
10. Руководство по выражению нео-
пределенности. СПб.: ВНИИМ, 1999.
11. Егоров В.Н., Кащенко М.В., Онхо-
нов Р.Р. // Измерительная техника. 2003.
№10, С. 41—45.
12. Егоров В.Н. // Приборы и техника
эксперимента. 2007. № 2. С. 5—38.
13. Романов Б.С., ЕгоровВ.Н., Костро-
мин В.В., Попов М.Ф. // Сб. «Вопросы
атомной науки и техники», сер. «Физика
радиационного воздействия на радиоэлек-
тронную аппаратуру», вып. 1—2, М.; 2006,
С. 87—90.
14. Егоров В.Н., Костромин В.В., Рома-
нов Б.С. // Сб. «Радиационная стойкость
электронных систем». СТОЙКОСТЬ. 2006.
вып. 9. М.: МИФИ. С.173—174.
Оригинал статьи: Метод объемного цилиндрического резонатора H01p для исследования диэлектриков на СВЧ
О достоинствах и преимуществах метода рассказывают специалисты ФГУП «ОКБ КП».











