Оригинал статьи: Метод контроля усталостного повреждения провода воздушной линии в процессе ее эксплуатации
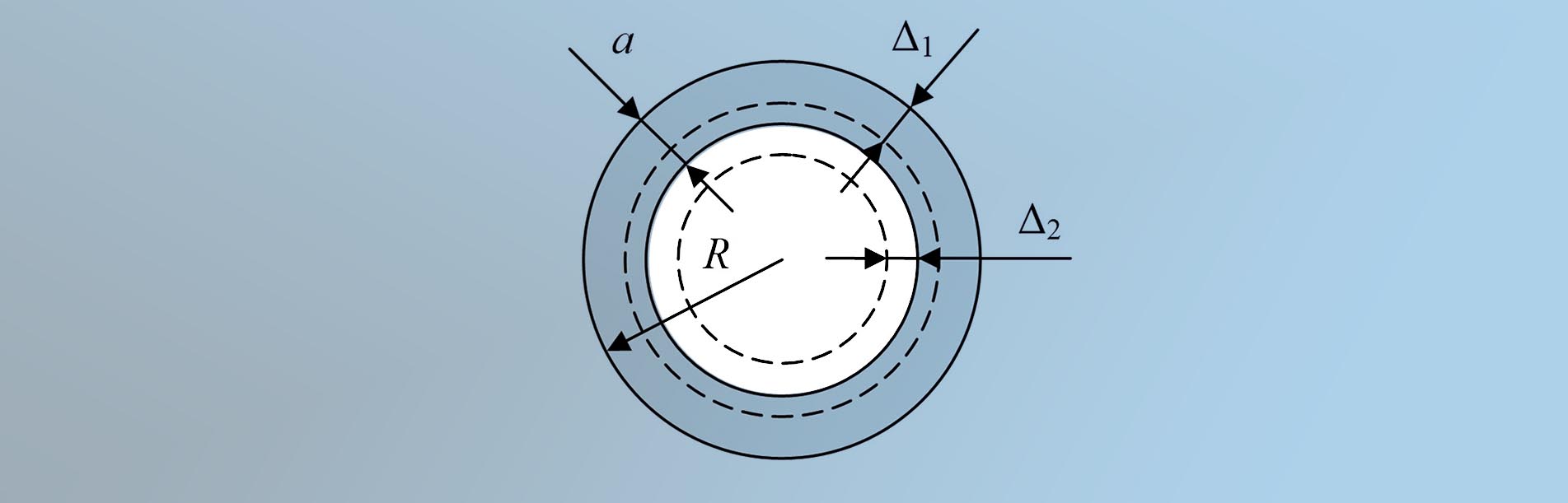
Провода воздушной линии передачи подвержены действию различных вредных факторов, среди которых значительную роль играют ветровые нагрузки. Под их воздействием возникают колебания и вибрация провода. В процессе эксплуатации в поверхностном слое накапливаются дефекты структуры металла провода. Степень развития усталостных повреждений определяется толщиной такого слоя. С целью контроля состояния провода предлагается измерять его поверхностную проводимость на высоких частотах. Решается задача определения глубины проникновения поля в двухслойной поверхностной структуре в зависимости от частоты и величины его проводимости. Толщина слоя определяется графическим методом. Такая методика может использоваться при определении толщины модифицированного слоя, возникающего при технологических операциях поверхностной обработки металлических деталей.