Механический расчет провода

46

ВОЗДУШНЫЕ

ЛИНИИ

Механический расчет провода

УДК

 621.315.1

На

сегодняшний

день

единственной

отечественной

 «

законной

» 

методикой

механиче

-

ского

расчета

проводов

и

тросов

являются

 «

Руководящие

указания

по

расчету

проводов

и

тросов

воздушных

линий

электропередачи

», 

утвержденные

 11 

августа

 1964 

года

, 

в

ко

-

торых

указано

: «

настоящие

РУ

составлены

в

предположении

, 

что

провода

и

тросы

подве

-

шены

на

одинаковых

высотных

отметках

, 

и

не

распространяется

на

особые

случаи

рас

-

чета

проводов

и

тросов

 (

открытые

распределительные

устройства

, 

большие

переходы

, 

участки

трассы

ВЛ

с

сильно

пересеченным

профилем

и

т

.

п

.)». 

По

мнению

автора

, 

пред

-

лагаемый

в

статье

метод

может

стать

основой

универсальной

точной

методики

механи

-

ческого

расчета

проводов

, 

тросов

, 

ВОК

всех

типов

для

любых

условий

. 

Мищенко

В

.

В

., 

главный

инженер

проекта

отдела

электротехнического

оборудования

АО

 «

Ленгидропроект

»

Ключевые

слова

: 

воздушные

линии

электропередачи

, 

механический

расчет

провода

, 

расчетная

схема

, 

гибкая

нить

Ц

ель

механического

расчета

про

-

вода

 — 

обеспечение

требований

нормативных

документов

 [1] 

при

работе

провода

в

нормальном

и

аварийном

режимах

. 

Выделяются

три

основные

задачи

расчета

: 

а

) 

установле

-

ние

формы

кривой

провисания

; 

б

) 

опре

-

деление

положения

произвольной

точки

этой

кривой

; 

в

) 

определение

тяжения

в

произвольной

точке

провода

 [2].

Первая

задача

давно

и

однозначно

решена

: 

провод

постоянного

сечения

, 

нагруженный

равномерно

распределен

-

ной

по

его

длине

нагрузкой

  (

например

, 

собственным

весом

), 

провисает

в

соот

-

ветствии

с

уравнением

цепной

линии

.

Уравнение

цепной

линии

в

системе

координат

 (

рисунок

 1) 

с

началом

в

вер

-

шине

кривой

 (

точке

 0) 

хорошо

известно

:

T

o 

p 

∙

 x

z

(

x

) = 

ch

 – 1

, (1)

p

T

o

где

T

o

 — 

тяжение

в

нижней

точке

кривой

провисания

  (

в

вершине

цепной

линии

); 

p

 — 

равномерно

распределенная

по

длине

провода

нагрузка

.

Тяжение

в

точке

провода

, 

имеющей

абсциссу

 x, 

можно

определить

по

про

-

стой

формуле

:

T

(

x

) = 

T

o

 + 

p

∙

z

(

x

). (2)

Представленные

выше

формулы

 (1) 

и

 (2) 

должны

закрыть

оставшиеся

две

задачи

: 

определение

положения

и

тяже

-

ния

в

произвольной

точке

провода

, … 

но

«

дьявол

кроется

в

деталях

». 

ОСОБЕННОСТИ

СУЩЕСТВУЮЩИХ

МЕТОДОВ

РАСЧЕТА

ПРОВОДА

Выражения

 (1) 

и

 (2) 

имеют

простой

вид

потому

, 

что

сформулированы

в

си

-

стеме

координат

, 

привязанной

к

верши

-

не

цепной

линии

 (

рисунок

 1). 

Положение

вершины

кривой

провисания

  (

точки

 0) 

в

отличие

от

точек

подвеса

 1 

и

 2, 

по

-

ложение

которых

заранее

известно

, 

не

поддается

фиксации

. 

При

изменении

состояния

провода

положение

вершины

кривой

провисания

постоянно

изменяет

-

ся

: 

происходит

смещение

точки

 0 

вдоль

цепной

линии

. 

В

отличие

от

точек

подве

-

са

 1 

и

 2, 

которые

остаются

теми

же

фи

-

зическими

точками

в

разных

состояниях

провода

, 

точка

 0 

для

двух

разных

состо

-

яний

провода

 — 

это

физически

разные

точки

, 

разнесенные

по

длине

провода

. 

Сформулируем

первую

особенность

следующим

образом

 — 

при

изменении

состояния

провода

отсутствует

гео

-

метрически

и

физически

постоянная

точка

отсчета

при

использовании

сис

-

темы

координат

, 

привязанной

к

верши

-

не

кривой

провисания

провода

.

Гиперболические

функции

, 

которые

используются

в

 (1) 

и

 (2), 

а

также

в

вы

-

текающих

из

них

формулах

, 

не

столь

распространены

в

инженерной

практи

-

ке

, 

как

тригонометрические

, 

степенные

или

логарифмические

функции

. 

Исполь

-

зование

гиперболических

функций

при

расчетах

сопряжено

с

определенными

вычислительными

трудностями

 — 

без

калькулятора

или

таблиц

трудно

оце

-

нить

 «

на

коленке

» 

то

или

иное

решение

. 

Современное

программное

обеспече

-

ние

позволяет

обойти

эту

проблему

, 

но

программа

не

развивает

, 

а

наоборот

притупляет

инженерную

интуицию

. 

Вто

-

рая

особенность

 — 

использование

ги

-

перболических

функций

в

явном

виде

не

позволяет

построить

интуитивно

по

-

нятную

для

большинства

инженеров

-

практиков

расчетную

модель

провода

.

В

этом

легко

убедиться

, 

обратившись

к

известной

монографии

Л

.

М

. 

Кесель

-

мана

 [2], 

в

которой

достаточно

подробно

изложена

методика

точного

расчета

про

-

вода

с

использованием

гиперболических

функций

.

Стремление

получить

вычислитель

-

но

простую

и

интуитивно

понятную

мето

-

47

Z

???

???

???

A

X

B

0

Рис

. 1. 

Система

координат

для

формул

 (1) 

и

 (2) 

привяза

-

на

к

вершине

цепной

линии

 (

точке

 0), 

положение

кото

-

рой

практически

не

фиксируется

дику

механического

расчета

провода

стало

причиной

развития

инженерного

метода

расчета

, 

подробно

разобранного

в

трудах

А

.

А

. 

Глазунова

, 

А

.

Д

. 

Бош

-

няковича

, 

К

.

П

. 

Крюкова

и

Б

.

П

. 

Новгородцева

 [3–5]. 

Инженерный

метод

построен

путем

введения

раз

-

ного

рода

  «

допущений

и

предположений

», 

которые

упрощают

исходные

формулы

точного

метода

рас

-

чета

провода

. 

За

простоту

расчетных

формул

при

-

ходится

платить

точностью

результатов

расчета

. 

В

большинстве

случаев

расчетная

погрешность

ин

-

женерного

метода

не

влияет

на

принятие

грамотного

проектного

решения

, 

о

чем

свидетельствуют

эпоха

массового

электросетевого

строительства

прошло

-

го

века

на

основе

инженерного

  (

приближенного

) 

метода

. 

Но

в

настоящее

время

, 

в

период

широкого

распространения

доступных

математических

про

-

грамм

, 

применение

приближенных

методов

расчета

, 

особенно

на

сложных

объектах

 (

большие

переходы

, 

горные

линии

, 

многоуровневые

пересечения

) 

можно

считать

необоснованным

  (

экстенсивным

) 

способом

капитального

строительства

. 

Инженерный

  (

прибли

-

женный

) 

метод

расчета

провода

, 

реализованный

в

отечественных

системах

автоматизирован

-

ного

проектирования

  (

САПР

) 

воздушных

линий

, 

не

соответствует

современному

уровню

раз

-

вития

вычислительной

техники

и

программного

обеспечения

. 

Существует

зарубежный

САПР

 [6], 

который

поз

-

воляет

численным

способом

найти

точное

решение

задач

механического

расчета

провода

. 

В

указанном

САПР

реализовано

несколько

расчетных

уровней

моделирования

провода

: 

первый

уровень

реализу

-

ет

метод

 «

приведенного

пролета

», 

на

остальных

 — 

метод

конечных

элементов

 (

МКЭ

). 

В

руководстве

по

использованию

 [6] 

указано

, 

что

большинство

практи

-

ческих

задач

решается

на

первом

 (

основном

) 

уров

-

не

, 

то

есть

с

использованием

метода

 «

приведенного

пролета

». 

Реализующие

МКЭ

уровни

не

получили

широкого

распространения

из

-

за

кажущейся

слож

-

ности

 [6, c. 146–147]. 

Отечественные

пользователи

данного

САПР

часто

не

подозревают

, 

что

их

резуль

-

тат

получен

инженерным

  (

приближенным

) 

методом

расчета

провода

, 

аналогичным

реализованному

в

отечественном

САПР

. 

В

инструкции

 [6, 

приложе

-

ние

 N] 

дано

небольшое

по

объему

и

слишком

общее

описание

МКЭ

, 

на

основании

которого

трудно

понять

и

тем

более

воспроизвести

способ

реализации

МКЭ

в

данной

САПР

. 

Зарубежный

САПР

 [6], 

реализую

-

щий

МКЭ

, 

применяется

  «

вслепую

»: 

пользователь

решает

большинство

задач

инженерными

  (

при

-

ближенными

) 

методами

, 

а

в

случае

использования

МКЭ

результат

не

верифицируется

, 

то

есть

его

нельзя

проверить

другими

точными

методами

расчета

.

Еще

одной

особенностью

существующих

мето

-

дов

расчета

провода

является

отсутствие

едино

-

го

и

однозначного

понятия

  «

исходное

» 

состояние

провода

. 

В

зарубежной

 (

американской

) 

практике

это

выражается

в

необходимости

выполнять

механиче

-

ский

расчет

провода

, 

исходя

из

трех

условных

его

состояний

: «

начальное

», «

после

нагрузки

», «

после

вытяжки

» [6]. 

В

отечественной

практике

аналогичная

неопределенность

с

 «

исходным

» 

состоянием

прово

-

да

проявляется

в

необходимости

поиска

критических

пролетов

, 

исходя

из

его

состояния

при

среднегодо

-

вой

температуре

, 

при

наибольшей

нагрузке

и

мини

-

мальной

температуре

 [2–5].

ИСХОДНОЕ

СОСТОЯНИЕ

«

МОНТАЖНОЕ

» 

(

ФИКСАЦИЯ

ДЛИНЫ

ПРОВОДА

В

ЗАЖИМАХ

)

Исторически

сложилось

, 

что

в

качестве

 «

исходно

-

го

» 

состояния

выбирается

одно

из

состояний

, 

при

ко

-

тором

напряжения

в

проводе

достигают

максималь

-

ных

значений

либо

провод

имеет

максимальную

стрелу

провеса

. 

Соответствующие

проектные

задачи

поиска

 «

критических

» 

пролетов

и

 «

критических

» 

тем

-

ператур

решены

А

.

А

. 

Глазуновым

 [3]. 

Нахождение

«

критических

» 

пролетов

 — 

основа

систематического

расчета

провода

 «

Руководящих

указаний

по

расчету

проводов

и

тросов

воздушных

линий

электропереда

-

чи

», 

упомянутых

в

аннотации

статьи

.

Использование

в

качестве

 «

исходного

» 

одного

из

предельных

состояний

провода

 — 

максимального

напряжения

или

максимального

провиса

 — 

явля

-

ется

идеальной

схемой

и

часто

не

отражает

реаль

-

ную

ситуацию

подвеса

провода

с

промежуточным

«

монтажным

» 

значением

тяжения

. «

Монтажное

» 

тяжение

должно

быть

достаточным

для

соблюдения

габаритов

до

земли

или

пересекаемого

препятствия

при

максимальном

провисе

провода

. 

При

этом

мак

-

симальные

напряжения

в

проводе

при

эксплуатации

не

должны

превышать

предельных

  (

нормативных

) 

значений

.

Для

поиска

  «

исходного

» 

состояния

провода

Л

.

М

. 

Кесельман

предложил

использовать

правило

наименьшего

напряжения



 [2, 

с

. 162]. 

Естествен

-

ным

развитием

этого

правила

стала

методика

вы

-

бора

исходного

режима

А

.

А

. 

Зевина

 [7]. 

В

предлага

-

емой

методике

вводится

понятие

  «

длина

заготовки

провода

», 

то

есть

длина

снятого

с

опор

провода

при

нулевых

напряжениях

и

температуре

. «

Длина

за

-

№

 2 (89) 2025

48

ВОЗДУШНЫЕ

ЛИНИИ

готовки

провода

» 

используется

как

промежуточная

величина

для

выбора

одного

из

  «

исходных

» 

со

-

стояний

провода

: 

при

среднегодовой

температу

-

ре

, 

минимальной

температуре

или

наибольшей

нагрузке

.

Развивая

идею

А

.

А

. 

Зевина

, 

предлагается

ис

-

пользовать

  «

длину

заготовки

провода

» 

не

как

вспомогательную

расчетную

, 

а

как

основную

ве

-

личину

, 

которая

и

определяет

исходное

состояние

провода

. 

Далее

в

статье

понятие

 «

длина

заготовки

прово

-

да

» (

Зевин

, 2009) 

заменяется

относительной

величи

-

ной

 — 

монтажным

удлинением

провода



m

, 

которую

трактуем

аналогично

 [7], 

то

есть

это

относительное

превышение

заготовки

провода

 (

длина

провода

при

нулевой

температуре

и

отсутствии

напряжений

) 

кратчайшего

расстояния

между

точками

ее

подвеса

в

пролете

. 

Монтажное

удлинение

провода



m

определяет

па

-

раметры

кривой

его

провисания

в

пролете

  (

цепной

линии

) 

и

задается

во

время

монтажа

при

фиксации

провода

в

креплениях

. 

Режим

провода

до

фиксации

его

длины

 (

при

свободном

его

перемещении

в

мон

-

тажных

роликах

) 

считается

монтажным

. 

После

фик

-

сации

 — 

эксплуатационным

.

ПАРАМЕТРИЧЕСКОЕ

УРАВНЕНИЕ

ЦЕПНОЙ

ЛИНИИ

Уравнение

 (1) 

определяет

положение

точек

цеп

-

ной

линии

в

явном

виде

, 

то

есть

координата

z

пред

-

ставляет

функцию

координаты

x

. 

Введем

параметр

 t 

следующим

образом

:

dz

p

∙

x

x

t

 = 

 = 

sh

 = 

sh

. (3)

dx

T

o

a

Согласно

 (3) 

параметр

t

 — 

тангенс

угла

наклона

касательной

к

цепной

линии

. 

Постоянная

цепной

линии

a

, 

равная

отношению

горизонтальной

состав

-

ляющей

тяжения

T

o

к

погонной

нагрузке

p

, 

имеет

размерность

  [

a

]=

м

, 

таким

образом

постоянная

a

 — 

величина

, 

определяющая

только

геометрию

кривой

провисания

провода

.

Уравнение

цепной

линии

 (1) 

с

использованием

 (3) 

перепишем

в

параметрическом

виде

, 

когда

коорди

-

наты

z

и

x

есть

функция

параметра

t

:

x

(

t

) = 

a

∙

ln

(

t

 + 

√

t

2

 + 1), 

(4

а

)

z

(

t

) = 

a

∙

(

√

t

2

 + 1 – 1). 

(4

б

)

Уравнения

 (1) 

и

 (4) 

описывают

геометрическое

по

-

ложение

точек

провода

в

системе

отсчета

с

началом

координат

в

вершине

цепной

линии

, 

то

есть

в

низ

-

шей

точке

провисания

провода

. 

Отмечено

ранее

, 

что

определить

низшую

точку

кривой

провисания

затруднительно

, 

а

иногда

невозможно

  (

например

, 

когда

провод

расположен

полностью

на

нисходящей

/

восходящей

ветви

цепной

линии

). 

При

изменении

состояния

провода

  (

температура

, 

нагрузка

) 

верши

-

на

кривой

провисания

меняет

геометрическое

по

-

ложение

и

физически

смещается

вдоль

провода

. 

Целесообразно

применять

постоянную

систему

от

-

счета

с

фиксированным

началом

координат

, 

напри

-

мер

в

одной

из

точек

крепления

провода

 (

рисунок

 2).

Пусть

t

a

 — 

значение

параметра

в

точке

A

, 

совпа

-

дающей

с

началом

отсчета

, 

тогда

параметрическое

уравнение

цепной

линии

примет

вид

:

x

(

t

) = 

a

∙

 [

ln

(

t

 + 

√

t

2

 + 1) – 

ln

(

t

a

 + 

√

t

a

2

 + 1)], 

(5

а

)

z

(

t

) = 

a

∙

 (

√

t

2

 + 1 – 

√

t

a

2

 + 1). 

(5

б

)

Если

ввести

криволинейную

координату

s

(

t

), 

от

-

меряемую

по

оси

гибкой

нити

от

точки

A

 (

рисунок

 2), 

то

геометрическая

длина

провода

L

AB

в

параметри

-

ческом

виде

определяется

простой

формулой

:

s

(

t

) = 

a

∙

 (

t

 – 

t

a

) = 

L

AB

. (6)

Тяжение

в

точке

провода

с

параметром

t

имеет

также

простой

вид

:

T

(

t

) = 

a

∙

p

∙

√

t

2

 + 1 = 

T

o

∙

√

t

2

 + 1. 

(7)

Перемещаясь

слева

направо

вдоль

кривой

про

-

висания

провода

значение

параметра

t

принимает

A

 — 

точка

крепления

провода

, 

начало

координат

системы

от

-

счета

B

 — 

произвольная

точка

цепной

линии

 (

например

, 

вторая

точка

крепления

)

Рис

. 2. 

Практическая

система

отсчета

для

задач

под

-

веса

гибкой

нити

x

(

t

)

T

(

t

)

t

B

Z(t)

z

x

S(t)

t

A

A

B

Рис

. 3. 

Расчетная

схема

расчета

провода

в

пролете

 12 

(

f

i

12

 — 

стрела

провеса

провода

в

произвольной

точке

i

)

x

12

 = 

x

2

 – 

x

1

1

t

1

t

2

t

12

t

 = 0

t

12

 = 

z

12

/

x

12

Z

12

 = 

Z

2

 – 

Z

1

t

i

f

i

12

i

f

max

12

f

o

12

2

0

49

значения

от

 –



до

 +



. 

На

кривой

провисания

, 

прохо

-

дящего

через

точки

крепления

провода

, 

имеются

две

характерные

точки

, 

значение

параметра

в

которых

известно

 (

рисунок

 3): 

t

o

 = 0 — 

нижняя

точка

кривой

провисания

  (

вершина

цепной

линии

); 

t

12

 = 



Z

/



X

 — 

точка

кривой

провисания

 c 

максимальной

стрелой

провеса

провода

в

пролете

длиной



X

и

разностью

высот

точек

крепления



Z

. 

РАСЧЕТНАЯ

СХЕМА

«

НЕРАСТЯЖИМАЯ

НИТЬ

»

Рассмотрим

подвеску

провода

между

двумя

не

-

подвижными

точками

 1 

и

 2. 

Взаимное

расположение

точек

крепления

задается

пролетом

X

12

и

тангенсом

угла

наклона

соединяющей

их

прямой

t

12

. 

Тогда

пре

-

вышение

точки

 2 

над

точкой

 1 

составит

Z

12

 = 

X

12

∙

t

12

, 

а

кратчайшее

расстояние

между

ними

 — 

b

12

  =

= 

X

12

∙

√

1 + 

t

12

2

  (

рисунок

 3).

Расчетная

схема

 «

нерастяжимая

нить

» 

предпола

-

гает

неизменную

длину

подвешенного

провода

, 

кото

-

рая

не

зависит

ни

от

растягивающих

усилий

в

про

-

воде

, 

ни

от

изменения

его

температуры

. 

Очевидно

, 

что

для

нерастяжимого

провода

относительное

его

удлинение



12

до

и

после

подвески

останется

посто

-

янным

и

равным

монтажному

удлинению



m

.

Механический

расчет

провода

по

схеме

  «

нерас

-

тяжимая

нить

» 

состоит

в

определении

параметров

кривой

провисания

провода

 — 

цепной

линии

, 

про

-

ходящей

через

точки

крепления

 1 

и

 2. 

Для

этого

не

-

обходимо

решить

систему

геометрических

уравне

-

ний

, 

связывающую

известные

величины

 (

пролет

X

12

, 

превышение

Z

12

и

длину

провода

L

12

 = 

b

12

∙

 (1 + 



m

)) 

с

искомыми

величинами

  (

постоянной

цепной

линии

a, 

параметрами

t

1

и

t

2

в

точках

крепления

провода

). 

Разрешающая

система

на

основе

параметрического

уравнения

цепной

линии

 (5) 

и

формулы

 (6) 

имеет

вид

:

X

12

 = 

a

∙

 [

ln

(

t

2

 + 

√

t

2

2

 + 1) – 

ln

(

t

1

 + 

√

t

1

2

 + 1)];

  X

12

∙

t

12

 = 

a

∙

 (

√

t

2

2

 + 1 – 

√

t

1

2

 + 1); 

(8)

b

12

∙

 (1 + 



m

) = 

a

∙

 (

t

2

 – 

t

1

). 

Система

 (8) 

не

требует

дальнейших

преобразо

-

ваний

, 

чтобы

найти

искомые

величины

. 

Для

ее

ре

-

шения

достаточно

воспользоваться

любым

матема

-

тическим

пакетом

со

встроенной

функцией

решения

систем

уравнения

. 

На

рисунке

 4 

дан

пример

решения

системы

уравнений

 (8) 

в

широко

распространенной

программе

 MathCad 

при

помощи

встроенной

функ

-

ции

fi

 nd

для

решения

уравнений

и

систем

уравнений

. 

Читатели

могут

самостоятельно

проверить

возмож

-

ность

быстрого

получения

расчетного

результата

без

до

-

полнительных

преобразований

уравнений

, 

а

также

вне

-

Рис

. 4. 

Пример

решения

системы

 (8) 

в

 MathCad

№

 2 (89) 2025

50

ВОЗДУШНЫЕ

ЛИНИИ

сения

 «

упрощений

и

допущений

» 

в

расчетную

схему

для

довольно

непростой

системы

уравнений

 (8), 

набрав

пред

-

ставленный

на

рисунке

 4 

пример

на

своем

персональном

компьютере

и

задавая

разные

значения

исходных

дан

-

ных

. 

Результат

впечатляет

своей

эффективностью

.

Получив

неизвестные

a

, 

t

1

и

t

2

для

заданных

исход

-

ных

данных

, 

можно

для

произвольной

точки

кривой

провисания

с

параметром

t

 (

t

1



t



t

2

) 

решить

задачи

, 

указанные

в

первом

абзаце

статьи

: 

определить

при

помощи

 (5) 

положения

точки

в

прямоугольной

системе

координат

с

началом

в

точке

 1; 

определить

при

помо

-

щи

 (6) 

положения

точки

в

криволинейной

системе

ко

-

ординат

, 

привязанной

к

проводу

с

началом

в

точке

 1; 

в

) 

определить

при

помощи

 (7) 

тяжение

в

проводе

. 

Подставив

в

 (5) 

значения

параметра

 0 

и

t

12

, 

полу

-

чим

для

данного

пролета

соответственно

положение

низшей

точки

провода

и

точки

с

максимальной

стре

-

лой

провеса

. 

РАСЧЕТНАЯ

СХЕМА

«

УПРУГОДЕФОРМИРУЕМЫЙ

ПРОВОД

»

После

подвески

провод

под

действием

продоль

-

ного

растягивающего

усилия

удлиняется

. 

На

длину

провода

также

влияет

его

фактическая

температура

. 

Относительное

удлинение

провода



12

после

подвес

-

ки

представляет

собой

сумму

монтажного



m

и

упру

-

гого

удлинения

, 

вызванного

тяжением



T

и

измене

-

нием

температуры





. 

Длина

упругодеформируемого

провода

после

подвески

: 

L

12

 = 

b

12

∙

 (1 + 



m

 + 



T

 + 





) = 

a

∙

 (

t

2

 – 

t

1

). (9)

Обозначим

расчетные

характеристики

провода

следующим

образом

: 

q

 — 

собственный

вес

; 



 — 

температурный

коэффициент

линейного

удлинения

; 

EF

 — 

жесткость

провода

на

осевое

растяжение

, 

ко

-

торая

находится

как

произведение

модуля

упругости

провода

на

площадь

его

поперечного

сечения

. 

Под

-

вешенный

провод

испытывает

климатические

воз

-

действия

, 

характеризуемые

величинами

: 



 — 

тем

-

пература

провода

и



p

 — 

дополнительная

нагрузка

, 

обобщающая

ветровое

и

гололедное

воздействие

. 

Относительное

изменение

длины

провода

под

действием

температуры

и

тяжения

составят

соот

-

ветственно

: 





 = 



∙



и



T

 = 

T

12

 / 

EF

, (10)

где

T

12

 — 

действующее

тяжение

— 

фиктивная

ве

-

личина

тяжения

, 

равномерно

распределенная

по

длине

провода

, 

относительное

удлинение

под

дей

-

ствием

которого

будет

равно

действию

фактическо

-

го

неравномерного

по

длине

провода

тяжения

 [8]. 

В

приближенных

методах

расчета

вместо

действую

-

щего

тяжения

принимается

либо

тяжение

в

нижней

точке

провода

, 

либо

среднее

между

минимальным

и

максимальным

значениями

тяжения

. 

Значение

действующего

тяжения

определяется

по

формуле

:

T

12

 = 

a

∙

 (

q

 + 



p

) 



t

2

 + 

√

t

2

2

 + 1

t

2

∙

√

t

2

2

 + 1 – 

t

1

∙

√

t

1

2

 + 1 + 

ln 

t

1

 + 

√

t

1

2

 + 1





. 

(11)

 2 

∙

 (

t

2

 – 

t

1

) 

Формула

 (11) 

имеет

довольно

 «

грозный

» 

вид

, 

ана

-

логичный

формулам

точного

расчета

в

 [2]. 

Но

, 

в

отли

-

чие

от

 [2], 

это

единственная

 «

громоздкая

» 

формула

, 

которая

при

этом

легко

реализуется

в

виде

встро

-

енной

функции

и

не

влияет

на

производительность

MathCad 

при

численном

решении

разрешающей

сис

-

темы

уравнений

, 

а

также

на

сходимость

результата

. 

Система

 (8) 

для

нерастяжимой

нити

объединяет

три

геометрических

уравнения

. 

При

переходе

к

рас

-

четной

схеме

  «

упругодеформируемого

провода

» 

в

системе

 (8), 

составленной

для

схемы

  «

нерастя

-

жимого

провода

», 

последнее

геометрическое

урав

-

нение

должно

быть

заменено

на

физическое

урав

-

нение

 (9), 

описывающее

упругое

деформирование

провода

под

нагрузкой

. 

Температурные

деформации

относятся

к

упругим

, 

так

как

они

исчезают

при

нуле

-

вой

температуре

. 

Подставляя

 (10) 

в

уравнение

 (9), 

а

также

добавляя

уравнение

 (11), 

получим

разреша

-

ющую

систему

для

упругодеформируемого

провода

: 

  X

12

 = 

a

∙

 [

ln

(

t

2

 + 

√

t

2

2

 + 1) – 

ln

(

t

1

 + 

√

t

1

2

 + 1)];

  X

12

∙

t

12

 = 

a 

∙

 (

√

t

2

2

 + 1 – 

√

t

1

2

 + 1);

  b

12

∙

 (1 + 



m

 + 



∙



 + 

T

12

 / 

EF

) = 

a

∙

 (

t

2

 – 

t

1

);

  T

12

 = 

a

∙

 (

q

 + 



p

) 



t

2

 + 

√

t

2

2

 + 1

t

2

∙

√

t

2

2

 + 1 – 

t

1

∙

√

t

1

2

 + 1 + 

ln 

t

1

 + 

√

t

1

2

 + 1

 

. 

(12)

 2 

∙

 (

t

2

 – 

t

1

) 

Система

уравнений

 (12) 

также

легко

решается

при

помощи

математической

программы

 MathCad 

с

использованием

встроенной

функции

fi

 nd

, 

предна

-

значенной

, 

в

том

числе

, 

для

решения

систем

нели

-

нейных

уравнений

. 

Примеры

решения

системы

 (12), 

аналогичные

представленному

на

рисунке

 4 

реше

-

нию

системы

 (8), 

не

приводятся

из

-

за

ограниченного

объема

статьи

.

ПРЯМАЯ

, 

МОНТАЖНАЯ

И

ОБРАТНАЯ

ЗАДАЧИ

МЕХАНИЧЕСКОГО

РАСЧЕТА

Система

уравнений

 (12) 

определяет

напряженно

-

деформированное

состояние

провода

в

любом

его

состоянии

: 

при

температуре



и

дополнительной

нагрузке



p

. 

Разрешающая

система

уравнений

 (12) 

сформулирована

без

введения

 «

допущений

и

упро

-

щений

», 

что

характерно

для

инженерных

  (

прибли

-

женных

) 

методов

механического

расчета

провода

. 

Решение

данной

системы

не

содержит

погрешно

-

стей

, 

связанных

с

введением

 «

допущений

и

упроще

-

ний

», 

приводящих

 (12) 

к

классическому

уравнению

состояния

провода

в

виде

кубического

уравнения

 [9].

Систему

 (12) 

можно

условно

назвать

 «

уравнени

-

ем

состояния

провода

» 

в

точной

формулировке

. 

Как

было

отмечено

ранее

, 

исходное

состояние

провода

характеризует

относительная

величина



m

 — 

мон

-

тажное

удлинение

провода

. 

Задаваясь

значением



m

, 

через

решение

системы

 (12) 

можно

определить

напряженно

-

деформированное

состояние

провода

при

любом

его

состоянии

: 

параметры

цепной

a

, 

t

1

и

t

2

однозначно

определяют

по

формуле

 (5) 

положение

всех

точек

провода

в

пролете

, 

а

тяжение

в

нем

 — 

по

формуле

 (7). 

Используя

параметры

a

, 

t

1

и

t

2

, 

можно

51

решить

все

практические

задачи

: 

проверку

прочно

-

сти

провода

в

точках

подвеса

, 

определение

стрел

провеса

провода

, 

определение

габаритов

от

провода

до

земли

и

пересекаемых

препятствий

 [10].

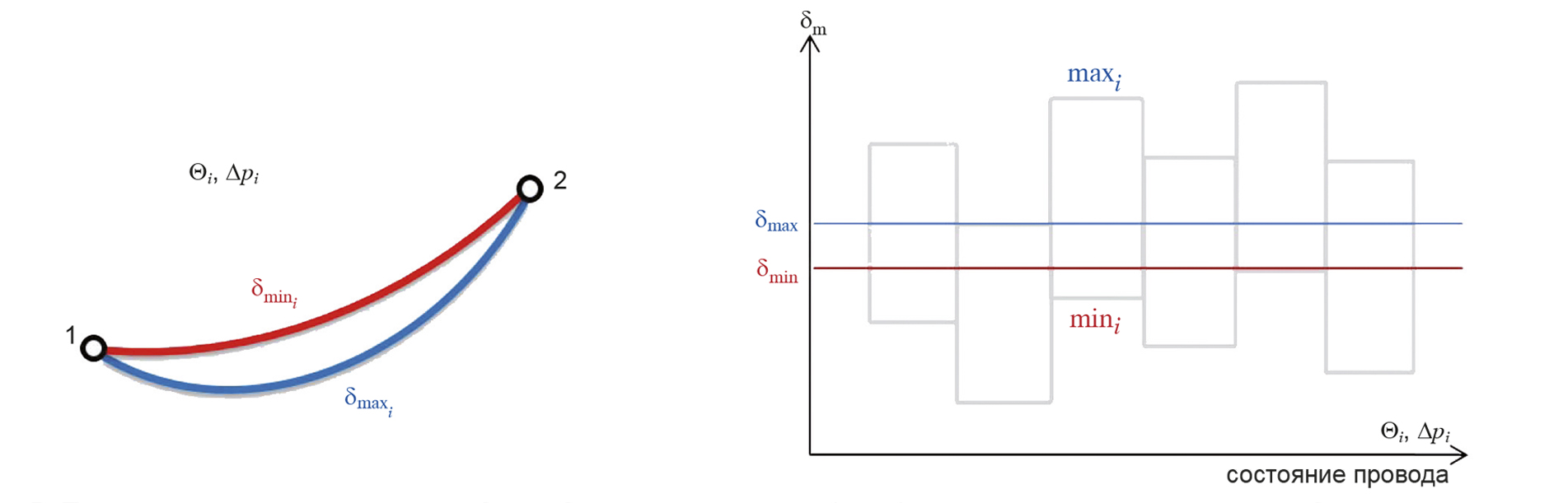
Изменяя

монтажное

удлинение

провода



m

, 

при

решении

системы

 (12) 

получим

разные

значения

па

-

раметров

a

, 

t

1

и

t

2

, 

которые

в

свою

очередь

определя

-

ют

разные

кривые

провисания

провода

. 

В

наиболее

общем

случае

для

заданного

состояния

провода

(

заданы

температура

и

дополнительная

нагрузка

на

провод

) 

механический

расчет

провода

заключа

-

ется

в

определении

параметров

двух

кривых

про

-

висания

: 

прочностной

и

габаритной

(

рисунок

 5). 

Верхняя

прочностная

кривая

, 

которая

на

рисунке

 5 

показана

красным

цветом

, 

соответствует

условию

максимально

допустимого

натяжения

провода

по

условию

его

прочности

в

верхней

точке

крепления

; 

в

этом

случае

длина

монтажной

заготовки

провода

, 

а

значит

относительного

монтажного

удлинения



m

имеют

минимальные

значения

 (

чем

короче

провод

, 

тем

сильней

тяжение

). 

Тяжение

в

нижней

кривой

на

рисунке

 5 

ослаблено

по

отношению

к

вышележа

-

щим

кривым

, 

поэтому

габаритная

кривая

 (

синяя

на

рисунке

 5) 

имеет

максимальное

монтажное

удлине

-

ние

. 

Если

при

эксплуатации

провода

заданное

со

-

стояние

 (



, 



p

) 

сохранялось

постоянным

, 

то

подвес

-

ку

провода

можно

выполнять

с

любым

монтажным

удлинением

: 



мин





m





макс

. (13)

Состояние

провода

в

процессе

эксплуатации

из

-

меняется

. 

Нормами

 [1] 

задается

ряд

предельных

климатических

состояний

, 

при

которых

в

подвешен

-

ном

пролете

должны

быть

соблюдены

нормативные

требования

по

прочности

провода

и

габаритам

его

приближения

к

земле

, 

сторонним

объектам

и

соору

-

жениям

. 

Область

фактически

возможного

монтаж

-

ного

удлинения

провода

представляет

собой

пере

-

сечение

множеств

 (13) 

для

отдельных

нормативных

состояний

провода

. 

На

рисунке

 5 

эта

область

рас

-

полагается

между

двумя

прямыми

. 

В

идеальном

случае

множество

 (13) 

может

быть

представлено

единственным

числом

, 

например

когда

опоры

на

профиле

расставлены

строго

по

габаритному

шаб

-

лону

, 

построенному

для

предельно

допускаемо

-

го

тяжения

. 

Ситуация

, 

когда

 (13) 

представляет

со

-

бой

пустое

множество

, 

говорит

о

том

, 

что

подве

-

сить

провод

с

соблюдением

всех

требований

норм

в

данном

пролете

не

представляется

возможным

.

Выбранное

при

проектировании

и

зафиксирован

-

ное

при

строительстве

значение

монтажного

удлине

-

ния

провода



m

является

инвариантом

технического

решения

, 

который

определяет

дальнейшее

поведе

-

ние

провода

после

монтажа

во

всех

возможных

его

состояниях

. 

Монтаж

провода

, 

при

котором

фиксируется

его

длина

в

пролете

, 

выполняется

при

разных

темпера

-

турах

воздуха

и

, 

соответственно

, 

провода

. 

Появля

-

ется

необходимость

в

монтажных

таблицах

, 

которые

определяют

возможные

состояние

провода

при

мон

-

таже

из

-

за

изменения

его

температуры

. 

Очевидно

, 

что

монтажные

таблицы

не

нужны

, 

если

монтаж

про

-

вода

всегда

выполнялся

только

при

нулевой

темпе

-

ратуре

. 

Тогда

единственные

значения

стрелы

прове

-

са

и

тяжения

зависят

только

от

упругой

деформации

из

-

за

растяжения

провода

под

нагрузкой

. 

Монтажное

удлинение

провода



m

при

проектиро

-

вании

не

задается

. 

Косвенно

ее

значение

задается

допускаемым

напряжением

в

проводе

при

одном

из

состояний

провода

: 

при

среднегодовой

температуре

, 

минимальной

температуре

или

наибольшей

нагруз

-

ке

. 

По

выбранному

допускаемому

напряжению

, 

ис

-

пользуя

классическое

уравнение

состояния

провода

, 

рассчитывают

монтажные

таблицы

. 

Из

-

за

наличия

неучтенных

систематических

погрешностей

приме

-

нение

монтажных

таблиц

, 

полученных

инженерными

(

приближенными

) 

методами

расчета

, 

не

всегда

кор

-

ректно

: 

на

больших

переходах

, 

горных

линиях

, 

жест

-

ких

ограничениях

по

габаритам

приближения

и

т

.

д

. 

Монтажные

таблицы

, 

отражающие

фактическое

поведение

провода

во

всех

возможных

случаях

мон

-

тажа

, 

рассчитываются

при

заданном

монтажном

удлинении

точным

методом

, 

используя

систему

уравнений

 (12).

Задачи

определения

напряженно

-

деформиро

-

ванного

состояния

уже

подвешенных

проводов

, 

также

легко

решаются

с

использованием

системы

уравнений

 (12). 

Для

этого

предварительно

опреде

-

ляется

монтажное

удлинение

уже

подвешенного

провода

по

результатам

дополнительных

замеров

одним

из

известных

способов

  (

стрелы

провеса

, 

положения

промежуточной

точки

, 

тяжения

в

точке

Рис

. 5. 

Положение

кривых

провисания

для

заданного

состояния

 (



, 



p

) 

при

изменении

монтажного

удлинения



m

заготовки

провода



i

, 



p

i



i

, 



p

i

1

2



min

i



m



min

min

i



max

i



max

max

i

состояние

провода

№

 2 (89) 2025

52

ВОЗДУШНЫЕ

ЛИНИИ

крепления

и

т

.

д

.). 

Для

нахождения

неизвестного

значения



m

система

 (12) 

дополняется

одним

или

двумя

уравнениями

, 

включающими

замеренные

параметры

. 

Численное

решение

новой

системы

выполняется

аналогично

представленному

ранее

(

рисунок

 4). 

Все

задачи

механического

расчета

провода

на

основе

монтажного

удлинения

провода

и

с

приме

-

нением

параметрического

уравнения

цепной

линии

можно

разделить

на

три

типа

: 

прямые

, 

монтажные

и

обратные

 (

рисунок

 6). 

УЧЕТ

ВЫТЯЖКИ

ПРОВОДА

ПРИ

МЕХАНИЧЕСКОМ

РАСЧЕТЕ

В

процессе

навивки

на

барабан

провод

дефор

-

мируется

: 

приобретает

кривизну

. 

Криволинейное

положение

провода

после

снятия

с

барабана

и

при

отсутствии

осевого

усилия

определяется

возникши

-

ми

в

процессе

навивки

остаточными

деформациями

материала

провода

. 

Остаточные

неупругие

деформации

, 

получен

-

ные

в

процессе

навивки

, 

задают

некую

начальную

кривизну

провода

. 

При

монтаже

под

действием

про

-

дольного

усилия

 (

тяжения

) 

происходит

уменьшение

его

остаточной

кривизны

 — 

провод

выпрямляет

-

ся

после

обработки

монтажным

тяжением

. 

Макси

-

мальные

эксплуатационные