Использование обобщенных параметров схемы для оценки и ограничения токов короткого замыкания сложных электроэнергетических систем

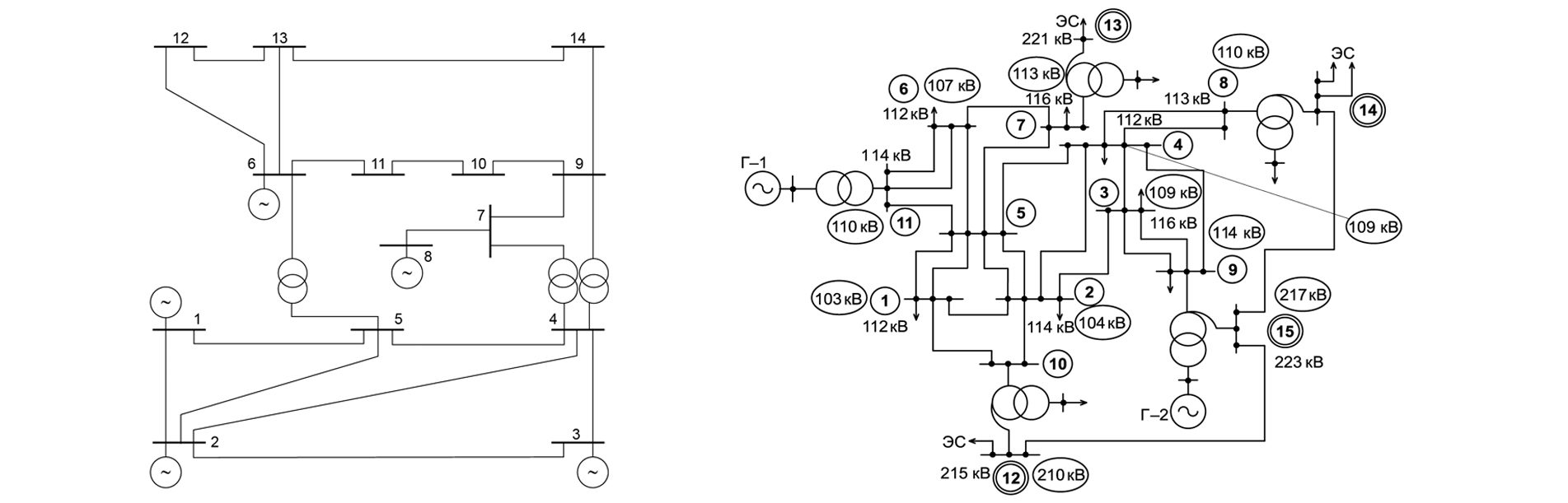
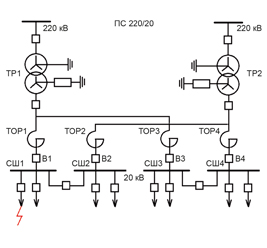
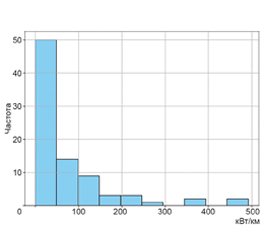
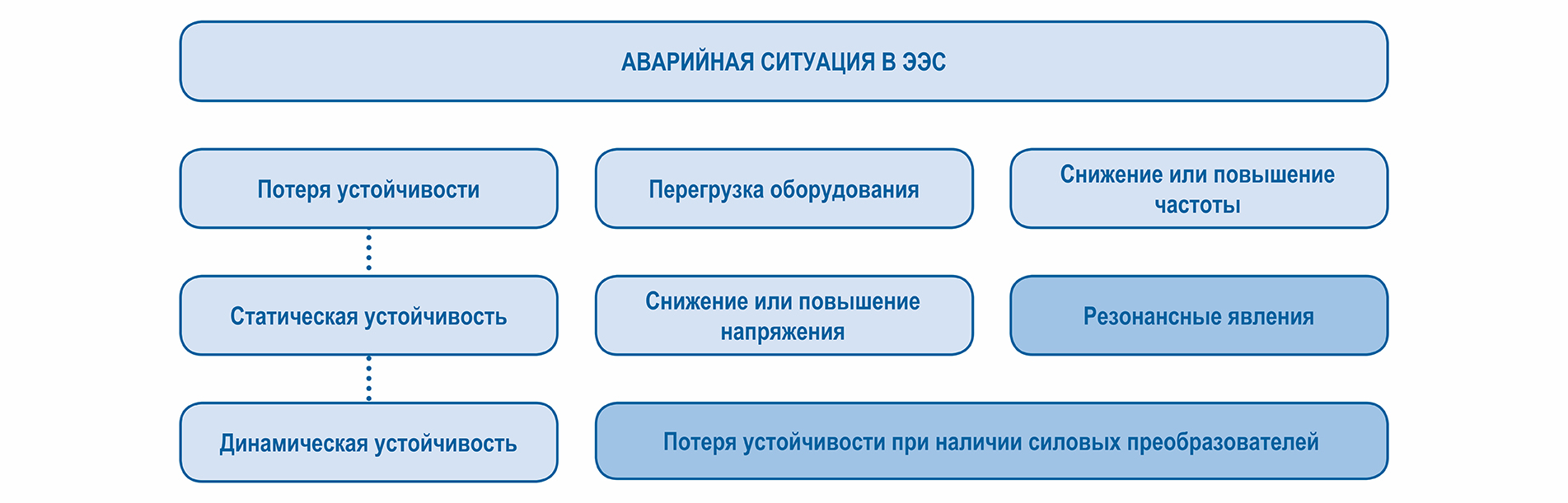
Исследуется актуальная проблема ограничения токов короткого замыкания в сложных электроэнергетических сетях с распределенной генерацией при неполноте исходных данных. При этом для оценки нечувствительности исследуемых узлов к возмущениям предлагается использование обобщенных параметров схемы электрической сети на базе метода сальдо-проводимости. Посредством проведения сингулярного анализа в работе доказывается эффективность предлагаемой методики. Также разработаны математические модели интервальной оценки величины токов короткого замыкания в узлах сети на примере региональной электроэнергетической системы 110 кВ, ранжированных по степени их нечувствительности к возмущениям.