
Глава 3. Математические модели ПЭУ
73
Глава третья
МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПЭУ
3.1. Математические модели режимов работы АД
в составе ПЭД ПЭУ
Классификация ЭФВ, рассмотренная выше, констатирует их комплекс-
ное воздействие на элементы ПЭУ и позволяет выделить среди них значи-
тельную часть, определяемую электромагнитными и электромеханическими
процессами. При этом их статическому и динамическому влиянию наиболь-
шим образом подвержены электромеханические устройства в составе ПЭУ
и именно ПЭД. Проведенный анализ известных работ [8–11, 13, 21, 22],
результаты настоящего исследования и данные эксплуатации подтверждают,
что самым ненадежным элементом ПЭУ является ПЭД. Классическое
и наиболее распространенное исполнение ПЭД – асинхронный электродви-
гатель (АД).
Режимы работы АД в составе ПЭД (далее ПЭД(А)) исследовались в ряде
работ [16, 17, 20, 23], однако после подробного анализа можно отметить недос-
таточную освещенность проблемы моделирования различных динамических
режимов работы ПЭД(А) под воздействием комплекса ЭФВ. Это прежде всего
связано с определением реакции изменения параметров установки под воздей-
ствием моделируемых ЭФВ, которое для обеспечения надежности действующе-
го оборудования должно быть реализовано в математической модели (ММ)
динамического нагружения.
Широко используются модели, в основу которых положены уравнения
Парка – Горева [24, 25]. Но в большинстве этих моделей не учитывается ряд
физических явлений, в частности явление вытеснения тока, потери в стали,
насыщение магнитной системы и т. д. Это приводит к значительным погреш-
ностям расчетов при реализации ММ ПЭД(А). Однако ММ Парка – Горева
служат основой для изучения, расширения знаний, совершенствования ММ
ПЭД(А) [26], а также проектирования и эксплуатации ПЭУ.
Отметим, что при моделировании ММ ПЭД(А) важное место занимает
принятое формирование начальных условий и исходных данных. Как прави-
ло, это параметры схемы замещения ПЭД(А), которые определяются слагае-
мыми, зависящими от напряжения, нагрузки, частоты, температуры электро-
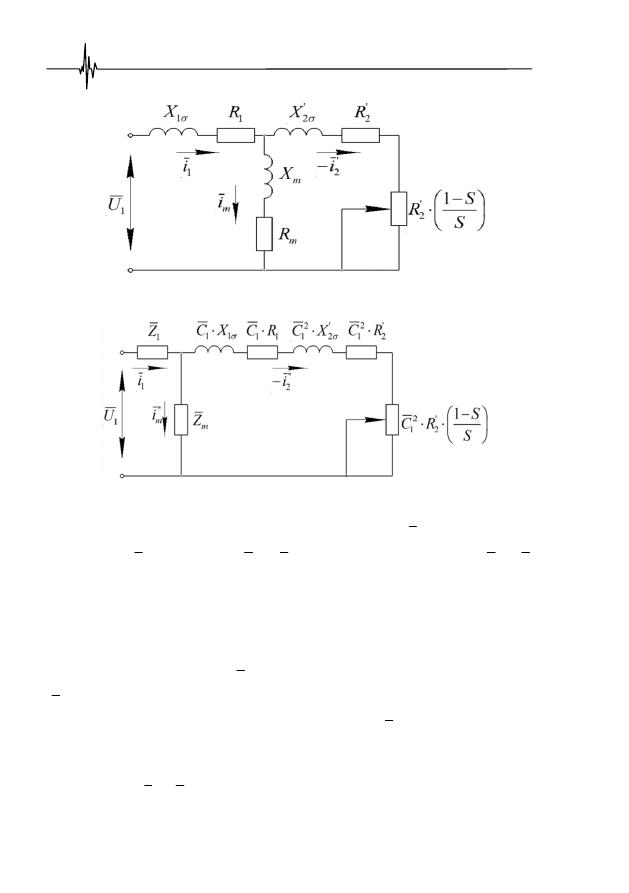
двигателя. Они формируются на одну фазу (рис. 3.1, 3.2) «Т-образной» или
«Г-образной» схемами замещения ПЭД(А) [27].
Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
74
Рис. 3.1.
Т-образная схема замещения ПЭД(А)
Рис. 3.2.
Г-образная схема замещения ПЭД(А)
Приняты следующие обозначения и сокращения:
– фазное напряже-
ние статора; – ток статора;
и
– приведенные токи ротора;
и
–
токи цепи намагничивания;
– активное сопротивление и индуктивное
сопротивление рассеяния статорной обмотки;
– приведенные к ста-
торной обмотке активное сопротивление и индуктивное сопротивление рас-
сеяния роторной обмотки;
– активное и индуктивное сопротивления
намагничивающего контура;
– полное сопротивление фазы обмотки статора;
– полное сопротивление цепи намагничивания;
– переменное
активное сопротивление, зависящее от скольжения;
– коэффициент приве-
дения «Т-образной» к «Г-образной» схеме замещения.
Далее также используются величины, сопряженные с обозначенными ра-
нее, а именно: и
– ЭДС фаз статора и ротора соответственно;
–
синхронная частота вращения поля статора; – число пар полюсов статорной
1
U
1
i
'
2
i
''
2
i
m
i
''
m
i
1
1
,
x
R
'
'
2
2
,
x
R
,
m
m
x
R
1
Z
m
Z
'
2
(1
) /
R
S
S
1
C
1
e
2
e
2
pf
p
Глава 3. Математические модели ПЭУ
75
обмотки;
и
– векторы потокосцеплений статора и ротора соответст-
венно;
и
– индуктивности статорной и роторной обмотки соответст-
венно.
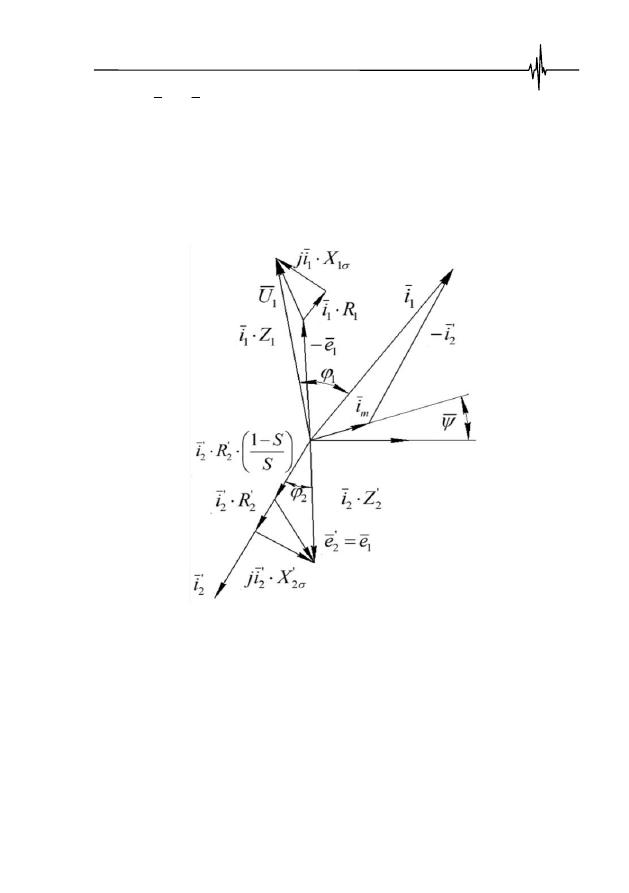
На рис. 3.3 и 3.4 приведены векторная диаграмма рабочего режима
ПЭД(А), соответствующая Т-образной схеме замещения, и зависимости
изменения параметров ПЭД(А) в различных режимах работы под воздейст-
вием ЭФВ.
Рис. 3.3.
Векторная диаграмма Т-образной схемы замещения ПЭД(А)
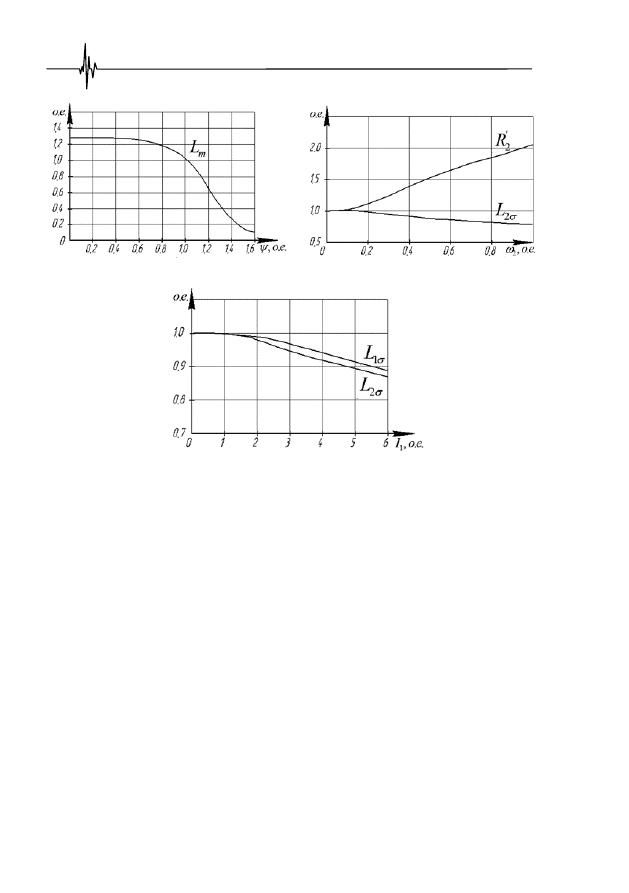
В процедурах формирования ММ и анализа режимов ПЭД(А) часто пре-
небрегают некоторыми параметрами, на первый взгляд мало влияющими
на процесс моделирования и незначительными по численным значениям. Так,
в частности, в такой ситуации в расчетах [24, 27] не учитываются изменения
индуктивности рассеяния
L
1
σ
(
I
1
),
L
2
σ
(
I
1
) от частоты ω
2
тока ротора [28].
Однако анализ зависимостей (рис. 3.4,
а
,
б
) показывает, что изменениями
индуктивности цепи намагничивания
L
m
(Ψ) и сопротивления ротора
R
2
′(ω
2
)
нельзя пренебрегать ввиду возникновения неконтролируемого роста
погрешностей моделирования.
1
2
1
L
2
L
Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
76
а б
в
Рис. 3.4.
Статические зависимости изменения основных параметров ПЭД(А)
Для ПЭД(А), как правило, используют АД с короткозамкнутым рото-
ром. В ММ ПЭД(А) на основе системы уравнений Парка – Горева [29] отра-
жаются процессы насыщения главной цепи намагничивания, изменение
сопротивления ротора в функции скольжения, потери в стали. При этом исполь-
зуются следующие общепринятые допущения:
1.
Считаются симметричными магнитные и электрические цепи ПЭД(А).
2.
Не учитываются потери в стали ротора и влияние гистерезиса
при перемагничивании стали на форму токов и потокосцеплений [30].
Кроме того, необходимо учесть и оценить влияние эффекта насыщения
магнитной системы основным магнитным потоком, явление вытеснения тока
в стержнях ротора, величину потерь в стали устройства. После корректиров-
ки и уточнения параметров схемы замещения ПЭД(А) в ММ необходимо
ввести нелинейные зависимости
m
L
и
2
2
R
[31].
В ММ на основе уравнений Парка – Горева [28] используются обоб-
щенные векторы в системе координат, вращающейся с угловой скоростью
k
для АД с короткозамкнутым ротором.

Глава 3. Математические модели ПЭУ
77
Как было сказано ранее, не нарушая общности рассуждений и допуще-
ний при построении ММ ПЭД(А), можно использовать известные общепри-
нятые положения [28–32]:
1
1
1
1
1
'
2
2
2
2
'*
1
2
;
0
;
;
.
k
k
m
c
d
U
R i
j
d
d
R
i
j
d
M
p L
i i
d
J
M
M
d
(3.1)
'
2
1
2
1
1
1
2
1
2
1
2
'
'
1
2
1
2
1
2
2
2
2
1
2
;
;
;
.
m
m
m
m
m
m
L
L
L
i
L
i
i
L L
L
L
L
L
i
L
i
i
L L
L
(3.2)
Системы (3.1) и (3.2) записаны в координатах
x
–
y
–0, что позволяет
оперировать производными потокосцеплений и соответствующими алгеб-
раическими выражениями:
1
1
2
1
1
2
1
1
2
2
1
2
1
2
1
1
2
1
1
2
1
2
2
1
2
1
2
'
'
2
2
1
1
2
1
2
2
2
1
2
1
2
'
'
2
2
1
2
2
2
1
2
;
;
(
)
;
x
x
m
x
x
k
y
m
m
y
y
m
y
k
x
m
m
x
x
m
x
k
y
m
m
y
y
m
d
R L
R L
U
d
L L
L
L L
L
d
R L
R L
d
L L
L
L L
L
d
R
L
R
L
d
L L
L
L L
L
d
R
L
R
d
L L
L
1
2
2
1
2
1
2
1
2
2
1
2
(
)
;
;
.
m
y
k
x
m
m
y
x
x
y
m
c
L
L L
L
p L
M
L L
L
d
J
M
M
d
(3.3)
Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
78
Из векторной диаграммы следует:
1
2
m
i
i
i
.
(3.4)
Введем обозначения:
−
1
1
m
L
L
L
индуктивность рассеяния статорной обмотки;
−
2
2
m
L
L
L
индуктивность рассеяния роторной обмотки;
− потокосцепления статора и ротора:
1
1
1
2
2
2
m
m
m
m
L
i
L
i
L
i
L
i
. (3.5)
Пользуясь выражением (3.2) в координатных осях
x
–
y
–0, можно запи-
сать зависимости для потокосцеплений и токов:
'
'
1
1
1
2
1
1
1
2
'
'
2
2
2
1
2
2
2
1
2
2
1
1
;
;
;
;
;
x
x
m
x
y
y
m
y
x
m
x
x
y
m
y
y
x
y
L i
L
i
L i
L
i
L
i
L i
L
i
L i
(3.6)
2
1
2
2
1
2
1
.
.
1
2
2
1
2
1
2
1
2
1
'
'
1
2
1
2
2
2
2
1
2
1
2
;
;
;
.
y
m
y
x
m
x
x
п ст
y
m
m
y
m
y
x
m
x
x
y
m
m
L
L
L
L
i
i
i
L L
L
L L
L
L
L
L
L
i
i
L L
L
L L
L
(3.7)
На данном этапе можно определить потери, возникающие в стали ПЭД(А),
по росту активной составляющей тока статора
1
x
i
на величину тока
.
.
п ст
i
(ток
потерь в стали).
Обозначив
2
2
1
1
1
R
x
y
i
i
i
и
'
'2
'2
2
2
2
R
x
y
i
i
i
, можно определить:
– коэффициент мощности ПЭД(А)
1
1
cos
x
R
i
i
;
(3.8)
– действующие значения токов фаз статора и ротора:
I
1
1
3
R
i
I
и
'
'
2
2
3
R
i
I
;
(3.9)

Глава 3. Математические модели ПЭУ
79
– КПД ПЭД(А):
2
'2
'
.
1
1
2
2
ст
R
R
M
M
P
i
R
i
R
.
(3.10)
Для большинства АД [33] справедлива оценка величин потерь в стали
по эмпирическому выражению
P
ст
(
P
2
н
/
н
Р
2
н
)
0,25.
(3.11)
Тогда соответствующий ток
.
.
.
1
/
3
п ст
ст
н
i
P
U
определяется при но-
минальных значениях мощности
Р
2
н
и КПД
н
ПЭД(А).
Практический интерес для дальнейшего исследования представляет опреде-
ление КПД ПЭД (3.10). Для количественной оценки выработки ресурса системы
ПЭУ в составе предлагаемых методик и алгоритмов по повышению эксплуата-
ционной эффективности ПЭУ нефтедобычи введем в выражение (3.10) безраз-
мерный коэффициент
Ϝ
. Данный коэффициент определяет относительную ве-
личину уменьшения внутренних возможностей ПЭУ в целом и отдельно
по рассматриваемым элементам в каждом отдельно взятом процессе ЭФВ.
Иначе для новой установки
Ϝ
= 1 и, соответственно, КПД определяется
номинальными (паспортными) значениями важнейших параметров.
С течением времени эксплуатации под воздействием ЭФВ происходит выра-
ботка ресурса элементов ПЭУ и, соответственно, снижение ее производи-
тельности и заложенных при проектировании запасов стойкости и надеж-
ности, при этом значения коэффициента
Ϝ
также варьируются.
Это позволяет на основе дальнейшего анализа дать корректную оценку
текущего состояния парка ПЭУ, выработать стратегию повышения эксплуа-
тационной эффективности и, как следствие, ограничения повышенного зна-
чения аварийности электрооборудования нефтедобычи:
2
'2
'
.
1
1
2
2
ст
R
R
M
F
M
P
i
R
i
R
.
(3.12)
В сложившихся условиях эксплуатации погружного оборудования неф-
тедобычи, совместной работы элементов современных ПЭУ снижается их
внутренняя стойкость в целом и по составляющим к разнообразным ЭФВ.
При этом происходит совокупная выработка их ресурсов, что в условиях
хронического недофинансирования неизбежно приводит к большому коли-
честву морально и физически устаревшего электрооборудования. Это явля-
ется формальным обоснованием необходимости формирования математиче-
ской модели развития и накопления дефектов (повреждений).

Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
80
3.2. Математическое моделирование износа
и накопления повреждений в ПЭУ
Рассмотрим ММ накопления повреждений в элементах ПЭУ под влия-
нием ЭФВ, для чего введем скалярную функцию времени
D
(
t
), значения
которой определены на временном интервале [0, 1]. Соответственно,
при
0
D
− повреждений нет, а при
1
D
элемент ПЭУ выработал свой
ресурс. Стоит отметить, что сложные явления и процессы, которые связаны
с аккумуляцией, пересечениями и взаимодействиями элементов в процессах
повреждений, невозможно описать лишь одной скалярной функцией, поэто-
му введем понятие и рассмотрим векторные меры, справедливые
в отношении элементов, для которых наиболее целесообразно представление
их физического толкования в виде моделей.
Примем допущение, что приращение функции
D t
на малом проме-
жутке времени зависит лишь от ее значения в его начале и действующих
на этом промежутке ЭФВ. Считая время непрерывным аргументом, запишем
дифференциальное уравнение:
, )
dD
f(D e
dt
, (3.13)
где
,
f D e
– функция меры повреждений
D
и вектора ЭФВ, которая не отри-
цательна при условии, что (3.13) описывает кумулятивный процесс;
е t
– заданная функция времени
.
Граничные условия для уравнения (3.13)
D
(0) = 0;
D
(
T
) =
1 (3.14)
устанавливаются априори: первое − для момента времени
t
= 0, второе −
для момента времени до полного использования ресурса
Т.
Формально вели-
чина
Т
определяется решением обратной задачи для уравнения (3.13).
Отметим, что при анализе повторно-кратковременных режимов работы
электроустановок или при циклическом характере воздействий ЭФВ целесо-
образно в отличие от принятого в (3.13) рассматривать в качестве аргумента
дискретное время [34].
Численные значения изменений нагрузки (минимум, максимум, резкий
наброс нагрузки и т. п.) в произвольном суточном периоде можно объеди-
нить в некотором векторе
e
n
(
n −
номер цикла,
n
= 0 начальное состояние).

Глава 3. Математические модели ПЭУ
81
Введя обозначение
D
n
–
величины меры повреждения после окончания
n
-го цикла, можно переписать уравнение (3.13) в виде
1
1
(
,
)
n
n
n
n
D
D
D
e
, (3.15)
где
n
= 1, 2, … и заданы граничные условия
D
0
= 0,
D
N
= 1;
N
− номер цикла,
на котором полностью исчерпан ресурс.
В приведенном равенстве (3.15) правая часть состоит из (
D
n-
1
,
e
n
)
−
положи-
тельной функции вектора ЭФВ
n
-го цикла и меры повреждений
1
n
D
, соответ-
ствующей окончанию (
n –
1)-го цикла.
Если принять, что числовое значение параметра
n
достаточно велико,
а функции
e
n
и
D
n
медленно изменяются в зависимости от
n
, а также
1
/
n
n
D
D
dD dn
,
(3.16)
тогда равенство (3.15) можно представить сглаженном аппроксимацией виде:
dD
ω(D,e)
dt
. (3.17)
Полученное равенство подобно выражению (3.13), однако аргументом
функции является
n
,
а к естественному времени можно перейти через частоту
dn/dt
[35]. При принятом допущении, что частотные характеристики ЭФВ
принадлежат процессу
e
(
t
),
сглаженные процессы дискретного ЭФВ также
относятся к выражению (3.13).
Для решения конкретных задач, связанных с описанием и накоплением
повреждений в оборудовании ПЭУ, возникает необходимость учитывать
как непрерывные, так и дискретные ЭФВ, имея в виду, что каждое такое
воздействие − нестационарный случайный процесс [36].
Дифференциальное уравнение (3.13) может служить математической
моделью для смешанных ЭФВ при многосторонних свойствах и характери-
стиках его правой части и процесса
e
(
t
)
.
Линейное суммирование повреждений.
Рассмотрим вариант выражения
(3.13), когда его правое слагаемое не зависит от величины
D
. Если известно
значение ЭФВ
e
(
t
),
то правая часть уравнения является функцией времени.
При условии
D
(0) = 0 справедливо равенство
t
0
( )
[
)]
D t
f e(τ d
. (3.18)
Время достижения ПЭУ и его элементами предельного состояния (
T
)
найдем из условия
D
(
T
)=1.

Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
82
Обозначим
Т
b
(
e
) = 1/
f
(
e
), тогда:
T
0
1
[ ( )]
b
dt
T e τ
. (3.19)
При
e
= const очевидно, что
Т
=
T
b
(
e
). Это значит, что величина
Т
b
(
e
) равна
ресурсу при стационарном режиме ЭФВ с заданным значением вектора
e
.
Аналогичный результат для дискретных ЭФВ при условии, что правая
часть равенства (3.15) не зависит от
D
n
– 1
, можно записать в виде
N
b
(
e
)
=
1/ω (
e
).
Для нахождения пикового значения числа
N
при сложном ЭФВ необходимо
просуммировать (3.15) при
n
=
1, 2, …,
N
и условии
D
N
= 1:
1
1
1
N
b
n
n
N (e )
. (3.20)
Зависимости
D
b
(
e
) и
N
b
(
e
) определяются для непрерывных и дискретных
ЭФВ процессов соответственно по результатам испытаний.
Рассмотрим реализацию правила линейного суммирования поврежде-
ний следующими действиями. Запишем одно из решений уравнения (3.15)
с правым слагаемым, независимым от
D
n
– 1
:
n
k 1
n
k
D
D
, (3.21)
где Δ
D
k
= 1 /
N
b
(
e
k
) – неисправность на
k
-м цикле.
Рассмотрим аналитическое решение для непрерывного времени, когда
T
удовлетворяет выражению (3.15). Отметим, что значение
d
τ
/
T
b
[
e
(τ)] соот-
ветствует накоплению повреждения на временном интервале [τ, τ +
d
τ].
Известен ряд вариантов [3, 16, 17, 19] реализации правила линейного
суммирования повреждений, основой которых является использование
методов математической статистики [33–37]. Для них характерны следую-
щие общие положения. Так как ЭФВ имеют различную природу происхож-
дения и разные времена воздействия, то есть имеют смешанную структуру,
необходимо их разделение на независимые классы с целью рассмотрения
влияния каждого из них в отдельности. Характерным моментом при этом
является то, что определение показателей долговечности представляет
неустойчивый процесс и требует значительного объема экспериментальных
и статистических данных об объекте.
Учет нелинейности процесса накопления повреждений.
Одно из самых
главных дискуссионных положений по изучению правила линейного сумми-

Глава 3. Математические модели ПЭУ
83
рования повреждений заключается в том, что согласно названному закону
накопление повреждений в ПЭУ при испытаниях изменяется по линейному
закону. На практике данное утверждение имеет расхождение с результатами
наблюдений различных процессов выработки ресурса ПЭУ [38]. Основные
зависимости (3.19) и (3.20) для оценки общего накопления повреждений
можно получить путем расширения гипотезы об изменении закона распре-
деления величины ресурса с течением времени.
Примем, что величина
D
при проведении испытаний изменяется нели-
нейно и
D
=
D
b
(
t,e
), где
e
= const
.
Введем безразмерную переменную
t / T
b
(
e
)
при неизменном
e
, тогда
D
b
=
g
[
t/T
b
(
e
)]. (3.22)
Для функции
g
(
и
)
справедливы условия
g
(0) = 0,
g
(1) = 1,
g
(
и
) – непрерыв-
ная функция и для всех значений
и
выполняется неравенство -
g'
(
u
)
>
0.
Преобразуем выражение (3.22), выполнив дифференцирование по
t.
Для выражения правой части равенства через
D
b
используем обратную
функцию
- g
-1
(
D
b
), получим:
[
]
b
b
-X
b
dD
g g (D )
dt
T (e)
. (3.23)
Полученное выражение (3.23) справедливо для
e
=
const. Но так как оно
выражает изменение переменной
D
и уровня ЭФВ ПЭУ в определенный
момент времени, то можно утверждать, что оно объективно для любого рас-
сматриваемого случая [39]. В итоге можно записать:
1
b
dD
f (D)
dt
T (e)
, (3.24)
где принято, что
1
1
)
[
( )]
-
f (D
g g
D
. (3.25)
Производя интегрирование выражения (3.24) с начальным условием
D
(0) = 0 и разделяя переменные, получим
t
1
0
0
( )
[ ( )]
b
dD
d
f D
T e
. (3.26)
Теперь, интегрируя правое слагаемое (3.26), можно записать
t
0
( )
[ ( )]
b
dτ
D t
T e
, (3.27)

Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
84
обозначая
D
(
t
) величину меры повреждений, которая находится по правилу
линейного суммирования. В этой ситуации авторы [35, 40] определяют ее
как «меру псевдоповреждения».
Рассмотрим уравнение (3.26), левая часть которого удовлетворяет тож-
деству
-1
1
0
( )
[
( )]
dD
g
D
g g
D
,
где
( )
[ ( )]
D t
g D t
. (3.28)
Полученное уравнение (3.28) является моделью накопления поврежде-
ний, основанной на гипотезе об автомодельности процесса, что предполагает
сохранение его подобия при повторах (см. 3.15, 3.20, 3.21 и далее 3.34, 3.36)
некоторому исходному (принятому за базис) независимо от абсолютных
значений параметров объекта, в котором этот процесс протекает.
В правой части уравнения находится величина, характеризующая меру
повреждения в правиле суммирования повреждений, а для автомодельного
процесса она имеет смысл определенной характеристики процесса ЭФВ
на выбранном интервале времени [41]. Так как
g
(1) = 1, условие для опреде-
ления ресурса
T
совпадает с (3.19).
Анализ показывает, что выражение для определения накопления повре-
ждений имеет аналогичный вид как для правила линейного суммирования
повреждений, так и для гипотезы об автомодельности. Однако стоит под-
черкнуть и главное отличие – автомодельная гипотеза позволяет описывать
как линейный процесс накопления повреждений, так и более сложный
при разнообразных ЭФВ в ПЭУ, и может быть использована не только на этапе
проектирования, но и далее на более поздних этапах жизненного цикла
в процессе эксплуатации ПЭУ [42].
3.3. Законы нелинейного суммирования повреждений в ПЭУ
По факту рассмотренная гипотеза об автомодельности приводит к закону
нелинейного суммирования накопления повреждений. Обратимся к уравнению
(3.13) и рассмотрим случай, когда правую его часть нельзя представить произ-
ведением двух функций, зависящих от
D
и от
e
(
t
). Тогда именно статистика
ЭФВ становится первоопределяющим фактором влияния как на промежуточные
результаты значения меры повреждений [43–45], так и на окончательные соот-
ношения при определении величины ресурса.

Глава 3. Математические модели ПЭУ
85
Рассмотрим вариант, когда
D
b
(
t
) =
[
t/T
b
(
e
)]
γ
. Здесь γ – показатель степе-
ни. Если γ < 1, то процесс накопления повреждений замедляющийся, γ > 1 –
ускоряющийся. В выражении (3.26) получаем
( )
g D
D
, поэтому
g
–1
(
D
) =
D
1/γ
. Используя формулу (3.25), получим
f
1
(
D
) =
1
D
, следова-
тельно, выражение (3.13) примет вид
1
( )
b
dD
D
dt
T e
. (3.29)
Для полученного уравнения введем дополнительное условие – параметр
γ
зависит от уровня нагрузки
e
, тогда получим
[ (e) 1]
(e)
( )
( )
b
dD
e
D
dt
T e
. (3.30)
Проанализируем двухступенчатое ЭФВ. Допустим, что при 0
t
<
t
1
и
t
>
t
1
происходит воздействие ЭФВ со значениями
e
1
и
e
2.
Выполним интег-
рирование выражения (3.30) на первом участке, получим
D
(
t
) = [
t/T
b
(
e
1
)]∙λ(
e
1
);
на втором участке с начальным условием при
t
=
t
1
найдем:
D
(
t
) = {[
t
1
/
T
b
(
e
1
)]
∙
γ(
e
1
)
/
γ(
e
2
)
+ (
t
–
t
1
)/
T
b
(
e
2
)} γ(
e
2
)
(
t
>
t
1
) .
Тогда величина
D
= 1 будет достигнута при
1
2
1
2
1
2
( ) / ( )
1
( )
( )
b
b
t
t
e
e
T e
T e
, (3.31)
где
t
1
=
t
1
,
t
2
=
T
–
t
1
.
Полученная зависимость в (3.31) соответствует уравнению (3.22)
и трансформируется в него при выполнении условия γ(
e
1
) =
γ(
e
2
). Если уровень
ЭФВ влияет на γ, то связь между величинами
v
1
= Δ
t
1
/Т
(
e
1
) и
v
2
= Δ
t
2
/T
b
(
e
), харак-
теризующими выработку ресурса, будет нелинейной [46].
Для нахождения отклонения от правила линейного суммирования сле-
дует определить максимальные значения «меры псевдоповреждения» (3.27)
применительно к двухступенчатому ЭФВ:
1
2
1
2
b
b
Δt
Δt
D(T)
T (e )
T (e )
. (3.32)

Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
86
Если выполнить сравнение выражений, полученных в (3.31) и (3.32), то
логически можно установить, что в зависимости от частного γ(
e
1
) / γ(
e
2
) «мера
псевдоповреждения» при условии Δ
t
1
+ Δ
t
2
=
T
,
D
(
T
)
=
1 находится в диапазоне
0 <
D
(
T
) < 2. (3.33)
Установим нижний предел – он соответствует
γ(
e
1
) / γ(
e
2
)
0, для верхнего
предела γ(
e
1
) / γ(
e
2
)
. Выражение (1.33) показывает, что использование моде-
ли нелинейного суммирования повреждений (1.30) предполагает наличие от-
клонений от результата
D
(
T
)
=
1. Данный факт зависит от слагаемого γ(
e
) в вы-
ражении (3.30), которое связано с уровнем нагрузки
e
[46, 47].
Сделанный вывод возможно легко применить для произвольного числа
ступеней ЭФВ. Для этого обозначим: ступенчатое изменение ЭФВ на эле-
мент ПЭУ –
e
1
,
e
2
, …, момент перехода с одной ступени ЭФВ на другую
t
1
,
t
2
, …, продолжительность каждого ЭФВ Δ
t
1
,
Δ
t
2
,
…, число ступеней
m
.
Для нахождения
D
получаем выражение
1
( e )
k
k
(e )
1
( )
{[ (
)]
/
( )}
k
k
b
k
D t
D t
t
T e
(3.34)
при
t
k –
1
<
t
t
k
;
k
=
1, …,
m
.
Найдем по (3.27) «меру псевдоповреждения» при
t
1
+ … +
t
m
=
T,
D
(
T
)=1, она находится в пределах
0 <
D
(
T
) <
m
. (3.35)
В выражении (3.35) нижний предел будет достигнут при
k
= 1, …,
m
,
ес-
ли соблюдено условие γ(
e
k-
1
)
/
γ(
e
k
)
0; верхний предел достигается при ус-
ловии γ(
e
k-
1
) / γ(
e
k
)
.
Величина
e
характеризует некий скалярный параметр, функция γ(
e
) – по-
стоянная его функция, тогда асимптотическое приближение к экстремумам пре-
дельных условий возможно только при быстром изменении функции и если
e
1
,
…,
e
m
представляет монотонно возрастающую или монотонно убывающую
последовательность [48, 49].
Очевидно, что условия, наложенные на зависимость γ(
e
), не будут
выполнены при большом количестве ступеней ЭФВ. Поэтому для подробно-
го описания и изучения нелинейного суммирования накопления поврежде-
ний необходимо совершенствовать экспериментальную базу путем проведе-
ния экспериментов при возрастающих и убывающих по абсолютной величи-
не ЭФВ [50].

Глава 3. Математические модели ПЭУ
87
3.4. Многостадийная модель процессов накопления
повреждений в ПЭУ
Среди представленных ранее моделей нелинейного суммирования
повреждений ПЭУ необходимо особенно выделить многостадийную модель.
Принципы использования данной модели заключаются в гипотезе о том, что
процесс накопления повреждений состоит из двух и более независимых друг
от друга стадий [51]. На протяжении всего жизненного цикла большинства
элементов ПЭУ можно выделить три стадии накопления износа – приработка,
период нормальной эксплуатации, в течение которого скорость изнашивания
приблизительно постоянна, и стадия интенсивного износа, или дегазацион-
ный период.
Каждая из выделенных стадий существенно зависит от уровня ЭФВ,
в особенности важны значения ЭФВ в момент перехода с одной стадии
на другую [52]. Существенную роль в процессе перехода играют немаловаж-
ные факторы, такие как качество организации эксплуатации ПЭУ, культура
эксплуатации, качество и своевременность проведения ТОиР и т. д.
Эксплуатация ПЭУ сопряжена с воздействием на элементы комплекса
ЭФВ, различных по классификации и природе происхождения. Поэтому
для описанных случаев представляется обоснованным построение многоста-
дийных моделей в сочетании с гипотезой об автомодельности. Данный метод
впервые предложил В.В. Болотин для исследования механических систем
[53]. С теоретической точки зрения данные модели могут быть адаптирова-
ны, использованы для анализа и описания накоплений повреждений в ПЭУ
и его элементах.
Предположим, если ввести безразмерную величину времени по отноше-
нию к каждому циклу ПЭУ, то
D
b
(
t
)
можно представить в виде
b , k - 1
1
1
b , k
b , k - 1
t - T
(e)
( )
(
)
T
(e) - T
(e)
b
k
k
k
k
D t
D
D
D
g
(3.36)
при
T
b,k-
1
(
e
)
< t
T
bk
(
e
), где
k
= 1, …,
m
.
В уравнении (3.36)
D
k –
1
и
D
k
обозначены соответствующие меры повреж-
дений для начала и конца
k
-го цикла (
D
0
= 0;
D
m
= 1);
T
b,k
(
e
) – моменты начала
и окончания
k
-го цикла при условии
e
= const (
T
b,k
=
0);
g
k
(
u
) – функции, кото-
рые описывают закон накопления повреждений для каждого из циклов, при-
чем на них накладываются такие же условия, как на
g
(
и
)
в выражении (3.22).

Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
88
Преобразуем полученное выражение аналогично (3.22) и получим диф-
ференциальное уравнение относительно величины
D
:
1
1
1
1
2
1
2
2
1
1
2
1
1
0
b
b
b
m
m
m
b m
b , m -
m
D f (D) / T (e) (
D
D ),
(D
D )f (D) / [T (e) - T (e)] (D
D
D ),
dD
.......................................................................
dt
(D
D
)f (D) / [T (e) - T
(e)]
(D
1
1
D
)
. (3.37)
Правая часть выражения состоит из функций
f
k
(
D
)=
g’
k
[
g
k
-
1
(φ)], которые
подобны функции
f
1
(
D
) из равенства (3.24). Здесь φ
= (
D
–
D
k
-1
) /
(
D
k
–
D
k
-1
). Выражение, полученное в (3.37), отличается от (3.36) тем, что
является более универсальным и может быть применимо для описания нако-
пления повреждений при любом ЭФВ
e
(
t
)
[54]
.
Для каждой из стадий данное
выражение предполагает решение путем разделения переменных. В итоге
получаем:
k
k-1
T
1
T
1 (
1..... )
[ ( )] -
[ ( )]
b k
b , k -
dτ
k
m
T
e τ
T
e
. (3.38)
Решая последовательность уравнений (3.38), определим значения
T
1
, …,
T
m
.
Логика решения позволяет констатировать, что полный ресурс
T
=
T
m
. Если процесс накопления повреждений состоит из двух стадий, то
величину
T
можно найти решением системы
1
T
1
0
1
[ ( )]
b
dτ
T
e
;
1
T
2
1
T
1
[ ( )] -
[ ( )]
b
b
dτ
T
e
T
e
. (3.39)
Используя выражение (3.39) для двухступенчатого ЭФВ, положим, что
при 0
t <
t
1
происходит воздействие
e
1
= const, при
t
t
1
e
2
=
const.
При этом выражения (3.39) имеют вид:
1
1
1
1
1
1
2
1
b
b
Δt
T - Δt
T (e )
T (e )
;
1
2
2
1
2
1
b
b
T - T
T (e ) - T (e )
;
T
1
=
T
b
1
(
e
1
),
1
1
1
2
1
1
1
2
2
1
2
1
b
b
b
b
Δt - T
T - Δt
T (e ) - T (e )
T (e ) - T (e )
.

Глава 3. Математические модели ПЭУ
89
В состав полученных выражений входит величина
T
1
– продолжительность
1-го цикла и величина полного ресурса
Т
. Если убрать
T
1
,
то получим выражения,
связывающие продолжительность этапов ЭФВ Δ
t
1
и Δ
t
2
=
T
– Δ
t
1
:
1
2
1
2
2
2
1
1
2
2
1
b
b
b
b
T (e )
Δt
Δt
T (e ) T (e )
T (e )
;
t
1
<
T
b
1
(
e
1
);
1
2
1
1
1
2
2
1
2
2
1
2
2
1
1
b
b
b
b
b
b
Δt
T (e )- T (e ) Δt
T (e )
T (e ) - T (e ) T (e )
;
t
1
T
b
1
(
e
1
) . (3.40)
По результатам анализа можно сделать выводы: выражения (3.40) устанав-
ливают «кусочно-линейную» зависимость между безразмерными временами
v
1
=
t
1
/T
b
2
(
e
1
)
и
v
2
=
t
2
/T
b
2
(
e
2
)
,
«мера псевдоповреждения» (3.24) соответст-
вует уравнениям (3.33), при
m
циклов приходим к выражениям (3.35). Как
и в нелинейной модели накопления повреждений (3.30), пиковые значения
D
(
T
) достигаются только при условии выполнения жестких ограничений [54].
Рассмотренные модели накопления повреждений дают адекватные показа-
тели накопления повреждений только при достаточном количестве проведен-
ных экспериментов и зафиксированных при этом значениях ЭФВ. Причем исто-
рия ЭФВ имеет ключевое значение.
В сложившихся условиях эксплуатации ПЭО нефтедобычи в процессе
совместной работы элементов современных ПЭУ снижается их внутренняя
стойкость в целом и по составляющим к разнообразным ЭФВ. При этом
происходит совокупная выработка их ресурсов, что в условиях хронического
недофинансирования приводит к большому количеству морально и физиче-
ски устаревшего электрооборудования [6].
Это является формальным обоснованием актуальности создания ММ как
практического инструмента анализа развития и накопления дефектов (повреж-
дений) ПЭУ в целом от множества ЭФВ, совместно действующих на состав-
ляющие его компоненты. Этим инструментом фактически анализа работоспо-
собности ПЭУ является статистическая модель, фактической базой которой
является обобщенная статистическая информация об аварийности ПЭУ
на определенном интервале эксплуатации с возможностью дифференцирован-
ного разделения этой информации по элементам ПЭУ. Важным условием
при этом является сохранение адекватности сформированной аналитической
ММ при наличии принятых существенных допущений и упрощений.

Повышение эффективности эксплуатации
погружных электроустановок нефтедобычи
90
3.5. Выводы по главе
1.
Для ПЭУ предприятий нефтедобычи проведен анализ и отмечена
характерная большая аварийность, значительная часть которой связана
с воздействиями на них разнообразных эксплуатационных физических воз-
действий, и в том числе от окружающей среды. В связи с этим необходимы
как научное обоснование на базе математического моделирования, так
и практические исследования процессов возникновения и развития повреж-
дений в погружных электроустановках ПЭУ.
2.
Научно обоснованы методы анализа потока повреждений и дефек-
тов для погружного электрооборудования ПЭУ.
3.
Разработаны математические модели для анализа эксплуатационных
ресурсов ПЭУ условиях ЭФВ.
4.
Адекватная аналитическая ММ может быть сформирована только
с существенными допущениями и упрощениями. Поэтому названным прак-
тическим инструментом анализа работоспособности ПЭУ может служить
статистическая модель, фактической базой которой является обобщенная
статистическая информация об аварийности ПЭУ.
Оригинал статьи: Глава третья. Математические модели ПЭУ
3.1. Математические модели режимов работы АД в составе ПЭД ПЭУ
3.2. Математическое моделирование износа и накопления повреждений в ПЭУ
3.3. Законы нелинейного суммирования повреждений в ПЭУ
3.4. Многостадийная модель процессов накопления повреждений в ПЭУ
3.5. Выводы по главе






