Глава пятая. Разработка и исследование математической модели эксплуатационной эффективности ПЭД

Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

117

Глава пятая

РАЗРАБОТКА И ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

ЭКСПЛУАТАЦИОННОЙ ЭФФЕКТИВНОСТИ ПЭД

5.1. Классификация элементов ПЭД

как сложной технической системы

Погружные установки нефтедобычи как сложный технический объект

содержат элементы, различные по составу и физической природе (механиче-
ские,  электрические,  гидравлические  и  т. д.).  При  проектировании  таких
объектов  широко  используется  представление  математических  моделей
в виде структурных схем, состоящих из типовых блоков, которые соединены
между собой направленными линиями связи. Каждый блок реализует опре-
деленную функциональную зависимость выходных переменных от входных
переменных.  Использование  вложенных  структур  (макроблоков)  позволяет
в удобном и наглядном виде описывать сложные модели, содержащие сотни
и даже тысячи элементарных блоков. Структурные схемы удобны и при ре-
шении задач анализа и синтеза систем автоматического управления [68].

На сегодняшний день широкое применение в технической отрасли нашли

двухполюсные структурные схемы [69], применяемые для оценки эксплуатаци-
онной эффективности сложного объекта. Главная особенность их состоит в том,
что при производстве расчетов учитываются только элементы, которые ключе-
вым  образом  влияют  на  работоспособность  всего  объекта  в  целом.  Действую-
щие  методы  оценки  эксплуатационной  эффективности  объекта  (в  том  числе
и ПЭУ,  ПЭД)  являются  своего  рода  обобщенными  или  универсальными,  они
применимы  к  обширному  кругу  объектов  с различными  конструктивными
и физическими свойствами, поэтому для одних объектов их применение оправ-
дано, а для других, более сложных систем, их использование недопустимо, так
как в результаты расчетов будет заложена некая погрешность, величина которой
в каждом конкретном случае непостоянна и может влиять на точность расчетов
[70]. Например, рассматриваемый метод допустим для моделирования простей-
ших электротехнических  устройств, где в основном преобладают электронные
компоненты, однако для моделирования надежности ПЭД как сложного объекта
мало  оправдан,  так  как  не  учитывает  конструктивные  свойства  элементов.
Резюмируя  все  выше  изложенное,  можно  заключить,  что  моделирование
эксплуатационной  эффективности  ПЭД  с использованием  двухполюсных
структурных схем предполагает наличие погрешности, величина которой может
быть значительна.

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

118

Методы, основанные на использовании вероятностно-статистических

характеристик  объекта,  также  не  могут  в  полной  мере  гарантировать  высо-
кую  точность  и  достоверность  полученных  результатов  [71].  Среди  основ-
ных  недостатков  можно  выделить  высокий  уровень  погрешности,  вызван-
ный  низкой  репрезентативностью  статистических  данных.  Именно  поэтому
возникает острая необходимость в создании методов оценки эксплуатацион-
ной эффективности и технического состояния ПЭД с более точными резуль-
татами расчетов, в основу которых положен структурный анализ [72, 73].

Стоит отметить, что исследования по построению структурных схем

элементов системы проводились в работах [72–75], в том числе и в СамГТУ
[51,  54].  В  своем  исследовании  автор  рассматривает  процесс  построения
структурно-функциональных  схем  ПЭД  с  повышенным  напряжением,  в  от-
личие  от  работ,  выполненных  ранее  [51,  54,  76].  На  следующем  этапе  вы-
полнения  работы  на  основании  разработанной  структурно-функциональной
схемы  ПЭД  будут  составлены  математические  модели  узлов  и  обобщенная
математическая  модель  эксплуатационной  эффективности  ПЭД,  в  которых
приняты  в  расчет  не  только  свойства,  заложенные  в  описанных  схемах,
но и текущее состояние ПЭД.

В построении структурных схем ПЭД можно выделить ряд особенно-

стей. Во-первых, построение структурных схем выполняется на основе кон-
струкционных  параметров,  так  как  каждый  элемент  конструкции  строго
выполняет свое назначение и отведенный функционал, заложенный при про-
ектировании  объекта  [62].  В  этом  случае  структурные  схемы  выполняются
в виде замкнутых или разомкнутых неориентированных контуров. В класси-
ческом исполнении они имеют направленную структуру элементов. Во-вторых,
«необходимо  учитывать  исходное  и  взаимное  расположение  деталей  и  узлов
конструкции, определенных геометрическими параметрами» [77]. При их нару-
шении система теряет свою работоспособность либо происходит нарушение, ог-
раничение  функциональных  возможностей  объекта.  В-третьих,  следует  учесть,
что  ПЭД  как  сложная  система  состоит  из  множества  деталей  с различными
физическими, тепловыми, химическими свойствами, соединенных между собой
сварными, болтовыми, опрессовочными, паяльными, резьбовыми и пр. видами
контактного  соединения  [78].  Эксплуатационная  эффективность  всей  системы
напрямую зависит от качества выполняемого сопряжения деталей.

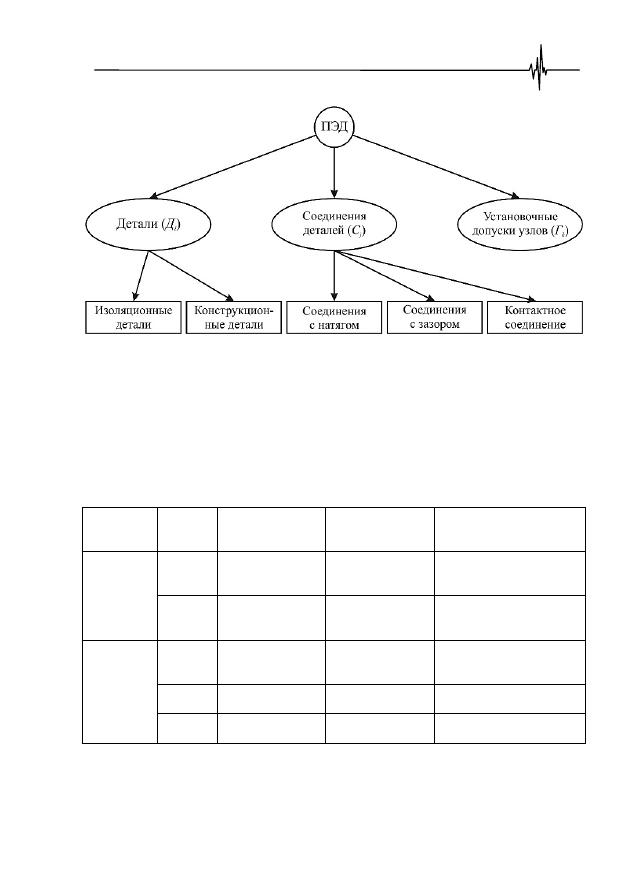
Анализ конструкции ПЭД позволяет выделить три основные группы

элементов – детали, соединения различного вида и установочные геометриче-
ские параметры, учитывающие взаимное соответствие узлов и деталей [79]. Оп-
ределены также подклассы, к которым относятся: изоляционные детали; конст-
рукционные детали; соединения вида натяг или зазор и др. (рис. 5.1).

Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

119

Рис. 5.1.

Классификация элементов погружного электродвигателя

Область факторного пространства, действующего на эти группы эле-

ментов, и его допустимые границы приведены в табл. 5.1. Они дают пред-
ставление о взаимосвязи между факторами и видами отказов.

Таблица 5.1

Классификация элементов ПЭД на основании

конструктивных и физических признаков

Класс

элементов

Обозна-

чение

Подклассы

Основные

факторы

Механизмы отказов

элементов (полные

и частичные)

Детали

Изоляционные
детали

Электротерми-
ческие,
механические

Нарушение электрической
прочности (пробой)
диэлектриков

кi

Конструкционные
детали

Механические

Нарушение
механической прочности
и жесткости

Соединения

Соединения
типа натяг

Механические,
химические

Нарушение
механической прочности
и жесткости

зi

Соединения
типа зазор

Механические
(трение, износ)

Выход параметров
за допустимые пределы

Контактные
соединения

Механические

Отклонение параметров
установки узлов

Произведен анализ причинно-следственной взаимосвязи относительно

механизма отказов в работе погружного оборудования, который послужит осно-
ванием при построении актуальных структурных схем, в основу которых поло-

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

120

жена прежде всего конструктивная база ПЭД [80]. По мере увеличения функ-
циональных назначений элементов будет определена их значимость.

5.2. Формирование математической модели ПЭД

в виде структурно-функциональной схемы

Для построения модели ПЭД на базе конструкции введем некоторую

формализацию с целью дальнейшего облегчения процедуры ее построения.
На основании классификации, приведенной в табл. 5.1, примем условные
обозначения:

– деталь машины;

– соединения;

– установочные гео-

метрические параметры.

Построения структуры можно производить двумя путями: от элемента

к системе или от системы к элементам. Здесь принципиальной разницы нет,
так как результат в обоих случаях должен быть одинаковым. Согласно тер-
минологии теории графов детали, соединения, геометрические установочные
параметры (

) будут вершинами графа, а конструктивные связи обо-

значаются ребрами. Таким образом, мы имеем множество элементов, соеди-
ненных между собой определенным образом.

Если обозначить множество элементов

через

, тогда его

элементы есть

= Σ(

), а система может быть выражена в виде графа

(

) со множеством вершин, представляющих семейство любых воз-

можных пар элементов вида

= (

), указывающих, какие вершины

соединены между собой. Следует отметить важное положение, которое было
указано  ранее:  традиционные  схемы,  как  правило,  являются  двухполюсны-
ми.  Следовательно,  и  ребра  графа  будут  ориентированы.  В данном  случае
они не ориентированы. Тогда выражение для любого ребра будет иметь сле-
дующий  вид:

= (

) = (

). В этом заключается принципиальное

отличие графа, построенного на основании конструктивно-функциональной
базы, от графа, построенного лишь на функциональной базе.

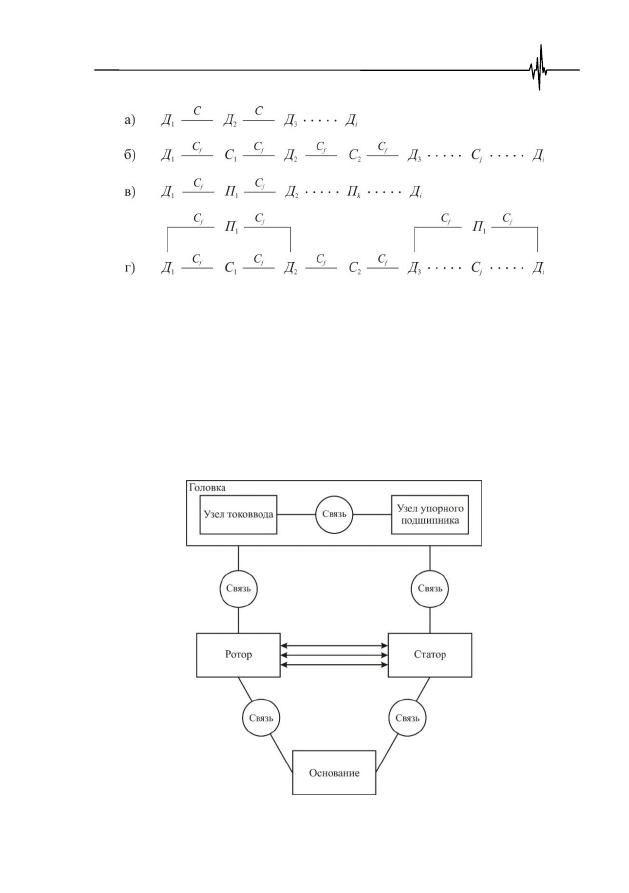
На рис 5.2,

приведена структурная схема соединения элементов

(

;

) в узлы. Между элементами могут быть функциональные связи

и внешние воздействия. На рис. 5.2,

приведена структурная схема для слу-

чая, когда элементы (

;

) соединяются между собой при помощи на-

тяга, зазора, пайки, сварки и др. (

). На рис. 5.2,

приведена структурная схе-

ма, где показана связь между деталями

;

посредством установочного

геометрического параметра. Наиболее общим случаем формирования узла
является использование деталей

, соединений

и установочных геомет-

рических параметров. На рис. 5.2,

в качестве примера приведена структур-

ная схема такого узла.

Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

121

Рис. 5.2.

Варианты исполнения структурных схем электродвигателя:

–

– детали;

–

– соединения;

–

– установочные геометрические параметры;

– функциональные связи

В соответствии с ранее проведенной классификацией и с учетом конст-

руктивных  взаимосвязей  разработана  структурно-функциональная  схема
ПЭД.  На  рис. 5.3  приведена  блок-схема  ПЭД  на  базе  основных  подсистем:
узла  токоввода,  узла  упорного  подшипника,  статора,  ротора,  узла  нижнего
основания.  Приведены  основные  внутренние  связи  между  подсистемами:
механические, магнитные, вентиляционные, а также различные виды соеди-
нений, существующие между ними.

Рис. 5.3.

Структурно-функциональная схема ПЭД

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

122

Такое представление позволяет производить дальнейшее структурно-

функциональное дробление подсистем на элементы.

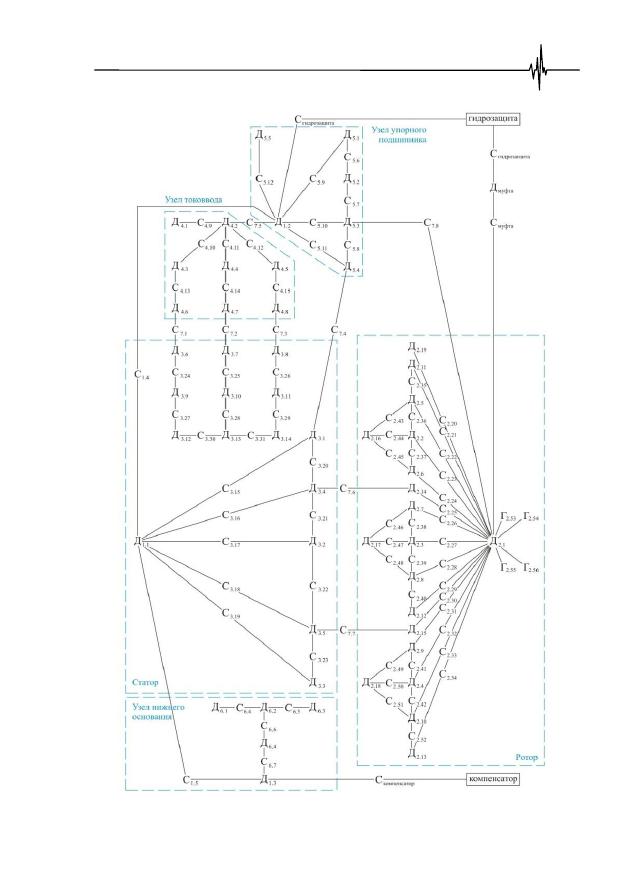
На рис. 5.4 приведена структурно-функциональная схема погружного

электродвигателя,

позволяющая

учесть

детали,

конструктивные

и функциональные связи между ними и другими подсистемами.

Описание принятых обозначений:

1.1

– корпус ПЭД;

1.2

– верхнее

основание корпуса ПЭД;

1.3

– нижнее основание корпуса ПЭД;

2.1

– вал

ротора;

2.2

–

2.4

– пакеты ротора;

2.5

–

2.10

– стопорные кольца;

2.11

–

2.13

–

упорные кольца;

2.14

–

2.15

– подшипники скольжения;

2.16

–

2.18

– «бели-

чья клетка»;

2.15

– турбинка;

3.1

–

3.3

– пакеты статорного железа;

3.4

–

3.5

– немагнитный материал статорного железа;

3.6

–

3.8

– верхние

лобовые части обмоток фаз А, В, С;

3.9

–

3.11

– пазовые части обмоток фаз;

3.12

–

3.14

– нижние лобовые части обмоток фаз;

4.1

– крышка узла токоввода;

4.2

– колодка;

4.3

–

4.5

– гильзы;

4.6

–

4.8

– кабель;

5.1

– крышка;

5.2

– пята;

5.3

– подпятник;

5.4

– резина;

5.5

– обратный клапан;

6.1

– пробка;

6.2

– пере-

пускной клапан;

6.3

– обратный клапан;

6.4

– фильтр;

– муфта.

В построенной структурно-функциональной схеме ПЭД приняты

во внимание параметры соединений между узлами конструкции, поскольку
от качества и состояния выполненных контактных соединений напрямую зави-
сит величина надежности всей установки в целом. Также приняты во внимание
параметры, учитывающие геометрические связи, которые существенно влияют
на надежность ПЭД.

На основании всего вышеизложенного выполнено построение матема-

тической модели вероятности возникновения отказа для каждого из узлов
ПЭД [80, 81]:

1. Математическая модель вероятности возникновения отказа для узла

упорного подшипника. Составим аналитическое выражение вероятности
возникновения отказа для контуров:

а) контур

5.1

5.6

5.2

5.7

5.3

5.8

5.4

А Д



1
5

5.1

5.6

5.1

5.6

5.2

5.1

5.6

5.2

5.7

5.1

5.6

5.2

5.7

5.3

5.1

5.6

5.2

5.7

5.3

5.8

5.1

5.6

5.2

5.7

5.3

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1



 





 



 





 





 



5.8

5.4

) (1

)



Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

123

Рис. 5.4.

Структурно-функциональная схема погружного электродвигателя

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

124

б) контур

1.2

5.9

5.1



1
5

1.2

5.9

1.2

5.9

5.1

( )

)

) (1

)



 



в) контур

1.2

5.10

5.3



1
5

1.2

5.10

1.2

5.10

5.3

( )

)

) (1

)



 



г) контур

1.2

5.11

5.4



1
5

1.2

5.11

1.2

5.11

5.4

( )

)

) (1

)



 



д) контур

1.2

5.12

5.5



1
5

1.2

5.12

1.2

5.12

5.5

( )

)

) (1

)



 



Тогда уравнение звена упорного подшипника будет иметь вид:





Математическая модель вероятности возникновения отказа для узла

упорного подшипника определяется выражением

( )

)

) (1

)

) (1

)

) (1

)

Q Т

Q Q





 



 





 

 



(5.1)

2. Математическая модель вероятности возникновения отказа для узла

токоввода и обмотки статора электродвигателя. Составим аналитическое
выражение вероятности возникновения отказа для контуров:

а) контур

1
4

4.2

4.10

4.3

4.13

4.6

7.1

3.6

3.24

3.9

3.27

3.12



1
4

4.2

4.10

4.2

4.10

4.3

4.2

4.10

4.3

4.13

4.2

4.10

4.3

4.13

4.6

4.2

4.10

4.3

4.13

4.6

7.1

4.2

4.10

4.3

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1



 



 





 



 





 

 



4.6

7.1

3.6

4.2

4.10

4.3

4.13

4.6

7.1

3.6

3.24

4.2

4.10

4.3

4.13

4.6

7.1

3.6

3.24

3.9

4.2

4.10

4.3

4.13

) (1

)

) (1

)

) (1

)

) (1





 





 





 



4.6

7.1

3.6

3.24

3.9

3.27

4.2

4.10

4.3

4.13

4.6

7.1

3.6

3.24

3.9

3.27

3.12

) (1

)

) (1

)

) (1

)





 

 





 



Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

125

б) контур

1
4

4.2

4.11

4.4

4.14

4.7

7.2

3.7

3.25

3.10

3.28

3.13



1
4

4.2

4.11

4.2

4.11

4.4

4.2

4.11

4.4

4.14

4.2

4.11

4.4

4.14

4.7

4.2

4.11

4.4

4.14

4.7

7.2

4.2

4.11

4.4

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1

Q T



 



 





 



 





 

 



4.7

7.2

3.7

4.2

4.11

4.4

4.14

4.7

7.2

3.7

3.25

4.2

4.11

4.4

4.14

4.7

7.2

3.7

3.25

3.10

4.2

4.11

4.4

4.14

) (1

)

) (1

)

) (1

)

) (1

) (







 





 





 



4.7

7.2

3.7

3,25

3.10

3.28

4.2

4.11

4.4

4.14

4.7

7.2

3.7

3.25

3.10

3.28

3.13

) (1

)

) (1

)

) (1

)





 

 





 



в) контур

1
4

4.2

4.12

4.5

4.15

4.8

7.3

3.8

3.26

3.11

3.29

3.14



1
4

4.2

4.12

4.2

4.12

4.5

4.2

4.12

4.5

4.15

4.2

4.12

4.5

4.15

4.8

4.2

4.12

4.5

4.15

4.8

7.3

4.2

4.12

4.5

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1

Q T



 



 





 



 





 

 



4.8

7.3

3.8

4.2

4.12

4.5

4.15

4.8

7.3

3.8

3.26

4.2

4.12

4.5

4.15

4.8

7.3

3.8

3.26

3.11

4.2

4.12

4.5

4.15

) (1

)

) (1

)

) (1

)

) (1





 





 





 



4.8

7.3

3.8

3,26

3.11

3.29

4.2

4.12

4.5

4.15

4.8

7.3

3.8

3.26

3.11

3.29

3.14

) (1

)

) (1

)

) (1

)





 

 





 



г) контур

1
4

3.12

3.30

3.13

3.31

3.14



1
4

3.12

3.30

3.12

3.30

3.13

3.12

3.30

3.13

3..31

3.12

3.30

3.13

3..31

3.14

( )

)

) (1

)

) (1

)

) (1

)



 



 





 

 



контур

1
4

4.1

4.9

4.2



1
4

4.1

4.9

4.1

4.9

4.2

( )

)

) (1

)



 



Тогда уравнение звена токоввода и обмотки статора будет иметь вид





Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

126

Математическая модель вероятности возникновения отказа для узла

токоввода и обмотки статора определяется выражением

( )

)

) (1

)

) (1

)

) (1

)

Q Т





 



 





 

 



(5.2)

3. Математическая модель вероятности возникновения отказа для узла

ротора электродвигателя. Составим аналитическое выражение вероятности
возникновения отказа для контуров:

а) контур

1
2

2.11

2.35

2.5

2.36

2.2

2.37

2.6



1
2

2.11

2.35

2.11

2.35

2.5

2.11

2.35

2.5

2.36

2.11

2.35

2.5

2.36

2.2

2.11

2.35

2.5

2.36

2.2

2.37

2.11

2.35

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1



 



 





 

 



 



 



 



2.36

2.2

2.37

2.6

)

) (1

)



 



б) контур

1
2

2.16

2.43

2.5



1
2

2.16

2.43

2.16

2.43

2.5

( )

)

) (1

)



 



в) контур

1
2

2.16

2.44

2.2



1
2

2.16

2.44

2.16

2.44

2.2

( )

)

) (1

)



 



г) контур

1
2

2.16

2.45

2.6



1
2

2.16

2.45

2.16

2.45

2.6

( )

)

) (1

)



 



д) контур

1
2

2.7

2.38

2.3

2.39

2.8

2.40

2.12



1
2

2.7

2.38

2.7

2.38

2.3

2.7

2.38

2.3

2.39

2.7

2.38

2.3

2.39

2.8

2.7

2.38

2.3

2.39

2.8

2.40

2.7

2.38

2.3

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1



 



 





 

 





 



 





 



2.39

2.8

2.40

2.12

) (1

)



е) контур

2.17

2.46

2.7



2.17

2.46

2.17

2.46

2.7

( )

)

) (1

)



 



ж) контур

1
2

2.17

2.47

2.3



1
2

2.17

2.47

2.17

2.47

2.3

( )

)

) (1

)



 



Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

127

з) контур

1
2

2.17

2.48

2.8



1
2

2.17

2.48

2.17

2.48

2.8

( )

)

) (1

)



 



и) контур

1
2

2.9

2.41

2.4

2.42

2.10

2.52

2.13



1
2

2.9

2.41

2.9

2.41

2.4

2.9

2.41

2.4

2.42

2.9

2.41

2.4

2.42

2.10

2.9

2.41

2.4

2.42

2.10

2.52

2.9

2.41

2.4

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1

)

Q T



 



 





 

 



 



 



 





2.42

2.10

2.52

2.13

) (1

)



к) контур

1
2

2.18

2.49

2.9



1
2

2.18

2.49

2.18

2.49

2.9

( )

)

) (1

)



 



л) контур

1
2

2.18

2.50

2.4



1
2

2.18

2.50

2.18

2.50

2.4

( )

)

) (1

)



 



м) контур

2.18

2.51

2.10



2.18

2.51

2.18

2.51

2.10

( )

)

) (1

)



 



н) контур

1
2

2.1

2.20

2.19



1
2

2.1

2.20

2.1

2.20

2.19

( )

)

) (1

)



 



о) контур

1
2

2.1

2.21

2.11



1
2

2.1

2.21

2.1

2.21

2.11

( )

)

) (1

)



 



п) контур

1
2

2.1

2.22

2.5



1
2

2.1

2.22

2.1

2.22

2.5

( )

)

) (1

)



 



р) контур

2.1

2.23

2.2



2.1

2.23

2.1

2.23

2.2

( )

)

) (1

)



 



с) контур

1
2

2.1

2.24

2.6



1
2

2.1

2.24

2.1

2.24

2.6

( )

)

) (1

)



 



т) контур

1
2

2.1

2.25

2.14



1
2

2.1

2.25

2.1

2.25

2.14

( )

)

) (1

)



 



у) контур

1
2

2.1

2.26

2.7



1
2

2.1

2.26

2.1

2.26

2.7

( )

)

) (1

)



 



Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

128

ф) контур

2.1

2.27

2.3



2.1

2.27

2.1

2.27

2.3

( )

)

) (1

)



 



х) контур

1
2

2.1

2.28

2.8



1
2

2.1

2.28

2.1

2.28

2.8

( )

)

) (1

)



 



ц) контур

2.1

2.29

2.12



2.1

2.29

2.1

2.29

2.12

( )

)

) (1

)



 



ч) контур

2.1

2.30

2.15



2.1

2.30

2.1

2.30

2.15

( )

)

) (1

)



 



ш) контур

1
2

2.1

2.31

2.9



1
2

2.1

2.31

2.1

2.31

2.9

( )

)

) (1

)



 



щ) контур

2.1

2.32

2.4



2.1

2.32

2.1

2.32

2.4

( )

)

) (1

)



 



ы) контур

1
2

2.1

2.33

2.10



1
2

2.1

2.33

2.1

2.33

2.10

( )

)

) (1

)



 



э) контур

1
2

2.1

2.34

2.13





1
2

2.1

2.34

2.1

2.34

2.13

( )

)

) (1

)





 



ю) контур

2.1

2.52





1
2

2.1

2.52

( )

)





 

я) контур

1
2

2.1

2.53





1
2

2.1

2.53

( )

)





 

аа) контур

2.1

2.54





1
2

2.1

2.54

( )

)





 

бб) контур

1
2

2.1

2.55





1
2

2.1

2.55

( )

)





 

Тогда уравнение звена ротора будет иметь вид:



 









 



 



 



Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

129

Математическая модель вероятности возникновения отказа для узла

ротора ПЭД определяется выражением

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

Q T





 



 





 

  





 





 

) (1

)

) (1

)















 



(5.3)

4. Математическая модель вероятности возникновения отказа для узла

магнитопровода статора электродвигателя. Составим аналитическое выра-
жение вероятности возникновения отказа для контуров:

а) контур

3.1

3.20

3.4

3.21

3.2

3.22

3.5

3.23

3.3



1
3

3.1

3.20

3.1

3.20

3.4

3.1

3.20

3.4

3.21

3.1

3.20

3.4

3.21

3.2

3.1

3.20

3.4

3.21

3.2

3.22

3.1

3.20

3.4

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1



 



 





 

 



 





 



 



3.21

3.2

3.22

3.5

3.1

3.20

3.4

3.21

3.2

3.22

3.5

3.23

3.1

3.20

3.4

3.21

3.2

3.22

3.5

3.23

3.3

)

) (1

)

) (1

)

) (1

)

) (1

)

) (1

)



 



 





 



 





 



б) контур

1.1

3.15

3.1



1
3

1.1

3.15

1.1

3.15

3.1

( )

)

) (1

)



 



в) контур

1.1

3.16

3.4



1
3

1.1

3.16

1.1

3.16

3.4

( )

)

) (1

)



 



г) контур

1.1

3.17

3.2



1
3

1.1

3.17

1.1

3.17

3.2

( )

)

) (1

)



 



д) контур

1.1

3.18

3.5



1
3

1.1

3.18

1.1

3.18

3.5

( )

)

) (1

)



 



е) контур

1.1

3.19

3.3



1.1

3.19

1.1

3.19

3.3

( )

)

) (1

)



 



Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

130

Тогда уравнение звена магнитопровода статора будет иметь вид:







Математическая модель вероятности возникновения отказа для узла

магнитопровода статора ПЭД определяется выражением:

( )

)

) (1

)

) (1

)

) (1

)

) (1

)

Q Т





 



 





 

 





 



(5.4)

5. Математическая модель вероятности возникновения отказа для узла

нижнего основания ПЭД. Составим аналитическое выражение вероятности
возникновения отказа для контуров:

а) контур

1.3

6.7

6.4

6.6

6.2

А Д



1
6

1.3

6.7

1.3

6.7

6.4

1.3

6.7

6.4

6.6

1.3

6.7

6.4

6.6

6.2

( )

)

) (1

)

) (1

)

) (1

)



 





 



 



б) контур

6.1

6.4

6.2



1
6

6.1

6.4

6.1

6.4

6.2

( )

)

) (1

)



 



в) контур

6.2

6.5

6.3



1
6

6.2

6.5

6.2

6.5

6.3

( )

)

) (1

)



 



Тогда уравнение звена нижнего основания будет иметь вид:





Математическая модель вероятности возникновения отказа для узла

нижнего основания ПЭД определяется выражением:

 

)

) (1

)





 



(5.5)

Для получения вероятности безотказной работы ПЭД в функции

от времени,  выраженной  в  количественном  эквиваленте,  необходимо
в полученные  математические  модели  вероятности  возникновения  отказа
для  рассмотренных  узлов  (5.1)–(5.5)  подставить  рассчитанные  вероятности
возникновения  отказа  для  узлов  ПЭД  [102].  Составленная  математическая
модель позволяет оценить вероятность возникновения отказа в работе  ПЭД

Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

131

с учетом его структурных и функциональных связей, а также конструкцион-
ных особенностей.

В результате комплекса преобразований математических моделей узлов

ПЭД получено выражение для вероятности возникновения отказа погружно-
го электродвигателя в общей форме:

 





( )

i j

Q E

К Q E T

E T



















 



























, (5.6)

где слагаемое

( )

Q E T









представляет собой вероятность возникновения

отказа для

-го узла;

– коэффициент, определяемый по кривым оценки ос-

таточного ресурса ПЭД, разработанным и составленным в главе 4. Они от-
ражают зависимость остаточного ресурса ПЭД от времени эксплуатации.

Предложенная методика [82–85] дает возможность производить оценку

эксплуатационной эффективности как ПЭД, так и элементов его конструк-
ции с учетом их остаточного ресурса в процессе эксплуатации. Кроме того,
данная методика позволяет оценивать эксплуатационную эффективность как
всей системы ПЭУ, так и отдельных ее звеньев, что в корне меняет сущест-
вующие подходы и делает возможным обнаружить «слабые» элементы кон-
струкции ПЭУ и внести соответствующие коррективы на всех этапах жиз-
ненного цикла системы.

Для сложных технических систем (к которым относятся ПЭУ и, в част-

ности, ПЭД) по технологическому процессу, имеющих неоднократные преобра-
зования  энергии,  анализ  показателей  [86],  характеризующих  функциональные
свойства  системы  по  ряду  ключевых  признаков  (конструктивному,  электриче-
скому,  магнитному  и  т. п.),  является  необходимым  и  существенно  влияет
на величину погрешности, сводя ее значение к минимуму [54, 87].

5.3. Оценка параметров постулируемых законов распределения

постепенных отказов деталей в процессе эксплуатации

В результате интеллектуального анализа и обработки статистических

гипотез [88] установлено, что функция плотности распределения наработок
на отказ конструктивных элементов ПЭУ подчиняется нормальному закону
распределения





;

N t m D

. Установлено, что рассматриваемые гипотезы

не могут  быть  использованы  в  качестве  универсальных  для  всех  элементов
системы,  так  как  в  ряде  случаев  дают  неадекватные  оценки  эмпирических
функций  в  результате  значительной  величины  погрешности  (в некоторых

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

132

случаях ≥ 20 %), возникающей от воздействия  непрогнозируемых и  нерегу-
лируемых факторов, и существенно влияют на результат оценки эксплуата-
ционной эффективности [107, 108]. В процессе исследования вероятностно-
статистических характеристик функций распределений вероятности на отказ
конструктивных  элементов  ПЭД  установлено,  что  отказы,  возникающие
в результате износа узлов и деталей, могут быть описаны с помощью асим-
метричного распределения. В этом случае необходимо использовать усечен-
но-нормальную  функцию  распределения





; ;

;

N t с m D

, позволяющую све-

сти  к минимуму величину  погрешности (ошибки)  и,  как следствие,  обосно-
ванно  использовать  описанные  модели  [59].  Описание  использования  усе-
ченно-нормальной  функции  распределения  по  известным  значениям  пара-
метров матожидания и дисперсии заключается в следующем.

Плотность распределения вероятности на отказ находится по выражению:

(5.7)

В данном выражении слагаемое

определяет нормальное распределение с параметром 0,1.

Функция распределения вероятности на отказ определяется:

(5.8)

Для дальнейших расчетов необходимо составить систему из уравнений:

(5.9)

где слагаемые системы уравнений обозначены как:

– произвольная

величина, определяющая длительность до рассматриваемого отказа;

– среднее расстояние до 1-го отказа;

– дисперсия для 1-го отказа;

– элемент

-й подсистемы;

– соответствующее среднее усеченно-

 



































exp

 











 























 











































Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

133

нормального распределения;

– дисперсия для усеченно-нор-

мального распределения.

Решением системы уравнений служит величина вероятности возникно-

вения отказа элемента при известных уровнях отказа

, определяемая по

выражению:

(5.10)

в котором

, σ – решения уравнений в зависимости от

Согласно [60] установлено, что для нахождения решения системы нели-

нейных уравнений целесообразно использовать итерационный метод Нью-
тона. Коротко рассмотрим общую процедуру этого метода. Далее парамет-
рам



соответствуют обозначения

x, y.

На следующем этапе расчета

составим систему уравнений

Рассмотрим матрицу Якоби:

с помощью которой возможно построение итерационной процедуры в виде:































 











































































Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

134

в которой

– детерминант матрицы

Представим величину текущих координат:

;

Для величины первоначального состояния (другими словами, нулевого

приближения)

x y

можно установить значение искомого корня [108].

Выражение для основных моментов будет являться зависимостью:

Если обозначить

, то можно записать:

(5.11)























 

    



















 

    



































































exp























































































































































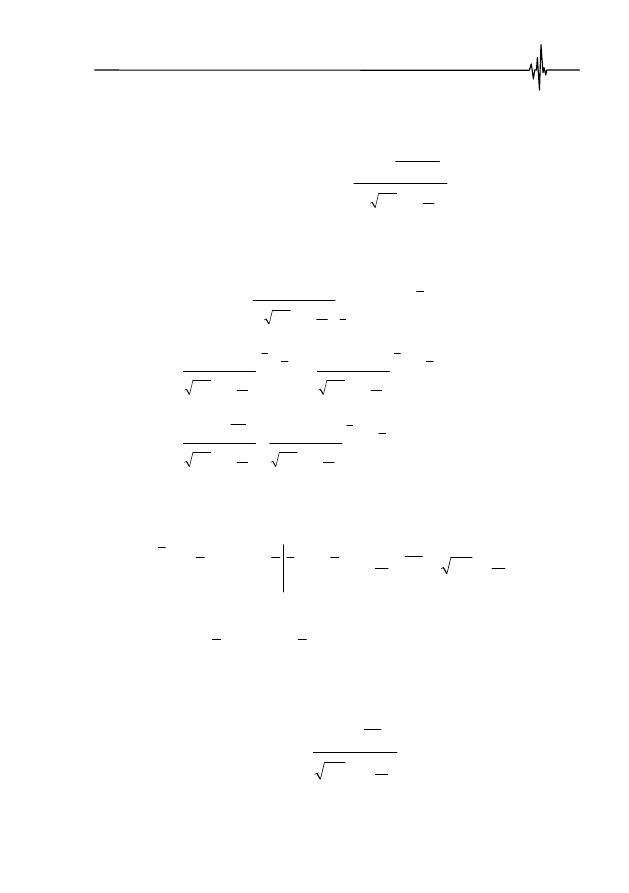
Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

135

Далее вычислим значение 2-го момента:

(5.12)

С учетом обозначений, принятых ранее, имеем:

(5.13)

Найдем значение интеграла:

Решением интеграла служит выражение:

(5.14)





 

















































exp





























































































































































































Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

136

На основании полученного выражения (5.14) составим систему уравне-

ний, решив которые, получим значения параметров усеченно-нормального
распределения:

(5.15)

Введем обозначения:

(5.16)

Для решения полученных уравнений в (5.16) необходимо найти значе-

ния четырех частных производных

Составим выражение для вычисления 1-й частной производной:

(5.17)



















































































































































































































































;

Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

137

Составим выражение для вычисления 2-й частной производной:

(5.18)

Составим выражение для вычисления 3-й частной производной:

(5.19)

Составим выражение для вычисления 4-й частной производной:

(5.20)











































































































































































































































































































































Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

138

Далее, подставив рассчитанные значения производных

в матрицу и используя итерационный процесс модифицированного метода
Ньютона [89], можно выполнить соответствующий расчет усеченно-
нормального распределения.

Результатом проведенного интеллектуального исследования, математи-

ческих вычислений и анализа полученных результатов послужило составле-
ние  композиционной модели оценки эксплуатационной эффективности эле-
ментов  конструкции  ПЭУ  и,  в  частности,  ПЭД.  Она  позволит  вносить  кор-
рективы в существующие гипотезы и достигать адекватных оценок парамет-
ров надежности в процессе эксплуатации оборудования  ПЭУ и, как следст-
вие, модифицировать существующие параметры и подходы ТОиР.

5.4. Определение уточненных уровней

эксплуатационной эффективности элементов ПЭД

при различных законах распределения отказов

Экспоненциальное распределение (показательное распределение) экс-

плуатационной эффективности внезапных отказов элементов ПЭД.

Конструкционные  детали  и  узлы  ПЭД  подвержены  влиянию  разнородных
внешних  и  внутренних  факторов.  Поэтому  их  ресурс  в  значительной  мере
зависит от интенсивности воздействия на них ЭФВ, этим и объясняется от-
личие  элементов  друг  от  друга  в  наработке  до  восстановления  (замены)
и количестве  отказов  за  рассматриваемый  промежуток  времени  [90].  Оче-
видно, что детали ПЭД с наибольшим ресурсом и наименьшим количеством
отказов будут зависеть от закона распределения [91]. Если принять, что ус-
тановлен  закон  распределения  отказов  с  параметрами





; ;

N t T



, известна

наработка на очередной ремонт или ТО для элемента, то можно определить
вероятность наработки детали выше установленного значения:

(5.21)

где

– наработка;

(

) – функция плотности.

Происходит уменьшение количества отказов в диапазоне 0

-t

при боль-

ших значениях вероятности отказа

(

). Для определенных значений поток

отказов в диапазоне 0

-t

соответствует условиям пуассоновского потока [82]

и является стационарным. Для составления модели вероятности отказа ПЭД
в диапазоне 0

-t

следует в зависимость

(

) подставить выражение, получен-

ное в (5.21).







 













Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

139

Выполнив интегрирование обеих частей уравнения, получим зависимость:









 

 



 





(5.22)

При анализе полученной зависимости становится очевидно, что

в данном  выражении  не  учитывается  численный  состав  элементов  установ-
ки.  Поэтому  необходимо  использовать  методику,  в  которой  исследуется
вероятность  наработки  детали  выше  установленного  значения,  с исполь-
зованием в расчетах значения количества эксплуатируемых элементов системы,
удовлетворяющих  тому  требованию,  что  жизненный  цикл  установки  имеет
конечное (предельное) значение [78, 92].

Для данной методики примем, что за время

ср

произошло

отказов

для

одинаковых элементов системы, находящихся в работе. Тогда можно

записать выражение:

(5.23)

В полученном равенстве слагаемое

получено эмпирическим путем.

Произведя логарифмирование, получаем:

(5.24)

Из выражения (5.24) можно выразить величину интенсивности отказов:

(5.25)

Подставив выражение (5.25) в равенство (5.22), получим:

(5.26)

Если за текущее время

произошло

отказов для

одинаковых эле-

ментов системы, находящихся в работе, то можно записать выражение:

(5.27)

ср







ср































 



ср





































ср

exp

























 





ср

exp

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

140

Преобразовав выражение (5.27), получим:

(5.28)

Получена модель, в которой полно отражен процесс возникновения

отказа элемента и конструктивно учитывается взаимосвязь количества отказов
с надежностью и количеством находящихся в работе одинаковых элементов.

Нормальное распределение постепенных отказов элементов ПЭД.

Рас-

смотрим  основные  условия  формирования  параметрических  отказов.
Под воздействием  температурно-силовых  факторов  и  внешних  факторов
могут  появляться  и  развиваться  во  времени  процессы  деформации,  износа,
разрушения элементов технической системы, которые  приводят к ее  повре-
ждению. Параметрический отказ возникает в том случае, если повреждения
приведут к изменениям какого-либо выходного параметра, а значение этого
параметра выйдет за установленные пределы [86]. Таким образом, парамет-
рический  закон  распределения  применяется  для  описания  износа  деталей,
узлов  и  их  соединений,  а  изменение  его  параметров  описывается  Гауссов-
ским  случайным  процессом  [84],  то  есть  представляет  собой  контролируе-
мый  случайный  процесс

(

) с параметрами СКО

(

) и матожиданием

(

Для описываемого процесса

(

) установим двухсторонние границы, выход

из которых приведет к релаксационному отказу. То есть выход из интервала





A B A





приведет к отказу элемента системы. Примем

допущение, что СКО и среднее значение величины меняются во времени
линейно до времени

ср

, то есть

 

;

d t





, где

const

 





ср



. Тогда можно записать равенство:

(5.29)

При условии, что

, для

элементов

 

ср

S Т



, а для

элементов

 

ср

S Т



. Тогда получим систему уравнений:

(5.30)







































 





ср

exp

  







 











 













 









 





ср



dТ

ср















 

















 















 



Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

141

где слагаемые

выражают значения оценок, полученных из опытных

данных.

Далее, используя метод последовательных приближений, необходимо

вычислить

из выражения (5.30).

Преобразуя одно из уравнений системы (5.30), получим:

(5.31)

В результате дальнейших преобразований:

(5.32)

здесь

 



– функция, обратная табулированной функции Лапласа

 

ф t

Выполнив преобразование (5.30) и (5.31), получаем:

(5.33)

В явном виде уравнение примет вид:

(5.34)

Преобразуем уравнение, полученное в (5.34):

(5.35)

В результате получаем систему уравнений:

(5.36)

ср

















 































 



ср















 



ср



ср



















 

































 



ср

































 





























 



ср



Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

142

Из полученной системы уравнений можно определить СКО

и матожидание путем их совместного решения. Если выполнить деление
левой и правой части 1-го уравнения на 2-е, то получим равенство вида:

(5.37)

После видоизменения получившегося в (5.37) равенства новое равенст-

во примет вид:

(5.38)

В явном виде уравнение примет вид:

(5.39)

В результате получаем выражение для нахождения матожидания износа

деталей ПЭД:

(5.40)

На основе произведенных математических вычислений выведем формулу

для нахождения СКО деталей:

(5.41)



































ср









































ср































































dТ

ср













































































ср

















































































Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

143

Соответственно, выражение для текущего времени

примет вид:

(5.42)

здесь приняты обозначения:

– количество элементов, для которых зазор

уменьшился



за время

;

– количество элементов, для которых зазор

уменьшился



за время

На основе произведенных математических вычислений получаем урав-

нение, которое связывает количество отказов с параметрами распределения:

. (5.43)

Выражение для текущего времени

примет вид:

(5.44)

По факту выполненных преобразований получаем окончательное выра-

жение для нахождения общего количества отказов:

. (5.45)

В результате произведенных математических преобразований выведена

математическая модель, которая отражает численную взаимосвязь между
величиной релаксационных отказов деталей и износом ПЭД, определяемых
с использованием табулированных функций Лапласа [85, 86].

Усеченное нормальное распределение отказов элементов ПЭД.

Ввиду

влияния разнообразных функциональных воздействий на элементы конст-
рукции и некоторые детали ПЭД [87] закон их износа

описывается усе-

ченно-нормальным распределением, которое имеет вид [78]:

















ср















 

















 











































 















 





ср





















 













 







 





 





 





 





 





 





 





 







































































































Аф

ср















Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

144

здесь функция под интегралом описывается выражением:

(5.46)

На основание поставленной задачи исследования и особенностей эле-

ментов системы [78] считаем, что при условии

 

S t



отказ наступит

за время

. Так же следует найти значения параметров

и σ.

Для рассматриваемого распределения за время

ср

произошло

отка-

зов из общего количества

элементов. Тогда для

элементов получим

 

ср

S T



, где

A B



– некоторое число, которое подбирается. Тогда мож-

но записать:

(5.47)

В системе уравнений (5.47) выполним замену слагаемых в функции

под интегралом на выражение:

(5.48)

В интегралах системы уравнений (5.47) запишем:

В результате проведенных преобразований можно записать:

. (5.49)





















































exp

если















;

ср









ср

dТ





dТ

ср



























dТ

ср



























 











































 



Глава 5. Разработка и исследование математической модели

эксплуатационной эффективности ПЭД

145

Составлены математические модели, позволяющие произвести оценку

параметров различных законов распределения отказов элементов ПЭД
и представить в численном виде характеристики внезапных и релаксацион-
ных отказов.

5.5. Выводы по главе

Предложена методика оценки эффективности эксплуатации сложных

систем  на  примере  ПЭД,  основанная  на  использовании  структурно-
функциональных  схем,  позволяющая  оценивать  эксплуатационную  эффек-
тивность  как  всей  системы,  так  и  отдельных  ее  звеньев.  В  данном  подходе
учтены  все  недостатки, присущие  «традиционным» двухполюсным схемам,
что  позволило  принять  в  расчет  все  разнообразие  многофункциональных
свойств системы и свести к минимуму погрешность в оценке характеристик
надежности объекта.

В процессе построения структурно-функциональных схем составле-

ны критерии и выполнена систематизация элементов ПЭД с учетом взаимно-
го влияния конструктивных элементов, геометрических параметров
и структурно-функциональных связей между ними, что позволило составить
математические модели вероятности возникновения отказа для узлов ПЭД.

Составлены математические модели вероятности возникновения

отказа для основных узлов ПЭД, а именно: упорного подшипника, токоввода
и обмотки статора, ротора, магнитопровода статора, нижнего основания
ПЭД, учитывающие влияние магнитных, электрических, механических, кон-
структивных факторов и связей на эксплуатационную эффективность ПЭД.

В результате комплекса преобразований математических моделей

узлов ПЭД получено выражение для вероятности возникновения отказа
погружного электродвигателя в общей форме.

Составлена композиционная модель оценки эффективности эксплуа-

тации элементов конструкции ПЭУ. Она позволит вносить коррективы
в существующие гипотезы и достигать адекватных оценок параметров на-
дежности в процессе эксплуатации оборудования ПЭУ и, как следствие, мо-
дифицировать существующие параметры и подходы ТОиР.

По результатам интеллектуального исследования, математических вы-

числений и анализа полученных данных получена математическая модель,

Повышение эффективности эксплуатации

погружных электроустановок нефтедобычи

146

в которой полно отражен процесс возникновения отказа элемента и конст-
руктивно учитывается взаимосвязь количества отказов с эффективностью
эксплуатации и количеством находящихся в работе однотипных элементов.

Составлены математические модели, позволяющие произвести оцен-

ку параметров различных законов распределения отказов элементов ПЭД
и представить в численном виде характеристики внезапных и релакса-
ционных отказов.

Оригинал статьи: Глава пятая. Разработка и исследование математической модели эксплуатационной эффективности ПЭД

Читать онлайн

5.1. Классификация элементов ПЭД как сложной технической системы
5.2. Формирование математической модели ПЭД в виде структурно-функциональной схемы
5.3. Оценка параметров постулируемых законов распределения постепенных отказов деталей в процессе эксплуатации
5.4. Определение уточненных уровней эксплуатационной эффективности элементов ПЭД при различных законах распределения отказов
5.5. Выводы по главе

Все анонсы