12
управление сетями
Геометрия уравнений
установившихся режимов
электрической системы
УДК 621.316.1
Представлена
геометрическая
интерпретация
множества
всех
решений
урав
-
нений
установившихся
режимов
электрической
системы
(
для
заданных
пара
-
метров
системы
)
как
гиперповерхность
в
пространстве
узловых
мощностей
,
а
области
существования
режимов
—
как
проекция
этой
гиперповерхности
вдоль
оси
активной
мощности
балансирующего
узла
на
подпространство
задаваемых
узловых
мощностей
.
Показано
влияние
месторасположения
балансирующего
узла
на
получаемые
предельные
режимы
,
расчетную
область
существования
режимов
и
ее
односвязанность
.
Давыдов
В
.
В
.,
к.т.н., доцент, ведущий
специалист филиала
АО «СО ЕЭС» —
ОДУ Сибири
Ерохин
П
.
М
.,
д.т.н., доцент,
советник директора
АО «СО ЕЭС»
Ключевые
слова
:
балансирующий узел,
гиперповерхность
мощностей, область
существования
режимов, предельный
режим, установившийся
режим, электрическая
система
ВВЕДЕНИЕ
Расчеты установившихся режимов (УР) электрических систем (ЭС) играют
особую роль в теории и практике управления режимами ЭС, непосредствен-
но или опосредовано используются практически во всех областях совре-
менной теории режимов ЭС, составляя ее скелет. К настоящему времени
большинство опубликованных работ посвящены, как правило, разработке
и реализации методов расчета потокораспределения, то есть численному
решению систем нелинейных уравнений УР ЭС [1]. Математичес кие соот-
ношения и выражения являются хорошими инструментариями для числен-
ного решения, однако сложны для качественного анализа. Вместе с тем
развитие теории бифуркации, особенностей и катастроф показывает, что
геометрическое рассмотрение позволяет воспользоваться мощными сред-
ствами современной геометрии и получить качественно новые интересные
результаты [2]. Хотя рядом авторов проводились исследования областей
существования решения уравнений УР, однако они, как правило, ограничи-
вались небольшими, в основном трехузловыми моделями ЭС [3–7], часто
консервативными [8–9], используя геометрические построения только для
отображения численных результатов или пояснения предлагаемых подхо-
дов. Целью данной работы является геометрическая интерпретация мно-
жества всех решений уравнений УР ЭС (для заданных параметров систе-
мы) как гиперповерхности в пространстве мощностей узлов.
ГИПЕРПОВЕРХНОСТЬ
МОЩНОСТЕЙ
И
ОБЛАСТЬ
СУЩЕСТВОВАНИЯ
УСТАНОВИВШИХСЯ
РЕЖИМОВ
ЭЛЕКТРИЧЕСКОЙ
СИСТЕМЫ
В теории электрических систем существует ряд математических моде-
лей потокораспределения, каждая из которых основывается на уравне-
ниях законов Кирхгофа, имеет определенные преимущества и недостат-
ки и может быть получена из другой математическим преобразованием.
Поэтому качественные выводы и заключения, полученные на одной
модели, остаются справедливыми также и для других моделей потоко-
распределения. Рассмотрим систему уравнений УР в форме баланса
мощностей в смешанной системе координат (прямоугольная — для эле-
ментов матрицы узловых проводимостей
Y
km
=
G
km
+
jB
km
и трехфазных
мощностей
S
k
=
P
k
+
jQ
k
, а полярная — для комплексов линейных на-
пряжений
U
k
=
V
k
e
j
k
), которая для трехфазной симметричной сети может
быть представлена в следующем виде:
(
)
(
)
,
0
sin
cos
0
sin
cos
=
−
+
=
'
=
+
−
=
'
¦
¦
m
km
km
km
km
m
k
k
k
m
km
km
km
km
m
k
k
k
G
B
V
V
Q
Q
;
B
G
V
V
P
P
G
G
G
G
(1)
где
km
=
k
–
m
— разность фазовых углов между смежными узлами.
13
Система (1) пред-
ставляет собой уравне-
ния узловых балансов
активных и реактивных
мощностей,
которые
в УР, согласно законам
Кирхгофа, должны под-
держиваться в каждом
узле. Расчет режима
соответствует решению
системы нелинейных
уравнений УР (1), при
этом полагается, что
параметры системы, то
есть элементы матри-
цы узловых проводи-
мостей, известны, и УР
в каждом узле пред-
ставляется четырьмя
параметрами режима
(переменными):
P
k
,
Q
k
,
V
k
и
k
. Согласно (1) для
каждого узла имеется
два уравнения балан-
са активной и реактивной мощности. Поэтому для
того, чтобы рассчитать УР ЭС, для каждого узла
обязательно должны быть заданы два параметра.
С математической точки зрения отнесение к за-
висимым и независимым переменным может быть
произвольным, определяется только количество
зависимых переменных, значения которых могут
быть получены из решения (1) при известных неза-
висимых переменных. С точки зрения расчета УР
к независимым переменным относятся те, для ко-
торых имеется конкретная информация, а именно:
мощности узлов, а также модули напряжений ге-
нераторов, оснащенных системой АРВ. Комплексы
напряжений относятся к зависимым переменным,
которые находятся из решения (1).
Система нелинейных уравнений УР (1) имеет
важное свойство — изменение всех фазовых углов
на одну и ту же величину не оказывает на нее ника-
кого воздействия. Как следствие, такая система име-
ет бесконечное множество решений. Поэтому для
получения численного решения необходимо задать
точку отсчета, для чего фазовый угол одного из уз-
лов, который получает название базисного, должен
быть зафиксирован, то есть переведен в состав не-
зависимых переменных. Поскольку число зависимых
переменных становится на единицу меньше числа
уравнений, математическая формализация требует
пополнить их число. В силу специфики энергосистем
в качестве таковой принимается активная мощность
одного из узлов, который становится балансирую-
щим по активной мощности. Поскольку активная
мощность балансирующего узла
P
b
является зави-
симой переменной, она является функцией задава-
емых мощностей других узлов. График этой функции
P
b
=
P
b
(
P
,
Q
) представляет собой гиперповерхность
в пространстве мощностей — гиперповерхность
мощностей установившихся режимов ЭС (ГМ).
Гиперповерхность мощностей определяет всю со-
вокупность УР ЭС, в том числе гипотетических ста-
тически неустойчивых режимов, при неизменных па-
раметрах системы и заданных других независимых
переменных. Вне ГМ (внутри или снаружи) не суще-
ствуют никакие УР при заданных параметрах систе-
мы и режима. Любая точка ГМ отвечает конкретному
УР, ее координаты соответствуют мощностям узлов
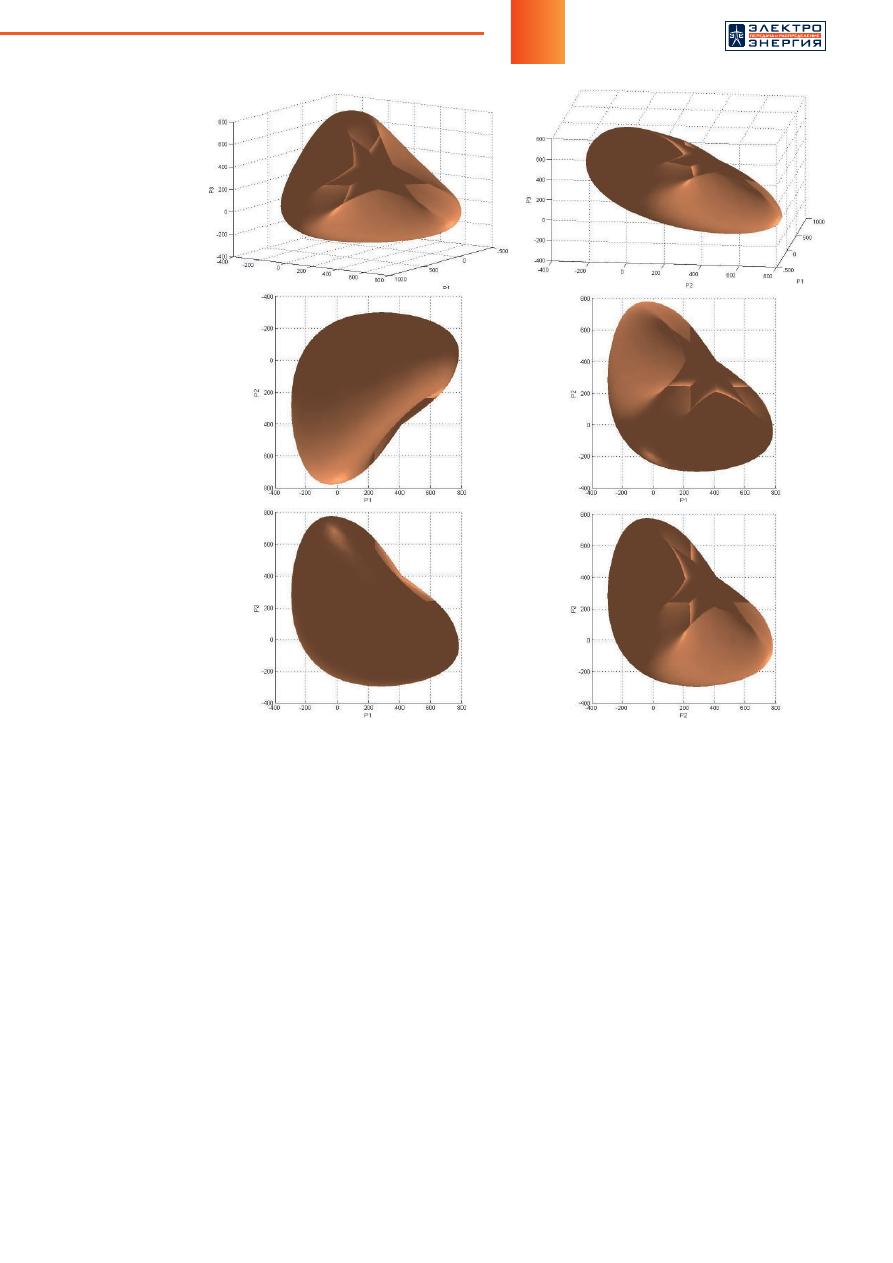
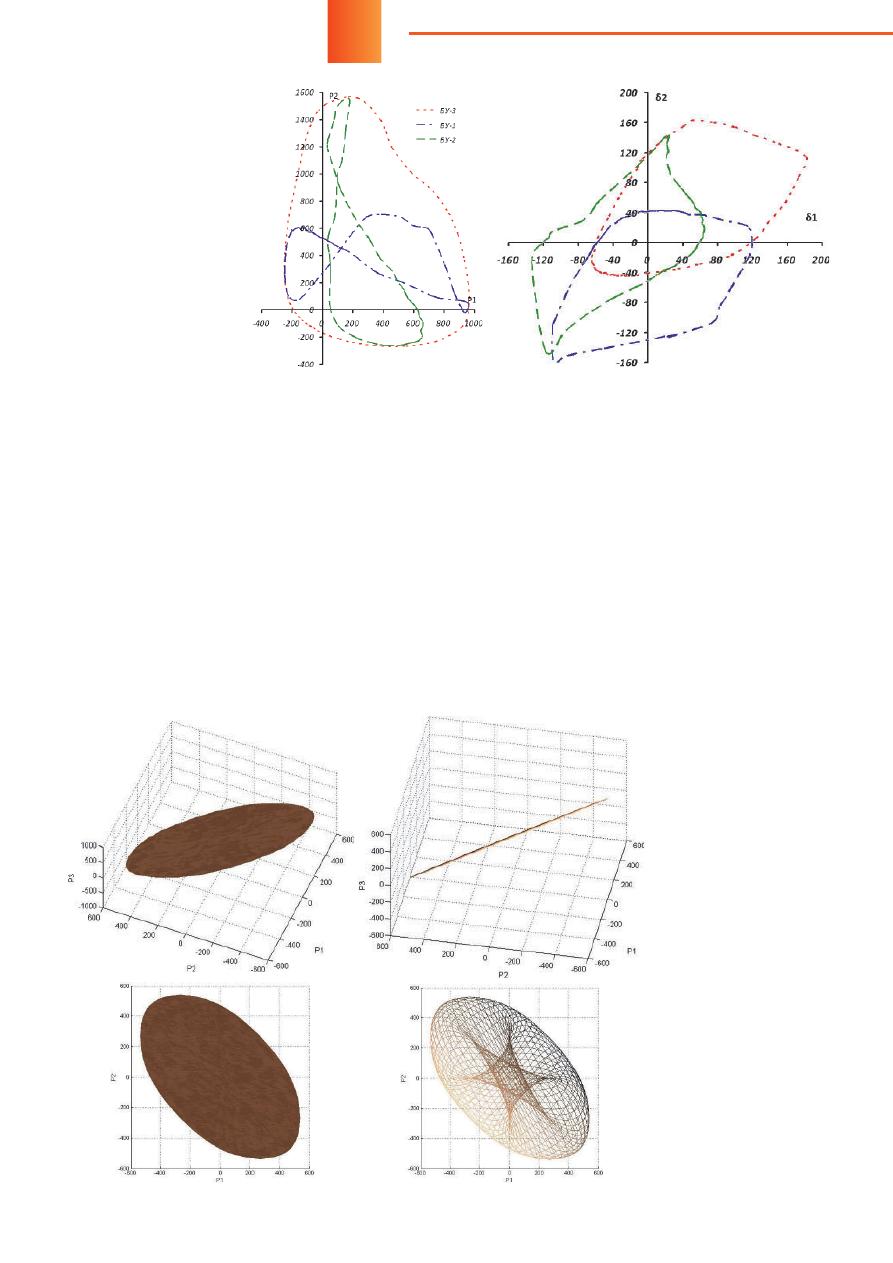
в этом режиме. В качестве примера на рисунке 1 пред-
ставлена ГМ трехузловой ЭС с
PV
-узлами с параме-
трами
V
1
=
V
2
=
V
3
= 110 кВ,
Z
12
=
Z
13
=
Z
23
= 20 +
j
40 Ом
и ее проекции сверху и снизу на соответствующие
координатные плоскости.
Обычно в теории и анализе УР используется поня-
тие области существования установившихся режимов
ЭС (ОСР). Так как ГМ определяет всю совокупность
УР ЭС для заданных параметров системы, ее про-
Рис
. 1.
Гиперповерхность
мощностей
трех
-
узловой
ЭС
(
а
,
б
)
и
ее
проекции
(
в
,
д
—
снизу
;
г
,
е
—
сверху
)
на
соответ
-
ствующие
коорди
-
натные
плос
кости
а)
б)
в)
д)
г)
е)
№
2 (53) 2019
14
екция на подпростран-
ство задаваемых узло-
вых мощностей вдоль
оси активной мощности
балансирующего узла
(БУ) является ничем
иным, как ОСР при со-
ответствующем
БУ,
а граница этой проек-
ции представляет со-
бой гиперповерхность
предельных режимов
(ПР) в пространстве
задаваемых узловых
мощностей. Таким об-
разом,
представлен-
ные на рисунках 1в–е
проекции ГМ являются
ОСР этой ЭС при БУ-3, БУ-2 и БУ-1 соответственно.
Так как в общем случае ГМ не является плоской,
ее проекция, то есть ОСР, и ее границы, то есть ГПР,
будут зависеть от выбора оси, вдоль которой осу-
ществляется ее проецирование, то есть от выбора
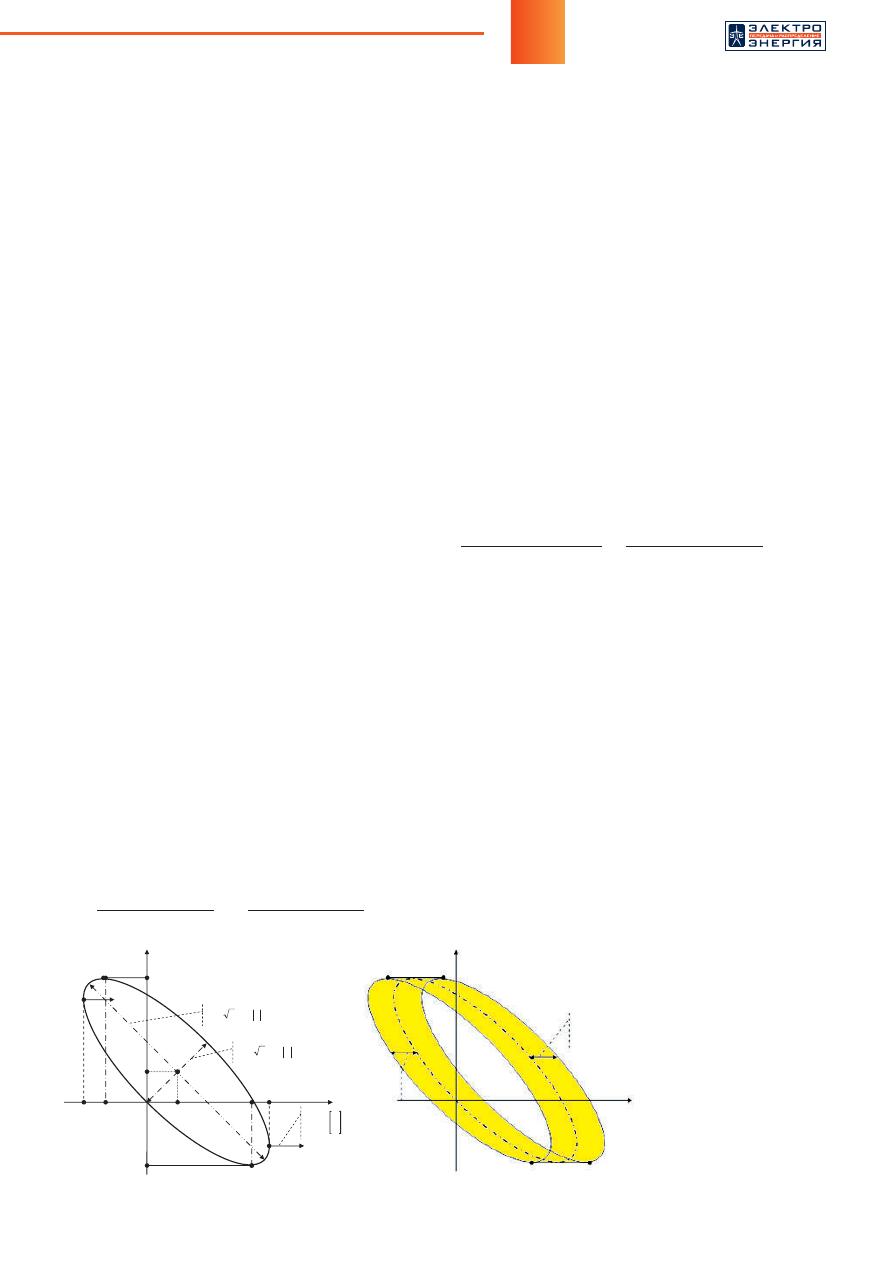
БУ. В качестве примера на рисунке 2а представлены
линии предельных режимов четырехузловой коль-
цевой схемы с тремя
PV
-узлами и одним
PQ
-узлом,
спроецированные на координатную плоскость мощ-
ностей двух
PV
-узлов при варьировании мощно-
стей в
PV
-узлах и неизменной мощности нагрузки
в
PQ
-узле. Каждая линия соответствует назначению
балансирующим одного из трех
PV
-узлов. На рисун-
ке 2б эти линии, которые также соответствуют вы-
рожденности матрицы Якоби потокораспределения
при соответствующем БУ, представлены в простран-
стве углов. Параметры этой четырехузловой систе-
мы следующие:
V
1
= 107 кВ;
V
2
= 109 кВ;
V
3
= 113 кВ;
P
4
= –60 –
j
46 МВА;
Z
12
= 19,11 +
j
32,994 Ом;
Z
14
= 5,681 +
j
8,379 Ом;
Z
23
= 19,536 +
j
14,916 Ом;
Z
34
= 13,386 +
j
28,635 Ом. Таким образом, исполь-
зование ГМ и рассмотрение ОСР как проекции ГМ
вдоль оси активной мощности БУ на подпростран-
ство мощностей остальных узлов обнаруживает,
что вид ОСР, ее граница, то есть ПР, зависят от
выбора БУ.
ГМ консервативной ЭС представляет собой «пло-
скую» гиперповерхность, так как отсутствуют потери
активной мощности, и мощности узлов удовлетво-
ряют уравнению
P
k
= 0. На рисунке 3 в качестве
примера показана ГМ трехузловой консервативной
ЭС (
Z
12
=
Z
13
=
Z
23
=
j
45 Ом) с
PV
-узлами и ее ОСР.
На рисунках 3а и 3б
представлен вид ГМ
с разных ракурсов. Эта
ГМ представляет собой
«плоский» эллипсоид.
Только край «плоской»
ГМ соответствуют ПР
и только его проекция
вдоль оси активной
мощности любого БУ на
подпространство всех
других узловых мощно-
стей является границей
ОСР
консервативной
ЭС. Поэтому ПР консер-
вативной ЭС не зависят
от месторасположения
БУ. На рисунке 3в пред-
ставлена ОСР при БУ-3.
На рисунке 3г та же ОСР
представлена в виде
«прозрачной» каркас-
ной поверх ности.
Известно, что систе-
ма нелинейных уравне-
ний УР ЭС может иметь
несколько решений при
заданных исходных дан-
ных, одни из которых
Рис
. 2.
Линии
предельных
режимов
четырехузловой
кольцевой
ЭС
Рис
. 3.
Гиперповерхность
мощностей
(
а
,
б
)
и
области
существования
(
в
,
г
)
устано
-
вившихся
режимов
трехузловой
консервативной
ЭС
а)
б)
в)
а)
г)
б)
УПРАВЛЕНИЕ
СЕТЯМИ
15
статически устойчивые, другие нет. Если в ЭС все ли-
нии не являются чисто индуктивными, тогда количе-
ство решений соответствует количеству пересечений
ГМ вектором заданных мощностей, направленным
параллельно оси активной мощности БУ. В случае,
если имеются также чисто индуктивные сопротивле-
ния, то даже одна точка пересечения с ГМ может со-
ответствовать нескольким решениям.
Так, например, каждая точка «плоской» ГМ трехуз-
ловой консервативной ЭС с
PV
-узлами на рисунках 3в
и 3г отвечает одному решению на границе ОСР, двум
решениям — внутри ОСР, но вне шестиугольной звез-
ды, как бы «сформированной» наложением двух тре-
угольников, а внутри каждого такого треугольника еще
двум дополнительным решениям, причем только одно
решение является статически устойчивым. В области
пересечения треугольников шестиконечной звезды на
рисунке 3г каждая точка ГМ соответствует шести ре-
шениям, в том числе в начале координат [9], то есть
когда мощности всех узлов равны нулю. При нулевых
мощностях всех узлов, в двух решениях, в том чис-
ле статически устойчивом, потоки мощности в линиях
равны нулю. В других четырех решениях происходит
замкнутая циркуляция потока активной мощности
по контуру (при нулевых мощностях во всех узлах!),
причем сумма углов в линиях по контуру равна ±360°
(в зависимости от решения), а не 0°, как для обычных
УР. Исследования показали [10], что для кольцевой
шестиузловой позиционной модели некоторые такие
вторые решения могут быть статически устойчивыми,
при этом потери реактивной мощности в ЭС для них
значительно превышают потери обычного решения,
соответствующего реальному УР ЭС.
НЕОДНОСВЯЗАННАЯ
ОБЛАСТЬ
СУЩЕСТВОВАНИЯ
РЕЖИМОВ
Геометрическое рассмотрение всей совокупности УР
как ГМ ЭС позволяет выяснить причину возможного
появления «дырок» в ОСР, то есть неодносвязан-
ности множества УР ЭС в пространстве мощностей
[11]. Появления «дырок» в ОСР можно объяснить,
если рассмотреть представленную на рисунке 4а ГМ
двухузловой схемы с
PV
-узлами, которая является
эллипсом в 2-мерном пространстве мощностей [12].
1
2
2
2
2
1
2
2
2
2
1
1
2
2
1
2
2
2
2
1
1
=
¸¸
¹
·
¨¨
©
§
+
−
−
+
¸¸
¹
·
¨¨
©
§
−
+
−
B
V
V
G
V
P
G
V
P
G
V
V
G
V
P
G
V
P
, (2)
где
G
+
jB
— комплекс проводимости ветви, соединя-
ющей эти два узла.
Вне эллипса (внутри и снаружи), из-за несовмест-
ности уравнений УР, не существуют никакие УР двух-
узловой ЭС, поэтому множество значений мощно-
стей двух узлов является невыпуклым. Именно это
является одной из главных предпосылок появления
«дырок» в ОСР многоузловых ЭС. Поскольку проек-
ция эллипса на любую ось представляет собой от-
резок прямой сплошной линии, который и является
ОСР двухузловой ЭС при соответствующем БУ (от-
резок [
P
1
A
,
P
1
B
] горизонтальной оси при БУ-2; отрезок
[
P
2
C
,
P
2
D
] вертикальной оси при БУ-1), множество УР
двухузловой ЭС конечно будет односвязанным. Не-
односвязанность может появиться уже в случае трех-
узловой ЭС, например, если добавить к этой двух-
узловой ЭС третий
PV
-узел, соединив его с первым
узлом, например, через индуктивное сопротивление
X
13
, и назначить его балансирующим. В этой трехуз-
ловой радиальной ЭС все узлы являются
PV
-узлами,
причем вся активная мощность БУ-3 напрямую без
потерь транспортируется к узлу 1. Поэтому, вос-
пользовавшись (2), ГМ такой ЭС можно представить
уравнением:
1
2
)
(
2
)
(
2
2
1
2
2
2
2
1
3
1
2
2
1
2
2
2
2
1
3
1
=
¸¸
¹
·
¨¨
©
§
+
−
−
+
+
¸¸
¹
·
¨¨
©
§
−
+
−
+
B
V
V
G
V
P
G
V
P
P
G
V
V
G
V
P
G
V
P
P
, (3)
где
P
3
=
P
31
= (
V
1
V
3
/
X
13
)
sin
31
.
Выражение (3) является уравнением поверхности
в трехмерном пространстве мощностей, проекция ко-
торой на плоскость
P
1
×
P
2
мощностей узлов 1 и 2 пред-
ставляет собой ОСР этой ЭС при БУ-3 (рисунок 4б).
Сравнение (3) с (2) показывает, что эллипс (3) для
конкретного
P
3
— это тот же эллипс (2), как на рисун-
ке 4а, только смещенный горизонтально на величину
мощности влево, если узел 1 получает мощность
от БУ-3, и вправо — в противном случае. Следова-
тельно, выражение (3) можно рассматривать как се-
мейство эллипсов на плоскости
P
1
×
P
2
. Поэтому ОСР
этой ЭС представляет собой область, заполняемую
эллипсами (3). Ее граница, то есть ПР, представляет
собой огибающую семейства эллипсов (3).
Максимальное и минимальное значение мощно-
сти, которую узел 1 может получить от БУ-3, опре-
деляется выражением
P
1
m
3
ax
=
V
1
V
3
/
X
13
= –
P
1
m
3
in
. По-
этому внешней границей ОСР является граница
выпуклой оболочки двух крайних эллипсов, смещен-
ных влево и вправо
горизонтально относи-
тельно центрального
эллипса (2) на величи-
ну
P
1
m
3
ax
=
V
1
V
3
/
X
13
, то
есть замкнутая кривая
A-B-C-D-A на рисун-
ке 4б. «Дырка» в ОСР
этой ЭС представляет
собой область пере-
сечения двух крайних
эллипсов, то есть об-
ласть, ограниченную
двумя дугами
EF
этих
эллипсов. Интересно
отметить, что ОСР этой
Рис
. 4.
Гиперповерхность
мощностей
(
а
)
двухузловой
ЭС
и
неодносвязанная
ОСР
(
б
)
трехузловой
радиальной
ЭС
с
PV-
узлами
1
P
2
P
C
A
P
P
1
1
B
D
P
P
1
1
G
V
2
1
G
V
2
2
G
V
V
2
1
2
B
V
V
2
1
2
2×
2×
A
C
D
B
0
1
P
0
C
P
2
D
P
2
O
=
а)
б)
V
1
V
3
P
1
m
3
ax
= —
X
13
P
2
P
1
A
B
E
F
D
C
V
1
V
3
|P
1
m
3
in
|
= —
X
13
№
2 (53) 2019
16
ЭС будет без «дырок»,
если БУ будет назна-
чен любой другой узел.
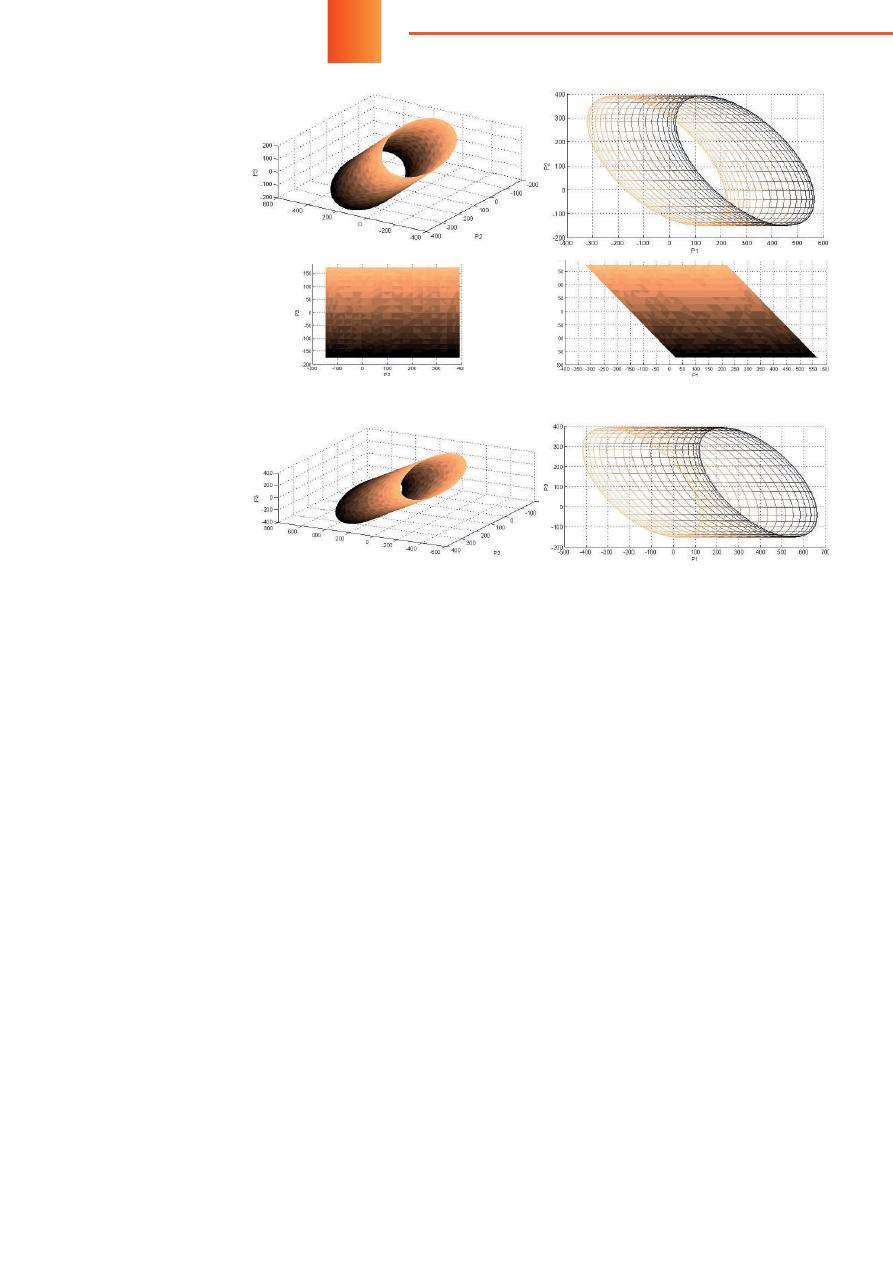
На рисунке 5 пред-
ставлены ГМ и ОСР
трехузловой радиаль-
ной ЭС с параметрами
V
1
=
V
2
=
V
3
= 110 кВ,
Z
12
= 20 +
j
40 Ом,
Z
13
=
j
70 Ом при раз-
личном назначении БУ.
Согласно
рисунку
5а, ГМ этой ЭС пред-
ставляет собой полый
эллипсовидный
ци-
линдр. Проекция ГМ
вдоль оси активной
мощности узла 3 пред-
ставлена на рисунке 5б,
имеет вид, аналогич-
ный рисунку 4б, и явля-
ется ОСР этой ЭС при
назначении БУ-3. Если
узел 1 будет назначен
балансирующим, это
фактически означает
разделение ЭС на две
подсистемы, режимы
которых не зависят друг на друга. Работа первой
подсистемы определяется только режимом узла 2,
а другой — режимом узла 3. Отсюда следует, что мно-
жеством УР ЭС будет область, ограниченная прямо-
угольником, длина сторон которого определяются
максимальными величинами мощности, получаемы-
ми/выдаваемыми из/в БУ узлами 2 и 3 соответствен-
но, как представлено на рисунке 5в. Если узел 2 будет
назначен балансирующим, ОСР будет ограничена па-
раллелограммом, как показано на рисунке 5г.
Если уменьшить величину индуктивного сопро-
тивления
Z
13
до
j
45 Ом, усилив электрическую связь
узла 1 с БУ-3, то тогда, хотя ГМ также будет представ-
лять собой эллипсовидный полый цилиндр (рисунок
6а), крайние эллипсы на плоскости
P
1
×
P
2
пересекать-
ся не будут, и «дырка» в ОСР исчезнет, как показано
на рисунке 6б. ОСР при других БУ качественно не
изменятся и будут аналогичны раннее представлен-
ным на рисунках 5в и 5г.
БАЛАНСИРУЮЩИЙ
УЗЕЛ
Гиперповерхность мощностей ЭС позволяет дать
геометрическое объяснение, почему для расчета УР
необходимо обязательно использовать БУ, то есть ак-
тивную мощность одного из узлов не задавать, а рас-
сматривать как переменную. Обычно такую необходи-
мость объясняют тем [13], что до расчета УР точное
значение потерь не известно. Поэтому невозможно
задать мощности узлов точно, чтобы обеспечить со-
вместность уравнений УР, то есть их разрешимость.
Но такое рассмотрение не может объяснить, почему
для расчета УР консервативной (то есть без потерь
активной мощности) ЭС со всеми
PV
-узлами, все рав-
но требуется БУ. В консервативной ЭС потери актив-
ной мощности равны нулю, поэтому задать активные
мощности во всех узлах, чтобы обеспечить совмест-
ность уравнений УР, довольно легко, однако без БУ
расчет режима невозможен. Причину этого довольно
легко объяснить с помощью ГМ. Каждый УР ЭС соот-
ветствует определенной точке на ГМ и наоборот. ГМ
есть отображение всей совокупности УР ЭС, в том
числе гипотетических (неустойчивых), в пространстве
узловых мощностей. Вне ГМ УР не существуют. Как
любая гиперповерхность, ГМ имеет меру ноль в рас-
сматриваемом пространстве. С точки зрения теории
вероятности это означает, что шанс задать коорди-
наты точки на ГМ (мощности узлов) без принятия во
внимание их функциональной зависимости так, чтобы
они отвечали уравнению гиперповерхности (уравне-
ниям потокораспределения), равен нулю. Поэтому,
чтобы получить координаты точки на ГМ (то есть рас-
считать режим), необходимо рассматривать одну из
координат этой точки (активную мощность балансиру-
ющего узла) как зависимую переменную. Поэтому все
вычислительные модели, которые используют урав-
нения УР, всегда применяют явно или неявно БУ — не
только модели расчета УР, но также вычислительные
модели оптимизации режима, оценки состояния, ста-
тической устойчивости и т.д.
ВЫВОДЫ
1. Вся совокупность установившихся режимов (УР)
электрических систем (ЭС) (для заданных параме-
тров системы) геометрически представляет собой
гиперповерхность в пространстве активных мощно-
стей всех узлов и реактивных мощностей
PQ
-узлов —
гиперповерхность мощностей УР ЭС (ГМ).
2. Область существования УР ЭС (ОСР) в про-
странстве мощностей, широко распространенная
в теории и анализе УР, является ничем иным, как
Рис
. 5.
Гиперповерхность
мощностей
(
а
)
трехузловой
ЭС
и
ОСР
с
«
дыркой
» (
б
)
при
БУ
-3;
ОСР
при
БУ
-1 (
в
)
и
БУ
-2 (
г
)
Рис
. 5.
Гиперповерхность
мощностей
(
а
)
трехузловой
ЭС
и
ОСР
(
б
)
при
БУ
-3
в)
а)
а)
г)
б)
б)
УПРАВЛЕНИЕ
СЕТЯМИ

17
ЛИТЕРАТУРА
1. Аюев Б.И., Давыдов В.В., Ерохин
П.М., Неуймин В.Г. Вычислитель-
ные модели потокораспределе-
ния в электрических системах. М.:
Флинта: Наука, 2008. 256 с.
2. Арнольд В.И. Теория катастроф.
М.: Наука, 1990. 128 с.
3. Идельчик В.И. Предел по суще-
ствованию решения уравнений
установившихся режимов / Вопро-
сы применения методов при управ-
лении режимами и развитием элек-
трических систем. Иркутск: ИПИ,
1975. С. 6–21.
4. Идельчик В.И. Расчеты установив-
шихся режимов электрических си-
стем. М.: Энергия, 1977. 192 с.
5. Виноградов А.А., Идельчик В.И.,
Лазебник А.И. Расчетное исследо-
вание области существования ре-
шения уравнений установившегося
режима и соотношения между пре-
делами по существованию и стати-
ческой апериодической устойчиво-
сти / Вопросы применения методов
при управлении режимами и раз-
витием электрических систем. Ир-
кутск: ИПИ, 1975. С. 22–49.
6. Тарасов В.И. Теоретические ос-
новы анализа установившихся
режимов электроэнергетических
систем. Новосибирск: Наука, 2002.
344 с.
7. Hiskens I.A., Davy R.J. Exploring the
Power Flow Solution Space Bound-
ary. IEEE Trans. Power Syst., vol. 16,
no. 3, pp. 389-395, Aug. 2001.
8. Рудницкий М.П. Элементы теории
устойчивости и управления режи-
мами энергосистем. Учебное по-
собие. Свердловск: Изд. УПИ им.
С.М. Кирова, 1984. 96 с.
9. Tavora C.J., Smith O.J.M. Equilibrium
Analysis of Power Systems. IEEE
Trans. PAS-91, 1972, vol. 91, no. 3,
pp. 1131-1137.
10. Korsak A.J. On the Question of
Uniqueness of Stable Load-fl ow So-
lutions. IEEE Trans. PAS-91, May/
June 1972, pp. 1093-1100.
11. Васин В.П. Области существо-
вания установившихся режимов
электрических систем. Учебное по-
собие. М.: МЭИ, 1982. 84 с.
12. Давыдов В.В., Ерохин П.М., Кири-
лов К.Ю. Гиперповерхность мощ-
ностей установившихся режимов
электрической системы / Электро-
энергетика глазами молодежи: на-
учн. тр. III междунар. науч.-техн.
конф. г. Екатеринбург, 22–26 ок-
тября 2012 г. В 2 т. Екатеринбург:
УрФУ, 2012. Т. 1. С. 191–197.
13. Stott B. Review of Load-fl ow Calcula-
tion Methods. Proc. IEEE, July 1974,
vol. 62, no. 7, pp. 916-929.
REFERENCES
1. Ayuyev B.I., Davydov V.V., Erokhin
P.M., Neuymin V.G.
Vychislitelnyye
modeli potokoraspredeleniya v elek-
tricheskikh sistemakh
[Computational
models of power fl ow distribution in
electrical systems]. Moscow, Flinta:
Nauka Publ., 2008. 256 p.
2. Arnold V.I.
Teoriya katastrof
[Catas-
trophe theory]. Moscow, Nauka Publ.,
1990. 128 p.
3. Idelchik V.I.
Predel po sushchest-
vovaniyu resheniya uravneniy usta-
novivshikhsya rezhimov. Voprosy
primeneniya metodov pri upravlenii
rezhimami i razvitiyem elektricheskikh
system
[Limit on the existence of
equations solution for steady-state
modes. Issues of methods application
when managing modes and develop-
ment of electrical systems]. Irkutsk,
INRTU Publ., 1975. 230 p.
4. Idelchik V.I. Calculations of steady-
state modes in electrical systems.
Moscow, Energiya Publ., 1977. 192 p.
5. Vinogradov A.A., Idelchik V.I., Lazeb-
nik A.I. Computational study of exis-
tence domain for steady-state mode
equations solution and research of
the relationship between existence
limits of static and aperiodic stability.
Issues of methods application when
managing modes and development
of electrical systems. Irkutsk, INRTU
Publ., 1975. 230 p.
6. Tarasov V.I.
Teoreticheskiye osnovy
analiza ustanovivshikhsya rezhimov
elektroenergeticheskikh system
[The-
oretical bases of steady-state modeв
analysis in electric power systems].
Novosibirsk, Nauka Publ., 2002.
344 p.
7. Hiskens I.A., Davy R.J. Exploring the
Power Flow Solution Space Bound-
ary. IEEE Trans. Power Syst., vol. 16,
no. 3, pp. 389-395, Aug. 2001.
8. Rudnitskiy M.P.
Elementy teorii us-
toychivosti i upravleniya rezhimami
energosistem
[Elements of the theory
of power systems stability and con-
trol]. Sverdlovsk, Ural State Technical
University Publ., 1984. 96 p.
9. Tavora C.J., Smith O.J.M. Equilibrium
Analysis of Power Systems. IEEE
Trans. PAS-91, 1972, vol. 91, no. 3,
pp. 1131-1137.
10. Korsak A.J. On the Question of
Uniqueness of Stable Load-fl ow So-
lutions. IEEE Trans. PAS-91, May/
June 1972, pp. 1093-1100.
11. Vasin V.P.
Oblasti sushchestvovaniya
ustanovivshikhsya rezhimov elek-
tricheskikh system
[Areas of electri-
cal systems steady state modes ex-
istence]. Moscow, MPEI Publ., 1982.
84 p.
12. Davydov V.V., Erokhin P.M., Kirilov
K.Yu. The hypersurface of powers for
electrical system steady state modes.
III Mezhdunarodnaya molodezhnaya
nauchno-tekhnicheskaya konferen-
tsiya "Elektroyenergetika glazami
molodezhi"
[III International scien-
tifi c-technical conference "Electrical
Power Engineering: Viewpoint of the
Youth"]. Ekaterinburg, 2012, vol. 1,
pp. 191–197. (In Russian)
13. Stott B. Review of Load-fl ow Calcula-
tion Methods. Proc. IEEE, July 1974,
vol. 62, no. 7, pp. 916-929.
проекцией ГМ вдоль оси активной мощности ба-
лансирующего узла (БУ) на подпространство за-
даваемых мощностей, а граница этой проекции —
гиперповерхностью предельных режимов (ПР)
в пространстве мощностей. Так как в общем случае
ГМ не является плоской, ее проекция, то есть ОСР,
и ее границы, то есть гиперповерхность ПР, будут
зависеть от выбора оси, вдоль которой осущест-
вляется ее проецирование, то есть от выбора БУ.
Для консервативной модели ЭС ГМ является «пло-
ской», поэтому ее ОСР и гиперповерхность ПР не
зависят от выбора БУ.
3. ГМ позволила наглядно объяснить механизм по-
явления «дырок» в ОСР, то есть неодносвязанности
множества режимов ЭС в пространстве мощностей,
а также исчезновение этих дырок при переназна-
чении БУ.
4. Рассмотрение всех совокупностей УР ЭС как ГМ
дает возможность воспользоваться инструментари-
ями теории бифуркации, особенностей и катастроф
(интерпретируя ГМ как поверхность равновесий («ка-
тастроф») в терминах этих теорий) для дальнейшего
исследования специфики, структуры ОСР, влияния
балансирующего узла.
№
2 (53) 2019
Оригинал статьи: Геометрия уравнений установившихся режимов электрической системы
Представлена геометрическая интерпретация множества всех решений уравнений установившихся режимов электрической системы (для заданных параметров системы) как гиперповерхность в пространстве узловых мощностей, а области существования режимов — как проекция этой гиперповерхности вдоль оси активной мощности балансирующего узла на подпространство задаваемых узловых мощностей. Показано влияние месторасположения балансирующего узла на получаемые предельные режимы, расчетную область существования режимов и ее односвязанность.