Энергетические процессы активного электромагнитного подвеса

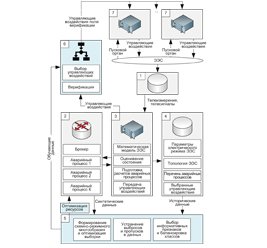
Использование активного магнитного подвеса роторов быстроходных энергетических машин — одно из перспективных направлений совершенствования роторных агрегатов, благодаря возможности существенно повысить энергетическую эффективность мощных вращающихся машин (электродвигателей, компрессоров, ультрацентрифуг) за счет снижения потерь на трение в подшипниковых узлах. В статье рассматриваются специфические энергетические процессы, происходящие в активном радиальном электромагнитном подшипнике мощного газонагнетателя, исследованы виды основных и добавочных потерь, возникающих при его работе. Методом математического моделирования уточнены значения потерь в магнитопроводе ротора, возникающих в результате его вращения в магнитном поле электромагнитов, потерь, вызванных откликом системы управления на стабилизацию ротора в пространстве, потерь от несущей частоты широтно-импульсного модулирования. Даны рекомендации для повышения энергетической эффективности преобразования энергии в элементах активного магнитного подвеса на примере газонагнетателя магистрального газоперекачивающего агрегата.