100
Д
ля
электрических
сетей
важной
и
актуаль
-
ной
является
задача
определения
места
повреждения
(
ОМП
) [1, 2].
В
электрических
сетях
класса
напряжения
110
кВ
и
выше
раз
-
работано
много
методов
и
дистанционных
приборов
ОМП
.
В
этих
сетях
длины
линий
и
отклю
-
чающие
мощности
велики
.
Поэтому
в
этих
сетях
оправдано
применение
дорогостоящих
приборов
ОМП
.
Например
,
прибор
Сириус
-2-
ОМП
[3].
В
его
па
-
спорте
указано
,
что
он
предназначен
для
электри
-
ческих
сетей
6–750
кВ
.
Однако
сети
110
кВ
и
выше
эксплуатируются
с
глухозаземленной
нейтралью
,
а
сети
6–10–35
кВ
—
с
изолированной
нейтралью
.
Это
требует
своего
подхода
для
разработки
мето
-
дов
и
приборов
ОМП
в
сетях
6–10–35
кВ
.
Они
долж
-
ны
определять
все
возможные
аварийные
режимы
(
АР
)
и
иметь
приемлемую
стоимость
.
Приборы
ОМП
подразделяются
на
дистанцион
-
ные
и
топографические
[1, 2].
Дистанционные
по
-
зволяют
определять
место
повреждения
без
обхо
-
да
линий
,
а
топографические
требуют
обход
линии
.
Для
сетей
6–10–35
кВ
нет
эффективных
дистанци
-
онных
приборов
.
В
основном
применяются
топогра
-
фические
приборы
.
Одним
из
видов
дистанционных
приборов
являются
дистанционные
приборы
по
па
-
раметрам
аварийного
режима
.
В
основном
они
ис
-
пользуют
параметры
электрической
сети
,
а
также
напряжения
и
токи
в
определенных
точках
сети
.
Так
например
,
в
[3]
использованы
следующие
формулы
для
определения
расстояния
до
трехфазного
,
двух
-
фазного
и
однофазного
короткого
замыкания
(
КЗ
):
U
L
КЗС
(3)
= — ·
sin
3;
√
3 ·
I
КЗ
(3)
·
Z
ПР
U
L
КЗС
(2)
= — ·
sin
2;
√
3 ·
I
КЗ
(2)
·
Z
ПР
√
3 ·
U
L
КЗС
(1)
= — ·
sin
1.
I
КЗ
(1)
· (2
Z
ПР
+
Z
НУЛ
)
Эмпирические критерии
для определения
места повреждения
в электрических сетях 6 кВ
УДК
621.314:621.315
Солдатов
В
.
А
.,
д
.
т
.
н
.,
профессор
,
заве
дующий
кафедрой
информационных
технологий
в
электро
-
энергетике
ФГБОУ
ВО
«
Костром
-
ская
государственная
сельскохозяйственная
академия
»
Мозохин
А
.
Е
.,
к
.
т
.
н
.,
доцент
кафедры
автоматики
и
микро
-
процессорной
техники
ФГБОУ
ВО
«
Костром
-
ской
государственный
университет
»,
заме
-
ститель
начальника
отдела
эксплуатации
автома
тизированных
систем
диспетчерского
управления
филиала
ПАО
«
МРСК
Центра
» —
«
Костромаэнерго
»
Ключевые
слова
:
аварийные
режимы
,
сеть
6
кВ
,
определение
места
повреждения
,
эмпирические
критерии
,
интерполяционные
по
-
линомы
Keywords:
emergency modes in the
network, 6 kV networks,
fault location, empirical
criterion, interpolation
polynomial
Исследована
возможность
определения
места
повреждения
в
сетях
6
кВ
по
эмпирическим
критериям
для
разных
видов
аварийных
режимов
.
При
разработке
критериев
использова
-
ны
модули
фазных
напряжений
и
токов
в
начале
линии
6
кВ
.
Для
всех
разработанных
эмпирических
критериев
получены
их
интерполяционные
зависимости
от
точки
повреждения
вдоль
длины
линии
.
Показано
,
что
погрешность
определения
места
повреждения
для
всех
аварийных
режимов
не
превыша
-
ет
7%,
за
исключением
режима
обрыва
фазы
.
д
и
а
г
н
о
с
т
и
к
а
и
м
о
н
и
т
о
р
и
н
г
диагностика и мониторинг

101
В
этих
формулах
обозначено
:
U
—
напряжения
соответствующих
фаз
линии
;
Z
ПР
,
Z
НУЛ
—
модули
удельных
сопротивлений
прямой
и
нулевой
последо
-
вательности
;
I
КЗ
—
токи
соответствующих
фаз
линии
;
1,
2,
3 —
углы
между
приложенными
напряжени
-
ями
и
токами
для
соответствующих
КЗ
.
То
есть
существующие
приборы
ОМП
определяют
только
КЗ
и
не
определяют
АР
с
однофазными
замы
-
каниями
на
землю
и
с
обрывами
фаз
.
Чтобы
устра
-
нить
этот
недостаток
,
разработаем
индивидуальные
эмпирические
критерии
для
каждого
вида
АР
.
При
раз
-
работке
критериев
используем
модули
фазных
напря
-
жений
и
токов
в
начале
линии
6
кВ
.
При
перемещении
точки
повреждения
вдоль
длины
линии
некоторые
параметры
будут
увеличиваться
,
а
некоторые
умень
-
шаться
.
Для
получения
формулы
аналитического
критерия
увеличивающиеся
параметры
помещались
в
числитель
,
а
уменьшающиеся
—
в
знаменатель
[4].
Были
рассчитаны
следующие
АР
:
замыкания
фаз
на
землю
(
АО
,
ВО
,
СО
);
короткие
замыкания
между
фазами
(AB, AC, BC,
АВС
);
двойное
замыкание
фаз
на
землю
(
АО
-
ВО
,
АО
-
СО
,
ВО
-
СО
);
обрывы
фаз
(
обр
.
А
,
обр
.
В
,
обр
.
С
);
одновременное
замыкание
на
землю
и
обрыв
фаз
(AO +
обр
. A, BO +
обр
. B,
CO +
обр
.
С
);
одновременный
обрыв
и
замыкание
фаз
на
землю
(
обр
.
А
+
АО
,
обр
.
В
+
ВО
,
обр
.
С
+
СО
).
Здесь
буквой
О
обозначена
земля
.
При
расчетах
АР
применялся
метод
фазных
коор
-
динат
[5].
В
качестве
примера
приведем
полученные
критерии
только
для
АР
поврежденной
фазы
А
:
1.
Однофазное
замыкание
на
землю
(
АО
):
K
ao
=
U
a
/ (
U
b
·
U
c
).
2.
Короткое
замыкание
между
фазами
(
АВ
):
K
ab
= (
U
a
·
U
b
) / (
I
a
·
I
b
).
3.
Короткое
замыкание
между
фазами
(
АС
):
K
ac
= (
U
a
·
U
c
) / (
I
a
·
I
c
).
4.
Короткое
замыкание
между
фазами
(
АВС
):
K
ab
= (
U
a
·
U
b
·
U
c
) / (
I
a
·
I
b
·
I
c
).
5.
Двойное
замыкание
фаз
(
АО
-
ВО
):
K
aobo
= (
U
a
·
U
b
) / (
I
a
·
I
b
).
6.
Двойное
замыкание
фаз
(
АО
-
СО
):
K
aoco
= (
U
a
·
U
c
) / (
I
a
·
I
c
).
7.
Обрыв
фазы
(
обр
.
А
):
K
обр
.
A
=
U
a
·
U
c
·
I
a
/
U
a
.
8.
Одновременное
замыкание
на
землю
и
обрыв
фазы
(AO +
обр
.
А
):
K
ao
обр
.
A
=
U
a
.
9.
Одновременный
обрыв
и
замыкание
на
землю
фазы
(
обр
.
А
+ AO):
K
обр
.
Aao
=
I
a
.
Аналогичные
формулы
были
получены
для
АР
при
поврежденной
фазе
В
и
С
.
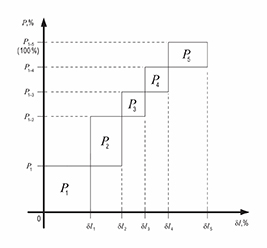
Из
таблицы
1
видно
,
что
при
перемещении
точ
-
ки
АР
вдоль
длины
линии
все
полученные
критерии
увеличиваются
.
Однако
значения
критериев
извест
-
ны
только
в
расчетных
точках
.
Чтобы
получить
гра
-
фики
изменения
этих
критериев
,
были
получены
их
интерполяционные
полиномы
от
точки
повреждения
вдоль
длины
линии
.
Интерполяционные
полиномы
получены
на
основе
матрицы
Вандермонда
[6].
Опи
-
шем
алгоритм
получения
этих
полиномов
.
1.
Задаются
вектор
-
столбцы
расстояний
L
и
зна
-
чений
критерия
(
например
,
для
режима
АО
)
для
каждой
расчетной
точки
n
вдоль
длины
линии
:
L
1
K
ao
1
L
2
K
ao
2
L
=
;
K
ao
=
.
...
...
L
n
K
aon
2.
Рассчитывается
матрица
Вандермонда
:
A
i
,
j
= (
L
i
)
n
–
j
,
где
A
—
квадратная
матрица
Вандермонда
;
L
i
—
i
-
й
элемент
вектор
-
столбца
L
;
n
—
количество
расчет
-
ных
точек
;
i
—
индекс
строки
матрицы
(
изменяется
от
1
до
n
);
j
—
индекс
столбца
матрицы
(
изменяется
от
1
до
n
).
3.
Определяются
коэффициенты
полинома
:
z
=
A
–1
·
K
ao
,
где
z
—
столбцовая
матрица
коэффициентов
поли
-
нома
;
A
–1
—
обратная
матрица
Вандермонда
;
K
ao
—
вектор
-
столбец
значений
критерия
.
Надо
отметить
,
что
матрица
Вандермонда
неосо
-
бенная
,
то
есть
обязательно
существует
ее
обратная
матрица
.
Из
этого
следует
,
что
коэффициенты
поли
-
нома
z
будут
всегда
определены
.
4.
Записывается
уравнение
полинома
:
n
P
(
x
) =
(
z
k
·
x
n
–
k
),
k
=
1
где
P
(
x
) —
уравнение
полинома
;
z
k
—
коэффициенты
полинома
;
x
—
координата
по
оси
L
.
Полином
P
(
x
)
пройдет
через
все
заданные
точки
значений
критерия
K
ao
.
Допустим
,
что
значения
критерия
будут
вычислять
-
ся
или
измеряться
с
погрешностью
.
Тогда
опреде
-
Табл
. 1.
Изменение
эмпирических
критериев
при
перемещении
точки
АР
вдоль
длины
линии
Точка
АР
,
км
Значения
эмпирических
критериев
K
ao
K
ab
K
ac
K
abc
K
aobo
K
aoco
K
обр
.
A
K
ao
обр
.
A
K
обр
.
Aao
0
0
0,20
0,15
0
0,009
0,009
1,80
0,03
0,005
5
2,39
7,98
8,11
1163,5
5,13
5,85
2,12
6,53
0,072
10
4,89
29,19
30,21
9175,4
19,96
22,77
2,72
13,03
0,145
15
7,51
63,66
66,37
30828,6
44,56
50,78
3,77
19,48
0,217
№
5 (50) 2018

102
лим
максимальную
U
i
'
и
минимальную
U
i
"
границы
расчетных
(
или
измеренных
)
величин
критерия
:
U
i
' =
U
i
+
·
U
i
,
U
i
" =
U
i
–
·
U
i
,
где
U
i
—
значение
расчетной
(
или
измеренной
)
вели
-
чины
критерия
.
Приравнивая
полином
P
(
x
)
значениям
U
i
'
и
U
i
",
по
-
лучим
два
уравнения
:
P
(
x
) =
U
i
';
P
(
x
) =
U
i
".
Из
этих
уравнений
получим
значения
левой
x
1
и
правой
x
2
границы
интервала
,
где
произошло
по
-
вреждение
.
Величина
самого
интервала
d
L
определится
как
:
d
L
=
x
1
–
x
2
.
Погрешность
определения
места
повреждения
будет
равна
:
d
L
= — · 100%,
L
S
где
L
S
—
длина
всей
линии
.
Используя
интерполяционные
полиномы
,
были
получены
значения
левой
x
1
и
правой
x
2
.
Результа
-
ты
расчетов
представлены
в
таблице
2.
Там
же
даны
погрешности
ОМП
d
L
в
километрах
и
в
процентах
по
отношению
к
длине
всей
линии
.
Расчеты
были
про
-
ведены
для
длины
линии
5
км
и
15
км
.
В
таблице
2
приведены
результаты
расчетов
только
при
длине
линии
15
км
и
возникновении
аварии
в
точке
10
км
от
начала
линии
.
Анализ
таблицы
2
показал
,
что
погрешность
ОМП
не
превышает
1
км
и
7%
от
длины
линии
.
Исключе
-
Табл
. 2.
Погрешность
ОМП
по
эмпирическим
критериям
Вид
АР
Начальная
и
конечная
величина
интервала
,
км
Погреш
-
ность
,
км
Погреш
-
ность
, %
x
1
x
2
d
L
d
L
A
О
10,477
9,521
0,955
6,37
B
О
10,479
9,519
0,96
6,40
C
О
10,48
9,518
0,962
6,41
AB
10,259
9,74
0,524
3,49
AC
10,256
9,74
0,519
3,46
BC
10,258
9,736
0,522
3,48
ние
составляют
режимы
обрыва
фаз
,
когда
погреш
-
ность
ОМП
достигает
14%.
Режимы
с
короткими
за
-
мыканиями
фаз
и
двойными
замыканиями
на
землю
не
превышают
4%.
Надо
отметить
,
что
для
сетей
6–10–35
кВ
существующие
приборы
ОМП
опреде
-
ляют
только
режимы
с
короткими
замыканиями
и
не
определяют
режимы
с
замыканиями
на
землю
и
об
-
рывами
фаз
.
При
этом
погрешность
ОМП
может
со
-
ставлять
от
5%
до
20%.
Таким
образом
,
разработанная
методика
ОМП
по
эмпирическим
критериям
позволяет
определять
расстояние
до
точки
повреждения
при
всех
возмож
-
ных
АР
с
достаточной
для
практического
примене
-
ния
погрешностью
не
более
7%,
за
исключением
режимов
обрыва
фаз
когда
погрешность
достигает
14%.
ДИАГНОСТИКА
И МОНИТОРИНГ
ЛИТЕРАТУРА
1.
Аржанников
Е
.
А
.
Методы
и
прибо
-
ры
определения
мест
поврежде
-
ния
на
линиях
электропередачи
/
Е
.
А
.
Аржанников
,
А
.
М
.
Чухин
.
М
.:
НТФ
«
Энергопресс
», 1998. 87
с
.
2.
Шалыт
Г
.
М
.
Определение
мест
по
-
вреждения
в
электрических
сетях
.
М
.:
Энергоиздат
, 1982. 312
с
.
3.
Устройство
определения
места
повреждения
на
воздушных
ли
-
ниях
электропередачи
«
Сириус
-2-
ОМП
».
Руководство
по
эксплуата
-
ции
.
М
., 2012. 64
с
.
4.
Солдатов
В
.
А
.,
Рысина
Н
.
Н
.
Опре
-
деление
места
повреждения
в
сельских
электрических
сетях
10
кВ
по
эмпирическим
критери
-
ям
/
Актуальные
вопросы
АПК
:
сборник
статей
заочной
междуна
-
родной
научно
-
практической
кон
-
ференции
молодых
ученых
.
Кара
-
ваево
:
Костромская
ГСХА
, 2016.
С
. 120–123.
5.
Лосев
С
.
Б
.
Об
использовании
фазных
координат
при
расчете
сложнонесимметричных
режи
-
мов
//
Электричество
, 1979,
№
1.
С
. 15–23.
6.
Заварыгин
В
.
М
.
Численные
мето
-
ды
.
М
.:
Просвещение
, 1991. 250
с
.
REFERENCES
1. Arzhannikov E.A., Chuhin A.M.
Me-
tody i pribory opredelenija mest po-
vrezh denija na linijah jelektroper-
edachi
[Methods and devices for
locating faults on transmission lines].
M.: Energo-press, 1998. 87 p.
2. Shalyt G.M.
Opredelenie mest po-
vrezhdeniya v ehlektricheskih setyah
[Determination of fault locations in
electrical networks]. M.: Energoizdat
[Energypublish], 1982, 312 p.
3.
Ustrojstvo opredeleniya mesta po-
vrezh deniya na vozdushnyh liniyah
ehlektroperedachi «Sirius-2-OMP»
[Device for locating damage on
Sirius-2-OMP power transmission
lines].
Rukovodstvo po ehkspluatacii
[Instruction manual]. M., 2012, 64 p.
4. Soldatov
V.A.
Opredelenie mesta po-
vrezhdeniya v sel'skih ehlektri ches-
kih setyah 10 kV po ehmpiriches-
kim kriteriyam
[Determination of the
fault location in rural electric net-
works of 10 kV by empirical criteria].
Aktual'nye voprosy APK: sbornik sta -
tej zaochnoj muzhdunarodnoj na uch-
no-prakticheskoj konferencii mo
lo-
dyh uchenyh
[Actual issues of the
agrarian and industrial complex:
a collection of articles of the corre-
spondence international scienti
fi
c
and practical conference of young
scientists]. Karavayevo: Kostroma
State Agricultural Academy, 2016,
pp. 120–123.
5. Losev S.B.
Ob ispol'zovanii faznyh
koordinat pri raschete slozhnone-
simmetrichnyh rezhimov
[On the use
of phase coordinates in the calcula-
tion of complex asymmetric modes]
//
Elektrichestvo
[Electricity], 1979,
no 1, pp. 15–23.
6. Zavarygin V.M.
Chislennye metody
[Numerical methods]. M.: Education,
1991, 250 p.
Оригинал статьи: Эмпирические критерии для определения места повреждения в электрических сетях 6 кВ
Исследована возможность определения места повреждения в сетях 6 кВ по эмпирическим критериям для разных видов аварийных режимов. При разработке критериев использованы модули фазных напряжений и токов в начале линии 6 кВ. Для всех разработанных эмпирических критериев получены их интерполяционные зависимости от точки повреждения вдоль длины линии. Показано, что погрешность определения места повреждения для всех аварийных режимов не превышает 7%, за исключением режима обрыва фазы.