Электростатические и электродинамические силы в КРУЭ при нормальном режиме работы

Page 1

Page 2

106

оборудование

Электростатические
и электродинамические силы
в КРУЭ при нормальном
режиме работы

УДК 621.316.37

Ярмаркин

к.т.н., доцент,

заведующий кафедрой

ЭЭСП ФГАОУ ДПО

«Петербургский

энергетический

институт повышения

квалификации»

Дубицкий

к.т.н., ассистент Высшей

школы высоковольтной

энергетики Санкт-

Петербургского

политехнического

университета Петра

Великого

статье

рассмотрены

силы

электростатического

взаимодействия

возникаю

щие

между

токоведущими

проводниками

оболочкой

трехфазных

сборных

шинах

КРУЭ

либо

трехфазных

газоизолированных

линиях

электропередачи

Получена

формула

силы

Кулона

между

параллельными

проводниками

Показа

но

что

сила

Кулона

меняется

частотой

100

Гц

имеет

постоянную

составляю

щую

достигает

системах

класса

напряжения

110–500

кВ

может

быть

причиной

резонансных

вибраций

Теоретические

выводы

проверены

конечно

элементным

моделированием

электростатического

поля

Ключевые

слова

сила Кулона,

вибрация, сборные

шины, КРУЭ, метод

конечных элементов,

электростатика, тензор

Максвелла

ри нормальной работе КРУЭ на высоковольтных элементах

присутствует рабочее (фазное) напряжение и возникают за-

ряды. Взаимодействие между зарядами, распределенными

на различных фазах, а также на оболочке, приводит к воз-

никновению сил Кулона, или электростатических сил. Известно, что

эти силы значительно меньше сил Ампера (сил электродинамического

взаимодействия), возникающих при протекании токов короткого замы-

кания. При статическом нагружении силы Кулона не создают в эле-

ментах конструкции опасных напряжений и не приводят к аварийным

ситуациям. По этим причинам, как правило, при проектировании КРУЭ

силы Кулона не принимают во внимание, ограничиваясь при механи-

ческих расчетах анализом сил Ампера.

Между тем, как показывают выполненные ниже расчеты, силы

Кулона могут достигать заметной величины. Кроме того, как и силы

электродинамического взаимодействия, силы Кулона меняются во

времени с удвоенной частотой приложенного напряжения (100 Гц).

Это обстоятельство может приводить к вибрациям токоведущей си-

стемы. В случае, если собственная частота колебаний токоведущих

элементов оказывается близка или кратна частоте воздействующей

силы, возможно возникновение резонанса. При длительной работе

КРУЭ резонансные колебания способны создавать усталостные раз-

рушения в контактных элементах токоведущей системы, в самих этих

элементах, а также в элементах опорной изоляции.

Следует ожидать что возникновение вибраций под действием сил

Кулона наиболее вероятно в системе трехфазных сборных шин (СШ),

либо в трехфазной газоизолированной линии электропередачи (ГИЛ),

когда взаимное влияние протяженных проводников относительно ве-

лико, а собственная частота колебаний этих проводников относитель-

но мала и близка к 100 Гц.

СИЛА

КУЛОНА

СИСТЕМЕ

ПАРАЛЛЕЛЬНЫХ

ПРОВОДНИКОВ

Очевидно, что при концентрическом расположении токоведущей

шины внутри цилиндрической оболочки возникающие силы Кулона не

создают никакого усилия, направленного на перемещение или изгиб

токоведущей шины. Напротив, при наличии нескольких токоведущих

Page 3

107

шин внутри общей оболочки взаимодействие между

зарядами на соседних шинах и оболочке вполне спо-

собно создавать такие усилия. Для оценки возника-

ющих сил Кулона определим силу взаимодействия

между двумя параллельными протяженными прово-

дниками в предположении, что заряды проводников

сосредоточены на их оси.

Можно показать, что если мгновенные значения

плотности зарядов на соседних фазах в зависимости

от времени

определяются формулами:



max

sin

(



) и



max

sin

(



–



) ,

то сила взаимодействия между ними равна:



max



max

(

) = — — [

cos



–

cos



–



)],

(1)



где

— расстояние между проводниками,



– диэлек-

трическая проницаемость.

Это означает, что результирующая сила изменя-

ется с удвоенной частотой 2



, а также имеет посто-

янную составляющую.

Выполненные оценки при характерных для КРУЭ

220 кВ размерах показывают, что при наличии рабо-

чего напряжения и при отсутствии нагрузки между

проводниками соседних фаз действует сила Кулона,

по порядку величины близкая к 3 Н/м и изменяющая-

ся во времени с частотой 100 Гц.

Как в двухфазной системе с противоположными

потенциалами, так и в трехфазной системе шин сила

Кулона, действующая между проводниками, всег-

да стремится прижать их друг к другу, переместить

проводники к центру системы. При наличии общей

оболочки между каждым из фазных проводников

и оболочкой возникают силы, стремящиеся притя-

нуть проводники к оболочке, то есть направленные

от центра. В результате их общего действия, при

наличии общей оболочки, суммарная сила Кулона

существенно изменяется. Покажем это на примере

системы сборных шин КРУЭ 220 кВ.

СИЛА

КУЛОНА

ТРЕХФАЗНОМ

ТОКОПРОВОДЕ

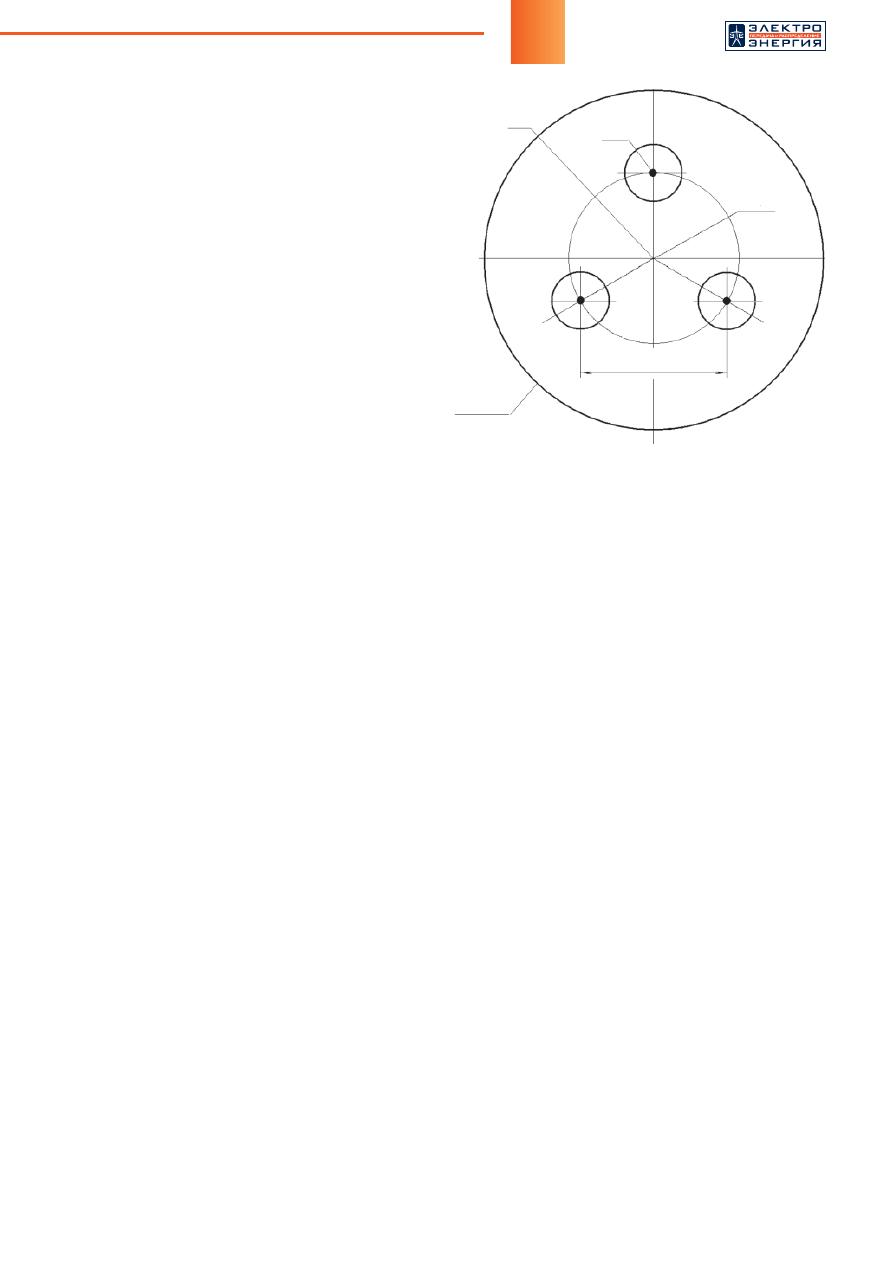
Будем анализировать силу Кулона в системе трех-

фазного токопровода (рисунок 1) при заземленной

оболочке и заданных потенциалах на фазных про-

водниках:

max

sin

(



max

sin

(



– 120°),

max

sin

(



– 240°).

Формула (1) дает принципиальную возможность

расчета сил Кулона и в трехфазной системе сборных

шин или токоведущих проводников ГИЛ. Методика

вычисления зарядов в такой системе описана в [1].

Используя подход, описанный выше применительно

к двухфазной системе, можно показать, что в трех-

фазной системе сборных шин силы Кулона сохраня-

ют отмеченные выше свойства:

1) наличие составляющей, меняющейся с частотой

100 Гц;

2) наличие постоянной составляющей.

Кроме того, легко показать, что при симметричной

системе приложенных напряжений и при симметрич-

ном расположении шин относительно оси оболочки

силы электростатического взаимодействия между

шинами всегда стремятся притянуть шины одна

к другой, в то время как силы взаимодействия между

каждой шиной и заземленной оболочкой всегда на-

правлены в противоположную сторону, то есть стре-

мятся притянуть каждую шину к оболочке и развести

шины одна от другой.

Более эффективно и целесообразно, однако, вы-

полнить анализ сил Кулона с учетом точной геоме-

трии трехфазного токопровода, используя численные

методы и существующие программные продукты.

В настоящей работе анализ двумерного электроста-

тического поля выполнен методом конечных элемен-

тов с использованием программы ELCUT [2, 3] при-

менительно к симметричной системе трех фазных

проводников, расположенных внутри общей цилин-

дрической оболочки, как показано на рисунке 1.

Граничные условия для данной задачи представ-

ляют собой заданные мгновенные значения потен-

циала на наружных поверхностях фазных проводни-

ков и нулевой потенциал внутренней поверхности

оболочки. Поскольку потенциалы фаз меняются во

времени по синусоидальному закону, задача реша-

лась многократно для разных значений фазного угла



от 0 до 360° с шагом 5°.

Следует заметить, что на рисунке 1 показана

симметричная конструкция, в которой центры токо-

ведущих шин образуют правильный треугольник.

При проектировании СШ, как правило, две шины из

трех разведены на большее расстояние для вывода

между ними третьей фазы. Центры сечений при этом

образуют равнобедренный, но не равносторонний

треугольник. Это обстоятельство не меняет основ-

ных сделанных ниже выводов.

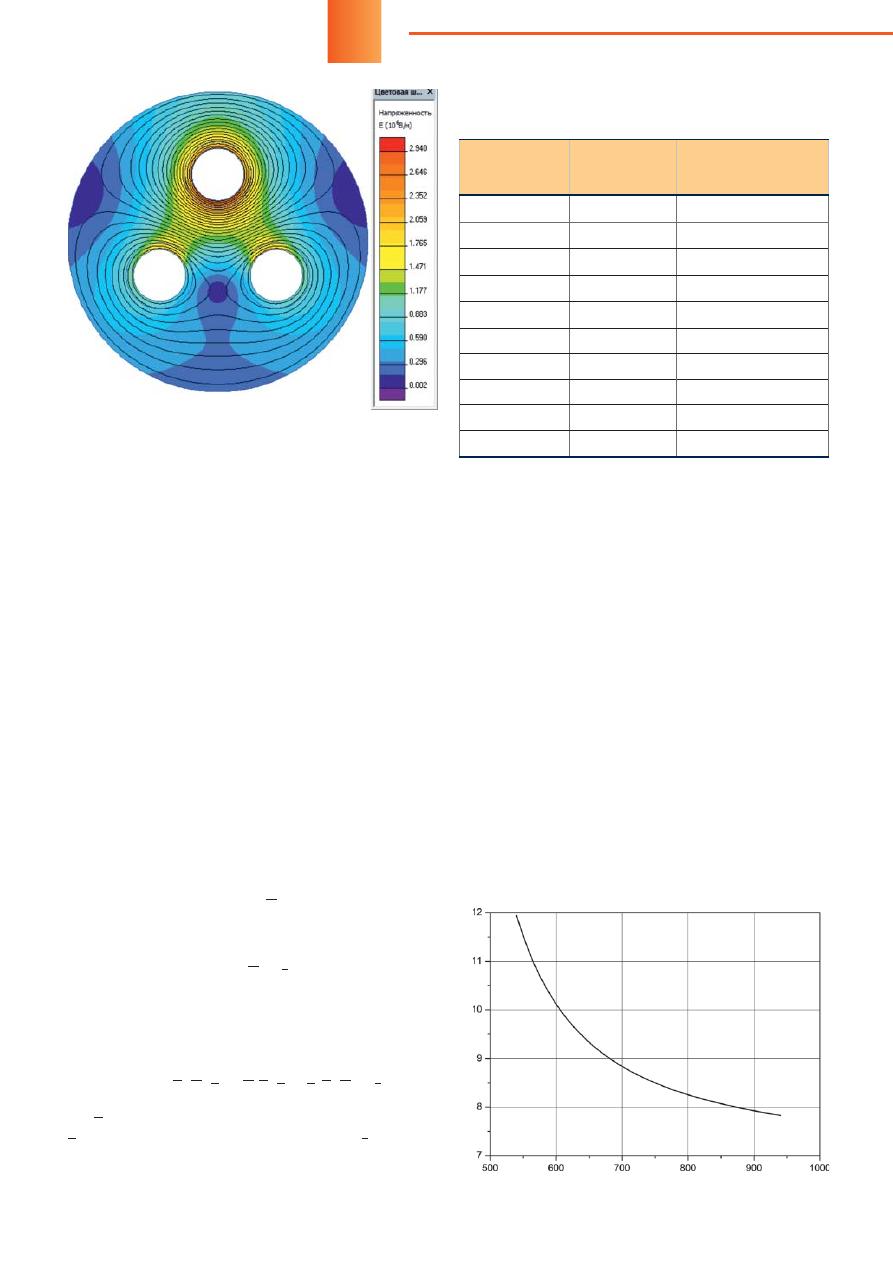
На рисунке 2 показана расчетная модель и кар-

тина распределения напряженности на поверхности

проводящих элементов в момент времени, когда на

верхнем фазном проводнике потенциал достиг ам-

плитудного значения.

Рис

. 1.

Трехфазная

симметричная

система

сборных

шин

= 0



№

5 (62) 2020

Page 4

108

Для расчета использованы следующие параме-

тры расчетной модели:

– радиус токоведущей шины 62,5 мм;

– расстояние между осями фазных проводников

280 мм;

– действующее значение потенциала на фазных

проводниках 127 кВ.

В приведенных ниже расчетах радиус оболочки

изменялся в пределах от 275 мм до 470 мм.

Поскольку плотность зарядов на поверхности

проводников пропорциональна напряженности, ри-

сунок 2 дает представление о зарядах как источни-

ках сил Кулона. Видно, например, что на верхней

фазе распределение заряда по окружности цилин-

дра близко к равномерному.

Результаты выполненного расчета сведены в та-

блицу 1 и показаны графиками рисунков 3–5.

В таблице 1 приведены величины зарядов (ам-

плитудные значения, Кл/м) на проводниках и сил

(значения при



= 90°, Н/м), действующих на прово-

дники, в зависимости от диаметра

об

= 2

Заряд фазного проводника вычислялся по тео-

реме Гаусса путем интегрирования потока вектора

электрического смещения

через замкнутую по-

верхность

, целиком охватывающую фазный про-

водник:

∫°

Механическая сила

, действующая со стороны

электрического поля на фазный проводник, вычисля-

ется как поток тензора тяжения Максвелла через ту

же поверхность:

= —

∫°

(

) +

(

) +

(

)

где

— вектор напряженности электрического поля;

— вектор нормали к малому элементу

Видно, например, что при

= 360 мм вычислен-

ное амплитудное значение заряда на проводнике

№ 1 (А) равно



max

= 8,69 мкКл/м. Это на 30% больше

величины 6,65 мкКл/м, полученной для двухфазной

системы с такими же размерами, но без оболочки.

Различие указывает на существенное влияние как

соседних проводников, так и заземленной оболоч-

ки.

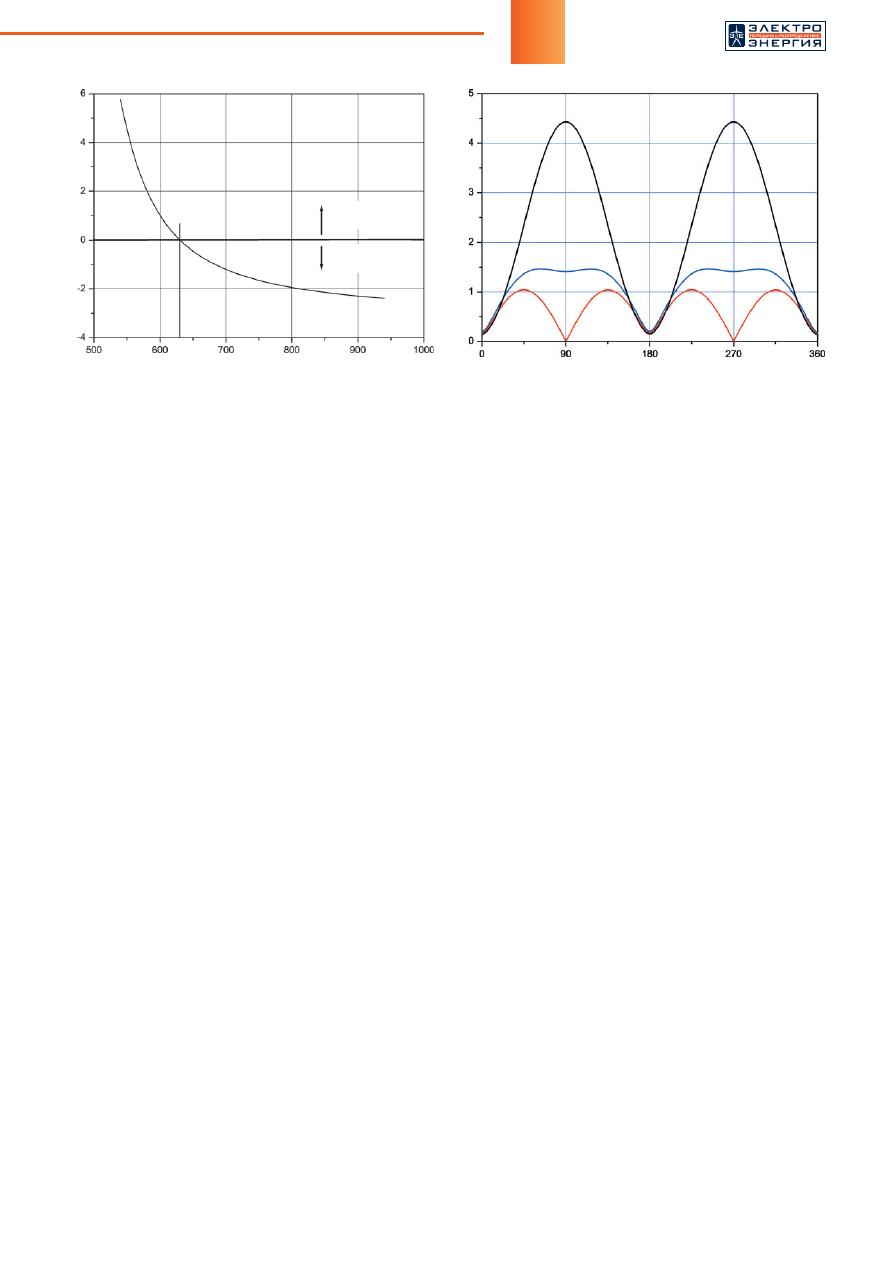
На рисунке 3 показана зависимость заряда на

проводнике № 1 от диаметра оболочки

об

. При

уменьшении диаметра заряд неограниченно воз-

растает, что связано с приближением стенки обо-

лочки к фазному проводнику. При неограниченном

увеличении диаметра

об

заряд стремится к пре-

дельному значению, характеризующему трехфаз-

ную систему проводников при отсутствии оболочки.

Видно, что преобладающее влияние на формиро-

вание силы Кулона оказывает либо оболочка, либо

соседние проводники в зависимости от размеров

оболочки и токоведущей системы.

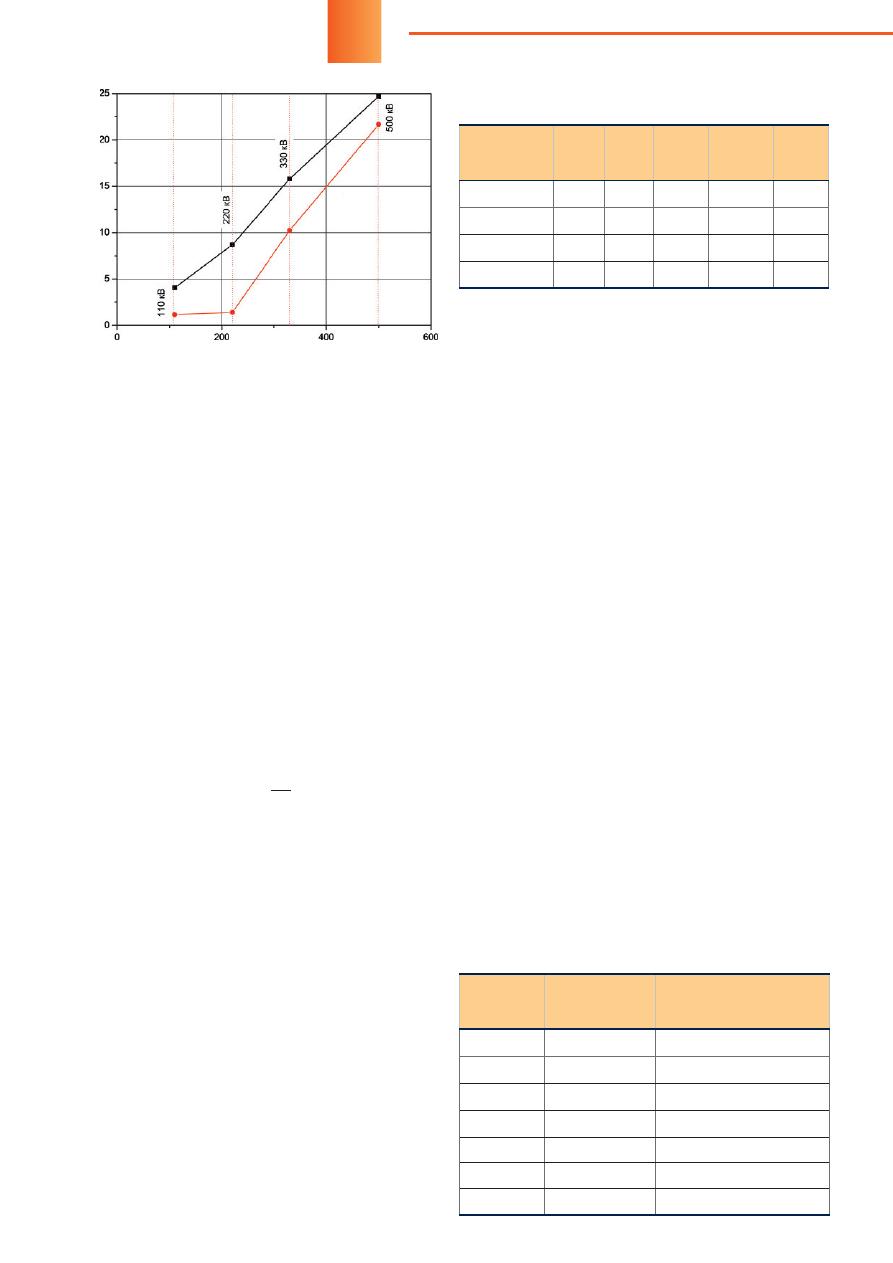
Это хорошо видно также на рисунке 4, где по-

казана зависимость силы, действующей на прово-

дник, от диаметра

об

при фазном угле



= 90°, то

есть в момент времени, когда заряд на проводнике

достигает амплитудного значения. В этот момент

сила, действующая на проводник, также близка

к максимуму. Ввиду симметрии геометрического

Рис

. 2.

Картина

распределения

напряженности

электри

ческого

поля

трехфазном

токопроводе

220

кВ

(

расчет

ная

модель

по

рисунку

Табл. 1. Показатели величины

зарядов на проводниках и сил, действующих

на проводники, в зависимости от диаметра

Диаметр

оболочки 2

мм

Заряд (ампл.),

мкКл/м

Сила Кулона

при



= 90°, Н/м

550

11,5

4,44

572

10,77

2,49

604

10,03

0,82

630

9,60

0,00

668

9,13

–0,77

700

8,84

–1,20

720

8,69

–1,41

780

8,34

–1,84

860

8,04

–2,18

940

7,83

–2,38

Рис

. 3.

Изменение

заряда

зависимости

от

диаметра

оболочки

Диаметр оболочки, мм

Зар

яд, мкКл/м

ОБОРУДОВАНИЕ

Page 5

109

строения сис темы и симметричной системы заря-

дов, в этот момент сила Кулона направлена точно

вдоль радиуса оболочки. Она может быть направ-

лена к центру системы (отрицательные значения),

или в сторону оболочки (положительные значения).

Можно заметить, что существует такой диаметр

об

, при котором наступает равновесие между

силой, действующей со стороны оболочки, и си-

лами, действующими со стороны соседних про-

водников. Это происходит при диаметре оболоч-

ки, близком к

об

= 2

= 630 мм, когда суммарная

сила близка к нулю в момент максимума заряда



= 90°.

Следует подчеркнуть, что возникающие силы

незначительны по отношению к механической проч-

ности элементов токопровода при статическом при-

ложении, однако могут быть источником вибраций,

в особенности в условиях резонанса с собственны-

ми частотами колебаний токоведущих шин.

На рисунке 5 показана зависимость от времени

силы Кулона, действующей на фазный проводник

в системе рисунков 1 и 2 в пределах периода часто-

ты 50 Гц при различных размерах оболочки. Ампли-

тудное значение заряда достигается в момент вре-

мени, когда потенциал и заряд фазного проводника

достигают максимального значения при фазовом

угле, равном 90°, либо 270°. Как видно из формулы

(1) и рисунка 5, сила Кулона меняется во времени

существенно различным образом в зависимости от

размеров оболочки.

Например, при

об

= 720 мм (кривая 1 рисунка 5)

амплитудное значение силы равно

max

= 1,47 Н/м.

Это значение значительно (почти вдвое) меньше,

чем сила, действующая в двухфазной системе с со-

впадающими геометрическими размерами, но при

отсутствии оболочки. Действие соседних прово-

дников и оболочки уравновешивается, что приво-

дит к уменьшению суммарной величины. Отметим,

что амплитудное значение силы (1,47 Н/м) достига-

ется при фазном угле



= 60°, в то время как при



= 90° сила меньше (1,41 Н/м). При этом верти-

кальная составляющая силы всегда направлена

к оси оболочки, то есть в терминах рисунка 4 сила

отрицательна.

Интересно проследить за изменением силы при

об

= 630 мм. Как видно из рисунков 4 и 5, в момент



= 90°, при амплитудном значении заряда, на фаз-

ный проводник действует нулевая суммарная сила.

При этом, однако, она достигает заметного значе-

ния (1,04 Н/м) при фазном угле



= 45°. Вертикаль-

ная составляющая силы также всегда направлена

к оси оболочки. Основной вклад в модуль силы

дает, однако, горизонтальная составляющая, кото-

рая дважды меняет знак в пределах периода 50 Гц.

При малом диаметре оболочки при

об

= 630 мм

(кривая 3 рисунка 5) вертикальная составляющая

силы направлена в сторону оболочки (вверх на ри-

сунке 1) за исключением малых интервалов времени

вблизи моментов перехода заряда через ноль.

Можно отметить, что при нулевом заряде на фаз-

ном проводнике сила Кулона не обращается в ноль

из-за разделения зарядов, индуцированных со сто-

роны соседних фаз.

СИЛЫ

КУЛОНА

КРУЭ

РАЗЛИЧНЫХ

КЛАССОВ

НАПРЯЖЕНИЯ

Представляет интерес проследить, как меняются

силы Кулона в зависимости от класса напряжения.

Для этого была использована однотипная расчетная

модель, показанная на рисунке 1. Расчетная система

представляет собой симметрично расположенные

три фазных проводника в общей заземленной обо-

лочке радиуса

. Фазные проводники расположены

на окружности с радиусом

, радиус сечения прово-

дника обозначен

В таблице 2 для классов напряжения 110–330 кВ

приведены параметры расчетной модели, исполь-

зуемые при практическом изготовлении КРУЭ. Ис-

ключение составляют оценочные размеры в классе

500 кВ, для которого практическая реализация по-

добной системы авторам неизвестна. Данные табли-

цы 2 показаны графиками рисунка 6.

Видно, что при переходе от класса напряжения

220 кВ к классу 330 кВ и далее к классу 500 кВ заряд

на фазном проводнике и действующая на него сила

Кулона быстро возрастают, достигая 24,7 мкКл/м

и 21,7 Н/м в классе 500 кВ. Это прямо указывает на

Рис

. 4.

Сила

действующая

на

токоведущий

проводник

при



= 90°,

зависимости

от

диаметра

оболочки

об

Рис

. 5.

Изменение

модуля

силы

зависимости

от

вре

мени

(

по

горизонтальной

оси

отложен

фазовый

угол

приложенного

напряжения

Гц

): 1 —

об

= 550

мм

;

2 —

об

= 630

мм

; 3 —

об

= 720

мм

Сила направлена

к стенке оболочки

Сила направлена

к оси оболочки

Диаметр оболочки, мм

Фаза, град.

Сила Ку

лона, Н/м

Сила Ку

лона, Н/м

№

5 (62) 2020

Page 6

110

возрастающую опасность возникновения вибрации

и усталостного разрушения элементов трехфазных

сборных шин либо ГИЛ.

ОЦЕНКА

МЕХАНИЧЕСКИХ

СВОЙСТВ

ПРОВОДНИКОВ

СБОРНЫХ

ШИН

ГИЛ

Определенные выше силы Кулона, как и силы элек-

тродинамического взаимодействия, приложены

к элементам элегазового токопровода в поперечном

направлении, вызывая изгиб либо вибрацию. При

этом проводящие шины токопровода, как правило,

представляют собой балку, жестко фиксированную

с двух сторон опорными изоляторами. Длина про-

водника между опорами

, а также геометрическая

форма и размеры сечения балки определяют ее ви-

брационные свойства, в том числе собственные ча-

стоты колебаний. Расчет резонансных частот балки,

закрепленной на двух концах, выполняется на осно-

ве известной формулы теоретической механики:



E J



= —

√

— ,

(2)



где

= 1, 2, 3… — номер гармоники;



— круговая

частота колебаний, рад/с;

— длина балки между

опорами, м;

— модуль упругости материала балки,

МПа;

— осевой момент инерции, м

;



— плотность

материала, кг/м

; П — площадь поперечного сечения

балки, м

В качестве исходных данных для расчета при-

нято, что токоведущая шина изготовлена из алю-

миниевой трубы с внешним диаметром

= 125 мм,

внутренним диаметром

= 95 мм. Это позволяет

принять следующие численные значения параме-

тров



– плотность алюминия



= 2700 кг/м

;

– модуль упругости алюминия

= 70 000 МПа.

После подстановки принятых значений

по-

лучаем П

= 5,183 ∙ 10

-3

Для определения осевого момента инерции тру-

бы используем известную формулу:



(1 –

) / 64.

После постановки параметров

получаем

= 8∙10

-6

В дальнейшем для определения собственной ча-

стоты колебаний балки по формуле (2) использовано

значение

= 1, то есть определяется только основная

(она же минимальная) частота собственных колеба-

ний



. В таблице 3 приведены значения основной

частоты собственных колебаний в зависимости от

длины балки (расстояния между опорными изолято-

рами в токопроводе).

Как видно из таблицы 3, при длине балки между

опорами

= 2 м частота собственных колебаний

равна 78,5 Гц, то есть меньше 100 Гц. Учитывая ре-

зультаты, полученные относительно воздействую-

щей силы, следует отметить, что при длине балки,

близкой к 1,5–2 м, частота собственных колебаний

практически совпадает с частотой воздействующей

силы 100 Гц, то есть возникают условия резонанса.

При конструировании ГИЛ с большими расстояния-

ми между точками опоры можно предположить воз-

никновение еще более благоприятных условий для

резонансных вибраций.

СИЛЫ

КУЛОНА

СИЛЫ

АМПЕРА

В заключение можно отметить, что при наличии на-

грузки и протекании рабочего тока по проводникам

трехфазной системы одновременно с силами Куло-

на возникают также электродинамические силы, или

силы Ампера. При рабочем токе силы Кулона и силы

Ампера сопоставимы по величине. В качестве приме-

ра вычислим силу Ампера, действующую между ли-

нейными протяженными проводниками, находящими-

ся на расстоянии

= 280 мм, как в системе рисунка 2.

Воспользуемся для этого известной формулой:





(3)

Табл. 2. Параметры расчетной модели

для классов напряжения 110–330 кВ

Класс

напряжения,

кВ

мм

, мм



max

мкКл/м

max

Н/м

110

275

37,5

160

4,06

1,17

220

360

62,5

180

8,69

1,41

330

600

100

330

15,8

10,23

500

750

125

400

24,7

21,67

Табл. 3. Значения основной частоты собственных

колебаний в зависимости от длины балки

Длина

балки

Резонансная

частота балки



, рад/с

Основная частота

собственных колебаний





, Гц

1972

313,85

493

78,46

219,3

34,90

123

19,57

4,5

97,5

15,51

78,95

12,56

54,8

8,72

Рис

. 6.

Параметры

трехфазных

токопроводов

ГИЛ

раз

личных

классов

напряжения

(

по

таблице

2): 1 —

амплиту

да

заряда

(

мкКл

); 2 —

максимум

силы

Кулона

(

)

Номинальное напряжение (класс напряжения), кВ

Амплит

уда з

ар

яда, мкКл/м

ак

сим

альная сила , Н/м

ОБОРУДОВАНИЕ

Page 7

111

где

— токи в проводниках;

— расстояние меж-

ду проводниками;



— магнитная постоянная.

При

= √2 ∙ 630 = 891 А вычисления по фор-

муле (3) дают величину силы 0,567 Н, то есть по по-

рядку величины сила Ампера в этом случае близка

к силе Кулона. Совершенно ясно, что при изменении

тока соотношение этих сил может существенно из-

меняться.

Силы Ампера, как и силы Кулона, в трехфазной

системе проводников имеют постоянную составляю-

щую, а также составляющую с частотой 100 Гц, об-

условленную взаимодействием фазных проводников

между собой и с оболочкой. При этом электродина-

мические силы расталкивают проводники, в то время

как электростатические силы могут быть направлены

к оси оболочки, либо в сторону стенки, как показано

на рисунке 5. В зависимости от нагрузки, могут преоб-

ладать силы Кулона либо силы Ампера. В результате

этого по мере увеличения нагрузки вибрация прово-

дников может исчезнуть и вновь появиться. Кроме

того, влияние на это явление оказывает характер на-

грузки, проявляющийся в изменении фазных углов

протекающих токов. Все эти обстоятельства целесо-

образно принимать во внимание при проектировании

КРУЭ и, в особенности, ГИЛ в общей оболочке.

ВЫВОДЫ

1. При размерах системы трехфазных проводников,

характерных для КРУЭ классов 110–330 кВ, действу-

ющие на фазные проводники силы Кулона достигают

10 Н/м при рабочем напряжении независимо от на-

грузки.

2. Силы Кулона в трехфазной системе проводников

имеют постоянную составляющую, а также составля-

ющую с частотой 100 Гц, обусловленную взаимодей-

ствием фазных проводников между собой и с обо-

лочкой.

3. При размерах сборных шин, характерных для

КРУЭ, резонансные частоты проводников близки

к 100 Гц. Это может быть причиной резонансных ко-

лебаний под действием сил Кулона и должно быть

учтено при проектировании КРУЭ и ГИЛ.

ЛИТЕРАТУРА
1. Теория электрических аппаратов. Под ред. проф.

Г.Н. Александрова. М.: Высш. шк., 1985. 312 с.

2. ELCUT 6.4. Руководство пользователя. URL: http://elcut.

ru/free_doc_r.htm.

3. Дубицкий С.Д. Инженерное моде лирование квазиста-

тического электромагнитного поля в программе ELCUT

для задач электроники // Силовая электроника — тема-

тическое приложение к журналу «Компоненты и техно-

логии», 2017, № 6. С. 64–68.

REFERENCES
1. Theory of electrical apparatuses. Edited by professor Alek-

sandrova G.N. Moscow, Higher school Publ., 1985. 312 p.

(In Russian)

2. ELCUT 6.4 User manual. URL: http://elcut.ru/free_doc_r.htm.
3. Dubitskiy S.D. Engineering simulation of quasi-static elec-

tromagnetic ﬁ eld in ELCUT program for electronics pur-

poses // Power Electronics - specialist supplement to the

magazine "Components and Technologies", 2017, no. 6,

pp. 64–68. (In Russian)

Ïðåîáðàçîâàòåëè
èçìåðèòåëüíûå
íàïðÿæåíèÿ ÏÈÍ
îò 50 Â äî 3000 Â

Âûñîêîâîëüòíûå

ýëåêòðîííûå

êëåùè ÊÒ-1000-Â

äëÿ èçìåðåíèÿ òîêà

äî 1000 À ïðè

íàïðÿæåíèè íà

òîêîâîé øèíå

äî 10 000 Â

Ïðåîáðàçîâàòåëè èçìåðèòåëüíûå

ìîùíîñòè ñåðèè ÏÈÌ

äëÿ êîíòðîëÿ àêòèâíîé ìîùíîñòè

â äèàïàçîíå îò 1 äî 4000 êÂò

Ïðåîáðàçîâàòåëè èçìåðèòåëüíûå

òîêà ñåðèè ÏÈÒ äëÿ èçìåðåíèÿ òîêà

îò 40 ìÀ äî 25 000 À

Преобразователи

(

датчики

)

для

энергетиков

от

ООО

НПО

Горизонт

Плюс

C=…,

nnn

&mon

&c%!,ƒ%…2

ãĊ

“[

(

h“2!=

l%“*%"“*%L

Ëąã

C!,K%!/

“%K“2"

……%L

!=ƒ!=K%2*,

ąã

,ƒ

äË

…,

2%*=

…=C! ›

…,

=*2,"…%L

%?…%“2,.

%K!=ƒ%"=2

Ëã

“

!2,-,

,!%"=…/

"…

“

…/

c%“!

ËË

“2!

Ëą

“2="

%“2%L…3

ƒ=

äË

…3

C%!2…/

=…=

“%%2…%

ĈË

…,

ĆË

…=

ćË

“2"%.

C=…,

nnn

&mon

&c%!,ƒ%…2

ãĊ

“[

%“3?

“2"

“C

=2…3

%“2="*3

%K!=ƒ%"=2

ËãË

"“

ËĄ

,%…/

“2!=…/

qmc

www.g

riz

ont-pl

us.ru

%K!=ƒ%"=2

Ëã

(

,*,)

“C

Ëć

,"=

ãĉ

"=…,

ćË

“*3

,ƒ%

…/

ĆË

%K…/L

…%L

,…2

L“

(4$

www.g

riz

ont-pl

us.ru

На прав

ах рек

ламы

№

5 (62) 2020

Оригинал статьи: Электростатические и электродинамические силы в КРУЭ при нормальном режиме работы

Ключевые слова: сила Кулона, вибрация, сборные шины, КРУЭ, метод конечных элементов, электростатика, тензор Максвелла

Читать онлайн

В статье рассмотрены силы электростатического взаимодействия, возникающие между токоведущими проводниками и оболочкой в трехфазных сборных шинах КРУЭ, либо в трехфазных газоизолированных линиях электропередачи. Получена формула силы Кулона между параллельными проводниками. Показано, что сила Кулона меняется с частотой 100 Гц, имеет постоянную составляющую, достигает 20 Н/м в системах класса напряжения 110–500 кВ и может быть причиной резонансных вибраций. Теоретические выводы проверены конечно-элементным моделированием электростатического поля.