«КАБЕЛЬ-news», № 3, 2013, www.kabel-news.ru
32
Актуально
ÊÀÁÅËÜÍÛÅ ËÈÍÈÈ
ВВЕДЕНИЕ
На протяжении нескольких десятилетий, в том
числе и в последнее время, публикуются работы [1,
2], демонстрирующие применение метода конечных
элементов для расчёта температурного поля кабель-
ной линии. В простейшем случае рассчитывается
температурное поле при заданной плотности оми-
ческих потерь без учёта токов в экранах [3, 4]. В [5]
учёт потерь в экране и броне проводится при помо-
щи специализированной программы «Экран» [6].
В [7] проводится совместное решение уравнений
электро магнитного поля и тепло про водности, однако
отсутствие присо единённой электри ческой цепи за-
ставляет исполь зовать упрощённые условия зазем-
ления и не позволяет оценивать потери при одновре-
менном использовании экрана и брони. Применение
современных программ расчёта электромагнитных и
тепловых полей методом конечных элементов даёт
возможность учесть максимальное число факторов,
ограничивающих нагрузочную способность кабелей,
без дополнительных упрощающих предположений, а
именно:
• позволяет анализировать как устано
вившееся,
так и переходное тепловое поле в режи ме симме-
тричной нагрузки и в любых видах коротких за-
мыканий и иных аномальных режимах;
• снимает ограничения на моделирование реаль-
ных условий прокладки кабельных групп — в зем-
ле, на воздухе, в лотках и каналах, с применени-
ем засыпки и т.п.;
• даёт возможность включать в модель несколь-
ко параллель ных кабельных линий с учётом их
электромаг нитного и теплового влияния друг на
друга;
• одновременное получение данных о величине
внешнего магнитного поля, которое нормирует-
ся с точки зрения электромагнитной экологии,
что позволяет деталь
но учесть эффективность
принятых мер по экрани рованию конструк ции ка-
бельной линии.
Расчет состоит из следующих этапов.
МЕТОДИКА РАСЧЁТА
Решение уравнений электромагнитного поля для
определения джоулевых потерь в экранах и бро-
не. Уравнения квазистационарного переменного
магнитного поля в частотной области с вихревыми
токами записываются относительно комплексного
векторного магнитного потенциала, который в дву-
мерном плоскопараллельном приближении имеет
только одну ненулевую компоненту A = A
z
:
,
(1)
где:
μ — магнитная проницаемость, Гн/м,
Численный метод анализа
нагрузочной способности
высоковольтной кабельной
системы
В данной статье представлена методика совместного расчёта электро-
магнитного и температурного полей трёхфазной кабельной линии с изоляци-
ей из сшитого полиэтилена при однофазной прокладке.
Георгий ГРЕШНЯКОВ, заведующий лабораторией, к.т.н.,
Геннадий КОВАЛЁВ, директор, к.ф-м.н., НИИ «Севкабель»,
Семён ДУБИЦКИЙ, директор ООО «ТОР»
«КАБЕЛЬ-news», № 3, 2013, www.kabel-news.ru
33
Актуально
ÊÀÁÅËÜÍÛÅ ËÈÍÈÈ
γ
— удельная электропроводность, См/м,
ω
— циклическая частота, рад/с,
j
cтор
— плотность стороннего тока, А/м
2
.
При расчёте электромагнитного поля двумерная
расчётная область представляет собой поперечные
сечения всех трёх кабелей, погружённых в грунт
на проектную глубину. Электропроводность грунта
также учтена, равно как возможные металлические
конструкции (лотки, трубопроводы, арматура), нахо-
дящиеся вблизи кабельной линии.
Необходимость учёта схемы соединения экранов
(одностороннего, двустороннего заземления или с
транспозицией) требует совместного решения урав-
нения магнитного поля (1) с уравнениями присоеди-
нённой электрической цепи. Уравнение ветви, со-
держащей массивный проводник в магнитном поле,
имеет вид:
,
(2)
где:
U — разность потенциалов на концах проводника, В,
R — активное сопротивление проводника на посто-
янном токе, Ом,
A — векторный магнитный потенциал, В б/м.
Интегрирование выполняется по площади попе-
речного сечения проводника
Ώ
.
Результатом совместного численного решения
уравнений (1 и 2) является распределение плотно-
сти тока в проводящих элементах системы (жиле,
экране и броне кабеля, прилегающих металлокон-
струкциях). Расчёт может проводиться как при но-
минальной симметричной токовой нагрузке линии,
так и в аварийных, в том числе несимметричных
режимах.
Основным результатом расчёта в нашем случае
является распределение мощности омического те-
пловыделения, которое передаётся в качестве ис-
точника тепла в следующий этап решения. Отметим
также, что в результате электромагнитного расчёта
мы получаем распределение магнитного поля на по-
верхности земли и над нею, что может быть полезно
для оценки условий электромагнитной экологии.
На втором этапе в той же расчётной области на
той же самой сетке конечных элементов решается
уравнение теплопроводности:
,
(3)
где:
T — температура, К,
t — время, с,
λ
— теплопроводность, Вт/(м·К),
q — плотность мощности источника тепла, Вт/м
3
,
с — удельная теплоёмкость, Дж/(кг·К),
ρ
— плотность, кг/м
3
.
Решение уравнения (3) осуществляется с гранич-
ными условиями, которые могут моделировать кон-
векцию при заданной скорости обдува, солнечную
радиацию и другие условия прокладки. Естествен-
ным образом учитывается различная теплопровод-
ность грунта. Имеется также возможность учёта
изменения теплопроводности грунта из-за его высы-
хания путём организации итерационного процесса.
ЭЛЕКТРОМАГНИТНЫЙ РАСЧЁТ
Рассмотрим одноцепную трёхфазную кабельную
линию, собранную из трёх однофазных кабелей на-
пряжением 35 кВ, при различных способах объеди-
нения однофазных кабелей в трёхфазную группу:
треугольником встык, линейно с зазором, равным
диаметру кабеля. В данной статье анализируется
подземное расположение кабелей с засыпкой грун-
том, однако методика пригодна и для других условий
прокладки, в том числе в кабельных лотках, в воз-
духе и т.п.
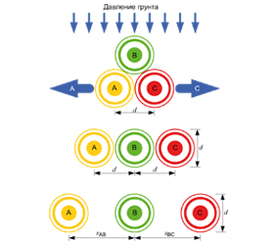
Кабели расположены треугольником
На рис.1 представлен эскиз поперечного сечения
кабельной линии, а в табл. 1 — основные характери-
стические параметры прокладываемого кабеля.
Рис. 1. Эскиз поперечного сечения кабельной линии
Зададимся длиной линии L
К
= 1 км.
Задача состоит в вычислении наведённых то-
ков в экранах и броне и потерь от них. Допускаются
симметричный характер нагрузки и симметричная
система токов жил с действующим значением тока
I
фазы 700 А. Предположение симметрии токов жил
является упрощающим допущением, поскольку вви-
«КАБЕЛЬ-news», № 3, 2013, www.kabel-news.ru
34
Актуально
ÊÀÁÅËÜÍÛÅ ËÈÍÈÈ
ду особенностей расположения кабелей магнитные
условия взаимодействия разных фаз слегка различ-
ны. Однако это предположение является обычным
для практики расчётов. Важно отметить, что относи-
тельно экранов и брони никаких допущений о сим-
метрии токов не делается.
Одностороннее заземление экрана.
Рассмо-
трим линию, в которой заземление экрана выполне-
но с одной стороны, но каждый кабель поверх экра-
на имеет алюминиевую броню, которая соединяется
с экраном на обоих концах кабеля. Схема электри-
ческих соединений моделируется присоединённой
к исходной задаче электрической цепью, программ-
ный пакет ELCUT [8] позволяет решать связанные
цепные и полевые задачи.
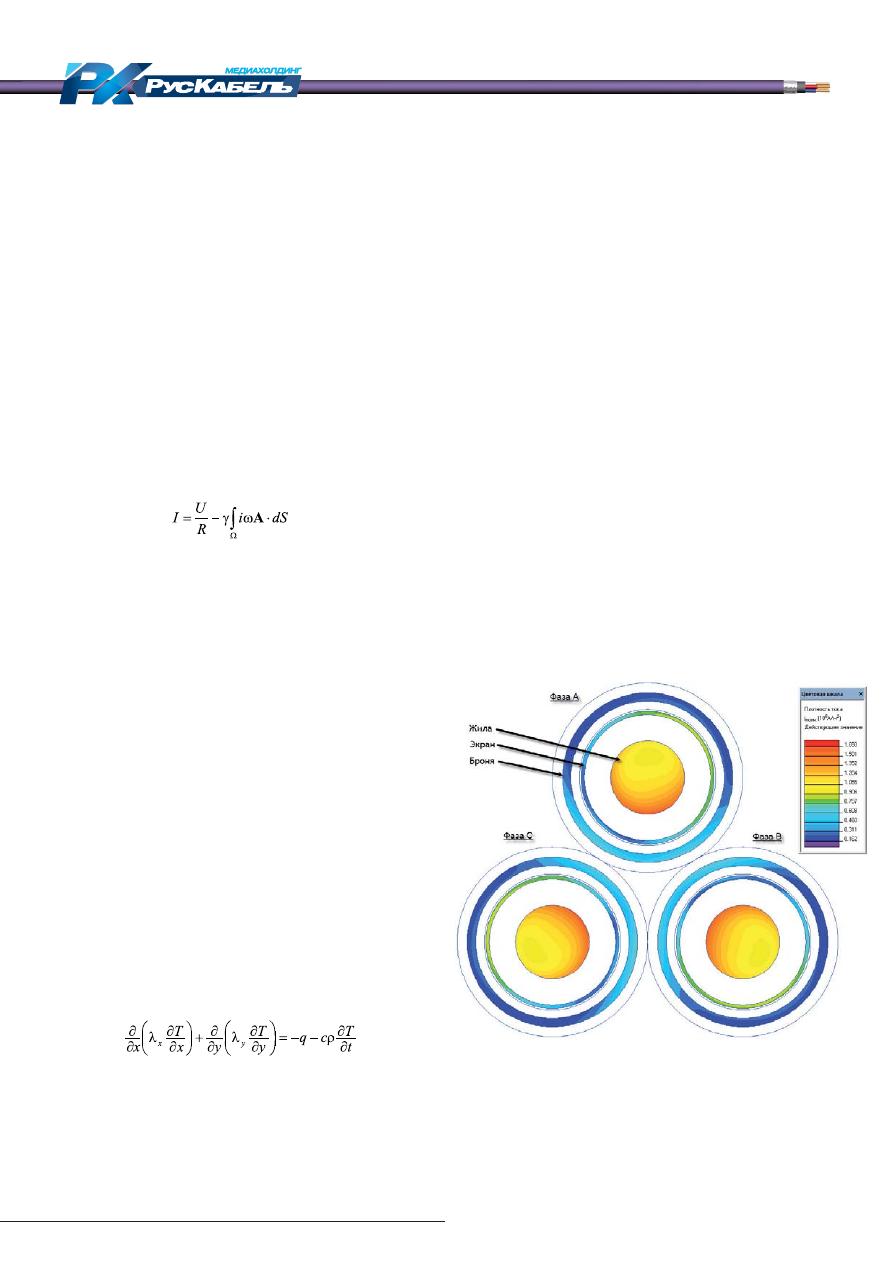
Результатом моделирования электромагнитного
поля является картина распределения плотности
тока по сечению кабелей (рис. 2):
Табл. 1. Параметры кабеля
Материал
Внешний
радиус, мм
Толщина,
мм
Площадь
сечения, мм
2
Активное сопротивление
постоянному току, Ом/м
Токопро водящая
жила
Медь
14,8
688,134
2,595•10
-5
Экран
Медь
26,75
3,3
315,8
5,655•10
-5
Броня
Алюминий
33,85
1,95
667,651
5,293•10
-5
Кабель в целом
37,7
сторонне заземлённом экране. Результаты сведены
в табл. 2.
Табл. 2. Токи и потери при прокладке
треугольником с односторонним заземлением
Ток, А
Потери
кВт/км
Напряжение
В/км
Жила
700
14,47
—
Экран
88,9
1,80
37,1
Броня
88,9
3,09
37,1
Заземление экранов с двух сторон.
Далее
рассмотрим двустороннее заземление экранов ка-
белей. Cхема соединений теперь включает в себя
сопротивления заземлителей экранов на концах ли-
нии.
Учёт сопротивления заземлителей экранов не-
обходим, поскольку оно составляет единицы Ом,
что почти на порядок превосходит активное сопро-
тивление постоян ному току километрового участка
экрана.
Численные эксперименты показывают, что вели-
чина эквивалентного сопротивления Земли слабо
влияет на распределение токов и потерь в экранах
и броне, поскольку ток через эквивалентный обрат-
ный провод не превышает 0,5% от тока экрана или
брони. В свою очередь, сопротивление заземлителя
влияет на результат существенно. Поэтому интерес-
но исследовать зависимость токов и потерь в экране
и броне от сопротивления заземления.
Влияние сопротивления заземлителя на токи
и потери в экране и броне
.
С помощью утилиты
серийных и статистических расчётов, входящей в
состав пакета ELCUT [8], проведено исследование
зависимости токов экрана и брони от сопротивления
заземлителя. Сопротивление заземлителя изменя-
лось в диапазоне 0,001—11 Ом, который с избытком
охватывает все встречающиеся на практике значе-
ния сопротивлений заземлителей экранов.
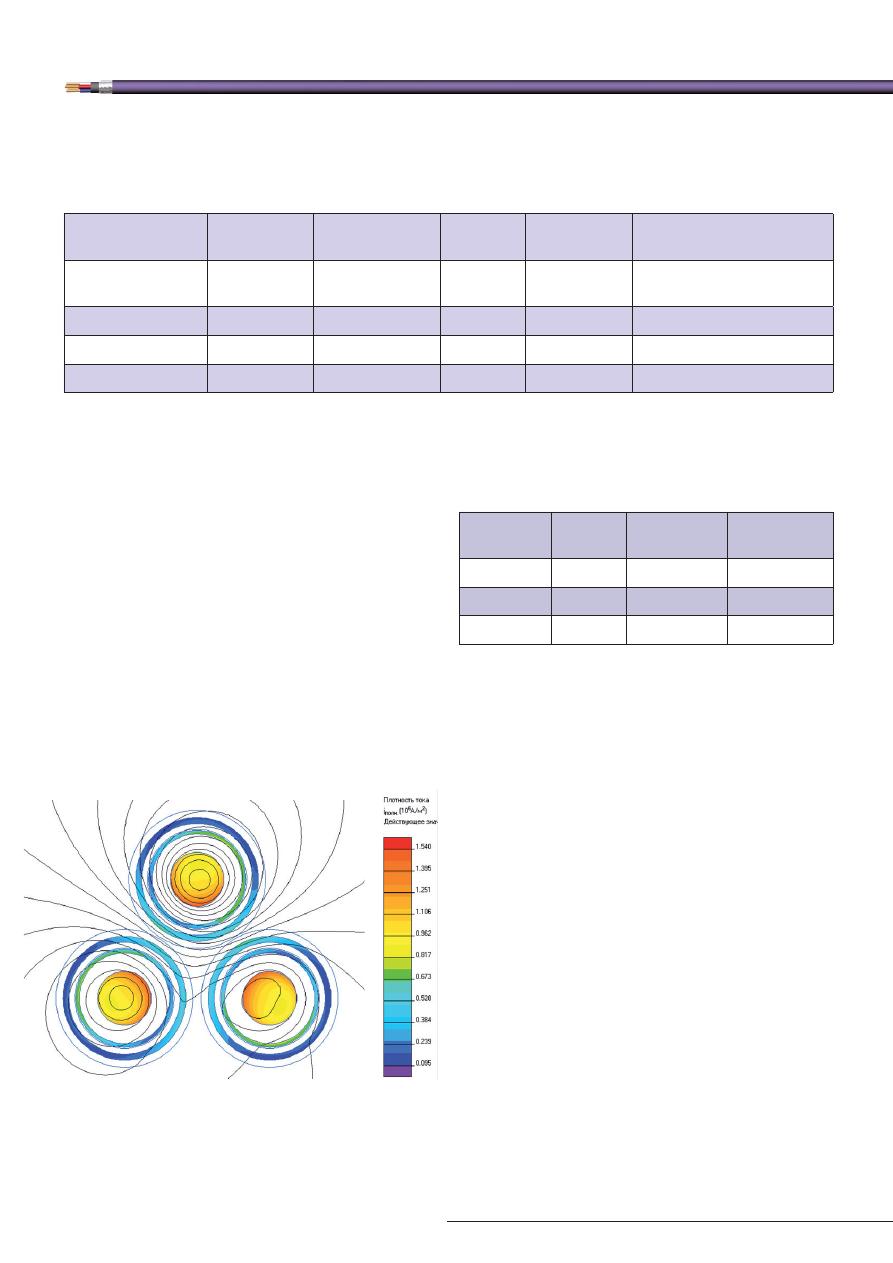
Результат численного эксперимента показан на
рис. 3 и 4.
Обратим внимание на то, что, несмотря на одно-
стороннее заземление, в экранах появляется вихре-
вой ток, а в системе экран-броня — и индуцирован-
ный циркуляционный ток. Расчёт позволяет оценить
напряжение на 1 км кабеля, индуцированное в одно-
Рис. 2. Распределение плотности тока
«КАБЕЛЬ-news», № 3, 2013, www.kabel-news.ru
35
Актуально
ÊÀÁÅËÜÍÛÅ ËÈÍÈÈ
Из рис. 3 и 4 можно сделать
вывод, что в реальном диапазоне
сопротивления заземлителя 1—
5 Ом распределение токов и по-
терь меняется слабо. Так, суммар-
ные потери в броне различаются
на концах указанного диапазона
всего на 2%, в то время как при
увеличении сопротивления за-
землителя от 0,001 до 1,0 Ом сум-
марные потери в броне и экране
уменьшаются более чем в 3 раза.
Для расчётной методики это
означает следующее:
• сопротивлением заземлителя
пренебрегать нельзя. Это об-
стоятельство обуславливает
необходимость совместного
решения уравнений электриче-
ской цепи и электромагнитного
поля;
• выбирать конкретное значение
сопротивления заземлителя в
диапазоне единиц Ом можно
достаточно свободно, посколь-
ку оно не оказывает существен-
ного влияния на мощность по-
терь в экране и броне.
ТЕПЛОВОЙ РАСЧЁТ
Знание токовой нагрузки кабе-
ля, брони и экрана позволяет рас-
считать тепловой режим кабель-
ной линии. Рассмотрим тепловое
состояние кабельной линии при
условии прокладки в земле тре-
угольником (рис. 1).
Тепловые свойства материа-
лов, использованные в расчётной
модели, приведены в табл. 3.
Источником температурного
поля для данной задачи является
распределённая по сечению токо-
проводящих жил, экранов и брони
удельная плотность джоулевых по-
терь, рассчитанная на предыду-
щем этапе. Обе задачи решаются
на одной и той же сетке конечных
элементов. Передача данных из
электро магнитного расчёта в те-
пловой происходит автома тически.
Расчётная область для темпера-
турной задачи при подземной про-
кладке кабелей показана на рис. 5.
Граничным условием для за-
дачи установившегося теплового
Рис. 3. Токи экрана и брони в зависимости от сопротивления
заземлителя, R
3
0,001
0,01
0,1
1,0
10,0
100,0
Ток экрана, действ.
Ток брони, действ.
Сумма токов брони + экрана, действ.
Ток заземлителя, действ., А
Сопротивление заземления, Ом
Т
ок, А
Рис. 4. Зависимость потерь в экране и броне от сопротивления
заземлителя, R
3
Потери брони
Потери экрана
Сумма потерь экрана + брони
0,001
0,01
0,1
1,0
10,0
100,0
Сопротивление заземления, Ом
Д
ж
оу
левы потери, Вт/км
Табл. 3. Тепловые свойства материалов
Материал
Тепло-
проводность
Вт/К•м,
Плотность
кг/м
3
Удельная
теплоемкость
Дж/кг•К
Медь 383
8930
385
Алюминий 237
2700
920
Сшитый полиэтилен
0,25
952
2000
Внутренняя оболочка
0,25
952
2000
Наружная оболочка
0,25
952
2000
Полупрово дящий слой
0,3
0,68
1500
Грунт
0,833
1500
1000
Засыпка
2,2
1800
2000
«КАБЕЛЬ-news», № 3, 2013, www.kabel-news.ru
36
Актуально
ÊÀÁÅËÜÍÛÅ ËÈÍÈÈ
режима выберем условие конвекции в воздух с по-
верхности земли. Примем температуру окружающе-
го воздуха, равную 25
º
С, а коэффициент конвекции
α
= 5 Вт/К·м
2
. Остальные границы модели описыва-
ются естественным граничным условием нулевого
нормального теплового потока.
Результатом стационарного теплового расчёта
является картина температурного поля, показанная
на рис. 6.
Расчёт показывает, что при температуре окружа-
ющего воздуха T
0
= 25
º
C максимальная температура
жилы составит T
0
= 73,1
º
C.
Итерационно повторяя электромагнитный и те-
пловой расчёты, можно подобрать токовую нагрузку
таким образом, чтобы температура жилы и экрана
вплотную приблизилась к допустимым значениям
для данного типа кабеля. Вычислительную проце-
дуру можно построить простым подбором значений
тока в заданном диапазоне либо использовать встро-
енную в ELCUT утилиту оптимизации. В последнем
случае оптимизация происходит в ограниченном ди-
апазоне одномерного пространства значений тока с
целевой функцией «максимальная близость темпе-
ратуры жилы к заданному значению». В ELCUT для
этого используется метод Брендта.
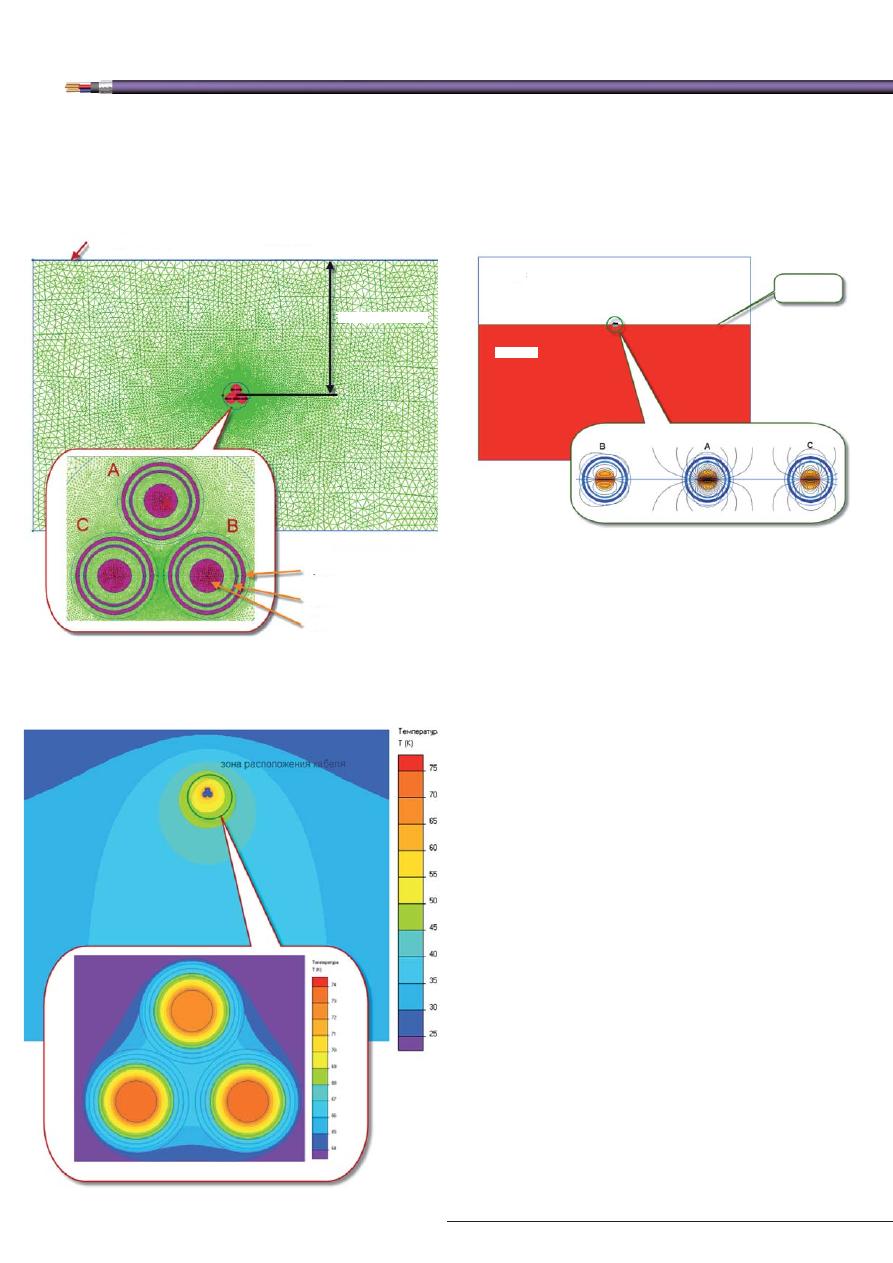
Расположение кабелей в ряд с просветом
Рассмотрим другой распространённый вариант
объединения однофазных кабелей в трёхфазную ка-
бельную группу — линейно с зазором, равным диа-
метру кабеля (рис. 7). Габариты расчётной области и
глубина залегания кабельной группы такие же, как
на рис. 5. Электромагнитный расчёт проводился при
двустороннем заземлении экранов.
Электромагнитное и температурное поля вблизи
кабелей показаны на рис. 8.
Рис. 5. Расчётная область для моделирования
температурного поля
Рис. 6. Распределение температуры вблизи
кабельной системы
(температура окружающей среды T
о
=25
о
С)
Рис. 7. Кабельная линия с линейным
расположением кабелей
воздух
земля
поверхность
земли
Броня
Тепловая изоляция
Конвекция
Глубина залегания
Экран
Жила
Поверхность земли
«КАБЕЛЬ-news», № 3, 2013, www.kabel-news.ru
37
Актуально
ÊÀÁÅËÜÍÛÅ ËÈÍÈÈ
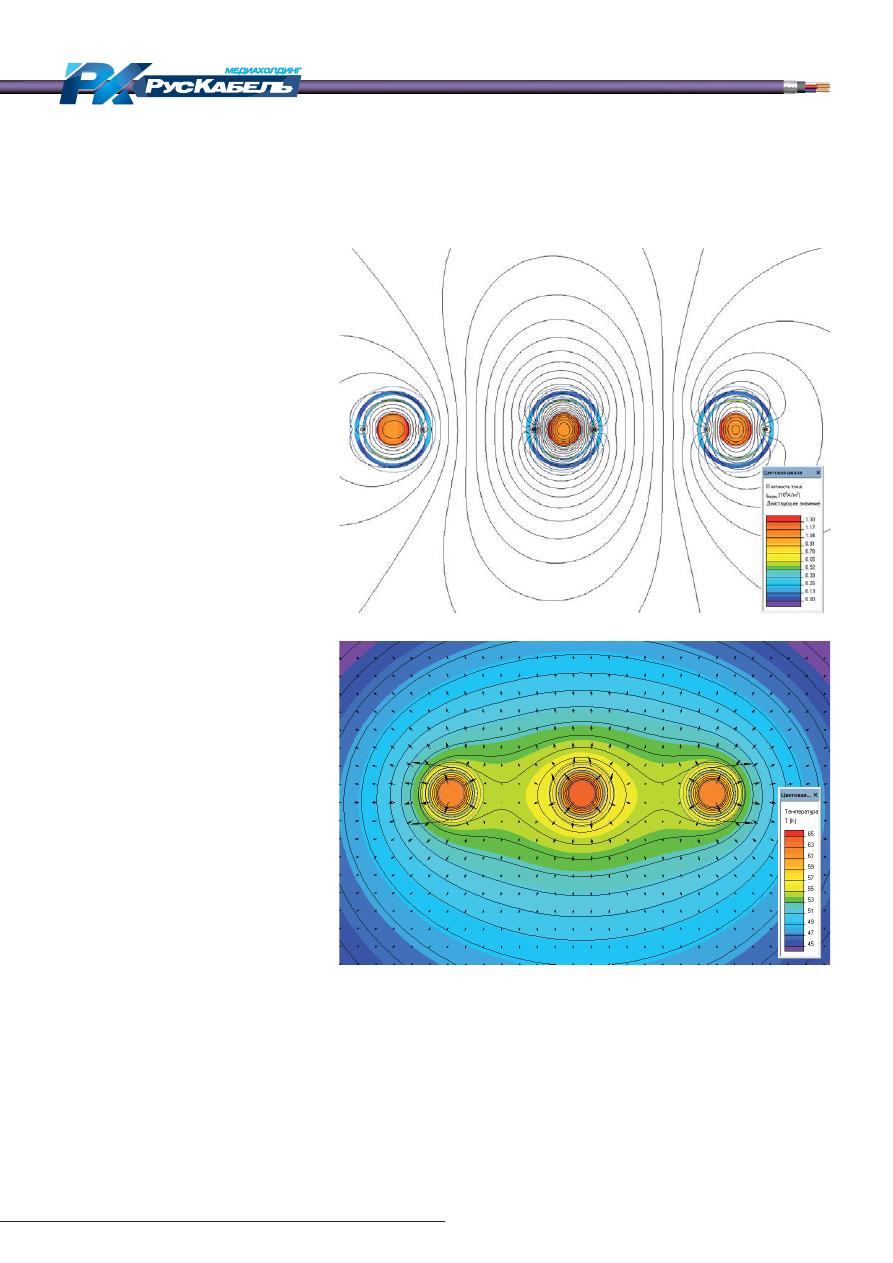
На рис. 8В изотермы проведены
через 1
о
С, стрелки показывают от-
носительную величину и направле-
ние тепловых потоков.
Сравнение с рис. 6 приводит к
выводу, что при данной глу
бине
прокладки и теплопроводности
грунта распо ложение фаз в линию
оказывается термически более вы-
годным. Это связано как с большей
индуктивной связью между экра-
нами отдельных кабелей, так и с
относительно худшими условиями
охлаждения при прокладке тре-
угольником.
ЗАКЛЮЧЕНИЕ
В работе применён метод конеч-
ных элементов для расчёта потерь
и температурного режима кабель-
ной линии. Метод позволяет учесть
электромагнитное и тепловое вза-
имное влияние кабелей друг на дру-
га, а также особенности прокладки
и наличие металлоконструкций в не-
посредственной близости.
В дополнение к предыдущим ра-
ботам на указанную тему применено
совместное решение цепно-полевой
задачи. Это позволяет точно учесть
особенности схемы заземления
и тем самым достоверно оценить
электромагнитные потери в экранах
и броне.
В данной работе исследованы
установившиеся симметричные ре-
жимы работы кабельной линии. Ме-
тод конечных элементов позволяет
проводить нестационарные расчёты
при различных аварийных режимах,
в том числе несимметричных.
ЛИТЕРАТУРА
1. Кабели электрические. Расчет
номинальной токовой нагрузки,
ГОСТ Р МЭК 60287-2009, 2009.
2.
Geoge J. Anders Rating of
Electric Power Cables: Ampacity
Computations for Transmission,
Distribution, and Industrial
Applications. — McGraw Hill
Professional, 1997, 428 c.
3. Electric cables — Calculations for
current ratings — Finite element
method. — IEC Technical Report
TR 62095. — First Edition 2003.
4. Л.А. Ковригин и др. Расчет температурных полей и токовых на-
грузок кабелей в ANSYS. «КАБЕЛЬ-news», № 4, 2009, с. 91—95.
5. Г.В. Грешняков, Г.Г. Ковалёв, С.Д. Дубицкий. К вопросу о выборе
предельно допустимых токов силовых кабелей. — «Кабели и про-
вода», № 6, 2011, с. 12—16.
6. М.В. Дмитриев, Г.А. Евдокунин. Заземление экранов однофазных
силовых кабелей высокого напряжения//Перенапряжения и на-
дёжность эксплуатации электрооборудования. СПб. 2008.
7. В.В. Титков. К оценке теплового режима трехфазной линии из
СПЭ-кабеля. «КАБЕЛЬ-news», № 10, 2009, с. 47—51.
8. ELCUT 5.10. Руководство пользователя. ООО «Тор», Санкт-
Петербург, 2012, 356 c.
Рис. 8. Распределение полей вблизи кабелей при линейной
прокладке с двусторонним заземлением экранов
A — магнитное поле
В — температурное поле
Оригинал статьи: Численный метод анализа нагрузочной способности высоковольтной кабельной системы
В данной статье представлена методика совместного расчёта электромагнитного и температурного полей трёхфазной кабельной линии с изоляцией из сшитого полиэтилена при однофазной прокладке.