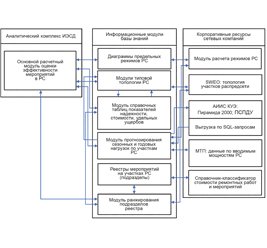
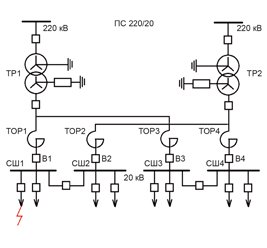
Исследуется актуальная проблема выбора узлов управления электроэнергетической системы, воздействуя на которые можно с максимальной эффективностью решать многокритериальные задачи надежного обеспечения потребителей электроэнергией необходимого качества. При этом предлагается новая методика принятия решения по выбору узлов управления электроэнергетической системы с учетом совокупности разнотипных показателей, характеризующих разные свойства этих узлов. С учетом предложенной методики рассматривается задача выбора оптимальных мест установки ветровых электростанций.
