Алгоритм диагностики состояний магистральных линий распределительных сетей в составе АСКУЭ

Page 1

Page 2

диагностика и мониторинг

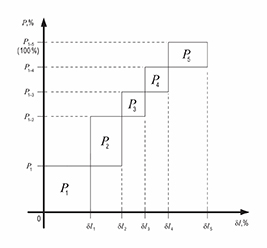
Алгоритм
диагностики состояний
магистральных линий
распределительных
сетей в составе АСКУЭ

УДК 621.316.1:658.5

Оморов

д.т.н., член-корреспондент

НАН КР, заведующий

лабораторией «Адаптивные

и интеллектуальные сис-

те мы» Института машино-

ведения и автоматики

Национальной академии наук

Кыргызской Республики

Такырбашев

к.т.н., доцент, старший

научный сотрудник лабора-

тории «Адаптивные и интел-

лектуальные системы»

Института машиноведения

и автоматики Национальной

академии наук Кыргызской

Республики

Койбагаров

Дж

аспирант лаборатории

«Адаптивные и интеллек-

туальные системы» Института

машиноведения и автоматики

Национальной академии наук

Кыргызской Республики

Жаныбаев

заместитель

генерального директора

ОАО «Северэлектро»

Ключевые

слова

распределительная сеть,

сопротивления проводов,

параметры сети, критерий

и алгоритм диагностики,

структура подсистемы

диагностики

настоящее

время

целях

автоматизации

информатизации

процессов

распределительных

электрических

сетях

(

РЭС

)

на

–

пряжением

0,4

кВ

широкое

применение

нашли

новые

техноло

–

гии

виде

автоматизированных

систем

контроля

учета

элек

–

троэнергии

(

АСКУЭ

Однако

составе

этих

информационных

систем

отсутствуют

технологии

ориентированные

на

решение

диагностических

задач

статье

предлагаются

методологиче

–

ские

алгоритмические

основы

построения

подсистемы

диа

–

гностики

состояний

проводов

магистральных

линий

РЭС

настоящее время активно внедря-

ются автоматизированные системы

контроля и учета электроэнергии

(АСКУЭ) [1] в целях комплексной ав-

томатизации распределительных электриче-

ских сетей (РЭС) напряжением 0,4 кВ, иерар-

хия которых, в основном, состоит из двух

уровней. Структура нижнего уровня включает

группу счетчиков электроэнергии (Сч), уста-

навливаемых у абонентов сети, и концентра-

тор данных (КД), который строится на базе

микропроцессорного контроллера и устанав-

ливается в трансформаторной подстанции.

Концентратор дистанционно осуществля-

ет оперативный сбор данных со счетчиков

электроэнергии в автоматическом режиме,

их хранение и после предварительной об-

работки требуемые данные передает в цен-

тральный компьютер верхнего уровня, кото-

рый располагается в диспетчерском пункте

управления. Обмен данными между струк-

турными элементами автоматизированной

системы осуществляется по каналам связи.

Основной функцией традиционных АСКУЭ

является автоматизация коммерческого уче-

та электроэнергии. В то же время в распреде-

лительных сетях наиболее важной является

задача автоматизации процессов диагности-

ки состояний ее функциональных элементов

[2–5]. При этом часть проблемы связана с ди-

агностикой состояний фазных и нейтрально-

го проводов трехфазной распредсети в усло-

виях несимметрии токов и напряжений [6–9].

Анализ показывает, что формализация и ал-

горитмизация этой задачи требует разработ-

ки соответствующей математической модели

Page 3

и метода идентификации параметров РЭС, таких

как сопротивления межабонентских участков,

в режиме реального времени. Как известно, при

эксплуатации РЭС эти параметры изменяются во

времени случайным образом в зависимости от

состояния внешней среды, что приводит к опре-

деленным трудностям при разработке моделей

физических процессов в РЭС и алгоритмов пара-

метрической идентификации. Известные методы

параметрической идентификации [10–13] в не-

достаточной степени адаптированы для их при-

менения в режиме реального времени. Один из

возможных подходов в этом направлении — это

проблема идентификации параметров распреде-

лительных сетей на основе численных методов

[14–16]. В статье предлагаются алгоритмические

основы построения подсистемы диагностики со-

стояний проводов распределительных сетей в со-

ставе АСКУЭ. При этом для идентификации теку-

щих параметров (сопротивлений) межабонентских

участков (МАУ) РЭС используется метод, изложен-

ный в [17].

ПОСТАНОВКА

ЗАДАЧИ

В качестве объекта рассматривается четырехпро-

водная РЭС напряжением 0,4 кВ, расчетная схема

которой показана на рисунке 1.

Обозначения имеют следующий смысл:

— ин-

дексные переменные (на рисунке указаны их число-

вые значения), обозначающие соответственно номе-

ра фаз А, В, С (

= 1, 3) и электрических контуров

сети (

= 1,

));

— ЭДС

-й фазы;

—

мгновенные синусоидальные напряжения и токи

соответственно на входах соответствующих фаз;

— синусоидальные мгновенные ток, на-

пряжение и сопротивление нагрузки (электроприем-

ника) с координатой (

);

— мгновенный ток

и комплексное сопротивление

-го межабонентского

участка (МАУ)

-й фазы;

— напряжения соот-

ветственно на

-м МАУ

-й фазы и нейтрального про-

вода;

— мгновенный ток и комплексное сопро-

тивление

-го участка нейтрального провода.

Далее предполагается, что выполняются следую-

щие условия:

1) трехфазная сеть является линейной системой;

2) в системе используются технические средства

для подавления высших гармонических составля-

ющих токов и напряжений в сети;

3) со счетчиков электроэнергии (Сч

), установлен-

ных у абонентов сети и в трансформаторной под-

станции, в базу данных АСКУЭ по каналам связи

в дискретные моменты времени

∈

[





+ 1

] с ша-

гом дискретизации









+ 1

–



(



= 1, 2, …) по-

ступают следующие данные:

– действующие значения токов

и напряжений

на входах фаз и нагрузках сети;

– коэффициенты мощности

cos



, опреде-

ляемые фазовыми сдвигами



между соот-

ветствующими напряжениями

и токами

(

= 1, 3,

= 0,

Задача состоит в определении алгоритма диа-

гностики и структуры подсистемы диагностики со-

стояний МАУ распределительной сети в составе

АСКУЭ.

Решение сформулированной задачи включает

следующие основные этапы:

– идентификация параметров (сопротивлений)

МАУ;

– формулировка критерия диагностики;

– алгоритмизация решения задачи диагностики;

– определение структуры программного комплекса

подсистемы диагностики.

Рис

. 1.

Расчетная

схема

трехфазной

сети

№

3 (66) 2021

Page 4

ИДЕНТИФИКАЦИЯ

ПАРАМЕТРОВ

МАУ

Исходные данные для решения сформулирован-

ной задачи представим в виде следующих матриц

и векторов:

…

;

…

;

…

;

…

= [

];

= [

];

= [

Как известно, в традиционных АСКУЭ межабо-

нентские комплексные токи

и напряжения

не идентифицируются и не контролируются. В то

же время в АСКУЭ имеется возможность их опре-

деления по данным со счетчиков электроэнергии

системы, что позволяет решать ряд важных функ-

циональных задач, таких как идентификация не-

контролируемого потребления электроэнергии

[18–20] и симметрирования распредсети [8, 21–23].

При этом мгновенные синусоидальные токи

напряжения

на соответствующих нагрузках и их

сопротивления

в установившемся режиме можно

представить в комплексной форме [24]:

(





)

(1)

(





)

(2)

= 1,

= 1, 3,

где символы «в» и «м» обозначают вещественные

и мнимые части соответствующих комплексных

переменных;

— модули этих переменных.

При этом





–





= 2(

– 1)



/3, где





—

приращения фазовых сдвигов относительно их номи-

нальных значений



, обусловленные несимметрией

токов и напряжений в сети.

В случае, когда построена модель нагрузок в уста-

новившемся режиме в форме (1) и (2), межабонент-

ские токи и напряжения можно оценить на основе

известных законов электротехники [24] (рисунок 1),

то есть:



(

) =

(





)

(3)

= 1,

= 1, 3,

(4)

где



— действующее значение и приращение

фазового сдвига межабонентского комплексного

тока

соответственно.

Далее будем считать, что на основе метода, пред-

ложенного в [17], построена модель распредсети

в комплексной форме (1)–(4) и на ее основе иден-

тифицированы текущие значения сопротивлений ме-

жабонентских участков фазных проводов

и ней-

трального провода

трехфазной сети.

КРИТЕРИЙ

ДИАГНОСТИКИ

Введем векторы

, составленные из теку-

щих значений параметров межабонентских участков

фазных и нейтрального проводов в момент времени

∈



= [

, …,

= [

, …,

= [

, …,

= [

, …,

На основе указанных векторов составляем мат-

рицу

…

Можно отметить, что элементы матрицы

нахо-

дятся в результате решения задачи идентификации

параметров распредсети.

Далее будем предполагать, что по паспортным

данным предварительно определены и записаны

в базе данных концентратора (КД) базовая матрица

*, составленная соответственно из номинальных

значений параметров сети



Для диагностики состояний межабонентских

участков магистральной линии используются дан-

ные идентификации текущих параметров РЭС, пред-

ставленные матрицей

и компоненты базовой ма-

трицы

…

* =

…

В общем случае для оценки уровня износа элек-

трических линий межабонентских участков сети

можно поступить следующим образом. Вначале вы-

числяются относительные отклонения текущих зна-

чений параметров сети от их номинальных значений:









= (|



–



|) /



= 1,



= 0, 3,

(5)

где



— индексная переменная, которая обознача-

ет номера нулевого и фазных проводов трехфазной

сети.

Как известно, технические потери электроэнергии

в соответствующих участках сети увеличиваются,

если найденные оценки





превышают их крити-

ческие значения. Поэтому критерием нормального

состояния электрических линий РЭС можно принять

выполнение следующих условий:









≤





max

= 1,



= 0, 3,

(6)

где





max

— максимально допустимые относительные

уровни износа соответствующих линий электроснаб-

жения.

ДИАГНОСТИКА

И МОНИТОРИНГ

Page 5

АЛГОРИТМИЗАЦИЯ

РЕШЕНИЯ

ЗАДАЧИ

ДИАГНОСТИКИ

В целях алгоритмизации решения задачи диагно-

стики состояния проводов межабонентских участков

магистральной линии распредсети введем в рассмо-

трение матрицу

= {



}

×4

, имеющую такую же раз-

мерность, как и матрица

, то есть



= 0, 3,

= 1,

При этом первая строка соответствует состояниям

межабонентских участков (МАУ) нейтрального (нуле-

вого) провода, а остальные три строки соответствуют

состояниям МАУ трех фазовых проводов сети. Ком-

поненты этой матрицы



определим по следующе-

му правилу:

0, если







≤







= 1, если









= 0, 3,

= 1,

Рис

. 3.

Структура

программного

комплекса

под

системы

диагностики

состояний

проводов

МАУ

распредсети

Формирование матрицы

осу-

ществляется на основе критериаль-

ных условий (6), то есть если со-

стояние соответствующего провода

с координатой (



) отвечает задан-

ным требованиям, то





= 0, в про-

тивном случае





= 1.

Алгоритм диагностики состояний

МАУ трехфазной сети, полученный

на основе критериальных усло вий

(6), приведен на рисунке 2.

СТРУКТУРА

ПРОГРАММНОГО

ОБЕСПЕЧЕНИЯ

ПОД

–

СИСТЕМЫ

ДИАГНОСТИКИ

Обобщенная структура программ-

ного комплекса подсистемы диа-

гностики, приведенная на рисунке 3,

включает следующие программные

модули:

– модуль формирования исходных

данных (МФИД);

– модуль идентификации текущих

параметров (сопротивлений) МАУ

сети (МИП);

– модуль формирования базовых

значений параметров (МФБП);

– модуль диагностики (МД).

В процессе функционирования

распредсети путем опроса счетчиков

АСКУЭ соответствующие данные по-

ступают в базу данных концентрато-

ра (КД). На их основе программный

модуль МФИД формирует матрицу

и векторы

Далее эти данные поступают

в модуль МИП, который, в свою оче-

редь, осуществляет идентификацию

матрицы

В программном модуле МФБП

осуществляется вычисление эле-

ментов базовой матрицы

*. Далее

на основе компонентов матрицы

* в программном модуле МД на

Рис

. 2.

Алгоритм

диагностики

состояний

межабонентских

участков

магистральной

ли

–

нии

трехфазной

сети

Начало

Конец

Программный комплекс диагностики состояний МАУ

МФИД

Счетчики

АСКУЭ

МД

МФБП

МИП

Решение задачи идентификации

параметров (сопротивлений) сети

и формирование матрицы

Запись в базу данных концен-

тратора (КД) АСКУЭ элементов

матрицы



:= 0

(формирование

элементов

)

Диагностика состояний

МАУ магистральной линии сети

на основе анализа матрицы

)



:= 1

(формирование

элементов

)

Вычисление





по формуле (5)

Да

Нет



:= 0



+ 1



> 3?

:= 1

+ 1







≤





№

3 (66) 2021

Page 6

ДИАГНОСТИКА

И МОНИТОРИНГ

основе критерия (6) и анализа матрицы

осущест-

вляется диагностика состояний проводов МАУ рас-

пределительной сети.

ЗАКЛЮЧЕНИЕ

Предложены алгоритмические основы построения

подсистемы диагностики состояний фазных и ней-

трального проводов трехфазной распределительной

сети напряжением 0,4 кВ, функционирующей в усло-

виях несимметрии токов и напряжений. Исходными

данными служат измерительные данные АСКУЭ, по-

лученные с группы счетчиков электроэнергии, уста-

новленных у абонентов сети и в трансформаторной

подстанции. Вычислительная процедура метода ба-

зируется на идее сравнения текущих значений со-

противлений (параметров) межабонентских участков

сети с их базовыми значениями, полученными на

основе паспортных данных проводов магистраль-

ной линии, которые предварительно определяются

и записываются в базу данных автоматизированной

системы. В целях диагностики предложен критерий,

определяющий критический уровень износа прово-

дов распредсети. На его основе разработан алго-

ритм диагностики состояний проводов трехфазной

распределительной сети, который ориентирован для

создания диагностической подсистемы в составе

традиционной АСКУЭ, что дает возможность распре-

делительным компаниям принимать оперативные

меры по поддержанию электрических проводов рас-

предсети в требуемом состоянии.

ЛИТЕРАТУРА

1. Ожегов А.Н. Системы АСКУЭ. Киров:

ВятГУ, 2006. 102 с.

2. Киншт Н.В., Петрунько Н.Н. Диагно-

стика электрических цепей и систем.

Владивосток: Дальнаука, 2013. 242 c.

3. Ершов А.М., Филатов О.В., Молоток

А.В. и др. Система защиты элек-

трической сети напряжением 380 В

от обрывов воздушной линии //

Электрические станции, 2016, № 5.

С. 28–33.

4. Фардиев И.Ш., Минуллин Р.Г., За-

камский Е.В., Андреев В.В., Губаев

Д.Ф. Диагностика воздушных линий

распределительных электрических

сетей // Известия высших учебных

заведений. Проблемы энергетики,

2004, № 7–8. С. 41–49.

5. Клочков А.Н. Устройство для обнару-

жения трехфазных сетей с обрывом

фазного провода // Вестник Красно-

ярского государственного аграрного

университета, 2011, № 1. С. 221–223.

6. Войтов О.Н., Мантров В.А., Семе-

нова Л.В. Анализ несимметричных

режимов электроэнергетических

сис тем и управление ими // Электри-

чество, 1999, № 10. С. 2–18.

7. Пономаренко О.И., Холиддинов И.Х.

Влияние несимметричных режимов

на потери мощности в электриче-

ских сетях распределенных систем

электроснабжения // Энергетик,

2015, № 12. С. 6–8.

8. Косоухов Ф.Д., Васильев Н.В., Фи-

липпов А.О. Снижение потерь от не-

симметрии токов и повышение каче-

ства электрической энергии в сетях

0,38 кВ с коммунально-бытовыми

нагрузками // Электротехника, 2014,

№ 6. С. 8–12.

9. Оморов Т.Т. Оценка влияния не-

симметрии токов и напряжений на

потери электроэнергии в распреде-

лительной сети с использованием

АСКУЭ // Электричество, 2017, № 9.

С. 17–23.

10. Степанов А.С., Степанов С.А., Ко-

стюкова С.С. Идентификация па-

раметров моделей элементов элек-

трических сетей на основе теоремы

Теллегена // Электротехника, 2016,

№ 7. C. 8–11.

11. Будникова И.К., Белашова Е.С.

Компьютерное моделирование па-

раметров распределительной элек-

трической сети // Известия высших

учебных заведений. Проблемы

энергетики, 2014, № 9–10. С. 75–81.

12. Ягуп В.Г., Ягуп Е.В. Идентифика-

ция параметров трехфазной ли-

нейной нагрузки для компенсации

реактивной мощности с помощью

поисковой оптимизации // Тех-

нiчна електродинамiка, 2019, № 3.

С. 67–73.

13. Шелюг С.Н. Методы адаптивной

идентификации параметров схемы

замещения элементов электриче-

ской сети: дис. канд. техн. наук. Ека-

теринбург, 2000. 181 с.

14. Бахвалов Н.С., Жидков Н.П., Ко-

бельков Г.М. Численные методы. М.:

Лаб. базовых знаний, 2002. 632 с.

15. Оморов Т.Т., Кожекова Г.А. Синтез

системы управления синхронным

генератором // Приборы и системы.

Управление, контроль, диагностика,

2011, № 1. С. 5–9.

16. Оморов Т.Т., Кожекова Г.А. Синтез

законов управления взаимосвязан-

ными электроприводами // Приборы

и системы. Управление, контроль,

диагностика, 2009, № 10. С. 10–13.

17. Оморов Т.Т., Закиряев К.Э., Осмо-

нова Р.Ч., Такырбашев Б.К. Метод

идентификации параметров трех-

фазной распределительной сети на

основе решения оптимизационной

задачи // Приборы и системы. Управ-

ление, контроль, диагностика, 2020,

№ 4. С. 1–9.

18. Сапронов А.А., Кужеков С.Л., Тынян-

ский В.Г. Оперативное выявление

неконтролируемого

потребления

электроэнергии в электрических се-

тях напряжением до 1 кВ // Известия

вузов. Электромеханика, 2004, № 1.

С. 55–58.

19. Оморов Т.Т. К проблеме локализа-

ции несанкционированного отбора

электроэнергии в распределитель-

ных сетях в составе АСКУЭ // Прибо-

ры и системы. Управление, контроль,

диагностика, 2017, № 7. С. 27–32.

20. Данилов М.И., Романенко И.Г. Ме-

тод выявления мест неконтролиру-

емого потребления электроэнергии

в электрических сетях 0,4 кВ // Из-

вестия высших учебных заведений.

Электромеханика, 2019, т. 62, № 4.

С. 90–96.

21. Киселев М.Г., Лепанов М.Г. Симме-

трирование токов в сетях электро-

снабжения силовым электрическим

регулятором неактивной мощно-

сти // Электротехника, 2018, № 11.

С. 63–70.

22. Наумов И.В., Иванов Д.А., Подъячих

С.В., Гантулга Дамдинсурэн. Симме-

трирующее устройство для трехфаз-

ных сетей с нулевым проводом. Пат.

№ 2490768 РФ; опубл. 20.08.2013,

Бюл. № 23.

23. Оморов Т.Т. Симметрирование рас-

пределенной электрической сети

методом цифрового регулирования //

Мехатроника, автоматизация, управ-

ление, 2018, т. 19, № 3. С. 194–200.

24. Демирчян К.С., Нейман Л.Р., Коров-

кин А.В. Теоретические основы элек-

тротехники. Т.1. СПб.: Питер, 2009.

512 c.

REFERENCES

1. Ozhegov A.N. Automated meter read-

ing and control systems. Kirov, VyatGU

Publ., 2006. 102 p.

2. Kinsht N.V., Petrun’ko N.N. Diagno-

sis of electrical circuits and systems.

Vladivostok, Dal’nauka Publ., 2013.

242 p.

3. Ershov A.M., Filatov O.V., Molotok A.V.

and others. Overhead line break pro-

tection system for a 380 kV electrical

network // Electric power stations, 2016,

no. 5, pp. 28-33.

4. Fardiyev I.Sh., Minullin R.G., Zakams-

kiy E.V., Andreyev V.V., Gubayev D.F.

Distribution network overhead line diag-

Page 7

nosis // News of higher educational es-

tablishments. Issues of power industry,

2004, no. 7-8, pp. 41-49.

5. Klochkov A.N. Detector of a three-

phase network with broken wire // News

of Krasnoyarsk State Agrarian Univer-

sity, 2011, no. 1, pp. 221-223.

6. Voytov O.N., Mantrov V.A., Semenova

L.V. Study of asymmetric operating

modes of electric power systems and

their control // Electricity, 1999, no. 10,

pp. 2-18.

7. Ponomarenko O.I., Kholiddinov I.Kh.

Asymmetric operating mode impact

on power losses in electrical networks

of distribution power systems // Power

engineer, 2015, no. 12, pp. 6-8.

8. Kosoukhov F.D., Vasiliyev N.V., Filip-

pov A.O. Reduction of losses caused

by current asymmetry and power qual-

ity improvement in 0,38 kV residential

networks // Electric engineering, 2014,

no. 6, pp. 8-12.

9. Omorov T.T. Assessment of current

and voltage asymmetry impact on

power losses in distribution networks

by means of automated meter reading

and control system // Electricity, 2017,

no. 9, pp. 17-23.

10. Stepanov A.S., Stepanov S.A., Kostyu-

kova S.S. Identiﬁ cation of model pa-

rameters of electrical network com-

ponents based on Tellegen theorema

// Electric engineering, 2016, no. 7,

pp. 8-11.

11. Budnikova I.K., Belashova E.S. Com-

puter simulation of distribution network

parameters // News of higher educa-

tional establishments. Issues of power

industry, 2014, no. 9-10, pp. 75-81.

12. Yagup V.G., Yagup E.V. Parameter

identiﬁ cation of a three-phase line

load aimed for reactive power com-

pensation via search optimization //

Технiчна електродинамiка, 2019,

no. 3, pp. 67-73.

13. Shelyug S.N. Methods of adaptive pa-

rameter identiﬁ cation of the electrical

network component replacement dia-

gram: PhD thesis in Engineering Sci-

ence. Ekaterinburg, 2000. 181 p.

14. Bakhvalov N.S., Zhidkov N.P., Ko-

bel’kov G.M. Numerical methods. Mos-

cow, Basics laboratory, 2002. 632 p.

15. Omorov T.T., Kozhekova G.A. Syn-

chronous generator control system de-

sign // Instruments and systems. Con-

trol, monitoring, diagnosis, 2011, no. 1,

pp. 5-9.

16. Omorov T.T., Kozhekova G.A. Synthe-

sis of interconnected wire control laws

// Instruments and systems. Control,

monitoring, diagnosis, 2009, no. 10,

pp. 10-13.

17. Omorov T.T., Zakiryayev K.E., Osmon-

ova R.Ch., Takyrbashev B.K. Method

of parameter identiﬁ cation of a three-

phase distribution network by means

of optimization // Instruments and sys-

tems. Control, monitoring, diagnosis,

2020, no. 4, pp. 1-9.

18. Sapronov A.A., Kuzhekov S.L., Tyn-

yanskiy V.G. Online detection of un-

controlled power consumption in elec-

trical networks for under 1 kV // News

of universities. Electromechanics,

2004, no. 1, pp. 55-58.

19. Omorov T.T. To location of unauthorized

power outlets in distribution networks

within the automated meter reading and

control system // Pribory i sistemy. Up-

ravleniye, kontrol’, diagnostika [Instru-

ments and systems. Control, monitor-

ing, diagnosis], 2017, no. 7, pp. 27-32.

20. Danilov M.I., Romanenko I.G. Method

of detecting uncontrolled power con-

sumption locations in 0,4 kV electrical

networks // Izvestiya vysshykh ucheb-

nykh zavedeniy. Elektromekhanika

[News of higher educational estab-

lishments. Electromechanics], 2019,

vol. 62, no. 4, pp. 90-96.

21. Kiselev M.G., Lepanov M.G. Current

balancing in power supply networks

by means of reactive power regulator

// Electric engineering, 2018, no. 11,

pp. 63-70. (In Russian)

22. Naumov I.V., Ivanov D.A., Pod’ya-

chikh S.V., Gantulga Damdinsuren. Bal-

ancing device for three-phase networks

with zero wire. Patent no. 2490768 RF;

published 20.08.2013, bull. no. 23.

23. Omorov T.T. Distribution network bal-

ancing by means of digital control //

Mekhatronika, avtomatizatsiya, uprav-

leniye [Mechatronics, automation, con-

trol], 2018, vol. 19, no. 3, pp. 194-200.

24. Demirchyan K.S., Neyman L.R., Koro-

vkin A.V. Theoretical basics of electrical

engineering. Volume 1. Saint-Peters-

burg, Piter Publ., 2009. 512 p.

ООО «ЕГЕ-ЭНЕРГАН»

197183, Санкт-Петербург, Липовая аллея, д. 9, БЦ «Приморский»

Тел.: (812) 373-90-30, 373-90-17,

e-mail: info@energan.ru

На прав

ах рек

ламы

www.ege-energan.ru

Стандартные
резисторы NER

ОО

«Е

ЕГЕ

ГЕ

-Э

НЕ

РГ

АН

197183, С

Тел.: (

(резистор
и трансформатор вывода
нейтрали в одном шкафу)

Комбинированные
резисторы NERС

•  Номинальное напряжение сети: 6, 10, 15, 20, 24, 35 кВ
•  Номинальный ток: от 1 до 2000 А
•  Номинальное сопротивление: от 1 до 10 000 Ом
•  Время протекания номинального тока:

от 5 с до длительного

• Материал рабочего элемента резистора: металл

(сплав никель-хром-вольфрам-молибден)

• Трансформатор вывода нейтрали с сухой изоляцией
• Встроенные трансформаторы тока (количество ТТ

и число вторичных обмоток — по заказу)

• Интеллектуальный блок контроля нагрева резистора

(по заказу)

•  Степень защиты шкафа: от IP23 до IP55
•  Материал шкафа: нержавеющая сталь
•  Охлаждение: естественное, воздушное
•  Исполнение: для наружной/внутренней установки
•  Сейсмостойкость: до 9 баллов по шкале MSK-64
•  Диапазон рабочих температур: от –60 до +45°С
•  Экспертное заключение ПАО «Россети»

дугогасящие реакторы, резисторы заземления нейтрали,
трансформаторы вывода нейтральной точки

Продукция поставляется

по программам импортозамещения

№

3 (66) 2021

Оригинал статьи: Алгоритм диагностики состояний магистральных линий распределительных сетей в составе АСКУЭ

Ключевые слова: распределительная сеть, сопротивления проводов, параметры сети, критерий и алгоритм диагностики, структура подсистемы диагностики

Читать онлайн

В настоящее время в целях автоматизации и информатизации процессов в распределительных электрических сетях (РЭС) напряжением 0,4 кВ широкое применение нашли новые технологии в виде автоматизированных систем контроля и учета электроэнергии (АСКУЭ). Однако в составе этих информационных систем отсутствуют технологии, ориентированные на решение диагностических задач. В статье предлагаются методологические и алгоритмические основы построения подсистемы диагностики состояний проводов магистральных линий РЭС.